1 Introduction

Islands usually have relatively abundant renewable resources (such as solar, wind and tide energy, etc.), but still most of them are powered by diesel engines [1, 2], which has poor supply reliability and can cause noise and atmospheric pollutants. Microgrid is a flexible and efficient renewable energy utilization method and has advantages in guaranteeing the security of the power supply, improving the renewable energy utilization rate and the power quality. Therefore, renewable energy sources in the microgrid are considered as the best choice to solve small island energy supply problems [2, 3].

Due to the randomness and intermittent nature of renewable energy [4], as well as the load fluctuation, energy storage systems are required to be configured in an isolated microgrid. Most of the existing researches employ battery energy storage in the microgrid [5]. However, battery storage has the disadvantages of short life, high cost, environmental friendliness and difficult maintenance. By contrast, because of their high reliability, friendly environment and low cost, pumped storage is the main energy storage form in a large power grid. In addition, the joint operation of a pumped storage power station and renewable energy station has been proved to be helpful in reducing the phenomenon of discard wind and solar [6]. In [7,8,9,10,11,12], the application of a small or micro pumped storage system in an isolated microgrid is studied. A seawater desalination system powered by renewable energy and a pumped storage system are designed in [7]. In [8], the feasibility of the technology of a island wind/solar/pumped storage system is analyzed, and the results show that it is feasible to use a small seawater pumped storage system. Software for a hybrid system consisting of wind/solar/battery/pumped storage/seawater desalination is developed in [9]. Power sources capacity and reservoir capacity of a microgrid with a renewable energy and pumped storage system is optimized by using a genetic algorithm [10, 11].

Many islands have abundant seawater pumped storage resources. According to the analysis of Hainan, et al. seawater pumped storage resources, these three coastal provinces have 81 sites that are suited for the construction of a seawater pumped storage system, 30 of which are islands [13]. It is necessary to select an island energy storage form through technical and economic analysis. In [12], the life cycle cost of a microgrid with different energy storage schemes (including battery storage, seawater pumped storage and hybrid energy storage systems) is analyzed under the condition of a given island microgrid with the necessary energy storage requirements. The results show that, in most cases, the cost of the pumped storage scheme is lower than that of the battery storage scheme, and the cost difference is related to factors such as the demand for energy storage and the rate of return on the investment of the assets.

According to statistics in [14], about 60% of the total residential load is controllable load. With the development of a smart home, most of the household appliances will become controllable demand response resources. Therefore making full use of the demand response has practical significance. The demand response is proved to have features of smoothing power fluctuations [15,16,17,18], reducing operational costs [16, 17, 19], reducing pollutant emissions [16, 25] and improving the utilization of renewable energy [19]. To the best of our knowledge, there are few researches concentrated on microgrid configuration considering demand response. In [20, 21], island microgrid sizing optimization considering demand response is studied, but the demand response resource is the fixed seawater desalination load without considering different demand response participation degrees. The demand response participation degree (DRPD) [15, 18] is closely related to the interests of the demand response, but many of the current researches ignored the impact of the DRPD. For an island microgrid with the residential load as the main load, the demand response resources are primarily the deferrable load of the household appliances.

In this paper, the configuration refers to the sizing of all major devices in an island microgrid including the number of wind turbines, number of solar arrays, pump unit capacity, turbine unit capacity and reservoir volume. And the optimal configuration model is established for the island microgrid with a solar–wind-pumped storage system considering demand response, which is solved by using a particle swarm optimization algorithm. Compared with the existing island microgrid configuration researches, the main contributions of this paper include: ① The scheme of pumped storage is adopted, and the quantity of the power source and the capacity of the energy storage system are optimized. ② The effect of demand response on capacity configuration is considered. ③ The microgrid capacity configuration of the battery storage scheme and pumped storage scheme is compared. ④ The effects of demand response participation degree, the household number, the demand response compensation cost and the water head of the pumped storage system on the microgrid configuration are analyzed.

The rest of this paper is organized as follows. Microgrid components and modeling including PV, wind turbine and pumped storage systems are explained in Section 2. Section 3 presents the optimal configuration model considering demand response. A case study and its related analysis are presented in Section 4. Finally, the conclusions are given in Section 5.

2 Main components of an island microgrid

2.1 Island microgrid structure with pumped storage system

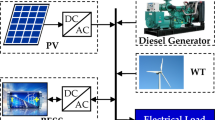
A typical structure of an island microgrid with a pumped storage system is shown in Fig. 1. Power sources consist of a photovoltaic array and wind turbine. The pumped storage system is used to store surplus power during the day time and generate power during the night time. The island load is composed of the non-deferrable load and the deferrable load. The frequency limitation problem of an island microgrid is attracting the attention of researchers. As the double-penstock system helps to regulate voltage and maintain a stable frequency with suitable control strategies [8] and as there is no suitable generator unit for a micro reversible pumped storage system, this paper adopts the double-penstock seawater pumped storage system rather than the single-penstock pumped storage system [12].

Fig. 1
figure 1

Structure of island microgrid

Full size image

2.2 Wind turbine

The output power of the wind turbine is related to the wind speed, and it can be calculated by [22]:

$$ P_{{\text{WT} }} (t) = \left\{ {\begin{array}{*{20}l} 0 \hfill & {V(t) < V_{{ci}} } \hfill \\ {\frac{{N_{{{\text{WT}}}} \left( {V^{3} (t) - V_{{ci}}^{3} } \right)P_{\text{r} } }}{{(V_{r}^{3} - V_{{ci}}^{3} )}}} \hfill & {V_{{\text{ci} }} < V(t) < V_{\text{r} } } \hfill \\ {N_{{{\text{WT}}}} P_{r} } \hfill & {V_{r} < V(t) < V_{{co}} } \hfill \\ 0 \hfill & {V(t) > V_{{co}} } \hfill \\ \end{array} } \right. $$
(1)

where \( N_{\text{WT}} \) is the number of wind turbines; \( P_{\text{r} } \) is the rated power of the wind turbine (kW); \( V(t) \) is the local wind speed (m/s); \( V_{ci} \)is the cut-in wind speed (m/s); \( V_{\text{r}} \) is the rated wind speed (m/s); \( V_{co} \) is the cut-out wind speed (m/s).

2.3 PV array

The fundamental component of a PV array is the solar cell, which can be connected in series and/or parallel to form PV modules. A typical module will have 24/72 cells connected in series. The PV modules are then combined in series and parallel to form PV arrays. Photovoltaic output power is affected by the solar light intensity, working temperature and the cleanliness of the photovoltaic panels. The output power of the PV array can be expressed as:

$$ P_{\text{PV}} (t) = N_{\text{PV}} \eta_{\text{PV}} P_{\text{STC}} \frac{{I_{\text{rad}} (t)}}{{I_{\text{STC}} }} $$
(2)

where \( N_{\text{PV}} \) is the number of photovoltaic panels; \( I_{\text{rad}} (t) \) is the ambient solar intensity; \( I_{\text{STC}} \) is the solar intensity under standard test conditions; \( P_{\text{STC}} \) is the photovoltaic panels power under standard test conditions; \( \eta_{\text{PV}} \) is the system efficiency that relates to the working temperature and cleanliness of panel.

2.4 Pumped storage system

Although the island freshwater resources are not abundant, it can be very convenient to store gravitational potential energy by elevating the seawater. A seawater pumped storage system utilizes the sea as a lower reservoir, and we need to build a tank as the upper reservoir to reduce the cost of the pumped storage system. The volume of water remaining in the upper reservoir can be determined as:

$$ W(t + 1) = W(t) + [Q_{\text{P}} (t) - Q_{\text{T}} (t)]\Delta t $$
(3)
$$ {\kern 1pt} Q_{\text{P}} (t) = \frac{{3600 \cdot 1000\eta_{\text{P}} \eta_{\text{WP}} P_{\text{P}} (t)}}{\rho gh} = K_{\text{P}} P_{\text{P}} (t) $$
(4)
$$ Q_{\text{T}} (t) = \frac{{3600 \cdot 1000P_{\text{T}} (t)}}{{\eta_{\text{T}} \eta_{\text{WP}} \rho gh}} = K_{\text{T}} P_{\text{T}} (t) $$
(5)

Where \( W(t) \) is the volume of residual water in the upper reservoir at the end of the tth time interval (m3); \( Q_{\text{P}} (t) \) is the pumping speed (m3/h); \( Q_{\text{T}} (t) \) is the discharge water speed (m3/h); \( \Delta t \) is the time interval (h); \( \eta_{\text{WP}} \) is the pipeline conveyance efficiency; \( \eta_{\text{P}} \) is the pump efficiency; \( P_{\text{P}} (t) \) is the pumping power (kW); \( \eta_{\text{T}} \) is the efficiency of generator unit; \( P_{\text{T}} (t) \) is the power of generator unit (kW); \( \rho \) is the density of water (1000 kg/m3); \( g \) is the gravitational acceleration (9.8 m/s2); \( h \) is the water head (m); KP and KT are respectively the ratios of flow rate to the pumping power and the generation power (m3/kWh).

Reservoir capacity constraint:

$$ W^{\hbox{min} } \le W(t) \le W^{\text{max}} $$
(6)

Working state constraint of pumping and generating unit:

$$ U_{\text{P}} (t) + U_{\text{T}} (t) \le 1 $$
(7)

Power constraints of pumping and generating units:

$$ U_{\text{P}} (t)P_{\text{P}}^{\hbox{min} } \le P_{\text{P}} (t) \le U_{\text{P}} (t)P_{\text{P}}^{\hbox{max} } $$
(8)
$$ U_{\text{T}} (t)P_{\text{T}}^{\hbox{min} } \le P_{\text{T}} (t) \le U_{\text{T}} (t)P_{\text{T}}^{\hbox{max} } $$
(9)

where \( W^{\hbox{max} } \) and \( W^{\hbox{min} } \) are respectively the maximum and minimum storage capacity of the reservoir; \( U_{\text{P}} (t) \) and \( U_{\text{T}} (t) \) are respectively the working state variables of the pump and generator unit, both of which are binary variables; \( P_{\text{P}}^{\hbox{max} } \) and \( P_{\text{P}}^{\hbox{min} } \) are respectively the maximum and minimum powers of the pumping unit; \( P_{\text{T}}^{\hbox{max} } \) and \( P_{\text{T}}^{\hbox{min} } \) are respectively the maximum and minimum powers of the generator unit.

3 Sizing optimization model considering demand response

3.1 Bi-level optimization

The bi-level optimization model is used to describe the sizing optimization of the island microgrid. The basic mathematical model is expressed as:

$$ S_{1} { = }\mathop {\hbox{min} }\limits_{x} F(\varvec{x},\varvec{z}) = \varvec{a}_{\text{1}} \varvec{x}{\mathbf{ + }}\varvec{b}_{\text{1}} \varvec{z} $$
(10)
$$ {\kern 1pt} \varvec{C}_{\text{1}} \varvec{x} \le \varvec{d}_{\text{1}} $$
(11)
$$ S_{2} { = }\mathop {\hbox{min} }\limits_{{\mathbf{z}}} f(\varvec{x}\text{,}\varvec{z}) = \varvec{b}_{\text{2}} \varvec{z} $$
(12)
$$ \varvec{C}_{\text{2}} \varvec{x}{\mathbf{ + }}\varvec{D}_{\text{2}} \varvec{z} \le \varvec{d}_{\text{2}} $$
(13)
$$ E(\varvec{x})\varvec{z} \le \varvec{d}_{\text{3}} $$
(14)

where the upper-level optimization model can be formulated as (10) and (11), and its optimization objective is to minimize the total cost. The decision variable \( \varvec{x} \) is an n-dimensional column vector representing the quantity or the capacity of the device. The formula (11) describes the constraints of the upper-level optimization. That is, the number or capacity constraints of the devices. Formulas (12), (13) and (14) describe the lower-level optimization, namely operational optimization, for which the optimization objective is to minimize the total shortage of electricity. The decision variable \( \varvec{z} \) is an m-dimensional column vector that represents the microgrid operational states. The lower-level optimization constraints include the power balance constraints, energy storage system operational constraints and demand response constraints, which can be divided into linear constraints (13) and nonlinear constraints (14). \( \varvec{a}_{\text{1}}, \varvec{b}_{\text{1}}, \varvec{b}_{\text{2}}, \varvec{d}_{\text{1}}, \varvec{d}_{\text{2}}, \varvec{d}_{\text{3}}, \varvec{C}_{\text{1}}, \varvec{C}_{\text{2}}, \varvec{D}_{\text{2}} \) are the matrix of the coefficient.

3.2 Sizing optimization

Generally, the rated power of the PV and wind turbine is fixed, and the optimization variables are \( N_{\text{PV}} \) and \( N_{\text{WT}} \). Similarly, the number of pumps, hydro-generator and reservoir are set to 1, and the optimization variables are \( P_{\text{P}}^{\hbox{max} } \), \( P_{\text{T}}^{\hbox{max} } \) and \( W^{\text{max}} \). The inverter capacity is matched with the total installed capacity of the PV and wind turbine, so there is no need to set the variable for the inverter. According to the above statements, the upper-level decision variables are:

$$ \varvec{x} = [N_{\text{PV}} ,N_{\text{WT}} ,P_{\text{P}}^{\hbox{max} } ,P_{\text{T}}^{\hbox{max} } ,W^{\text{max}} ] $$
(15)

The economic analyses of the microgrid are conducted using the annualized cost method. The annualized costs include the annual average cost of the initial investment, and the cost of replacement, operation, maintenance and demand response compensation and power shortage penalty. The objective function of the upper-level optimization can be described in detail as follows:

$$ \begin{aligned} S_{1} & = \hbox{min} F(\varvec{x}{\mathbf{,}}\varvec{z}) \\ & = \sum\limits_{{x^{1} \in G^{1} }} {C_{x}^{\text{NAV}} (N_{{x^{1} }} ,C_{{x^{1} }} ,u_{{x^{1} }} )} \\ {\kern 1pt} & \quad + \,\sum\limits_{{x^{2} \in G^{2} }} {C_{x}^{\text{NAV}} (R_{{x^{2} }} ,C_{{x^{2} }} ,u_{{x^{2} }} )} + \alpha E_{DR} (z) + \beta E_{{n{\text{o}}}} (z) \\ \end{aligned} $$
(16)
$$ 0 \le N_{{x^{1} }} \le N_{{x^{1} }}^{\hbox{max} } $$
(17)
$$ 0 \le R_{{x^{2} }} \le R_{{x^{2} }}^{\hbox{max} } $$
(18)
$$ G = [G^{1} ,G^{2} ] $$
(19)
$$ \varvec{x} \in G $$
(20)

where G is a collection of devices to be configured for the microgrid; \( G^{1} \) is a collection of devices, the number of which needs to be optimized, including photovoltaic panels, wind turbine and inverter; \( G^{2} \) is a collection of devices, the capacity of which needs to be optimized, including water pump, generator and reservoir; \( N_{{x^{1} }} \) is the number of device \( x_{1} \) with a maximum value of \( N_{{x^{1} }}^{\hbox{max} } \); \( R_{{x^{2} }} \) is the capacity of device \( x_{2} \) with a maximum value of \( R_{{x^{2} }}^{\hbox{max} } \); \( C_{x} \) is the annualized investment costs of device \( x \); \( u_{x} \) is the annual operational and maintenance cost of device \( x \); \( C_{x}^{NAV} \) is the annualized cost of device \( x \); \( \alpha \) is the compensation for deferrable load to participate in demand response per kWh; \( \beta \) is the economic loss cost of the unit shortage electricity; \( E_{DR} \) is the electricity of demand response; \( E_{no} \) is the total shortage of electricity and its calculation is introduced in detail in the next section.

\( C_{x}^{\text{NAV}} \) can be calculated by the following formulas:

$$ C_{x}^{\text{NAV}} = N_{x} \left[ {C_{x} \frac{{r_{0} (1 + r_{0} )^{m} }}{{(1 + r_{0} )^{m} - 1}} + u_{x} } \right] $$
(21)
$$ C_{x} (P_{x}^{\hbox{max} } ) = \sum\limits_{y = 1}^{m} {\frac{{C_{x} (P_{x}^{\hbox{max} } ,y)}}{{(1 + r_{0} )^{y} }}} - \frac{{S_{x} (P_{x}^{\hbox{max} } )}}{{(1 + r_{0} )^{m} }} $$
(22)
$$ S_{x} (P_{x}^{\hbox{max} } ) = C_{x} (P_{x}^{\hbox{max} } ,1)\left[ {\frac{{l_{x} (N_{r} + 1) - m}}{{l_{x} }}} \right] $$
(23)

where \( r{}_{0} \) is the discount rate; \( m \) is the engineering life; \( N_{x} \) is the number of devices; \( S_{x} \) is the residual value of the devices; \( C_{x} (P_{x}^{\hbox{max} } ,y) \) means the initial installation cost of the devices put into use at the beginning of the year \( y \) with the rated capacity of \( P_{x}^{\hbox{max} } \); \( l_{x} \) is the life span of device \( x \); \( N_{r} \) is the number of devices replaced during engineering life.

In this paper, it is assumed that the investment and operating costs of the device are linearly dependent on the rated capacity, that is:

$$ C_{x} (P_{x}^{{}} ) = C_{x} (N_{x}^{{}} P_{x}^{0} ) = N_{x}^{{}} C_{x} (P_{x}^{0} ) $$
(24)

where \( P_{x}^{0} \) is the unit rated capacity of the devices.

3.3 Operational optimization considering demand response

In this paper, the island load is divided into the non-deferrable load and the deferrable load. The non-deferrable load must be met during each time interval. The deferrable load, such as washing machines, can be flexibly arranged in another period. What needs to be emphasized is that deferrable appliances must get the user’s authorization to participate in demand response, and unauthorized parts will be considered as the non-deferrable load. Obtaining a minimum total shortage of electricity is the objective operational optimization.

$$ S_{2} = \hbox{min} E_{\text{no}} = \sum\limits_{t = 1}^{T} {(P_{\text{no}} (t)\Delta t)} $$
(25)

where T is the optimization period, and \( P_{\text{no}} (t) \) is the power shortage during the tth time interval.

Supposing there are a kind of deferrable household appliances (such as an electric water heater, washing machine, dishwasher, etc.) whose rated power is \( \Delta P \) and total number is \( N \), and all of them need to work once a day. Usually, the operating time of the appliances has the characteristic of randomness. To simplify the analysis, this paper assumes that when the demand response is not considered, the number of appliances working for a period time can be characterized by a known distribution according to the specific characteristics of the appliances. \( N(t) \) is the number of running deferrable appliances during the tth time interval. The lower layer decision variables \( \varvec{z} \) includes the power consumed by the pump (\( P_{\text{p}} (t) \)), the power generation (\( P_{\text{T}} (t) \)), the shortage power (\( P_{\text{no}} (t) \)), the volume of residual water in the upper reservoir (\( W(t) \)), state variables of the pump (\( U_{\text{P}} (t) \)) and state variables of the generator (\( U_{\text{T}} (t) \)) for each time interval.

Without considering the demand response, in addition to the aforementioned pumped storage system operational constraints, it is also necessary to meet the system power supply constraints:

$$ P_{{{\text{WT}}}} (t) + P_{{{\text{PV}}}} (t) + P_{{\text{T}}} (t) + P_{{{\text{no}}}} (t) \ge P_{{\text{P}}} (t) + P_{{\text{0}}} (t) + P_{{{\text{TLC}}}} (t)$$
(26)

where \( P_{0} (t) \) is the power of the non-deferrable load; \( P_{\text{TLC}} (t) \) is the power of all the available deferrable loads for the tth time interval without considering demand response.

Assume that the demand response participation degree of the appliances is \( \lambda \) which represents the proportion of the appliances that are authorized to participate in the demand response.

When the demand response is taken into consideration, it is necessary to meet the system power supply constraints as follows:

$$ P_{{{\text{WT}}}} (t) + P_{{{\text{PV}}}} (t) + P_{{\text{T}}} (t) + P_{{{\text{no}}}} (t) \ge P_{{\text{P}}} (t) + P_{{\text{0}}} '(t) + P'_{{{\text{TLC}}}} (t)$$
(27)
$$ P^{\prime}_{ 0} (t) = P_{ 0} (t) + (1 - \lambda )P_{\text{TLC}} (t) $$
(28)
$$ \lambda = \frac{{N^{\prime}}}{N} $$
(29)

where \( P^{\prime }_{0} (t) \) is the power of the total non-deferrable load including the deferrable load that is unauthorized to participate in the demand response.

Each appliance that is authorized to participate in the demand response will be numbered from 1 to \( N^{\prime } \). Number \( i \) identifies the appliance of\( i \). If the appliance of \( i \) can be transferred to the tth time interval from the t′th time interval, set the state variable as \( U_{{}}^{\text{IN}} (i,t^{\prime},t) \). \( U_{{}}^{\text{OUT}} (i,t,t^{\prime}) \) represents the state variable for the time interval from \( t \) to \( t^{\prime } \). Both \( U_{{}}^{\text{IN}} (i,t^{\prime},t) \) and \( U_{{}}^{\text{OUT}} (i,t,t^{\prime}) \) are binary variables. When the demand response is considered, the decision variables of the lower layer include \( P_{\text{P}} (t) \), \( P_{\text{T}} (t) \), \( P_{\text{no}} (t) \), \( W(t) \), \( U_{\text{P}} (t) \), \( U_{\text{T}} (t) \), \( U_{{}}^{\text{IN}} (i,t^{\prime},t) \) and \( U_{{}}^{\text{OUT}} (i,t,t^{\prime}) \).

\( P^{\prime }_{\text{TLC}} (t) \) is the power of the tth time interval considering demand response and it can be formulated as follows.

$$ \begin{aligned} P^{\prime}_{\text{TLC}} (t) & = P_{\text{TLC}}^{0} (t) \\ & \quad + \sum\limits_{i = 1}^{{N^{\prime}}} {\sum\limits_{{t^{\prime} = 1,t^{\prime} \ne t}}^{24} {[U_{{}}^{\text{IN}} (i,t^{\prime},t)} } - U_{{}}^{\text{OUT}} (i,t,t^{\prime})]\Delta P \\ \end{aligned} $$
(30)
$$ P_{\text{TLC}}^{0} (t) = \lambda P_{\text{TLC}} (t) = N^{0} (t)\Delta P $$
(31)

where \( N^{0} (t) \) is the number of appliances that participate in the demand response.

Demand response needs to meet the following 4 constraints:

  1. 1)

    The maximum power of the deferrable load that can be accepted in the tth time interval:

    $$ 0 \le P^{\prime}_{\text{TLC}} (t) \le P_{\text{TLC}}^{\hbox{max} } (t) $$
    (32)
  2. 2)

    State variables need to meet constraints:

    $$ \sum\limits_{{t^{\prime} = 1,t^{\prime} \ne t}}^{ 2 4} {[U_{{}}^{\text{IN}} (i,t^{\prime},t) + } U_{{}}^{\text{OUT}} (i,t,t^{\prime})] \le 1 $$
    (33)
  3. 3)

    The deferrable load is usually limited by the time interval that it can be transferred in:

    $$ U_{{}}^{\text{IN}} (i,t^{\prime},t) = 0,{\kern 1pt} {\kern 1pt} {\kern 1pt} t \in TS^{\text{N}} $$
    (34)

    where \( TS^{N} \) is the time interval that is not allowed to transfer in for the deferrable load.

  4. 4)

    Daily tasks must be completed:

    $$ N^{\prime}\Delta P = \sum\limits_{t = 1}^{24} {P^{\prime}_{\text{TLC}} (t)} $$
    (35)

3.4 Model solving

The lower layer optimization constraints are linear given the fixed upper layer decision variable \( \varvec{x} \). The operational optimization of the microgrid is a mixed integer linear programming (MILP). And the CPLEX is used to solve the operational optimization model by using the optimization interface (OPTI) of the MATLAB toolbox. Meanwhile, the sizing optimization model is solved by the particle swarm optimization (PSO) algorithm [23]. And the detailed solving steps are stated as follows:

Step 1: set the parameters of the PSO, and randomly initialize the position and velocity of each particle in the population.

Step 2: according to the configuration solution provided by each particle, use CPLEX to optimize the operation of the microgrid (the lower layer optimization), and calculate the fitness value of each particle.

Step 3: for each particle, compare the current fitness values with the fitness values of its optimal position, if the current fitness value is a better one, set the current location as the optimal position of the particle. And for all particles, compare each of the fitness values of the optimal location with the fitness values of the population optimal location, if the particles have a better fitness value, set the fitness value corresponding to the position as the current global optimal position.

Step 4: update the particle velocity and position; update the inertia weight.

Step 5: if the termination condition is met, stop the search and output the results; otherwise go to step 2.

4 Case studies

4.1 Parameters setting

The sizing optimization model proposed in this paper is applicable for island microgrids in different scales. In this paper, a small tropical island with little climate differences in the four seasons is used to conduct the case study. The island has abundant fresh water resources and does not need to use sea water desalination. The main electric load consists of the resident load. The annual average solar intensity is \( 5.5\;{\text{kWh/m}}^{ 2} / {\text{d}} \). The annual average wind speed is \( 7.3\;{\text{m/s}} \). The total number of households (about 3 people per household) is 32 and the number will remain stable for a long time period. The insular non-deferrable daily electricity load is 740 kWh (see Appendix Fig. A1). Deferrable appliances are smart water heaters with a storage function with a rated power of 2 kW. Cold water can be heated to the set temperature in one hour to meet the daily needs of hot water. The daily average electricity consumption of the island is 804 kWh and peak load is 100 kW.

In this case, the configuration optimization period is one week. Based on the average solar intensity, wind speed and the non-deferrable appliances daily average electricity consumption, the HOMER software is used to generate the typical solar intensity and wind speed data for one week (see Fig. 2) and the non-deferrable load data (see Fig. 3). Other related parameters of microgrid planning are set as follows: the DC bus voltage is 48 V, the AC bus voltage is 220 V; the engineering life (m) is 20 years, the discount rate (r0) is 0.05, the water head (h) is 100 m. The inverter conveyance efficiency is 95%, the efficiency of generator units is 0.64, the pump efficiency is 0.65, pipeline efficiency is 0.95, the maximum and minimum water storage capacity of the reservoir are 100% and 30% of the total capacity, respectively. The upper and lower limits of the operating power of the water pump and generator are 100% and 10%, respectively, and the device life cycle cost information is demonstrated in [11]. All the information for the devices is included in Appendix Table A1.

Fig. 2
figure 2

Solar intensity and wind speed of the island

Full size image
Fig. 3
figure 3

Non-deferrable load of the island

Full size image

Usually, the number of working water heaters in each time interval is not measured on the island. This paper assumes that when all the waterheaters do not participate in demand response, the number of water heaters that work in each time interval between 17–2400 hours are consistent with a known distribution, which gives a quite reasonable load profile that matches with the living habits of the residents. The typical daily load profile is shown in Fig. 4.

Fig. 4
figure 4

Typical daily load profile

Full size image

In the following discussion, the performance of the pumped storage scheme is compared with that of the battery storage scheme. The model of the battery storage system can be referred to in [20]. Battery (Dryfit A600) parameters are cited from the literature in [12]. 24 batteries are connected with a group within the 48 V DC bus in series. The decision variables of the battery storage scheme include the number of photovoltaic panels, wind turbines and the battery bank capacity. And the optimal configuration model of the battery storage scheme can be obtained by editing the model of the optimal configuration of the pumped storage system with considering the effect of the inverter conveyance efficiency on the energy storage system.

4.2 Configuration comparison of two different energy storage schemes

Under different demand response participation degrees, the configurations of the two energy storage schemes are shown in Table 1. The demand response participation degree of 0.00 indicates that there is no water heater participating in the demand response. Similarly, the demand response participation degree of 0.25 indicates that 25% of the water heaters are authorized to participate in the demand response. With the increase of DRPD, renewable energy installed capacity of the battery energy storage scheme changes little while the capacity of the energy storage system is gradually reduced, indicating that the demand response is helpful to reduce the capacity of the energy storage system. There is no obvious change trend in the rated power of the pump and generator units but more wind turbines and PV panels are installed in the pumped storage scheme for adding to the system’s lower comprehensive efficiency.

Table 1 Microgrid configuration with different DRPD
Full size table

Figure 5 shows the total cost of the two energy storage schemes under different DRPDs. With the increase of the DRPD, the cost of the microgrid configuration under the scheme of pumped storage and battery storage is gradually reduced. Although the comprehensive efficiency of the pumped storage is only 37.5%, far below the 81.0% of the battery storage, the pumped storage scheme can save more than 5.0% of the cost of the storage system compared with the battery energy storage scheme. In the microgrid total cost, the cost of the DRPD of 0.00 of the pumped storage system and battery storage system account for 52.0% and 59.0%, respectively. At the same time in the microgrid total cost, the cost of the DRPD of 1.00 of the pumped storage system and battery storage system account for 47.0% and 55.0%, respectively. This shows that the demand response helps to reduce the energy storage system cost.

Fig. 5
figure 5

Total cost with different DRPDs

Full size image

Although pumped storage scheme is equipped with more renewable energy installed capacity and the pumped storage system comprehensive efficiency is low, the lower cost and the longer life of the pumped storage make it more economical than that of the battery storage.

4.3 Operation analysis

As shown in Fig. 6, during the day when the sunshine is sufficient, the load demand is primarily met by the photovoltaic, and the surplus power is used to pump water. When there is no sunlight during the night, power demand can be satisfied by the pumped storage generator unit. Although the peak and valley differences increase when shifting the peak load to noon time from the evening, the renewable energy resources are better utilized. During the four day period, when all the deferrable load participates in the demand response, the discarded power of renewable energy generation is 2601 kWh. While there is no load to participate in the demand response, the discarded power of renewable generation is 2942 kWh, which means that 7.9% of the total load, in response to participating in energy consumption, is reduced by 11.5% of the discard amount of renewable energy. The demand response following the renewable energy power output can improve the utilization of available renewable energy.

Fig. 6
figure 6

24 hours of microgrid operation

Full size image

4.4 Sensitivity analysis

4.4.1 Total load

In this paper, the island load primarily consists of the resident load, and the load demand of all the residents is assumed to be similar, so the number of residents determines the total load. Under different total loads, the cost of the four different microgrid configurations is compared. PS-1 represents the cost of pumped storage with a DRPD of 1.00; PS-0 represents the cost of pumped storage with a DRPD of 0.00; BAT-1 represents the cost of battery storage with a DRPD of 1.00; and BAT-0 represents the cost of battery storage with a DRPD of 0.00. Figure 7 shows the costs under four different configuration schemes. We can see that the greater the number of households, the greater the load demand and the greater will be the costs of all four configurations. And it should be noted that the cost of PS-1 is the lowest while BAT-0 is significantly higher than the others under the same household numbers.

Fig. 7
figure 7

Cost comparisons under different household numbers

Full size image

Figure 8 shows the cost saving ratio of four configuration schemes. KPS(1-0) is the cost saving ratio of a DRPD of 1.00 compared to a DRPD of 0.00 under the pumped storage scheme. And KBAT(1-0) is the cost saving ratios of a DRPD of 1.00 compared to a DRPD of 0.00 under the battery storage scheme. K1(PS-BAT) represents the cost saving ratios of the pumped storage scheme compared to the battery storage scheme with a DRPD of 1.00. Similarly, K0(PS-BAT) represents the cost saving ratio of the pumped storage scheme compared to the battery storage with a DRPD of 0.00. As the load demand increases, the effect of the demand response on the cost saving ratio of the battery storage scheme is not obvious and KBAT(1-0) is about 9%. But increasing the load has a fluctuating effect on the cost saving ratio of the pumped storage scheme. At the same time, KPS(1-0) fluctuates between 8% to 11% and K1(PS-BAT) fluctuates between 5% to 9%.

Fig. 8
figure 8

Cost saving ratios under different household numbers

Full size image

4.4.2 DR compensation cost

As an important incentive for users to participate in demand response, demand response compensation in accordance with the demand response participation degree will be paid to island residents. In performina analyses on the cost composition of two schemes with different DRPDs, we can see a rapidly rising ratio of DR compensation cost to the total cost as more users participate in DR so that DR compensation cost cannot be ignored as part of the planning process (See Fig. 9).

Fig. 9
figure 9

Ratio of DR compensation cost to the total cost

Full size image

4.4.3 Water head of MPS

There are some construction requirements on the geographical environment of the island micro pumped storage system, especially related to the sea level and the geological conditions [24]. This subsection analyses the configuration of different water heads of a pumped storage system. Table 2 shows the investment costs of the microgrid under different water heads. With no restrictions on the construction of the reservoir, as the water head height is increased, the microgrid investment cost gradually decreases, i.e., a 100 m head compared to a 60 m head saves about 22% of cost. And the cost saving ratios under different DRPD changes vary slightly, with almost all being about 8%.

Table 2 Costs under different water heads
Full size table

5 Conclusion

In this paper, an island microgrid configuration model with a pumped storage system and considering the demand response participation degree is established. By analyzing an island microgrid case, the following conclusions are obtained:

  1. 1)

    Under suitable island geographical conditions, the use of a pumped storage scheme to replace the battery energy storage scheme and also improving the water head of the pumped storage system can help to reduce the cost of the microgrid investment.

  2. 2)

    Household appliances in demand response can improve the utilization of renewable energy and reduce the storage cost. Moreover, the more the load participation in the demand response, the more the cost is reduced.

  3. 3)

    In this paper, the proposed scheme is constrained by the island’s geographical conditions, if the construction of the pumped storage system capacity is limited, the shortage of electricity may increase, causing a sharp increase in the cost of the microgrid.