Self-tuning virtual synchronous generator control for improving frequency stability in autonomous photovoltaic-diesel microgrids

Abstract

This paper investigates the use of a virtual synchronous generator (VSG) to improve frequency stability in an autonomous photovoltaic-diesel microgrid with energy storage. VSG control is designed to emulate inertial response and damping power via power injection from/to the energy storage system. The effect of a VSG with constant parameters (CP-VSG) on the system frequency is analyzed. Based on the case study, self-tuning algorithms are used to search for optimal parameters during the operation of the VSG in order to minimize the amplitude and rate of change of the frequency variations. The performances of the proposed self-tuning (ST)-VSG, the frequency droop method, and the CP-VSG are evaluated by comparing their effects on attenuating frequency variations under load variations. For both simulated and experimental cases, the ST-VSG was found to be more efficient than the other two methods in improving frequency stability.

1 Introduction

Photovoltaic-diesel autonomous microgrids (MGs) are a good solution for electricity generation in isolated places where the solar resource is adequate. The MG is established by a diesel generator set (DGS) which is a controllable source of energy, and a solar generator is used to complement power production [1,2,3]. However, frequency variations of consequence are more likely to occur in islanded MGs than in large interconnected utility grids, because they feature a relatively small generation capacity and rapid changes in power demand, especially in the presence of stochastic renewable generators [4, 5]. In addition, if a reduced number of DGS units is not able to maintain frequency magnitude and rate of change within prescribed operational limits, tripping of renewable generators and loads can occur [6]. Therefore, the assistance of an energy storage system (ESS) is required to maintain frequency stability for the autonomous MG system.

A method that indirectly deals with dynamic frequency control is the smoothing of the output power of intermittent sources [7]. However, this method requires the measurements of the output powers, which needs a communication link to transmit the measurements. The frequency droop method can control the distributed power conversion systems (PCSs) solely by local measurements in a decentralized manner without using a communication link [8, 9]. Nevertheless, this approach is intended to support frequency regulation by using only a fixed form of frequency droop, thus it does not provide dynamic frequency support. In the virtual synchronous generator (VSG) concept, the power electronics interface of the ESS is controlled in a way to exhibit a reaction similar to that of a real synchronous generator (SG) to a change or disturbance [10,11,12,13].

Designing the CP-VSG to support dynamic frequency control involves emulating the inertial response and the damping power of a SG [14, 15]. The emulation of inertial response typically entails the control of power in inverse proportion to the first time derivative of the system frequency [14]. The damping power helps to attenuate oscillations, and thus to reduce the stabilization time of the frequency [15]. However, constant parameters do not explore the use of the variable virtual inertia and damping that can change their values during operation. In this regard, the VSG with self-tuning virtual inertia and damping, using the current control method (CCM), has been proposed to remove frequency oscillations [6].

Online optimization is used to calculate the inertial response and the damping power, which increases the computational burden of the digital signal processor (DSP). However, for MG applications, particularly considering the requirement for autonomous operation, the VSG is desired to operate using the voltage control method (VCM) as it can provide direct voltage and frequency support for the loads. Based on this fact, the bang-bang control strategy of alternating virtual inertia for the VSG operating with VCM has been proposed to suppress frequency and power oscillations effectively [16, 17]. During each cycle of oscillations, the value of inertia is switched between a big moment of inertia and a small one for four times. Each switching may cause power oscillations. On the other hand, applying a large constant virtual inertia for bang-bang control will result in a sluggish response. Besides, this method also does not explore the use of adaptive virtual damping that acts during the oscillation following a power disturbance. In order to overcome these limitations, a novel self-tuning (ST)-VSG based frequency control method is developed in this paper, which decreases the computational burden of the DSP and provides the self-tuning virtual inertia as well as virtual damping.

This paper starts with a brief introduction to the hierarchical control structure for an autonomous MG in Sect. 2. The CP-VSG-based frequency control scheme is developed and presented in Sect. 3. The proposed ST-VSG with self-tuning virtual inertia and virtual damping is analyzed in Sect. 4. The ST-VSG-based method is more efficient than the frequency droop method as well as the CP-VSG in attenuating frequency variations. A detailed comparison of these three methods is carried out in the simulation cases in Sect. 5. The corresponding experimental results are provided in Sect. 6. Finally, the main conclusion is highlighted in Sect. 7.

2 Proposed frequency hierarchical control structure for autonomous MG

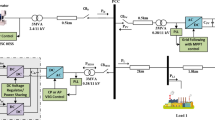
Figure 1 shows the proposed frequency hierarchical control structure for a photovoltaic-battery-diesel hybrid MG which consists of DGS, ESS, loads, photovoltaic unit and MG central controller. In Fig. 1, the photovoltaic unit is connected to the MG by a PQ-controlled inverter. Each distributed generator (DG) is composed of a circuit breaker and a power flow controller commanded by the central controller. The circuit breaker is used to disconnect the correspondent DG to mitigate the impacts of severe disturbances through the MG. Similarly, the point of common coupling switch is used to dynamically disconnect the MG from the utility grid for maintenance purposes or when grid faults or another contingency occurs. Although the MG can operate in either the grid-tied mode or islanded mode, only islanded operation will be considered in this paper.

Fig. 1

Hierarchical control structure of photovoltaic-battery-diesel MG

The proposed method to improve the frequency stability of an islanded photovoltaic-battery-diesel MG is based on hierarchical control. Primary control investigates the use of a PCS to support dynamic frequency control. In particular, the ST-VSG method proposed to support dynamic frequency control used the PSC to implement a frequency droop controller, self-tuning virtual inertia and virtual damping. However, an inherent limitation in the ST-VSG is the trade-off between frequency regulation and power sharing accuracy, and this may affect the frequency stability of the autonomous MG. Secondary control is used for power quality improvement by the DGS with a conventional PID speed governor. This control level eliminates frequency steady-state error generated by the ST-VSG. Tertiary control is by the central controller which facilitates high level management of the MG operation by means of technical and economical functions.

Note that secondary control is for compensating the deviations of voltage amplitude and frequency within the MG by conventional DGS functions [18]. Because of space limitations, the DGS model is not discussed here, and details can be found in [19]. Note also that tertiary control is for achieving global controllability of the MG. More details about secondary and tertiary controls are available in [20,21,22]. As a result, only the primary control scheme for dynamic frequency support in the autonomous MG is presented.

3 Principle of CP-VSG control strategy

The penetration of DGs in power systems is increasing rapidly. This increases the total system generation capacity, while it does not contribute to system rotational inertia. Because most DGs do not present rotational inertia, or are connected to the grid using switching converters, there may be inadequate balancing energy injection within the time frame of inertial response. The solution can be found in the control scheme of converter-based DGs. In the VSG concept, the power electronics interface of DG units is controlled in a way to emulate the inertial response and the damping power of a traditional SG.

3.1 CP-VSG control strategy

With the objective of paralleling PCSs and promoting the system frequency stability, the CP-VSG control strategy is introduced here. The control scheme is shown in Fig. 2, which comprises virtual inertia and damping emulators, active-power-frequency (ω-P) and reactive-power-voltage amplitude (Q-U) droop controllers, and a power calculation module [4].

Fig. 2

Block diagram of CP-VSG control strategy

The swing equation of the CP-VSG can be written as [23]:

$$P_{\text{ref}} - P_{\text{e}} - D_{\text{eq}} (\omega - \omega_{0} ) = J\omega \frac{{{\text{d}}\omega }}{{{\text{d}}t}} \approx J\omega_{0} \frac{{{\text{d}}\omega }}{{{\text{d}}t}}$$

(1)

where P _ref is the reference active power, P _e is the measured output average active power; D _eq = (1/m + Dω ₀) is the equivalent damping; m is the active power droop coefficient; ω ₀ is the nominal angular frequency; J is the virtual inertia. The virtual angular velocity ω is calculated by numerical integration and then the virtual phase angle θ is derived by passing through an integrator.

In order to extract the powers of fundamental frequency components, the instantaneous measured powers required to calculate CP-VSG operation are passed through low-pass filters (LPFs) with a cut-off frequency of 2 Hz to filter noise [24]. However, the filtering delay makes the frequency of systems with CP-VSG control change faster in both stand-alone mode and SG-connected mode [25]. Delayed-signal cancellation with multiple notch filters (DSC-MNFs) is proposed for harmonic elimination to extract the fundamental active and reactive powers.

For this paper, the power calculation principles in the synchronous rotating reference frame are formulated as:

$$P_{\text{e}} = \sum\limits_{y} {\frac{{s^{2} + \omega_{y}^{2} }}{{s^{2} + 2\zeta \omega_{y} s + \omega_{y}^{2} }}} \left[ {1.5(u_{od} i_{od} + u_{oq} i_{oq} } \right]$$

(2)

$$Q = \sum\limits_{y} {\frac{{s^{2} + \omega_{y}^{2} }}{{s^{2} + 2\zeta \omega_{y} s + \omega_{y}^{2} }}} \left[ {1.5(u_{oq} i_{od} - u_{od} i_{oq} } \right]$$

(3)

where u _odq and i _odq are the capacitor voltage and the output current, respectively; ω _y represents the system harmonic frequency and y denotes the dominant harmonic orders (y = 2, 4, 6, 8, 10, 12, …); ζ is the quality factor for the DSC-MNFs at the 2^nd harmonic frequency (it is set to ζ = 0.707 in this paper). The quality factor for the rest of harmonic frequencieccs is divided by their order.

In addition, the standard PI-based dual-loop control of the voltage and current is applied in this study to achieve power sharing stability [11]. The capacitor voltage control outer loop provides close voltage regulation and generates the reference current. The inductor current inner loop shapes the voltage across the filter inductor and generates pulses for space vector pulse width modulation (SVPWM).

3.2 Effects of CP-VSG on frequency transient

In order to analyze the effects of virtual inertia and virtual damping on a frequency transient, a simulation of an autonomous MG is developed according to Fig. 1. The parameters of the DGS and the CP-VSG used in simulation are presented in Tables 1 and 2 respectively.

Table 1 Main parameters of DGS

Table 2 Main parameters of CP-VSG

Figure 3a shows the system frequency with respect to virtual inertia J for a sudden increase of 100 kW load. It can be seen that the main effect of adding J to the system is that both the rate of change of frequency (RoCoF) and the peak frequency deviation decrease. However, a side effect of adding J is that the frequency will oscillate for a longer time before settling. Increasing the virtual damping D also produces a reduction in the peak frequency deviation, as can be seen in Fig. 3b.

Fig. 3

Effects of CP-VSG on frequency transient

Moreover, let J = 0 and D = 0, then the CP-VSG is equivalent to frequency droop control [26]. As for the comparison between each case, the CP-VSG is found to be more efficient than droop control in minimizing the amplitude and rate of change of the frequency variations.

4 Proposed ST-VSG control strategy

In this section, the frequency dynamic regulation mechanism of the CP-VSG in an autonomous MG is analyzed. Based on the analysis, a ST-VSG with self-tuning coefficients for virtual inertia and virtual damping is proposed. Moreover, the selection principle of self-tuning coefficients is given by referring to a small-signal model of the CP-VSG and a state-space model of the parallel system.

4.1 Frequency regulation mechanism of CP-VSG control

The swing equation of (1) can be rewritten as:

$$P_{\text{e}} = P_{\text{ref}} - P_{\text{D}} - P_{\text{J}} = P_{\text{ref}} - D_{\text{eq}} (\omega - \omega_{0} ) - J\omega_{0} \frac{{{\text{d}}\omega }}{{{\text{d}}t}}$$

(4)

Equation (4) has three terms. The first term, P _ref, is the reference value of active power that is the steady-state value of the output active power. The second term, P _D, emulates the damping power of a SG. The third term, P _J, emulates the inertial response of a SG. Both P _D and P _J are effective only during a transient to provide dynamic frequency support for the autonomous MG. Note that the virtual angular velocity ω is dictated mostly by the MG angular frequency ω _g when the CP-VSG is connected to the MG. Based on this fact, when the frequency of the MG starts to increase (dω _g/dt = dω/dt > 0), the CP-VSG which is in charge of emulating the inertial response starts to absorb power from the MG to prevent the frequency from rising too quickly, until the frequency reaches its maximum (dω/dt = 0). Then the frequency starts to decrease (dω/dt < 0) and the CP-VSG starts to inject power until steady state is achieved.

Considering (4), it is observed that the moment of J has a reverse relation to dω/dt, and the D has a reverse relation to ∆ω. For example, when frequency starts to deviate from steady state, a larger inertia would present a stronger opposition to the RoCoF, limiting its peak deviation. However, a larger inertia would no longer be required when frequency starts to return to steady state. On the other hand, the damping power is typically calculated from the ∆ω. Any deviation from steady state produces a power that attempts to bring the frequency back to steady state. Moreover, more damping would help to restore the system frequency faster.

4.2 ST-VSG control strategy

Despite the effectiveness of the CP-VSG, it does not explore the use of variable virtual inertia and virtual damping that can change their values during operation. In this regard, the ST-VSG control strategy is proposed to improve frequency stability for the autonomous MG. Assuming that the first oscillation of the frequency is the most critical one in terms of maintaining the system frequency stability, it might be a better approach to have self-tuning virtual inertia and virtual damping that are active only during a power disturbance.

Consider the frequency oscillation curve of Fig. 4. After a step load of 100 kW at t = 3 s in a typical 440 kW DGS, the operating point moves along the frequency curve, from point a to c and then from c to e. The self-tuning process of both J and D during each phase of an oscillation cycle is summarized in Table 3. One cycle of the oscillation consists of four segments. It should be noted that the sign of ∆ω (∆ω = ω − ω ₀) together with the sign of dω/dt defines the acceleration or deceleration of frequency during each segment. In other words, when ∆ω and dω/dt have the same signs in segments ① and ③, they are acceleration periods. Whereas, when ∆ω and dω/dt act in the opposite direction in segments ② and ④ when the frequency starts to go back to steady state, they are deceleration periods. When both ∆ω and dω/dt are equal to zero, it is a steady state period.

Fig. 4

Frequency oscillation curve of typical 440 kW DGS

Table 3 Self-tuning parameters of the ST-VSG control

The objective is to damp frequency oscillations quickly by controlling the acceleration and deceleration terms. For instance, a larger J would present a stronger opposition to both the RoCoF and the frequency deviation during acceleration phases (a to b and c to d). On the other hand, a smaller J would boost the deceleration of the frequency more rapidly during deceleration phases (b to c and d to e). In addition, a larger D would attenuate the frequency amplitude of the oscillations more quickly and stabilize the system faster in all segments.

Based on the above analysis, the self-tuning factors of virtual inertia and virtual damping are formulated as:

$$J = \left\{ \begin{gathered} J_{0} \begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} & {} \\ \end{array} } & {} & {{\text{|}}\Delta \omega | \le B} \\ \end{array} \hfill \\ J_{0} + k_{j} \left| {\frac{{{\text{d}}\omega }}{{{\text{d}}t}}} \right|\begin{array}{*{20}c} {} & {\Delta \omega \frac{{{\text{d}}\omega }}{{{\text{d}}t}} > 0\begin{array}{*{20}c} {} & {} & {{\text{|}}\Delta \omega | > B} \\ \end{array} } \\ \end{array} \hfill \\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\begin{array}{*{20}c} {} & {\Delta \omega \frac{{{\text{d}}\omega }}{{{\text{d}}t}} \le 0\begin{array}{*{20}c} {} & {} & {{\text{|}}\Delta \omega | > B} \\ \end{array} } \\ \end{array} \hfill \\ \end{gathered} \right.$$

(5)

$$D = \left\{ \begin{gathered} D_{0} \begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} & {} \\ \end{array} } & {} & {{\text{|}}\Delta \omega | \le B} \\ \end{array} \hfill \\ D_{0} + k_{d} \left| {\Delta \omega } \right|\begin{array}{*{20}c} {} & {{\text{|}}\Delta \omega | > B} \\ \end{array} \hfill \\ \end{gathered} \right.$$

(6)

where J ₀ and D ₀ are the steady state values of J and D, respectively; k _j and k _d are the regulation coefficients of J and D, respectively; B is the threshold value for ∆ω. The ST-VSG is operating with the normal values of J ₀ and D ₀ in the case of steady state. During each cycle of oscillations, the value of J is switched four times. Each switching happens when the sign of either ∆ω or dω/dt changes.

When the disturbance occurs, the transition from a to b starts with ∆ω < 0 and dω/dt < 0. In the acceleration term, the value of J is increasing with the absolute value of dω/dt multiplied by k _j . At the end of the first quarter-cycle, that is point b, the sign of dω/dt changes, and the value of J is set to zero in the deceleration term. At point c, the sign of ∆ω changes and J returns to a big value in the acceleration term. During the second half-cycle, the value of J is switched to zero at point d, and to a big value at the end of one cycle at point e. This procedure is repeated for each cycle of oscillation until the transients are suppressed. Considering (6), the value of D is increasing with the absolute value of ∆ω multiplied by k _d during the whole cycle of oscillation. Note that the value of B is used to avoid the chattering, or rapid and unhelpful changes, of J and D during the sign changes of ∆ω and dω/dt, and is set to 0.3 rad/s in this paper.

4.3 Selection scheme for self-tuning coefficients

The values of J together with D determine the stability and the dynamic response of the VSG system. Selecting proper values for them is a challenging issue and requires analysis. A small-signal model of the CP-VSG with different values of J and D is built to illustrate transient responses of output power during a loading transition.

In the control of the CP-VSG for frequency stability, the sending side of the system can be drawn as a two-machine system as shown in Fig. 5. The output apparent power S of the CP-VSG can be written as:

$$S = P_{\text{e}} + {\text{j}}Q = \frac{UE}{X}{ \sin }\delta + {\text{j}}\frac{{UE{ \cos }\delta - E^{2} }}{X}$$

(7)

where E is the output voltage of the DGS; X is the distribution line reactance; δ ₁ is the rotor angle of the CP-VSG; δ ₂ is the rotor angle of the DGS; δ =δ ₁ − δ ₂, is the power angle of the CP-VSG. Let sinδ ≈ δ, and K =UE/X which is the synchronizing power factor, so that the output active power P _e can be approximated as:

$$P_{\text{e}} = \frac{UE}{X}{ \sin }\delta \approx \frac{UE}{X}\delta = K\delta$$

(8)

Fig. 5

Diagram of two machines PCS and DGS

Knowing that δ=∫(ω-ω ₀)dt, (8) becomes:

$$\left\{ {\begin{array}{*{20}c} {\frac{{{\text{d}}P_{\text{e}} }}{{{\text{d}}t}} = K\frac{{{\text{d}}\delta }}{{{\text{d}}t}} = K\left( {\omega - \omega_{0} } \right)\begin{array}{*{20}c} {} & {} \\ \end{array} } \\ {\frac{{{\text{d}}^{2} P_{\text{e}} }}{{{\text{d}}^{2} t}} = K\frac{{{\text{d(}}\omega - \omega_{0} )}}{{{\text{d}}t}} = K\frac{{{\text{d}}\omega }}{{{\text{d}}t}}} \\ \end{array} } \right.$$

(9)

Replace (9) in (4), so that

$$P_{\text{ref}} = P_{\text{e}} + \frac{{D_{\text{eq}} }}{K}\frac{{{\text{d}}P_{\text{e}} }}{{{\text{d}}t}} + \frac{{J\omega_{0} }}{K}\frac{{{\text{d}}^{2} P_{\text{e}} }}{{{\text{d}}^{2} t}}$$

(10)

The transfer function, considering the reference value of the active power P _ref as the input, is:

$$G(s) = \frac{{P_{\text{e}} \left( s \right)}}{{P_{\text{ref}} \left( s \right)}} = \frac{K}{{J\omega_{0} s^{2} + D_{\text{eq}} s + K}}$$

(11)

According to (11), the standard parameters for a second-order transient response can be defined as:

$$\left\{ \begin{gathered} \omega _{{\text{n}}} = \sqrt {\tfrac{K}{{J\omega _{0} }}} \hfill \\ \xi = \frac{{D_{{{\text{eq}}}} }}{2}\sqrt {\tfrac{1}{{KJ\omega _{0} }}} = \frac{{1/m + D\omega _{0} }}{2}\sqrt {\tfrac{1}{{KJ\omega _{0} }}} \hfill \\ \end{gathered} \right.$$

(12)

where ω _n is the natural oscillation frequency; ξ is the damping ratio. Note that the value of the active power droop constant m is calculated according to the maximum allowable steady-state frequency deviation of 1% and to the maximum active power reserve of 100%. Here, m = 1% × 50 × 2π/100000 = 3.1e⁻⁵ rad/s/w for a 100 kVA PCS.

Based on (11), it is possible to calculate the step responses of output active power of the CP-VSG with various parameters, and the results are shown in Fig. 6. Parameters used for both theoretical calculation and simulation are the same, as listed in Table 2. From (12) and Fig. 6, it is observed that the virtual inertia determines the oscillation of the frequency, whereas the virtual damping determines the attenuation speed of oscillations of the frequency.

Fig. 6

Step responses of CP-VSG output power with various parameters

The higher H, the higher the system inertia, resulting in a smaller frequency deviation after a change in active power load or supply. For typical large SGs used in power plants, H varies between 2 and 10 s. For this case, a value of 4 s has been chosen, as it is a good representation for an autonomous MG with reduced inertia, which is exactly the condition in which the CP-VSG provides a solution for enhancing frequency stability. Calculating J for a CP-VSG with a rated output power of 100kW using (2), results in inertia J = 2 × 4 × 100000/(100π)² = 8.1 kg m². Considering an optimal second-order quality factor of ξ = 0.707 for the DSC-MNFs, and for U = 380 V, E = 380 V, X = 0.63 Ω, results in D = 6.4 p.u. according to (12).

A state-space model of the parallel system with the selected values of J and D is built to analyze its stability and dynamic response. The swing equations of the CP-VSG and the DGS in Fig. 5 can be written as:

$$H\frac{{{\text{d}}^{2} \delta_{1} }}{{{\text{d}}t^{2} }} + D\frac{{{\text{d}}\delta_{1} }}{{{\text{d}}t}} = P_{\text{m}} - P_{\text{e}}$$

(13)

$$H_{2} \frac{{{\text{d}}^{2} \delta_{2} }}{{{\text{d}}t^{2} }} + D_{2} \frac{{{\text{d}}\delta_{2} }}{{{\text{d}}t}} = P_{\text{m2}} - P_{\text{e2}}$$

(14)

where H ₂, D ₂, P _m2, P _e2 are the inertia constant, damping factor, mechanical power and electrical power of DGS, respectively. Linear approximation for the swing equations of CP-VSG and DGS can be represented as [27]:

$$\left[ \begin{aligned} \Delta \dot{\delta } \hfill \\ \Delta \dot{\omega } \hfill \\ \end{aligned} \right] = \left[ {\begin{array}{*{20}c} 0 & 1 \\ { - MK_{s} } & { - N} \\ \end{array} } \right]\left[ \begin{aligned} \Delta \delta \hfill \\ \Delta \omega \hfill \\ \end{aligned} \right]$$

(15)

where M = (H + H ₂)/(HH ₂); N = (DH ₂ − D ₂ H)/(HH ₂); K _s  = Kcosδ ₀; δ ₀ is the operating point of δ. The system stability is determined by the eigenvalues shown in (16).

$$\lambda_{1,2} = - N/2 \pm \sqrt {N^{2} /4 - MK_{s} }$$

(16)

The value of K _s can be calculated as follows:

$$K_{s} = K\cos \delta_{0} = K\sqrt {1 - (\sin \delta_{0} )^{2} }$$

(17)

The output active power P _e of the CP-VSG in Fig. 5 can be defined as P _e = Ksinδ ₀. Then the value of K _s can be expressed as:

$$K_{s} = K\sqrt {1 - (\sin \delta_{0} )^{2} } = \sqrt {\left( {\frac{EU}{X}} \right)^{2} - P_{\text{e}}^{2} }$$

(18)

Since this is very large (K = UE/X = 229.2 W, and the maximum value of P _e is 100 kW for the 100 kVA CP-VSG), the value in the square root of (16) is negative. Thus, the second term of (16) is the imaginary part of the eigenvalues. When N > 0, i.e., D/H > D ₂/H ₂, the system maintains stability. Let D ₂ = 0.38 p.u. and H ₂ = 0.77 s, which are obtained according to [22] for a 440 kW DGS, and then D/H > 0.49, i.e., D > 1.96 p.u..

Therefore, the CP-VSG with fixed values of J = 8 kg·m² and D = 6 p.u. can ensure good stability and fast dynamic response for the autonomous MG. Consequently, selecting the values of RoCoF_max = 2.5 Hz/s, J ₀ = 2 kg·m² and J _max = 8 kg m², results in k _j  = (8-2)/(2.5 × 2π) = 0.38 for the ST-VSG. In contrast, the values of D ₀ = 2 p.u. and k _d  = 4.1, are selected in this paper. This is because, when the value of the frequency deviation is 0.2 Hz, a larger damping (D = 4.1 × 0.2 × 2π + 2 = 7.1 p.u. > 6 p.u.) would present a stronger opposition to the frequency deviation, reducing the frequency oscillation and its stabilization time.

5 Simulation validation by experiment

The performances of the proposed ST-VSG, the frequency droop method and the CP-VSG are evaluated by comparing their effects on frequency stability under load variations. The same autonomous MG is studied including a 100 kVA PCS, adjustable loads and a 440 kW DGS as shown in Fig. 1. Parameters used in simulations are summarized in Tables 1, 2 and 4. For simpler presentation, considering that this paper addresses frequency control, only active power is shown.

Table 4 Parameters of virtual inertia and virtual damping

This test consists of a step load increase of 100 kW at t = 3 s from an initial load of 100 kW (the PCS supplies 20 kW, the DGS supplies 80 kW) while a 440 kW DGS is connected to a 100 kVA PCS with droop control. The same tests are conducted for the PCS with the CP-VSG control and the ST-VSG control, respectively. Figure 7 shows the simulation results, where the curve labeled “Droop” is the response of the DGS plus the PCS with droop control, “CP-VSG” is the response of the DGS plus the PCS with CP-VSG control, and “ST-VSG” is the responses of the DGS plus the PCS with ST-VSG control.

Fig. 7

Effects of frequency droop method, CP-VSG and ST-VSG on MG frequency

Figure 7a shows the system frequency with respect to the PCS using different methods. It can be noted that the curve “CP-VSG” presents a frequency nadir that lies between the other two curves. It means that the CP-VSG is more efficient than droop control in reducing the RoCoF and the frequency deviation by providing virtual inertia and virtual damping. The curve “ST-VSG” presents a frequency nadir that lies above the curve “CP-VSG”. Overshoot of the frequency is effectively suppressed by the ST-VSG. As can be noted, the self-tuning virtual inertia and virtual damping provided by the ST-VSG increase the equivalent inertia and damping of the system, reducing the maximal frequency deviation. As a trade-off, the PCS with the ST-VSG control needs to deliver more energy into the autonomous MG than the other two methods as shown in Fig 7b, which indicates that the ESS should be equipped with a larger capacity. However, with the help of the ST-VSG, the DGS delivers the least transient power to copy with the load mutation as can be seen in Fig. 7c. Hence, the ST-VSG obtains the best frequency stability for the autonomous MG, as the rotational speed of the DGS is proportional to its transient output active power.

On the other hand, Fig. 8 shows the frequency- acceleration curves for the PCS using different methods. The curve labeled “Droop” is the response of the DGS plus the PCS with droop control, “CP-VSG” is the response of the DGS plus the PCS with CP-VSG control, and “ST-VSG” is the responses of the DGS plus the PCS with ST-VSG control. It is observed that the curve “ST-VSG” presents the RoCoF and the deviation of frequency with respect to the nominal value that lies inside the other two curves. This means that the ST-VSG is the most efficient method for attenuating the amplitude and rate of change of the frequency variations.

Fig. 8

Frequency-acceleration curves for different methods

The simulation results for virtual inertia and virtual damping of the ST-VSG are shown in Fig. 9. It can be seen that ST-VSG control increases its virtual inertia rapidly in the acceleration terms, but makes its virtual inertia equal to 0 in the deceleration terms as shown in Fig. 9a. On the other hand, it increases its virtual damping in the whole cycle of oscillation as shown in Fig. 9b. This emphasizes that the proposed ST-VSG strategy entails the self-tuning variations of the VSG parameters of virtual inertia and virtual damping during the operation of the VSG.

Fig. 9

Self-tuning factors of virtual inertia and virtual damping

6 Experimental results

The proposed control method is verified experimentally using a laboratory-scale autonomous MG, developed according to the block diagram from Fig. 1. The MG consists of a 440 kW DGS, two 100 kVA PCS units, and two 10 kVA photovoltaic inverters as illustrated in Fig. 10. A three-phase power supply rectified by a controllable bidirectional IGBT bridge is used to imitate the dc output of a ESS or a solar PV generator. The experimental setup parameters are the same for the simulation cases. A 200 kW controllable load is included to create dynamic events in the MG. Each PCS is controlled by an independent DSP TMS320F28335, which implements the proposed control schemes, as described in the previous sections.

Fig. 10

Laboratory diagram of photovoltaic-battery-diesel MG

Experiments were performed under three test cases in order to verify again the effectiveness of the proposed ST-VSG. In Case 1, two PCSs are operating with different methods including droop control and ST-VSG when the MG islanding occurs, respectively. This scenario evaluates the frequency control capability of the ST-VSG operating in the islanded mode. In Case 2, the parallel operation of a CP-VSG and a DGS is analyzed in order to determine the effect of the virtual inertia and virtual damping on the frequency performance. In Case 3, the performances of the ST-VSG, the droop method and the CP-VSG are evaluated by comparing their effects on minimizing the amplitude and rate of change of the frequency variations under load variations. In all cases the transitory regime is created by switching the load on after an interval of steady-state operation.

• 1) Case 1

This scenario is characterized by switching in an additional 100 kW load. The test results for the system frequency f and the output currents (i _o1 and i _o2) of the two 100 kVA PCSs are shown in Fig. 11.

Fig. 11

Measured effects of droop method and ST-VSG on system frequency

Note that the droop control as well as the ST-VSG obtains a fast dynamic performance to respond to the load variations and achieves a good current sharing capability. It can be seen that the ST-VSG is more efficient than the droop control in attenuating the RoCoF due to the provided virtual inertia.

Figure 12 shows the output active powers (P _e1 and P _e2) of the two 100 kVA ST-VSG units when the additional 100 kW load is connected. Observe that the proposed power filter method can effectively improve the dynamic performance of the system, given that the response time ranges from about 44 ms when using the LPF method to 12 ms when using the DSC-MNF method.

Fig. 12

Measured active power output waveforms of two ST-VSG units under 100 kW load connection condition

• 2) Case 2

Section 3.2 described the two parameters that the CP-VSG has which can influence the frequency performance: the virtual inertial J and the virtual damping D. To analyze the influence of these parameters, Case 2 consists of a step load increase of 100 kW from an initial load of 100 kW (the CP-VSG supplies 20 kW and the DGS supplies 80 kW) while the DGS is connected to the 100 kVA CP-VSG unit.

Figure 13a shows the experimental results for different values of virtual inertia (J = 0, 2, 4 kg m²) without any damping. As can be seen, the virtual inertia has a great impact on reducing the RoCoF as well as the peak frequency deviation. However, a side effect of adding virtual inertia is that the frequency will oscillate for a longer time before returning to its steady state.

Fig. 13

Measured effects of CP-VSG on autonomous MG frequency

Virtual damping was also tested. In this case, different values of virtual damping (D = 0, 2, 6 p.u.) were tested without any inertia. Fig. 13b concords with Fig. 3b. That is, increasing the virtual damping produces a reduction in the peak deviation as well as the amplitude of the frequency variations. It implies that more damping would help to stabilize the system frequency faster. These statements are similar to those found in Sect. 3.2.

• 3) Case 3

This test consists of a step load increase of 100 kW at t = 2 s from an initial load of 100 kW (the PCS supplies 20 kW, the DGS supplies 80 kW) while the 440 kW DGS is connected to one of the 100 kVA PCSs. Figure 14 shows the experimental results, where the curve labeled “Droop” is the response of the DGS plus the PCS with droop control, “CP-VSG” is the response of DGS plus the PCS with CP-VSG control, and “ST-VSG” is the response of DGS plus the PCS with ST-VSG control.

Fig. 14

Measured effects of droop control, CP-VSG and ST-VSG on MG frequency

From Fig 14a, it is observed that the curve “ST-VSG” presents a frequency nadir that lies above the other two curves and the frequency overshoot is suppressed effectively. This is because the ST-VSG makes its virtual inertia increase in the acceleration phase, but makes its virtual inertia equal to zero in the deceleration phase according to (10). The virtual damping is self-tuning to keep a larger value in the whole cycle of oscillation according to (11). As a result, the average active power injected into the system by the ST-VSG is much more than either the CP-VSG or the droop method, as can be seen from Fig. 14b. From Fig. 14c, it is observed that with the help of the ST-VSG, the DGS presents the lowest average output active power under the step load condition. Hence, the highest frequency stability for the autonomous MG is achieved by the ST-VSG, as the transient output active power of the DGS is proportional to the RoCoF and the peak frequency deviation.

The frequency-acceleration trajectories of the PCS with different control methods are shown in Fig. 15. The curve “Droop” refers to the PCS with the droop control and without any virtual inertia and damping, and the maximal absolute values of the RoCoF and frequency deviation are 5.42 Hz/s and 0.6 Hz, respectively. Whereas the curve “CP-VSG” refers to the PCS with CP-VSG control, and the maximal absolute values of the RoCoF and frequency deviation are reduced to 3.43 Hz/s and 0.44 Hz, respectively. It can be seen that the area enclosed by the trajectory is decreased because of the virtual inertia and virtual damping provided by the CP-VSG reduce the RoCoF as well as the peak frequency deviation. The frequency-acceleration curve of the PCS with ST-VSG control is marked with “ST-VSG”. It is observed that the trajectory is forced to converge even faster by varying the acceleration or deceleration magnitude by using the self-tuning virtual inertia and virtual damping in each section of an oscillation cycle.

Fig. 15

Measured frequency-acceleration curves with droop control, CP-VSG and ST-VSG

On the other hand, Fig. 16 shows the test results for variations for virtual inertia and virtual damping of the ST-VSG. It can be seen that the ST-VSG makes its virtual inertia equal to zero in the deceleration phases as shown in Fig. 16a, and increases its virtual damping during the whole cycle of oscillation as shown in Fig. 16b. The maximal absolute values of the RoCoF and the frequency deviation (as shown in Fig. 15) are reduced to 2.5 Hz/s and 0.31 Hz, respectively. Therefore, it can be said that the ST-VSG achieved a better performance in improving the frequency stability than either the CP-VSG or the droop method.

Fig. 16

Measured self-tuning factors of virtual inertia and virtual damping

7 Conclusion

In this paper, the novel strategy of an ST-VSG was elaborated. This self-tuning method allows a VSG to increase and reduce its virtual inertia and virtual damping according to its virtual angular velocity and acceleration/ deceleration in each phase of frequency oscillation. By selecting an increased virtual inertia during acceleration, the RoCoF is mitigated, and on the other hand, during deceleration, a zero virtual inertia is adopted to increase the deceleration effect. In addition, by using increased virtual damping during the whole cycle of oscillation, both the deviation and the overshoot of system frequency are reduced effectively.

The performances of the droop method, the CP-VSG and the ST-VSG were evaluated by comparing, in simulation and by experiment, their dynamic frequency responses for different scenarios of load variation in an autonomous MG. The main results obtained in the simulation as well as the laboratory test results are presented. These results illustrate that the major advantages of the proposed ST-VSG are the reductions of the initial RoCoF and the maximum frequency deviation, these being the important issues for the stability of system frequency.

The performance and capability of the control strategy presented in this work directly depend on the ESS, i.e., the energy storage device and the power electronic converter. It is important to bear in mind that, depending on the type of load variation, the operation of the proposed ST-VSG results in a greater discharge of the ESS when compared to the droop method or CP-VSG. This suggests that future work should be directed at obtaining some guidelines in order to specify the ESS according the self-tuning virtual inertia and virtual damping. On the other hand, it could be also useful to coordinate the state of charge of the ESS in the ST-VSG control strategy.