Abstract
Modern power systems, employing an increasing number of converter-based renewable energy sources (RES) and decreasing the usage of conventional power plants, are leading to lower levels of short-circuit power and rotational inertia. A solution to this is the employment of synchronous condensers in the grid, in order to provide sufficient short-circuit power. This results in the increase of the short-circuit ratio (SCR) at transmission system bus-bars serving as points of interconnection (POI) to renewable generation. Evaluation of the required capacity and grid-location of the synchronous condensers, is inherently a mixed integer nonlinear optimization problem, which could not be done on manual basis considering each type of machine and all bus-bars. This study therefore proposes a method of optimal allocation of synchronous condensers in a hypothetic future scenario of a transmission system fed by renewable generation. Total cost of synchronous condenser installations in the system is minimized and the SCRs at the POIs of central renewable power plants are strengthened. The method has potential for application on larger grids, aiding grid-integration of RES.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
During the last decades, changes have occurred in the planning of new generation units, on the basis of environmental problems caused by the use of traditional generation plants relying on fossil-fuels. The shift from large conventional generating units to smaller-scale plants converting renewable energy sources (RES), such as wind and solar radiation, in electrical energy, is leading to new challenges for grid operators. On top of this, HVDC interconnections are being established, resulting in the development of cross-border electricity markets which allow accommodation of these new RES: e.g. the HVDC interconnections Skagerrak 1–4 are used to balance wind-generation in Denmark with hydro-generation from Norway [1]. These changes are especially relevant for countries like Denmark, where the national transmission system operator (TSO) Energinet.dk’s analysis assumptions for the period 2014–2035, expects the expansion of wind-generation capacity in Denmark up until 2036 [2]. At the same time, Energinet.dk is expecting to reduce the need for central power plants to a minimum or rule them out completely from the western part (DK1) of the transmission system [3].
Wind farms of recent installation, such as Horns Rev 3 in Western Denmark, employ type IV wind turbine generators (permanent-magnet-generator with a full-scale power converter) [4], which have the advantage of better active/reactive power control, the possibility of gear-box removal and reduced mechanical stress on the turbine, compared to the older fixed speed types [5].
The presence of full-scale power converters in type IV wind turbines combined with the shut-down of the conventional synchronous generator based power plants is the main cause of diminishing the short-circuit power of the grid, as the quantities provided by these RES are lower than those of conventional plants using synchronous generators [6]. Whereas fixed speed wind turbines contribute to inertia, the contribution of the more recent variable speed turbine types is zero [7]. Following a disturbance in the system (e.g. loss of generator), type I-II wind turbine generators which are directly connected to the grid, release the stored kinetic rotational energy in the generator, blades and gearbox [8], limiting change of rotor speed caused by the variation of system frequency [9]. Type III–IV wind turbine generators are instead not capable of this, since the frequency converter, decouples the turbine rotor speed from grid frequency [7]. In response to the declining of system inertia, some system operators could require in their grid-connection codes a certain level of “artificial inertia” to be supplied by low inertia generators [10]. Control schemes based on model predictive control (MPC) presented in [11], might implement this through use of internal/external sources of power such as energy storage devices. In this manner, frequency variations may be resisted until the intervention of appropriate frequency controllers. This presents tough challenges such as tractability in real-time and observance of tight operational constraints [11].
Regarding short-circuit power, the design of the power converter of type IV wind turbines limits the maximum short-circuit current output to 1.1–1.2 per-unit [12]. The limitation of short-circuit power is significant since it affects the short-circuit ratio (SCR) at AC terminals of the major converter stations. Insufficient SCR could cause numerous problems to the voltage stability and dynamic behaviour of converter stations [1].
The IEEE standard n.1204-1997 in [13] defines the critical SCR value equal to 2 and uses this quantity to measure the strength of an AC system with respect to the rated active power at the DC terminal of a thyristor-based converter. Reference [14], evaluates instead the SCR in relation to the wind farm’s point of interconnection (POI). It considers a critical SCR value of 3, above which a system is considered sufficiently strong and able to minimize the variation of system variables (e.g. frequency, voltage, etc.), following a disturbance.
A solution to situations involving grids with low inertia and SCRs, recommended in [13] is the installation of synchronous condensers/compensators. This has already been implemented at various nodes of the Danish transmission system operated by Energinet.dk: in particular at LCC type HVDC terminal substations [16]. Synchronous condensers are substantially synchronous generators with no prime-mover: the mechanical shaft is unloaded. Historically, they have been used for reactive power support and are now employed through new installations or refurbishment of conventional generators or as standalone condensers for sustaining grid rotational inertia and short-circuit capacity [15], after the retirement of synchronous generators.
Planning of these devices, needs therefore to be addressed in a system rich in RES, in order to save cost with respect to the application. Manually, listing all possible combinations of rated power capacities at the system POIs where the SCR is deemed insufficient, would work merely in specific cases. Major electrical power-grids contain hundreds of nodes, that makes this combinatorial process difficult to handle. While system operators are also subject to cost constraints when evaluating new installations. As a result, optimization models are necessary to consider simultaneously the location, capacities and optimal installation cost of the devices.
The application of synchronous condensers proposed in the paper is relatively new to the common practice, though the optimization method genetic algorithm (GA) used here as a tool has been applied to reactive power planning [17, 18]. GA is a heuristic technique based upon evolutionary theory [19,20,21] developed to solve problems with a degree of complexity that can not be solved by mathematical based methods [19]. Genetic algorithms use selection, mutation and cross-over operations to transform a random initial population into a new one, with the aim of improving the fitness of a solution associated to the objective function [17].
Reference [22] deals with the optimization of dynamic reactive power sources, including synchronous condensers, through the implementation of a mixed integer nonlinear optimization method taking into account system dynamics and grid-code requirements of wind turbines. In the study, DIgSILENT PowerFactory was used as solver for differential equations and system time-domain calculations, whereas MATLAB implemented the optimization routines. These programmes have also been used in [23], where an automatic data exchange was implemented between the two programmes.
This paper aims proposing an optimization model and reporting the practice for grid operators to evaluate and optimize the need of synchronous condensers for future weak systems with renewable generation. The case study is implemented in a futuristic wind dominated low inertia system scenario of the Western Danish system, with a reasonable assumption of limited choices for grid operators over synchronous condenser types and quantities. Although inertia is not considered in the calculations and system dynamic behaviour is neglected for simplicity, the property of short-circuit power of a low inertia system is preserved due to the lack of sufficient synchronous generator capacity. The contribution of the work here presented, is a simple computational procedure, able to optimize the selection and allocation of synchronous condensers in power systems with large quantities of static-converter based RES.
The rest of the paper is organized as follows. Section II presents the problem formulation. Section III describes the methodology used to optimally allocate synchronous condenser installations in systems having weak bus-bar nodes at wind farm POIs. In Section IV a modified Western Danish transmission system DK1 representing a low inertia system is presented and used to conduct case studies evaluating strength for system configurations, with and without synchronous condensers. The results found are then discussed under Section V, dedicated to the final conclusions.
2 Problem formulation
2.1 Short circuit ratio
As mentioned previously, the goal here is to ensure adequate strength at the POIs connected to static converter-based renewable generation keeping total allocation cost of synchronous condensers as low as possible. Strength of the individual POI is evaluated through calculation of the SCR as (1) [13, 14]:
where i is the candidate bus-bar; SCR i is the SCR at the i-th bus-bar; \(S_{k}^{\prime \prime i}\) is the short-circuit power level at the i-th bus-bar excluding the wind farms connected to that specific bus-bar/POI; P i n is the wind-generation nominal active power installed at the i-th bus-bar.
It is assumed based on [13, 14] that sufficient strength at the specific bus-bar is obtained when the SCR is at least equal to 3. This requires though, knowledge of the short-circuit power level \(S_{k}^{\prime \prime i}\).
2.2 Short-circuit power level
Calculation of short-circuit quantities can give different results, depending on the standard adopted and whether interest is placed upon network planning or operation. In this paper, short-circuit calculations are carried out according to the IEC 60909 standard, since it is a widely adopted standard for grid planning purposes [6, 24].
According to the standard, the initial symmetrical short-circuit power is derived from the initial symmetrical three-phase short-circuit current (2) [25, 26]:
where \(I_{k}^{\prime \prime i}\) is the initial symmetrical three-phase short-circuit current at the i-th bus-bar, and \(U_{n}^{i}\) is the nominal line-to-line voltage at the \(i\)-th bus-bar.
Based on (2), since the short-circuit power level is the only quantity of interest, in order to compute the SCR, only balanced three-phase short-circuit calculations are investigated.
The initial three-phase symmetrical short-circuit current is calculated from (3) [25, 26]:
where \(Z_{k}^{i}\)is the Thevenin equivalent short-circuit impedance magnitude as seen from the \(i\)-th bus-bar, and \(c\) is a voltage factor which takes into consideration the voltage variations in the network.
IEC 60909 defines maximum and minimum values of short-circuit power. These are calculated using different network configurations: e.g. different values of \(c\) for ac system elements [25]. This gives, according to (1), different values of the SCR [13]. To reach a neutral perspective of the future system SCR, here we mediate the two configurations and use an average value of the maximum and minimum short-circuit power, obtained as:
where \(S_{{k{\text{max}}}}^{\prime \prime i}\) is the maximum short-circuit power at the i-th bus-bar; \(S_{{k{\text{min}}}}^{\prime \prime i}\) is the minimum short-circuit power at the i-th bus-bar; \(S_{kAVG}^{\prime \prime i}\) is the average of the maximum and minimum short-circuit power phasors.
From here on, it is decided for simplicity, to refer to the short-circuit power level of a system node \(S_{k}^{\prime \prime i}\) as the average of the maximum and minimum bus-bar short-circuit power, as expressed in (4).
2.3 Optimal planning of synchronous condenser installations
Generally speaking, the goal of optimization is to find the particular set of system variables that maximize or minimize an objective function, subject to a set of constraints.
Quite a number of optimization studies, related to the power system sector, focus on cost minimization of device allocations, such as var planning problems. References [17, 18, 22] investigate the optimal allocation of devices for reactive power support so as to minimize the network losses [17, 18] or the investment cost of these devices [22]. Even though this study focuses on short-circuit power levels, it shares the benefit in common with these studies. The type of device that is meant to be allocated in the system: synchronous condensers, besides additional short-circuit power and inertia, provide reactive power regulation to the system.
Definition and modeling of optimization problems are implemented by defining: objective functions, decision variables and constraints.
2.4 Objective function and decision variables
Based on these considerations, it is therefore decided to model the objective function so as to minimize the cost of synchronous condenser installations. The initial objective function provided in [22] is reported here as (5):
where \(S_{n}^{i}\) is the synchronous condenser rated apparent power to be installed at the \(i\)-th bus-bar; \(C_{F}^{i}\) is the fixed cost of a synchronous condenser installation at the \(i\)-th bus-bar; \(C_{V}^{i}\) is the variable cost of a synchronous condenser installation at the \(i\)-th bus-bar; \(BUS_{i}\) is a flag containing binary elements indicating the allocation of a synchronous condenser installation at the \(i\)-th bus-bar (value equal to 1) or not (value equal to 0); \(N\)is the total number of candidate bus-bars in the system.
The decision variables contained in \(x\)consist of \(S_{n}^{i}\) and \(BUS_{i}\) respectively the rated apparent power and optimal locations for the synchronous condenser installations. Since interest is placed upon the SCR of bus-bars acting as POIs to the static converter-based renewable generation, these nodes are considered as the candidates for synchronous condenser installations as to the relatively small network. Otherwise, the network impedances would have the effect of diminishing the short-circuit power contribution at the POI. This also explains the choice of installing synchronous condensers at the AC nodes of the Skagerrak, Konti-Skan, Kontek and Storbaelt HVDC interconnections in Denmark. Certainly this assumption can be relaxed for larger system optimization.
It is decided to model and simulate the electrical power system in DIgSILENT PowerFactory. This influences the setup of the optimization as follows.
The synchronous condensers are modeled in DIgSILENT PowerFactory as synchronous machines with power-factor equal to zero since no active power is provided by these devices. In order to select in DIgSILENT PowerFactory the machine element type “TypSym”, representing the different types of synchronous condensers available to the TSO, the decision variable related to the synchronous condenser rated apparent power \(S_{n}^{i}\) is tied to an integer decision variable \(Typ^{i}\).
From Table 1, depending on the value assigned to \(Typ^{i}\), the corresponding value of rated apparent power \(S_{n}^{i}\), is assigned to the objective function in (5). Thus the objective function may alternatively be expressed as:
where \(Typ^{i}\)is the type of available synchronous condenser installation that can be allocated at the \(i\)-th bus-bar as shown in Table 1.
The formulation given in (6) is to be used temporarily in the optimization process, in place of (5). The purpose is to use exclusively integer decision variables which work better with the synchronous condenser machine types defined in DIgSILENT PowerFactory and with the binary synchronous condenser allocation flag \(BUS^{i}\). For evaluation of the exact cost of a synchronous condenser, (6) is then changed to (5). The integer decision variable related to the machine type \(Typ^{i}\)is thus converted into its counterpart in \(S_{n}^{i}\) (Table 1), allowing the objective function to calculate the correct total installation cost.
It is clear at this point, that the optimization is of integer type, since both \(Typ^{i}\) and \(BUS_{i}\) contain integers.
2.5 Constraints
The constraints of the optimization problem are modeled as (7):
where \(x_{i} = Typ^{i}\)and \(x_{i + N} = BUS_{i}\); \(P_{n}^{i}\) is the total rated MW of wind generation connected at the \(i\)-th bus; \(n\)is the number of synchronous condenser installations to be added which is the same as the number of system nodes interested by synchronous condenser installations.
In (7), the nonlinear inequality constraints represent the minimum value of the SCR needed to have a strong \(i\)-th bus-bar. The linear inequality constraints limit instead the range of choice of synchronous condenser machine types to those listed in Table 1. Whereas the equality constraint, enforces the number of total synchronous condenser installations in the system equal to the sum of the binary values contained in the synchronous condenser allocation flag \(BUS_{i}\).
3 Methodology
3.1 Genetic algorithm optimization in MATLAB
From (7), it is possible to observe that integer variables and constraints are involved. Moreover, the value of the short-circuit power \(S_{k}^{\prime \prime i}\) is nonlinear with respect to the type of condenser installations at disposal (\(Typ^{i}\)) and the location (\(BUS_{i}\)). GA function of the MATLAB Optimization Toolbox [28] is suitable for mixed-integer nonlinear programming (MINLP) problems. In this specific case, the presence of integer constraints, causes particular settings to be automatically established when running the “GA” solver. These are [29]:
-
1)
Special and fixed mutation, cross-over and creation functions;
-
2)
Fixed population type;
-
3)
No equality constraints.
The last point can though be overcome, as shown in (8) where the equality constraint in (7), expressing the number of synchronous condenser installations \(n\) to be allocated, is expressed as two inequality constraints [29]:
3.2 Short-circuit calculations in DIgSILENT PowerFactory
Nowadays numerous programs are available, performing all kinds of system assessments, including short-circuit studies according to different standards and methodologies. The aim here, is to find the system bus-bars’ average short-circuit power \(S_{k}^{\prime \prime i}\), defined in (4). DIgSILENT PowerFactory calculates automatically three-phase symmetrical short-circuit currents and corresponding short-circuit power levels at the systems’ bus-bars. Based on the IEC 60909 standard, the maximum and minimum short-circuit powers are computed, depending on the values of the voltage factors applied [24].
Based on data from the Danish TSO Energinet.dk, the values of the voltage factor used respectively for the maximum and minimum short-circuit currents are 1.05 for \(c_{\text{MAX}}\) and 0.945 for \(c_{\text{MIN}}\) [30]. Once the short-circuit power \(S_{k}^{\prime \prime i}\)is determined, then the short-circuit ratio \(SCR_{i}\) is computed at the POIs connecting wind-generation to the system using (1).
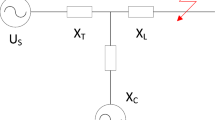
3.3 Synchronous condenser setup in DIgSILENT PowerFactory
The connection of synchronous condensers to the DK1 network in DIgSILENT PowerFactory is modeled as shown in Fig. 1, consisting of a synchronous machine element connected to the 400 kV bus-bar acting as wind farm POI, through a step-up transformer. The positive sequence impedance of the transformer in per-unit is set equal to its short-circuit voltage \(uk\). It is decided for simplicity to set the number of parallel transformers in the DIgSILENT transformer model to n.1. This choice is intended to bring more conservative results, since with n.2 transformers in parallel, the equivalent short-circuit impedance seen at the POI would be lower. Before running the simulations, the breaker element connecting the synchronous condensers to the low-voltage side of the respective transformers is set open as in Fig. 1. During the simulations, the breaker element is closed or open depending upon the values contained in the synchronous condenser allocation flag \(BUS_{i}\). The machine types are chosen among the 170 and 270 MVA units [27] in Table 1.
3.4 Automatic data exchange DIgSILENT PowerFactory- MATLAB
The streamline adopted, shown in Fig. 2, is based upon data exchange between MATLAB-DIgSILENT PowerFactory using the dedicated DIgSILENT PowerFactory module [24], and the acronym SC stands for synchronous condensers. This enables the software to perform calculations through execution of Python scripts using the script presented in [33] as starting point. The exchange of data observes the following procedure:
-
1)
A file, \({\text{x}} . {\text{txt}}\) containing the potential solution associated to the variables \(x_{i} = Typ^{i}\) and \(x_{i + N} = BUS_{i}\), representing the type and the location of the synchronous condenser installations, is generated by MATLAB and read by a Python script;
-
2)
On the basis of the information contained in \({\text{x}} . {\text{txt}}\), Python sends to DIgSILENT PowerFactory, the type and position of the synchronous condenser installations in the system which are then connected;
-
3)
Python tells DIgSILENT PowerFactory to perform short-circuit calculations on each system bus-bar to find the values of maximum and minimum short-circuit power according to the IEC 60909 method;
-
4)
The calculation results are returned in \({\text{DataMax}} . {\text{mat}}\) and \({\text{DataMin}} . {\text{mat}}\) files;
-
5)
MATLAB calculates the average bus short-circuit power \(S_{k}^{\prime \prime i}\) and evaluates the constraints of the optimization problem;
-
6)
The process is repeated for all iterations of the genetic algorithm. For each generation, the \({\text{x}} . {\text{txt}}\) and \(. {\text{mat}}\) files generated after the previous iteration are automatically replaced by new ones containing different values These depend on the type of synchronous condensers connected to the system.
4 Energinet.dk DK1 case study
The proposed approach is tested on the Western Danish transmission system 2012 DK1 model provided by Energinet.dk, modified to emulate a low inertia system. The geographical representation of the DK1 system is better illustrated in Fig. 3. The model does not include the 200 MVA synchronous condenser installation at Fraugde (FGD) [16] and the additional line between Revsning (REV) and Endrup (EDR) substations. The main changes to this original model are the phasing out of all synchronous machines (Table 2). The exceptions are those installed at Tjele (TJE) and Vester-Hassing (VHA) substations, and the isolation of the DK1 grid from its interconnections with DK2, Sweden, Norway and Germany. While HVDC interconnections are currently used to link the DK1 grid to the Nordic system, this is not the case for Germany, which contributes to the short-circuit power through AC interconnections, as shown in Table 3.
The trend for Germany though, resulting from a study of Fraunhofer IWES mentioned in [6], sees the replacement of conventional units with converter-based ones and subsequent decline of short-circuit power levels. Based on this, it is decided to formulate a hypothetical worst-case futuristic scenario, where the German grid is supposed to be dominated by converter-based RES (e.g. wind and PV), to an extent that it will be able to supply a negligible amount of short-circuit power to DK1. The short-circuit power contributions from the external grids shown in Table 3, are therefore disregarded (Table 4).
The total amount of wind power added to the system is based upon TSO future predictions for year 2036, where more than 7 GW of wind generation is installed [16]. From [2, 4], it is possible to observe for the DK1 system that new planned off-shore wind farms are to be located mostly off the Western side of the Jutland peninsula. Therefore new hypothesized wind power installations were added to the system. The locations chosen as POI for the hypothesized future wind farms in the DK1 system are at the 400 kV substations, listed in Table 2. It is decided to concentrate the wind production in large quantities at a few nodes, in order to lower the SCR significantly and avoid excessive computational burden. Wind farms are placed at nodes EDR, FER, IDU, MAL, TRI, which are to be the candidate locations for synchronous condenser installations. In particular, EDR and IDU are considered as weak nodes since they have SCR lower than 3, as shown in Table 5 in the column “n = 0”.
The wind turbine generator contributions to the short-circuit current, calculated using the IEC 60909 method, are set in DIgSILENT PowerFactory to “only maximum short-circuit current contribution” meaning that the contribution to minimum short-circuit current is neglected [35]. The maximum contribution of wind turbine generator short-circuit current is therefore set to 1.1 p.u. [12]. Assuming cosφ = 0.9 for the wind generators, the maximum short-circuit current contribution in kA is calculated as (9):
where \(I_{{k{\text{max}}\_WTG}}^{\prime \prime }\) is the maximum short-circuit current contribution of the single wind turbine generator; \(S_{b\_WTG}\) is the base apparent power of the 8 MW single wind turbine which is assumed 8/0.9 = 8.89 MVA; \(U_{n\_WTG}\) is the nominal line-to-line voltage of the single wind turbine. For the 8 MW turbine this value is at the stator which is 6.6 kV. The quantities in (9) with the subscript “A” are referred to the wind turbines used to model the Anholt wind farm. The values assigned to \(S_{b\_WTG\_A}\) and \(U_{n\_WTG\_A}\) are respectively assumed as 3.6/0.9 = 4 MVA and 0.69 kV.
The synchronous condensers installations are modeled according to the Siemens A/S data [27] in Table 1, along with the step-up transformer in the Appendix A, Table A1. The allocation cost coefficients adopted for the machines, are those for refurbished synchronous condensers in [22]: the fixed cost coefficient \(C_{F}^{i}\) and the variable cost coefficient \(C_{V}^{i}\) in (3)–(4) are set respectively equal to zero and 3 M $ per 100 Mvar.
The MATLAB GA solver is set to a population size of 100 and a stall time limit of half an hour, to speed-up computation. The simulations are conducted on Lenovo Thinkpad X230, 2.9 GHz, core i7 in Windows 7, 32-bit OS. The simulation results respecting the problem constraints were kept. The maximum number of synchronous condensers in the system is considered 10. The results corresponding to the lowest total cost of the installations were selected as the best and final ones. These are organized in Table 4. Imposing a constraint of only one synchronous condenser installation in the system, \(n = 1\) did not satisfy the constraints. Instead from \(n = 2\), the genetic algorithm allocates frequently the correct number of synchronous condenser installations.
The simulation results, in Table 4, show that the genetic algorithm considers nodes EDR and IDU as best for synchronous condenser allocation. This makes sense, as these are the weakest nodes acting as POI for wind generation.
It is also interesting to note that the solutions in Table 4 point exclusively to the installation of the 170 MVA units. This makes sense, since the goal of the optimization process is to reduce the total cost of the installations.
The improvement in POI SCR is shown in Fig. 4 for cases of optimal selection and allocation of respectively 2, 3, 4 synchronous condenser installations in the modified DK1 system with additional wind power. It appears 3 installations, are the minimum necessary to consider all wind farm POIs as sufficiently strong.
As for the average short-circuit power, Fig. 5 shows that the addition of the optimal synchronous condenser installations improves the short-circuit power at all of the system bus-bars, although it remains under the level of the DK1 2020 system at nodes ASR, EDR, FGD, FVO, KAS, KIN, LAG, REV, SVS.
Both the increment in the SCR and the short-circuit power is not so pronounced. This due to the step-up transformer positive sequence reactance, which diminishes the short-circuit power contribution at the high-voltage side of the transformer.
5 Conclusion
An automatic method for allocation of synchronous condensers has been presented in this paper. The approach is based on automatic data exchange between MATLAB and DIgSILENT PowerFactory that compute the main parts of the allocation process: respectively the short-circuit calculations and the device optimization.
The method has been implemented on the 400 kV portion of an exclusively wind power-fed 2012 Western Danish transmission system DK1 with n.5 bus-bars acting as POI to an addition of a rated capacity of 7.4 GW of active power to the system.
The following has been observed:
-
1)
Synchronous condenser allocation is prioritized at nodes with the lowest SCR among the candidate ones;
-
2)
The goal of minimizing the total installation costs is reached by installing exclusively 170 MVA synchronous condenser units;
-
3)
Moreover, the final results give only one installation with two synchronous condensers at EDR which corresponds to the node with the lowest SCR. The remaining installations consist of single machines;
-
4)
Average short-circuit power levels are improved at all system bus-bars considered with respect to the system scenario with no synchronous condensers installed.
The results obtained with the DK1 model here proposed, seem to be conservative. It is thus expected that the SCR could be further improved by addition of additional synchronous condensers and lines, which would increase the SCR and reduce the system impedance. On the other hand, the addition of new HVDC interconnections based on VSC technology, that are able to black-start, e.g. new COBRA HVDC interconnection to the Netherlands, may reduce the need of short-circuit power for operation.
References
Andersson G, Hyttinen M, Sweden ABB (2015) Skagerrak the next generation—HVDC and power electronic technology system development and economics. In: Proceedings of CIGRE, 2015, Lund. https://library.e.abb.com/public/59091e6efb69419dbe1ff4a6f9adac4e/Skagerrak%20The%20The%20Next%20Generation.pdf
Energinet.dk (2014) Energinet.dk’s analysis assumptions 2014–2035. September 2014. Energinet.dk website (2016) http://www.energinet.dk/EN/El/Udvikling-af-elsystemet/Analyseforudsaetninger/Sider/default.aspx
Energinet.dk (2013) Amendment to Energinet.dk’s ancillary services strategy. 06 November 2013. Energinet.dk website (2016). http://energinet.dk/EN/El/Systemydelser-for-el/Sider/Systemydelserforel.aspx
V164-8.0 MW (2016) http://www.4coffshore.com/windfarms/turbine-mhi-vestas-offshore-wind-v164-8.0-mw-tid89.html
Ackermann T (2012) Wind power in power systems. 2nd edn. Wiley, Hansen AD, Chapter 5—generators and power electronics for wind turbines (ISBN 978-0-470-97416-2)
Kubis A, Ruberg S, Rehtanz C (2014) Development of available short-circuit power in Germany from 2011 up to 2033. In: CIRED workshop, Rome, Italy, 11–12 June 2014, 5 pp
Lisias VL Abreu, Shahidehpour M (2006) Wind energy and power system inertia. In: 2006 power engineering society general meeting, Montreal, Quebec, 6 pp
Muljadi E, Gevorgian V, Singh M et al (2012) Understanding inertial and frequency response of wind power plants. In: National Renewable Energy Laboratory Conference paper, NREL/CP-5500-55335. IEEE symposium on power electronics and machines in wind applications, Denver, CO, USA, 16–18 July 2012, 8pp
Muyeen SM, Al-Durra A, Hasanien HM (2013) Modeling and control aspects of wind power systems. Intech, chapters published 20 March 2013 under CC BY 3.0 license. Abo-Khalil AG, Chapter 7—impacts of wind farms on power system stability. http://dx.doi.org/10.5772/55090
Pelletier MA, Phethean ME, Nutt S et al (2012) Grid code requirements for artificial inertia control systems in the New Zealand power system. In: Proceedings of 2012 IEEE power and energy society general meeting, San Diego, CA, USA, 22–26 July 2012, 7 pp
Ulbig A, Rinke T, Chatzivasileiadis S et al (2013) Predictive control for real-time frequency regulation and rotational inertia provision in power systems. In: Proceedings of 52nd IEEE conference on decision and control, Florence, Italy, 10–13 Dec 2013, 8 pp
Roy A (2014) Transmission side protection performance with type-IV wind turbine system integration. In: Proceedings of North American power symposium (NAPS), 7–9 Sept 2014, Pullman, WA, 6pp
Transmission and Distribution Committee of the IEEE Power Engineering Society (1997) IEEE guide for planning DC links terminating at AC locations having low short-circuit capacities. IEEE standard n.1204-1997
Zhang Y, Huang SH, Schmall J et al (2014) Evaluating system strength for large-scale wind power integration. In: Proceedings of IEEE PES general meeting, National Harbor, USA, 27–31 July 2014, 5 pp
Glaninger-Katschnig A (2013) Contribution of synchronous condensers for the energy transition. Elektrotech Inf 130(1):28–32
Abildgaard H, Qin N, Energinet.dk (2015) Synchronous condensers for reliable HVDC operation and bulk power transfer. In: IEEE power and energy society meeting, 5 August 2015
Zhang H, Zhang L, Meng F (1998) Reactive power optimization based on genetic algorithm. In: Proceedings of 1998 international conference on power system technology, Beijing, China, 18–21 August 1998, 6 pp
Kapadia RK, Patel NK (2013) Reactive power optimization using genetic algorithm. In: Proceedings of 2013 Nirma University international conference on engineering (NUiCONE), Ahmedabad, India, 28–30 November 2013, 6 pp
Seifi H, Sepasian MS (2011) Electric power system planning issues, algorithms and solutions. Springer, Berlin. https://doi.org/10.1007/978-3-642-17989-1
Whitley D (1994) A genetic algorithm tutorial. Statistics and computing. Kluwer Academic Publishers, Dordrecht
Abdelaziz AR (2000) Genetic algorithm-based power transmission expansion planning. In: Proceedings of 7th IEEE international conference on electronics, circuits and systems, Jounieh, 17–20 Dec 2000, 4 pp
Hussain Z, Chen Z, Thogersen P et al (2014) Dynamic reactive power compensation of large-scale wind integrated power system. IEEE Trans Power Syst 30(5):2516–2526
Stativa A, Gavrilas M, Stahie V (2012) Optimal tuning and placement of power system stabilizer using particle swarm optimization algorithm. In: Proceedings of international conference and exposition on electrical and power engineering (EPE 2012), Iasi, Romania, 25–27 Oct 2012, 6 pp
DIgSILENT Gmbh (2014) DIgSILENT power factory 15 user manual
IEC (2001) IEC 60909-0, Short-circuit currents in three-phase a.c. systems—Part 0: calculation of currents, 1st edn. http://www.academia.edu/7213550/IEC_60909-0-Short-circuit_currents_in_three-phase_a_c._systems_-_Calculation_of_currents_ENG
Boutsika TN, Papathanassiou SA (2007) Short-circuit calculations in networks with distributed generation. Electr Power Syst Res 78:1181–1191. https://doi.org/10.1016/j.epsr.2007.10.003
Siemens A/S (2015) Synchronous condenser data sheets and one-line diagrams, courtesy of Siemens A/S in data 30 March 2015
The Mathworks website (2015) http://se.mathworks.com/help/gads/ga.html
The Mathworks website (2015) http://se.mathworks.com/help/gads/mixed-integer-optimization.html?s_tid=srchtitle
Energinet.dk (2016) DK1 Short-circuit data 400kV nodes for SCAPP project, courtesy of Energinet.dk in data 31/05/2016
Horns rev 3 offshore wind farm (2016) http://www.4coffshore.com/windfarms/windfarms.aspx?windfarmid=DK19. Accessed 16 Oct 2017
Anholt offshore wind farm(2016)http://www.4coffshore.com/windfarms/anholt-denmark-dk13.html. Accessed 25 Apr 2017
PowerFactory DigSILENT Python Script to load flow (2016) https://gist.github.com/jmmauricio/1198491fa8223572881a
The electrical connections to Norway and Germany extended. https://energinet.dk/Om-nyheder/Nyheder/2017/04/25/Pressemeddelelse-De-elektriske-forbindelser-til-Norge-og-Tyskland
DIgSILENT Gmbh (2016) DIgSILENT power factory technical reference documentation—static generator elmgenstat, edition 1
Siemens 3.6 MW turbine specifications. http://www.4coffshore.com/windfarms/turbine-siemens-swt-3.6-120-tid45.html
Acknowledgements
The authors would like to thank Siemens A/S and Energinet.dk for providing respectively the data of the synchronous condensers and the model of Western Danish transmission system DK1 for year 2012. Special acknowledgement also goes to the DTU Electrical Engineering department, Martin L. Wittrock, Jundi Jia and Angel Perez for their precious support and advice.
Author information
Authors and Affiliations
Corresponding author
Additional information
CrossCheck date: 26 June 2017
Appendix A
Appendix A
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
MARRAZI, E., YANG, G. & WEINREICH-JENSEN, P. Allocation of synchronous condensers for restoration of system short-circuit power. J. Mod. Power Syst. Clean Energy 6, 17–26 (2018). https://doi.org/10.1007/s40565-017-0346-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40565-017-0346-4