Abstract
A fractional frequency transmission system (FFTS) is a promising solution to offshore wind power integration, for which the hexagonal modular multilevel converter (Hexverter) is an attractive choice for power conversion. The Hexverter has recently been proposed to directly connect two three-phase systems of different frequencies and voltage amplitudes, with only six branches in the FFTS in that case. This paper examines for the first time the control scheme of the Hexverter when applied to offshore wind power integration via a FFTS. Firstly, the frequency-decoupled mathematical model of the Hexverter is deduced by introducing the double dq transformation. Then the branch energy of the Hexverter is analyzed in detail and the reactive power constraint equation is obtained. The corresponding control scheme is thoroughly discussed, including the inner loop current control, the outer loop voltage control in both grid-connected mode and passive mode, and a novel optimization method to minimize the circulating current in the Hexverter. Finally, a simulation model of offshore wind power integration via a 4-terminal FFTS based on the Hexverter is built in MATALB/Simulink to verify the feasibility of Hexverter and the effectiveness of the control scheme proposed in this paper.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Offshore wind power is regarded as a promising solution to the worldwide energy crisis, and its integration has attracted much research attention. Because of the large charging current along the submarine cable, conventional 50/60 Hz HVAC transmission technology is restricted to a short transmission distance as well as low transmission efficiency. As for HVDC transmission systems, a high-voltage AC/DC converter station must be built on or under the sea. Besides, DC power conversion and circuit breaker technology is at an early stage of development, inevitably causing high construction cost.
Consequently the fractional frequency transmission system (FFTS) [1,2,3,4], sometimes also called the low frequency alternating current (LFAC) [5,6,7,8] transmission system, provides a new scheme to solve these problems. In the proposed FFTS solution, the offshore wind farm and the offshore transmission system work at a relatively low frequency and connect to the industrial frequency grid via a full-size onshore AC/AC converter. Two main advantages can be expected in this solution: firstly, the charging current is greatly reduced due to the low frequency; secondly, only one onshore AC/AC converter station is required, thus the technical and economic performance can be greatly improved compared to HVDC and HVAC solutions.
As the key equipment for power conversion, the high-voltage high-power AC/AC converter plays the most important role in a FFTS. The modular multilevel matrix converter (M3C) was proposed by Erickson and Al-Naseem in 2001 [9]. It replaces the half-bridge cells of the branch submodules (SMs) in a modular multilevel converter (MMC) with full-bridge cells and can directly connect two three-phase AC systems of different frequencies and voltage amplitudes without a central DC-link. Fundamental research on the M3C has been conducted based on modeling and experimentation [10,11,12,13,14]. The M3C retains the advantages of easy scalability and high power quality that the MMC has due to its modular design. However, the M3C requires 9 branches to achieve power conversion and each branch consists of n SMs; thus, M3C topology has shortcomings of larger volume, higher cost and the potential for lower reliability due to the larger number of components. Moreover, the M3C topology provides many circulating current paths and the suppression strategy for these can be complicated.
Baruschka and Mertens [15] proposed a new three-phase direct AC/AC modular multilevel converter with 6 branches in hexagonal configuration in 2011 and named it the Hexverter. Subsequent studies on the Hexverter mainly focus on its branch energy control based on adjacent compensating power [16,17,18]. Reference [19] presents a simplified qualitative comparison of previously presented cascaded multilevel converter topologies for AC/AC conversion, with particular emphasis on motor drive applications. It draws the conclusion that the back-to-back connected MMC operates best at synchronous speed, whereas the M3C and Hexverter are better suited for low-frequency output. It is also shown in [20] that the Hexverter system offers superior performance for low-frequency wind turbines. Furthermore, compared with back-to-back connected MMC and M3C, only 6 branches are required for the Hexverter to directly connect two three-phase systems; hence, the equipment volume and cost are significantly reduced.
For these reasons, this paper focuses on the control scheme of the Hexverter when applied to offshore wind power integration via FFTS. Firstly, the decoupled mathematical model of the Hexverter is deduced by introducing the double dq transformation in Section 2. Then the branch energy of the Hexverter is analyzed in detail in Section 3 and the reactive power constraint equation is obtained. The corresponding control scheme is thoroughly discussed in Section 4, including the inner loop current control, the outer loop power control in both grid-connected mode and passive mode, and a novel circulating current optimization method. Section 5 describes the construction of a simulation model of offshore wind power integration via a 4-terminal FFTS based on the Hexverter using MATALB/Simulink. This verifies the feasibility of the Hexverter and the effectiveness of the control scheme proposed in this paper.
2 Topology and mathematical model of Hexverter
2.1 Topology of Hexverter
Figure 1 shows the circuit configuration of the Hexverter. It consists of 6 branches and each branch contains n series-connected SMs, an inductor L and an equivalent resistance R. Each SM consists of an IGBT-based single-phase full bridge together with a capacitor as the dc voltage source. The Hexverter connects two three-phase AC systems. As shown in Fig. 1, V u , V v , V w , and i u , i v , i w represent the three-phase voltage and current respectively of the industrial frequency (IF) system (or the source side system) with frequency of f s ; V a , V b , V c , and i a , i b , i c represent the three-phase voltage and current respectively of the fractional frequency (FF) system (or the load side system) with frequency of f l . The branches are named after the terminals they connect, such as branch u-a in Fig. 1. The series-connected SMs in each branch can be considered as controllable voltage sources, represented by V bk , k = 1, 2, …, 6.
2.2 Mathematical model of Hexverter
Define the voltage between the connected systems’ neutral points as V NO and the circulating current as I cir . Applying Kirchhoff’s voltage and current laws to Fig. 1 obtains:
Adding together the equations in (1) cancels many voltage terms, leaving:
where
The following equations can be obtained when the IF system and the FF system are both three-phase three-wire symmetrical AC systems:
Subtracting the last three equations of (1) from the first three equations:
From (1) and (2) we can see that the branch voltage and current are coupled with components of both the IF and the FF systems. Besides, the voltage and current of the 6 branches affect each other through the circuit connection. It’s unmanageable to design the control strategy aiming at only one branch. Thus, in the following derivation, Branches 1, 3, 5 are combined in one group (represented by the subscript “1”), while Bridges 2, 4, 6 are combined in another group (represented by the subscript “2”), then applying the coordinate transformation to the two groups respectively.
The αβ0 transformation matrix of C αβ0 is defined by:
Applying the αβ0 transformation to the three-phase voltage expression of the IF system and the FF system in (1) respectively gives
Throughout this paper, the lowercase letter subscripts of voltage and current are u, v, w, and s for the IF system, and a, b, c, and l for the FF system.
Applying the αβ0 transformation to (3), (4), (6) respectively gives
Replacing the αβ0 components of branch current by the components of the two AC systems’ currents.
where \(c_{1} = \frac{1}{2}\), \(c_{2} = \frac{1}{2\sqrt 3 }\) throughout this paper.
The branch voltage expressions can be obtained by substituting (11) and (12) into (8) and (9).
As shown in (13) and (14), there are two components with different frequencies f s and f l in the branch voltage. To decouple the f s and f l components in the branch voltage, this paper introduces the double dq transformation which transforms both f s and f l components in the branch voltage to their respective dq coordinates.
The double dq transformation matrices are defined by
where ω s and ω l are the angular frequencies of the two AC systems.
For corresponding f s and f l components, pre-multiplying (13) and (14) by C dq_s or C dq_l transforms αβ to dq.
where \(\varvec{A} = \left[ {\begin{array}{*{20}c} {c_{1} } & { - c_{2} } \\ {c_{2} } & {c_{1} } \\ \end{array} } \right],\;\varvec{B} = \left[ {\begin{array}{*{20}c} {c_{2} } & {c_{1} } \\ { - c_{1} } & {c_{2} } \\ \end{array} } \right]\).
The branch zero sequence voltage expression can be obtained from (13) and (14).
This completes the derivation of frequency-decoupled voltage equations for the six branches of the Hexverter in dq0 coordinates.
3 Branch power analysis of Hexverter
Without loss of generality, set the three phase voltage and current of the IF system and the FF system as:
where V sm and I sm are the voltage and current amplitudes of the IF system; V lm and I lm are the voltage and current amplitudes of the FF system; and θ and φ are the initial phase angles between the current and voltage of the systems.
Compared to the whole branch voltage, the voltage drop across the branch resistance R and the inductor L is negligible. Substituting (18) and (19) into (1) and (2), the branch voltage and current can be derived as follows:
Multiplying V bk by i bk yields the branch power, which contains components with specific frequencies as shown in Table A1.
A stable operation of the Hexverter is only possible with no constant term in the branch power as it would lead to a continuous charging or discharging of the SMs’ dc links and this would ultimately lead to a system breakdown. According to the calculation results in “Appendix A”, the constant component in the branch power is
where P s and Q s are the active and reactive power of the IF system; and P l and Q l are the active and reactive power of the FF system.
The first part of (21) describes the active power difference between the two systems and this difference is approximately 0 when the converter power loss is neglected. The second part depends on the systems’ reactive power, and in actual operation, Q s +Q l =0 cannot be guaranteed. Hence, the following constraint must be satisfied:
4 Control scheme of Hexverter system
Figure 2 shows the overview of the control scheme used for the Hexverter system. It is characterized by a hierarchical structure consisting of the following three control processes.
-
1.
Inner loop current control.
-
2.
Outer loop voltage control in both grid-connected mode and passive mode.
-
3.
Circulating current optimization control.
Inner loop current control receives current commands produced by outer loop voltage control and generates the voltage commands for all of the branch SMs. The simulation model in Section 5 applies phase-shift pulse-width modulation (PS-PWM) to communicate the voltage commands. Each of the voltage commands is compared with its corresponding triangular carrier waveform, generating gate signals.
4.1 Inner loop current control
The inner loop current controller is designed as shown in Fig. 3. These current controllers can be easily derived from (16).
4.2 Outer loop voltage control
The outer loop voltage controller in both grid-connected mode and passive mode is shown in Fig. 4.
4.2.1 Grid-connected mode
In the grid-connected mode, the FF side has strong grid support and Hexverter is primarily used to achieve power conversion between the FF side and the IF side. The outer loop voltage control methods of the Hexverter in an FFTS-integrated wind power system are similar to those of the converter station in an HVDC system. Detailed derivation will not be presented here since such methods have been widely used in various devices and can be easily found in other References [21, 22]. Source-side active power control is governed by:
where P s and P * s are the actual and set values, respectively, for the source side system active power.
Source-side voltage control is governed by:
where V s and V * s are the actual and set values for the source side system line voltage RMS.
Load-side DC capacitor average voltage control is governed by:
where V dc and V * dc are the actual and set values for the sum of dc capacitor voltages of n SMs.
Load-side voltage control:
where V l and V * l are the actual and set values for the load side system line RMS voltage .
4.2.2 Passive mode
When offshore wind power is integrated to an industrial grid via a FFTS, it can be considered as a negative load with indeterminate frequency and voltage connected to the FF side of the Hexverter. The Hexverter is used to provide busbar voltage and frequency support. It is difficult to determine the active and reactive power at the FF side of the Hexverter, because the output active power of an offshore wind farm fluctuates with wind speed and the reactive power is influenced by the length of the transmission cable. Hence, the outer loop voltage control method used for grid-connected mode no longer works for the Hexverter in the passive mode.
Outer loop voltage control in the passive mode uses a filter capacitor. The current flow from an offshore wind farm to the grid is shown in Fig. 5. i Fabc is the output current of the offshore wind farm; i Cabc is the current flowing to the filter capacitor; i labc is the current flowing to the Hexverter; u abc is the FF-side voltage of the Hexverter. The following equations can be obtained from Fig. 5:
Pre-multiplying (27) by C αβ0 and C dq_l in sequence yields the expression in dq coordinates:
The outer loop voltage control equations for the FF side of the Hexverter can be obtained from (28):
To maintain the stability of the capacitor voltage of the Hexverter and to ensure sufficient reactive power support, the IF side of the Hexverter uses constant dc capacitor voltage control and constant AC voltage control. Corresponding control equations are based on the control methods used in grid-connected mode.
4.3 Circulating current optimization control
To reduce the power loss in the Hexverter, and to maximize the proportion of effective current flowing through the IGBT and therefore the power transfer capability of the Hexverter, the circulating current I cir should be controlled to its minimum value. Unlike the control schemes presented in [17], a new circulating current optimization method is proposed as follows to minimize I cir .
Combining (10) and (17) with (22) yields the constraint equations for V NO and I cir :
To facilitate tracking control, V NO and I cir are the DC variables in this paper. According to the first equation of (30), when Q s + Q l is equal to 0, the control objectives can be set as V NO = 0 and I cir = 0. However, in most cases in order to meet the voltage regulation and reactive power demand of the IF side and FF side systems, Q s + Q l is not equal to 0. Therefore, I cir can be minimized by setting the absolute value of V NO as its maximum value or, equivalently, setting the absolute value of V bo1+V bo2 as its minimum value, according to the last equation of (30) and with the condition that the Hexverter is not causing over modulation.
As mentioned above, PS-PWM is used in the Hexverter in this paper and the branch voltage modulation index is defined as:
where V bm is the branch voltage amplitude.
There is an amplitude limit for V bo1 and V bo2 to ensure that V bm will not exceed its maximum value, which is denoted V * dc . When the modulation index m is 1, the upper and lower limits of V bo1 and V bo2 are set according to:
where
Substituting the middle two equations of (30) into the first of (33) yields
Hence, the last equation of (30), (32) and (34) constitute a constrained programming problem of a quadratic curve on a plane, and the optimization objective is to minimize the absolute value of V bo1 + V bo2. The optimal branch voltages may be calculated directly as shown in Fig. 6.
5 Simulation verification
5.1 Simulation model
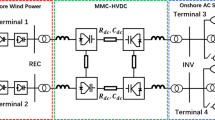
In order to verify the feasibility of applying the Hexverter to offshore wind power integration via FFTS, and the effectiveness of the proposed control scheme in two modes, a simulation model with 4 terminals has been developed, as shown in Fig. 7.
In this model, the offshore wind farm is equivalent to 10 sets of directly driven wind turbines with permanent magnet synchronous generators (PMSG) with a rated power of 2 MW, sending out voltage and current with FF of 50/3 Hz. On the sea is an 8 MW FF load and the 110 kV power grid transmits 10 MW of active power to it through Hexverter 2. The 220 kV power grid guarantees power balance of the FF side through the Hexverter 1. The main parameters of Hexverter 1 and Hexverter 2 are listed in Table 1. To avoid the current of the AC systems and the branch current of the Hexverters being too small, the RMS line voltage of ac systems on both sides of the Hexverters is set as 10 kV by the corresponding transformers. The main parameters of the wind turbines with PMSG are listed in Table 2.
5.2 Simulation waveforms and analysis
5.2.1 Overview of busbar voltage and active power
As shown in Fig. 8, P L is the load power consumption and the value is 8 MW; P W is the wind farm output power; P H1 is the power transmitted from the FF side to the 220 kV grid via Hexverter 1; and P H2 is the power transmitted from the 110 kV grid to the FF side via Hexverter 2 and the value is 10 MW. The real-time wind speed measured from a wind farm in “Appendix B” is used as the simulated wind speed and the simulation waveforms P W and P H1, fluctuate consistently as the wind speed changes. Since Hexverter 1 provides voltage and frequency support, the FF side busbar voltage and frequency are stable at 110 kV and 16.67 Hz respectively. The simulation results have verified the feasibility of applying the Hexverter to offshore wind power integration via a FFTS.
5.2.2 Wind farm performance
As shown in Fig. 9, the wind farm output frequency stabilizes at 16.67 Hz and the converter dc bus voltage of each wind turbine is regulated to the set value of 1200 V. As the wind speed changes, the tip speed ratio fluctuates between 7.7 and 8.3, while the maximum power coefficient is regulated at 0.48. The simulation results indicate that the wind turbines in this FFTS-integrated wind power system based on Hexverters can work in a steady state and respond effectively as the wind speed changes.
5.2.3 Performance of Hexverter
Figures 10 and 11 show a series of simulation waveforms for Hexverter 1 in passive mode and Hexverter 2 in grid-connected mode respectively. From Fig. 10(a)-(b) and Fig. 11(a)-(b), it can be seen that both the IF side and the FF side have good power quality with purely sinusoidal voltage and current in the two modes. Fig. 10(c) and Fig. 11(c) present the voltage of branch u-a of Hexverter 1 and Hexverter 2 respectively, which are multilevel PWM waveforms consisting of components of 50 Hz and 50/3 Hz. The waveforms of Fig. 10(d) and Fig. 11(d) confirm that the branch dc capacitor voltage is well regulated to the set value of 18 kV (3 kV×6). Current tracking of both sides in the two modes is presented in Fig. 10(e)-(f) and Fig. 11(e)-(f). Since Hexverter 1 works in the passive mode and serves to maintain the active power balance, its active currents i sd and i ld fluctuate when the output power of the wind farm changes, whereas both sides of Hexverter 2 have stable current waveforms because Hexverter 2 works in the grid-connected mode. The last simulation waveforms in Fig. 10 and Fig. 11 indicate that the reactive power constraint expressed in (22) is well satisfied through the circulating current optimization control method proposed in Section 4.
6 Conclusion
A fractional frequency transmission system is a promising solution for offshore wind power integration, in the context of the global energy crisis, and the Hexverter is a competitive high-power direct AC/AC converter for FFTS compared to the existing MMC and M3C. This paper is the first presentation of a control scheme for the Hexverter applied to offshore wind power integration via FFTS. A frequency-decoupled mathematical model of the Hexverter is deduced in detail by introducing the double dq transformation. The reactive power constraint equation for the stable operation of Hexverter is determined based on branch energy analysis. The corresponding control scheme is thoroughly discussed, including the inner loop current control, the outer loop power control in both grid-connected mode and passive mode, as well as a novel optimization method to minimize circulating currents in the Hexverter. The feasibility of applying the Hexverter to offshore wind power integration and the effectiveness of the control scheme proposed in this paper are verified by a MATALB/Simulink simulation model of offshore wind power integration via a 4-terminal FFTS based on the Hexverter.
Future research should address low voltage ride-through control and stability analysis of the Hexverter to guarantee the stable operation of this offshore fractional frequency wind power system based on the Hexverter. Since the research results proposed in this paper are confirmed by a simulation model, experimental verification is also left for future work.
References
Wang X, Wang X (1996) Feasibility study of fractional frequency transmission system. IEEE Trans Power Syst 11(2):962–967
Wang X, Cao C, Zhou Z (2006) Experiment on fractional frequency transmission system. IEEE Trans Power Syst 21(1):372–377
Song Z, Wang X, Teng Y et al (2012) Optimal control study for fractional frequency wind power system. In: Proceedings of the 2012 Asia-Pacific power and energy engineering conference (APPEEC), Shanghai, China, 27–29 Mar 2012, 5 pp
Wang X, Wei X, Meng Y (2015) Experiment on grid-connection process of wind turbines in fractional frequency wind power system. IEEE Trans Energy Convert 30(1):22–31
Chen H, Johnson MH, Aliprantis DC (2013) Low-frequency AC transmission for offshore wind power. IEEE Trans Power Deliv 28(4):2236–2244
Miura Y, Mizutani T, Ito M et al (2013) Modular multilevel matrix converter for low frequency AC transmission. In: Proceedings of the 2013 IEEE 10th international conference on power electronics and drive systems (PEDS), Kitakyushu, Japan, 22–25 Apr 2013, pp 1079–1084
Mau CN, Rudion K, Orths A et al (2012) Grid connection of offshore wind farm based DFIG with low frequency AC transmission system. In: Proceedings of the 2012 IEEE power and energy society general meeting, San Diego, CA, USA, 22–26 Jul 2012, 7 pp
Fischer W, Braun R, Erlich I (2012) Low frequency high voltage offshore grid for transmission of renewable power. In: Proceedings of the 2012 3rd IEEE PES innovative smart grid technologies Europe (ISGT Europe), Berlin, Germany, 14–17 Oct 2012, 6 pp
Erickson RW, Al-Naseem OA (2001) A new family of matrix converters. In: Proceedings of the 27th annual conference of the IEEE industrial electronics society, Denver, CO, USA, 29 Nov-2 Dec 2001, pp 1515–1520
Miura Y, Mizutani T, Ito M et al. (2013) A novel space vector control with capacitor voltage balancing for a multilevel modular matrix converter. In: Proceedings of the 2013 IEEE ECCE Asia Downunder, Melbourne, VIC, Australia, 3–6 Jun 2013, pp 442–448
Kammerer F, Kolb J, Braun M (2012) Fully decoupled current control and energy balancing of the modular multilevel matrix converter. In: Proceedings of the 2012 15th international power electronics and motion control conference, Novi Sad, Serbia, 4–6 Sep 2012, pp 3–8
Kawamura W, Akagi H (2012) Control of the modular multilevel cascade converter based on triple-star bridge-cells (MMCC-TSBC) for motor drives. In: Proceedings of the 2012 IEEE energy conversion congress and exposition, Raleigh, NC, USA, 15–20 Sep 2012, pp 3506–3513
Kawamura W, Hagiwara M, Akagi H (2014) Control and experiment of a modular multilevel cascade converter based on triple-star bridge cells. IEEE Trans Ind Appl 50(5):3536–3548
Miura Y, Inubushi K, Ito M et al (2014) Multilevel modular matrix converter for high voltage applications: control, design and experimental characteristics. In: Proceedings of the 40th annual conference of the IEEE industrial electronics society, Dallas, TX, USA, 29 Oct–1 Nov 2014, pp 4690–4696
Baruschka L, Mertens A (2011) A new 3-phase AC/AC modular multilevel converter with six branches in hexagonal configuration. In: Proceedings of the 2011 IEEE energy conversion congress and exposition, Phoenix, AZ, USA, 17–22 Sep 2011, pp 4005–4012
Karwatzki D, Baruschka L, von Hofen M et al (2014) Branch energy control for the modular multilevel direct converter Hexverter. In: Proceedings of the 2014 IEEE energy conversion congress and exposition (ECCE), Pittsburgh, PA, USA, 14–18 Sep 2014, pp 1613–1622
Karwatzki D, Baruschka L, von Hofen M et al (2014) Optimised operation mode for the Hexverter topology based on adjacent compensating power. In: Proceedings of the 2014 IEEE energy conversion congress and exposition (ECCE), Pittsburgh, PA, USA, 14–18 Sep 2014, pp 5399–5406
Karwatzki D, Baruschka L, Mertens A (2015) Survey on the Hexverter topology: a modular multilevel AC/AC converter. In: Proceedings of the 2015 9th international conference on power electronics and ECCE Asia, Seoul, Korea, 1–5 Jun 2015, pp 1075–1082
Ilves K, Bessegato L, Norrga S (2014) Comparison of cascaded multilevel converter topologies for AC/AC conversion. In: Proceedings of the 2014 international power electronics conference, Hiroshima, Japan, 18–21 May 2014, pp 1087–1094
Baruschka L, Mertens A (2013) A new three-phase AC/AC modular multilevel converter with six branches in hexagonal configuration. IEEE Trans Ind Appl 49(3):1400–1410
Bian Z, Xu Z (2016) Fault ride-through capability enhancement strategy for VSC-HVDC systems supplying for passive industrial installations. IEEE Trans Power Deliv 31(4):1673–1682
Li H, Liu C, Li G et al (2017) An enhanced DC voltage droop-control for the VSC-HVDC grid. IEEE Trans Power Syst 32(2):1520–1527
Acknowledgements
This work was supported by a grant from the National Natural Science Foundation of China (No. 51677142) and it is a State Grid Science and Technology Project (No. 52094016000C).
Author information
Authors and Affiliations
Corresponding author
Additional information
CrossCheck date: 16 May 2017
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Meng, Y., Liu, B., Luo, H. et al. Control scheme of hexagonal modular multilevel direct converter for offshore wind power integration via fractional frequency transmission system. J. Mod. Power Syst. Clean Energy 6, 168–180 (2018). https://doi.org/10.1007/s40565-017-0311-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40565-017-0311-2