Abstract
This paper examines the interconnection of two DC microgrids (MGs) with tie-line. The voltages at respective MG buses are controlled to manage the power flow across the tie-line. Formation of such a DC MG cluster ensures higher reliability of power supply and flexibility to manage distributed energy resources and loads in the system. Two MGs consist of photovoltaic and battery units interfaced by power electronic converters. The bus voltages of two DC MGs act as an indicator for the power flow monitoring the supply-demand balance. A decentralized control approach is proposed to control each MG and bus voltage fluctuation in an allowable range. Furthermore, a mode adaptive decentralized control approach is proposed for seamless mode transition in order to assign microgrid operation modes and for the power management of DC MGs. The effectiveness of the proposed concept is validated by simulation and experimental results.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Microgrid (MG) [1,2,3,4] is a conceptual framework for interconnection of distributed generation, energy storages and loads. It has expedited the modernization of existing power systems as an independent entity [5] of the main grid. With its constituents and characteristic of independent operation, it has gained attention to address sustainability, improved reliability and energy efficiency [6] along with ancillary services [7]. MGs can be classified as AC, DC [8] and hybrid AC/DC depending upon the structure, function and objective to be achieved [9, 10].
Rapid growth in the use of renewable energy sources globally has made DC MGs popular as residential loads, energy storage systems (ESS) as well as renewable distributed generators (DGs) like rooftop photovoltaic (PV) are of DC types. However, the intermittent nature of renewable sources like solar PV and wind bring instability issues in MGs and degrades the power quality. Forming an autonomous MG by organizing renewable DGs and ESS can mitigate such power intermittency, thus, enhancing the power quality and making the power supply more efficient [11, 12]. Moreover, the absence of frequency, phase and reactive power control in its operation make DC MG advantageous over traditional AC system. Also, rapid battery charging of electric vehicles can be facilitated by powering through high voltage DC buses [11].
A DC MG is composed of parallel-connected converters interfacing various distributed generation (DG) units. The objectives of DC MG operation are to control the parallel converters involved to interface DG units, and to achieve proportional load sharing and voltage regulation [12]. Control strategies of DC MG are categorized as centralized, decentralized and distributed depending upon the communication link utilized and are discussed in [13,14,15,16] to address the above mentioned control objectives for smooth DC MG operation.
The master slave control and hierarchical secondary control [12, 17] require high bandwidth communication and is only effective when the loads and sources are closely connected. Implementation of power sharing in a droop controlled DC MG is achieved by reducing the voltage reference with an increase in output current [17]. This decentralized control approach without high bandwidth communication compared to master slave control is suitable for DC MG [18]. However, it has the disadvantage of output current sharing accuracy resulted by voltage drop across line impedance [12]. Another disadvantage of droop control is voltage deviation, resulted by the reduction of DC output voltage [19].
The hierarchical control strategy introduced in [14, 17, 20] classifies the control level into primary, secondary and tertiary control in a pyramid shape. The objective of secondary control is to compensate the voltage deviations, as mentioned above, caused by the droop control by setting the compensation reference for primary control. Tertiary control manages the power flow in/out of the MG when it is connected to other MGs or the mains.
DC bus signaling (DBS) and adaptive adjustment of droop gain are the most common type of decentralized control [15]. The details of DBS implementation originally proposed by [21] is given in [15] and [16]. The two main objectives of converters in DC MG operation are to regulate the system voltage deviation and power flow, which may create control conflict since only one operating mode is possible at a time. Thus, the converter units are classified into bus regulating units and terminal regulating units [16] as per their control units. The operating modes are selected on the basis of voltage level for DBS and are classified into grid dominating, storage dominating and utility dominating in [15] and [16] to highlight the DBS principle. Since the frequent charge/discharge might deteriorate the battery, the energy management system (EMS) for battery energy storages should be aware of the battery manufacturers specifications to increase battery lifetime. Overcharge and over discharge can be avoided by using adaptive calculation of droop coefficients to balance state of charge (SOC) between multiple ESS. However, operating mode changes are not accounted.
Renewable intermittency in an islanded DC MG can be addressed by ESS to improve stability and reliability of the system. Moreover, increased reliability can be achieved by interconnecting neighbouring DC MGs to exchange power [22, 23]. Reference [22] has proposed a control strategy for rural grid by interconnecting two DC MGs, operating at different voltage levels, with a bidirectional DC-DC converter to improve energy efficiency and reliability of the system. Reliability and efficiency of the system can also be enhanced by the formation of multiple DC MG clusters interconnecting several identical DC buses through tie-line. However, the system is less stable as DC MG clusters involve multiple parallel converters. Although, various research are conducted in DC MG, the multiple DC MG cluster is still novice in research. Still a lot of research needs to be done in the operation and control of interconnected DC MGs.
This paper proposes a decentralized control approach where the bus voltage of two interconnected MGs are controlled, thus, the power flow through tie- line across MG can be managed. The control strategy is decentralized; hence, the problem of communication stress does not exist. The decentralized control is accompanied by mode change based operation so that the distributed units in MGs can cope up with the bus voltage regulation (BVR) and power flow control, making interconnected MGs autonomous and the power is generated/injected from/into MG when there is the power deficit caused by supply-demand mismatch in a particular MG. The contribution of this paper can be summarized as follows:
-
1)
The use of decentralized control approach eliminates the communication stress when the MG control areas are geographically dispersed.
-
2)
The interconnection of MGs with tie-line facilitates the generation sharing when one of the MGs has supply demand mismatch.
-
3)
Each MG can operate autonomously when there is no deficit in supply and has the provision of generation curtailment during supply surplus.
-
4)
The dynamic operation during load/source variation in MGs has been examined to maintain the bus voltage.
2 Interconnection of DC MGs through tie-line
Tie-line bias control is the mode of automatic generation control for interconnected AC power systems. The functions of tie-line bias control can be classified as [24]:
-
a)
It allows each area to respond to its local load changes.
-
b)
It motivates each area in the cluster to respond to the system frequency change.
-
c)
When an area is unable to supply its demand, unscheduled sharing occurs in the interconnected system. In power systems, areas (microgrids) are interconnected in order to share the generation and load.
In AC systems, load frequency control (LFC) is employed in order to respond to the frequency change of each area, in an interconnected system, and allow the power flow through tie-line as inter-area support [25] during abnormal conditions. The terms “obligation” and “contribution” clarified by [24] for the tie-line bias control refer to the functions a), b) and c) listed above respectively. Several control strategies have been reported for LFC in AC systems [26, 27]. Initially, the LFC was addressed by a centralized control strategy. Such a control strategy carries the drawback of computational burden due to communication links [26, 27] between geographically dispersed control areas. And hence, the idea of decentralized control evolved. In order to achieve the dynamic operation of power systems, decentralization of each cluster control plays a vital role in saving the cost for data communication and reduces the stress for network monitoring [27]. The scope of this paper does not cover the review of control strategies in AC systems.
References [5, 12, 28, 29] and [23] have reported the interconnection of DC MG clusters. Hierarchical control has been proposed in [28, 29] and [23] to regulate the DC bus voltage and adaptive droop based upon the SOC information improves the efficiency of parallel connected batteries in each MGs. Although this distributed approach using low bandwidth communication between neighboring network for the estimated average voltage and SOC of batteries of cluster has been examined by hardware in the loop simulation, the problem of addressing geographically dispersed cluster still exists. Reference [5] proposes tertiary control for power sharing among microgrids in a cluster and each microgrid has communication network communion to the secondary control. Reference [12] proposes a decentralized approach in individual DC MG which modifies effective droop gain for good voltage regulation and load sharing. It shows better performance in comparison with conventional droop control and hierarchical secondary control. However, the tie-line power flow control for interconnected MGs is still centralized. No source sharing has been examined. Though all these literature have significant contribution within the scope of the papers, the interconnection of DC microgrids along with voltage regulation and power flow is still an open research. In DC microgrids, tie-line bias control is achieved by regulating the DC bus voltage to a specific level and provision of power flow between the control areas when an area is unable to respond to its demand during disturbance such that the “obligation” function b) and “contribution” function of tie-line bias control is achieved. The construction of an autonomous DC MG makes a MG able to respond to its local load change. Sections 3 and 4 further explain these functions of two interconnected DC MGs with tie-line.
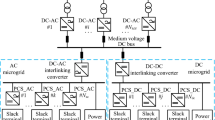
The general configuration for interconnection of DC MGs through tie-line is shown in Fig. 1. Two neighboring DC MGs in remote areas operating at the same voltage level have been considered in this paper for the reliable power supply to the load. The interconnected MGs consist of PV interfaced to each DC bus by means of a DC/ DC boost converter. Battery along with a bi-directional DC-DC converter forms ESS in each MG.
The output voltage for conventional V-I droop control in terms of virtual output impedance can be expressed as (1) [17]:
where v and i are the static terminal voltage and current of the converter respectively; \(V_{ref}\) is the global voltage reference; \({R_{droop}}\) is the equivalent resistance of the converter, affiliated to the droop rate [30]. All the buses in the DC MG cluster obey the droop control in (1). Assuming there are n buses in the DC MG cluster and applying Kirchhoff’s current law, the current flowing from \(i^{\text {th}}\) bus to (\(n-1\)) buses can be expressed as (2) [31]. The power injected through tie-line from the \(i^{\text {th}}\) bus can be represented by (3). Power loss in tie-line is expressed as (4). The power balance of the \(i^{\text {th}}\) MG during tie-line power flow is represented by (5):
where \(V_{dc,i}\) and \(V_{dc,j}\) are the respective DC bus voltages of \(i^{\text {th}}\) and \(j^{\text {th}}\) bus; \(Y_{tie,ij}\), \(Z_{tie,ij}\), \(P_{tie,i}\) are the tie-line admittance, impedance and tie-line power flow respectively; \(P_{G,i}\) and \(P_{D,i}\) are the total generation and demand on \(i^{\text {th}}\) MG. Only two MGs (MG1 and MG2) have been considered for the study in this paper. MG1 and MG2 shown in Fig. 1 operate autonomously unless there is power deficit in one of the MGs.
3 Control strategy
Most converters act as inherent current source converters [16]. Reference current (\(i_{ref}\)) for the current control loop of the converter can be generated from (1). The transfer function (\(G_{conv,i}(s)\)) for inner closed loop current control in \(i^{\text {th}}\) converter in both MGs has low pass characteristic with high bandwidth due to fast switching [16] and is expressed as in (6), where \({\tau _{i}}\) represents time constant. This transfer function yields the bus current (\(i_{busi}\)) at the output [16].
The converters involved in DC MG regulate the power flow of local terminal and the voltage deviation of the system. To avoid control conflict, converters are classified as terminal regulating unit and bus regulating unit for power flow control as per their objective.
The renewable DGs performing on MPPT are termed as terminal regulating unit and their function is to supply the power demand of the system. The power production is independent of DC bus voltage variation. Unlike the PV converter, the battery converter in DC MG regulates the system voltage and nurtures power balance of the system. Because of such an objective, it is termed as bus regulating unit and can be expressed as a thevenin equivalent circuit with series impedance. The thevenin voltage source refers to the voltage reference, the series impedance refers to virtual impedance and the unit control operates in droop control mode [15]. The control loops for the battery converters in two interconnected MGs are shown in Fig. 2. The red dotted indication shows a control loop which generates the voltage error signal of MG1 and MG2 buses. These error signals are the voltage correction term \(V_{err\_1}\) and \(V_{err\_2}\) that restore the voltages at MG1 and MG2 buses and are added to the droop control unit of each MG. The principle behind the bus voltage error minimization indicated in Fig. 2 is expressed as in (7) and can be elaborated as (8) and (9) for MG1 and MG2 respectively, where \(v_{dc1}, v_{dc2}\) represent the dc bus voltages of MG1 and MG2 respectively and \(v_{MG}^*\) signifies the MG reference voltage. \(R_{dp1}\) and \(R_{dp2}\) represent droop gains of battery converters in MG1 and MG2 respectively. \(I_{tie}\) and \(Z_{tie}\) stand for tie-line current and impedance, respectively. \(C_{bus1}\), \(C_{bus2}\) and \(R_{L1}\), \(R_{L2}\) in Fig. 2 represent bus capacitors and load resistances for MG1 and MG1 respectively [23]. The generalized expressions for the battery converter output voltages for MG1 and MG2 can be simplified as in (10) and (11). The tie-line voltage drop \(v_{tie}\) is expressed as (12).
The tie-line power flow is dependent on the voltage difference between two buses and is calculated based upon (3). The amount of tie-line power flow depends upon \(\pm 5\%\) change in the DC bus voltages of interconnected MGs. The rating of tie-line is based upon the maximum temperature of the conductor at which the line is designed to operate. There is always a time delay between a sudden change in thermal heating of conductors to the following temperature rise as the conductors have significant thermal mass. A tie-line can withstand 115% overload for 10 minutes without exceeding design temperature [32].
When a DC current is flowing through round cylindrical conductor the current is uniformly distributed over its cross sectional area and its DC resistance is calculated as (13) [33]. Resistance of \(Z_{tie}\) depends upon the resistivity (\(\rho\)) of a conductive material, its length (l) and cross-sectional area (A) of a conductor. The resistivity of a conductor and temperature coefficient depend upon conductor material. No change in effective resistance due to skin effect and frequency change takes place in DC systems.
The control strategy proposed above is based upon (7) and is only applicable to minimize the bus voltage errors of two MGs. Due to this limitation, the topology for n bus MGs connected with multiple tie-lines and the impact of \(Z_{tie}\) variation in the system have not been considered in this paper.
4 Mode adaptive decentralized control
As mentioned in the control strategy section, the converters in DC MG are categorized into terminal regulating unit and bus regulating unit and each converter has a particular function, either to regulate bus voltage or to regulate the power flow in the local terminal, assigned in order to avoid control conflict. Since the renewable DGs and loads are intermittent in nature, it is necessary to adaptively adjust the operation modes considering such variations. For instance, renewable generators like PV and wind work at MPPT when the load demand is high but this is not similar when the demand is low. To mitigate this issue, the operation modes of DGs and ESS involved in MG are designated depending upon the voltage level.
The DC bus voltage level is classified into three regions: nominal voltage, \(V_{high}\) and \(V_{low}\) as shown in Fig. 3 [16, 30]. \(V_{high}\) and \(V_{low}\) are designated as \(\pm 5\%\) of the nominal DC bus voltage in order to indicate the operation modes designation. Droop and constant power (CP) operations indicated in Fig. 3 account for BVR and constant power mode respectively. For instance, in case of power interruption of renewable:
DG like PV or due to the rise in local consumption in MG1, the DC bus voltage at MG1 decreases and due to the bus voltage deviation between two MGs, power flow from MG2 to MG1 takes place. ESS in both MGs operate in BVR mode. When the local load demand at one MG or both MGs is less than the total generation in each MG, the DC bus voltage increases. In order to retain this increment to the nominal value, the terminal regulating unit such as PV should change its operation from MPPT to BVR mode and battery converter shifts to current control mode and charge/discharge of the battery is determined by the reference current provided to the battery converter (i.e. rated charging current provided by the manufacturer). If the local generation is sufficient to meet the local demand, there is no mode change, terminal regulating unit works on MPPT mode and bus regulating unit on BVR mode. In such manner, the distributed generation units in two MGs switch their operation modes, in order to respond to the supply-demand change, maintaining DC bus voltage. If the generation units and capacity of an energy storage in both MGs are insufficient to satisfy the local demand, load curtailment should be considered in such a case. The details of the generation and energy storage status for such a scenario have been tabulated in first row of Table 1. When the DC bus voltage of a MG decreases further due to the excess demand, the power flows through tie-line due to the difference in bus voltages of two MGs but within the capacity of tie-line.
Contrary to the centralized and distributed control implemented for interconnection of DC MGs with tie-line, the decentralized control proposed in this paper is preferable because it eliminates the communication stress for geographically dispersed control areas. The control implemented qualitatively proves to be simple and feasible. Moreover, the decentralized mode adaptive control for the power management of DC MGs adjusts the operation modes of RES and ESS as discussed above. Such self-disciplined regulation of converters in MGs without communication links enhances the flexibility and reliability of the system.
5 Simulation and experimental results
5.1 Simulation results
Two MGs consisting of PV and battery are built in the piecewise linear electrical circuit simulation (PLECS) environment to validate the above mentioned control strategies. The DC bus voltage is set to be \(380\,\text {V}\). The use of decentralized control is tested for two types of load: constant power load (CPL) and a step load change in each MG to examine whether the load change is self-sustained by the respective MG.
Figure 4 shows the implementation of proposed control loop in Fig. 2. Before \(t=4\,\text {s}\), the voltage difference (\(\mathrm {\Delta } V\)) of MG1 and MG2 is \(0.724\,\text {V}\) and power flows through tie-line (\(P_{tie}=249.8\,\text {W}\)) due to CPL of \(1000\,\text {W}\) and \(1500\,\text {W}\) connected to MG1 and MG2 respectively. \(I_{tie}\) signifies the corresponding tie-line current in Fig. 4. This phenomenon proves the necessity of control loop for bus voltage error minimization in Fig. 2 for the autonomous operation of each MG when the local supply is sufficient to cater the local demand. After the control loop for bus voltage error minimization is activated in \(4\,\text {s}\), the tie-line power flow is reduced to zero by maintaining bus voltages at \(380\,\text {V}\) achieving the function b) discussed in Sect. 2.
A step load is introduced in the system with the proposed decentralized control at \(t= 5\,\text {s}\) and \(10\,\text {s}\) in MG1 and MG2 respectively in Fig. 5. From the waveforms, it can be seen that at steady state, both the DC bus voltages of MG1 (\(V_{dc1}\)) and MG2 (\(V_{dc2}\)) are 380V and hence the tie-line current is zero. At \(t=5\,\text {s}\), there is a step load change in MG1 which causes the power demand to increase. Since PV at both MGs are in MPPT mode, the battery responds to the power deficit caused by load change. The response of battery to the load change regulates the bus voltage fluctuation and it is maintained to be \(380\,\text {V}\), making tie-line current flow to zero. Similarly, at \(t=10\,\text {s}\), a step load is applied to MG2 and MG2 is able to regulate the bus voltage fluctuation and supply power to maintain generation-demand balance. This shows that the MG is able to cater its local demand and hence the “obligation” function a) of tie-line bias control discussed in Sect. 2 is achieved.
The logic behind the relationship between bus voltage increment/decrement due to the change in generation/demand is provided in Sect. 4. For the sake of brevity, CPL of \(200\,\text {W}\) which is less than MPPT generation of PV is provided in both MGs. The changes in MG1 have been observed to validate mode change based operation setting \(V_{high}\) as \(390\,\text {V}\) and \(V_{low}\) as \(370\,\text {V}\) and the bus voltages of MG1 and MG2 along with tie-line current flow are shown in Fig. 6. A DC bus signal of \(395\,\text {V}\) is provided at \(t=0\,\text {s}\) in the control logic, PV at this moment operates at BVR (Fig. 7) and battery is charged with manufacturer’s charging current reference. At \(5\,\text {s}\), the DC bus voltage is ramped from 395 to 380 V (slope \(-5\) per second). When the control logic finds the moment of \(390\,\text {V}\) at \(t=6\,\text {s}\) in Fig. 6, the PV and battery converters are changed to MPPT (Fig. 7) and BVR mode respectively. Similarly, a ramped DC signal from 380 to 365 V has been observed in simulation. The power generation, state of ESS and mode changes in both MGs have been tabulated in Table 1. The first two rows in Table 1 indicate two extreme scenarios of operation when load and generation curtailment respectively should be done. The tie-line current which is the “contribution” discussed in previous section, can be calculated using (2) and its maximum value can be obtained by substituting \(V_{high}\) and \(V_{low}\) in place of bus voltages of \(i^\text {th}\) and \(j^\text {th}\) microgrid in (2). The nominal system parameters used during simulation and experiment are listed in Table 2.
5.2 Experimental results
In this section, a prototype of a droop controlled two interconnected DC MGs with implementation of control strategy discussed in Sect. 3 is established. The experimental platform consists of PV, battery and local load for each MG. The nominal system parameters are listed in Table 2. The DC bus voltage of the two MGs is set to be 48 V, which is generally implemented in telecommunication applications. Each microgrid consists of PV and lead acid battery interfaced to the DC bus by means of a DC-DC boost converter and a bi-directional DC-DC converter respectively. The system was controlled by a dSPACE DS1103 PPC controller board. Four experimental cases have been carried out to validate the interconnection of DC microgrids through tie-line.
5.2.1 Voltage stability test by step load change in the system
This test demonstrates the self-sustained operation of DC MGs connected through tie-line when the generation of a MG is sufficient to supply the demand. The battery currents and DC bus voltages of both MGs during step load change in MG2 are shown in Fig. 8. Figure 9 shows the tie-line current flow during step load change in MG2. It can be seen from Fig. 8 that the corresponding battery of MG2 (\(I_{bat2}\)) responds to the demand while the battery current at MG1 (\(I_{bat1}\)) remains unchanged. The DC bus voltages of both MGs are shown in both Figs. 8 and 9 and are well regulated.
5.2.2 Voltage stability test by generation fluctuation
This experiment aims to verify the voltage stability under proposed control scheme. To emulate the generation fluctuation, an oscillating current is injected by the PV converter in MG1. The bus voltages and PV converter currents for MG1 and MG2 are demonstrated in Fig. 10 and the corresponding battery currents for MG1 and MG2 along with bus voltages are displayed in Fig. 11. It can be seen from the waveforms that the bus voltage is well regulated since the power deficit is compensated by battery in MG1. The PV and battery waveforms in MG2 is unaffected by this variation.
5.2.3 Mode transition test
In this case, MG1 initially operates in generation dominating mode PV being at MPPT mode of operation. The battery is being charged at this time since the renewable generation is sufficient to cater to the load demand. When the battery reaches the saturation point, the bus voltage rises. In such a case, the PV generation working on MPPT is supposed to switch to bus regulation mode in order to curtail the generation. A mode change logic is provided in MG1 and is demonstrated in Fig. 12. The waveform shows that the PV unit goes to bus regulation mode while the battery discharges for the system losses. The control strategy is effective to regulate the bus voltages.
5.2.4 Tie-line power flow test
The change in the bus voltage is realized at MG1, leading to tie-line current flow to MG2 as expressed in (2). Both MG1 and MG2 have a load of 60 \(\mathrm {\Omega }\). It can be seen from Fig. 13 that the tie-line current of 800 \(\text {mA}\) flows from the higher voltage (MG1) to the lower voltage level (MG2). MG1 provides tie-line current while supplying local demand whereas MG2 supplies local demand only. The bus voltages and battery currents of both MGs are shown in Fig. 14.
6 Conclusion
In this paper, the interconnection of two DC MGs through tie-line is implemented for enhancing the reliability and source sharing during power surplus/deficit in a MG. A decentralized control has been proposed focusing on geographically dispersed clusters to provide resilience to the system. The control strategy acknowledges the BVR in each DC MG. The proposed control strategy has been facilitated by mode adaptive control which designates the operation modes of different DG units to venture autonomous operation in MGs. As a result, both system reliability and flexibility could be enhanced. System performance is verified through simulation and experimental results.
References
Lasseter RH (2002) MicroGrids. In: Power engineering society winter meeting, 2002. IEEE, vol 1. New York City, New York, USA, pp 305–308
Lasseter RH (2011) Smart distribution: coupled microgrids. Proc IEEE 99(6):1074–1082
Lasseter RH, Paigi P (2004) Microgrid : a conceptual solution. In: Power electronics specialists conference, PESC ’04. IEEE, Aachen, Germany, pp 4285–4290
Nikkhajoei H, Lasseter RH (2009) Distributed generation interface to the CERTS microgrid. IEEE Trans Power Deliv 24(3):1598–1608
Moayedi S, Davoudi A (2016) Distributed tertiary control of DC microgrid clusters. IEEE Trans Power Electron 31(2):1717–1733
Zubieta LE (2016) Are microgrids the future of energy?: DC microgrids from concept to demonstration to deployment. IEEE Electrification Mag 4(2):37–44. doi:10.1109/MELE.2016.2544238
Beer S, Gómez T, Member S, Dallinger D, Momber I, Marnay C, Stadler M, Lai J (2012) An economic analysis of used electric vehicle batteries integrated into commercial building microgrids. IEEE Trans Smart Grid 3(1):517–525
Wang Z, Wu W, Zhang B (2016) A distributed control method with minimum generation cost for DC microgrids. IEEE Trans Energy Convers 31(4):1462–1470
Liu X, Wang P, Loh PC (2011) A hybrid AC/DC micro-grid and its coordination control. IEEE Trans Smart Grid 2(2):278–286
Loh PC, Li D, Chai YK, Blaabjerg F (2013) Autonomous operation of hybrid microgrid with ac and dc subgrids. IEEE Trans Power Electron 28(5):2214–2223. doi:10.1109/TPEL.2012.2214792
Adhikari S, Tang Y, Wang P (2016) Secondary control for dc microgrids: a review. In: Asian conference on energy, power and transportation electrification (ACEPT). IEEE, Singapore, Singapore, pp 1–6
Tah A, Das D (2016) An enhanced droop control method for accurate load sharing and voltage improvement of isolated and interconnected DC microgrids. IEEE Trans Sustain Energy 7(3):1194–1204. doi:10.1109/TSTE.2016.2535264
Khorsandi Amir, Ashourloo Mojtaba, Mokhtari Hossein (2014) A decentralized control method for a low-voltage DC microgrid. IEEE Trans Energy Convers 29(4):793–801
Chi J, Wang P, Xiao J, Tang Y, Choo FH (2014) Implementation of hierarchical control in DC microgrids. IEEE Trans Ind Electron 61(8):4032–4042. doi:10.1109/ICIEA.2014.6931231
Dragicevic T, Lu X, Vasquez J, Guerrero J (2016) DC microgrids—part I: a review of control strategies and stabilization techniques. IEEE Trans Power Electron 31(7):4876–4891. doi:10.1109/TPEL.2015.2478859
Gu Y, Xiang X, Li W, He X (2014) Mode-adaptive decentralized control for renewable DC microgrid with enhanced reliability and flexibility. IEEE Trans Power Electron 29(9):5072–5080. doi:10.1109/TPEL.2013.2294204
Guerrero JM, Vasquez JC, Matas J, de Vicuna LG, Castilla M (2011) Hierarchical control of droop-controlled AC and DC microgrids—a general approach toward standardization. IEEE Trans Ind Electron 58(1):158–172. doi:10.1109/TIE.2010.2066534
Wang P, Lu X, Yang X, Wang W, Xu D (2016) An improved distributed secondary control method for DC microgrids with enhanced dynamic current sharing performance. IEEE Trans Power Electron 31(9):6658–6673. doi:10.1109/TPEL.2015.2499310
Lu X, Guerrero JM, Sun K, Vasquez JC (2014) An improved droop control method for dc microgrids based on low bandwidth communication with dc bus voltage restoration and enhanced current sharing accuracy. IEEE Trans Power Electron 29(4):1800–1812. doi:10.1109/TPEL.2013.2266419
Guerrero JM, Chandorkar M, Lee TL, Loh PC (2013) Advanced control architectures for intelligent microgrids part I : decentralized and hierarchical control. IEEE Trans Ind Electron 60(4):1254–1262
Schonberger J, Duke R, Round SD (2006) DC-bus signaling: a distributed control strategy for a hybrid renewable nanogrid. IEEE Trans Ind Electron 53(5):1453–1460. doi:10.1109/TIE.2006.882012
Kumar M, Srivastava SC, Singh SN, Ramamoorty M (2015) Development of a control strategy for interconnection of islanded direct current microgrids. IET Renew Power Gener 9(3):284–296. doi:10.1049/iet-rpg.2013.0375
Shafiee Q, Dragicevic T, Vasquez JC, Guerrero JM (2014) Hierarchical control for multiple DC-microgrids clusters. IEEE Trans Energy Convers 29(4):922–933
Cohn N (1957) Some aspects of tie-line bias control on interconnected power systems. Transactions of the American institute of electrical engineers. Part III: power apparatus and systems, pp 1415–1436
Ray PK, Mohanty SR, Kishor N (2010) SmallSignal analysis of autonomous hybrid distributed generation systems in presence of ultracapacitor and tieline operation. J Electr Eng 61(4):205–214. doi:10.2478/v10187-010-0029-0
Pandey SK, Mohanty SR, Kishor N (2013) A literature survey on load frequency control for conventional and distribution generation power systems. Renew Sustain Energy Rev 25(September):318–334. doi:10.1016/j.rser.2013.04.029
Shayeghi H, Shayanfar HA, Jalili A (2009) Load frequency control strategies: a state-of-the-art survey for the researcher. Energy Convers Manag 50(2):344–353. doi:10.1016/j.enconman.2008.09.014
Shafiee Q, Dragicevic T, Vasquez JC, Guerrero JM (2014) Hierarchical control for multiple DC-Microgrids Clusters. In: Systems, signals and devices (SSD). IEEE, Barcelona, Spain, pp 1–6
Shafiee Q, Dragicevic T, Vasquez JC, Guerrero JM (2014) Modeling, stability analysis and active stabilization of multiple DC-microgrid clusters. In: ENERGYCON. IEEE, Cavtat, Croatia, pp 1284–1290
Gu Y, Li W, He X (2015) Frequency-coordinating virtual impedance for autonomous power management of DC microgrid. IEEE Trans Power Electron 30(4):2328–2337
Li C, Chaudhary SK, Savaghebi M, Vasquez JC, Guerrero JM (2016) Power flow analysis for low-voltage AC and DC microgrids considering droop control and virtual impedance. IEEE Trans Smart Grid PP(99):1–11. doi:10.1109/TSG.2016.2537402
NERC: Transmission relay loadability. http://www.nerc.com/files/prc-023-1.pdf
Reta-Hernandez M Transmission line parameters. http://www.unioviedo.es/pcasielles/uploads/proyect-antes/cosas_lineas.pdf
Author information
Authors and Affiliations
Corresponding author
Additional information
CrossCheck date: 14 June 2017
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
ADHIKARI, S., XU, Q., TANG, Y. et al. Decentralized control of two DC microgrids interconnected with tie-line. J. Mod. Power Syst. Clean Energy 5, 599–608 (2017). https://doi.org/10.1007/s40565-017-0306-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40565-017-0306-z