Abstract
The increasing integration of variable wind generation has aggravated the imbalance between electricity supply and demand. Power-to-hydrogen (P2H) is a promising solution to balance supply and demand in a variable power grid, in which excess wind power is converted into hydrogen via electrolysis and stored for later use. In this study, an energy hub (EH) with both a P2H facility (electrolyzer) and a gas-to-power (G2P) facility (hydrogen gas turbine) is proposed to accommodate a high penetration of wind power. The EH is modeled and integrated into a security-constrained unit commitment (SCUC) problem, and this optimization problem is solved by a mixed-integer linear programming (MILP) method with the Benders decomposition technique. Case studies are presented to validate the proposed model and elaborate on the technological potential of integrating P2H into a power system with a high level of wind penetration (HWP).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Concerns over climate change [1, 2] and sustainability have led to a global push towards the proliferation of renewable energy in electricity generation [3]. Accordingly, the integration of wind power generation has grown substantially in recent years. However, the significant increase in the volatile supply of energy has challenged the balance of electricity and required greater ramping capabilities [4]. Therefore, various energy storage devices [5, 6] and carriers [7, 8] such as electric vehicles [9, 10], batteries [11], compressed air [12] and pumped-hydro storage [13, 14] are expected to assist balancing in power systems. Power-to-hydrogen (P2H) is considered to be a promising alternative for this application.
P2H is a technological concept that can convert the surplus electrical energy into a gaseous energy carrier, typically, hydrogen [15] by electrolysis. An important distinction between P2H and other storage technologies is that P2H allows the conversion of energy amongst a variety of energy sectors and end-users [16]. P2H processes include conversion and later use in non-electrical forms. This characteristic is critical for decoupling the production and the consumption of electricity [17]. An increasing number of P2H pilot plants [18], which produce hydrogen from variable renewable power [19–21], illustrate significant potentials for utilizing P2H as energy storage [22–24].
Furthermore, the fast response capability of hydrogen electrolyzers [25] enables P2H to participate in ancillary services [26] for power grids. The provision of ancillary services offers additional revenues for enhancing the P2H value proposition as a storage device. In [27], the authors assessed the potential for P2H to increase wind power dispatchability, and in [28] they explored how to integrate P2H into power systems for load balancing.
Initial results from these analyses illustrate potentially compelling cases for P2H applications. In order to better study the integration of P2H in the power system, an energy hub (EH) [29, 30] equipped with a P2H facility (electrolyzer) and a gas-to-power (G2P) facility (hydrogen gas turbine) is proposed in this paper to accommodate the volatility introduced by a large wind power penetration. The proposed EH stores surplus wind power as hydrogen via P2H. When needed, the G2P facility feeds the energy back to the power grid. Unlike other MW-size energy storage facilities, the EH can not only feed energy back to the power grid, but also directly supply hydrogen products to other industry sectors. This could allow additional wind generation capacity to be installed inside the EH and enhance its economic viability.
The main contributions of our approach include: the P2H and G2P facilities are uniformly modeled in a simplified EH; the EH is integrated into a day-head security-constrained unit commitment (SCUC) formulation with volatile wind power generation; and the economic and technical potentials of EH to accommodate a large wind power penetration is demonstrated by a series of numerical analyses. In general, the proposed problem focuses on the day-ahead optimal scheduling of stochastic power systems with the integration of P2H processing and wind power generation. A mixed-integer linear programming (MILP) approach [31] with the Benders decomposition technology [32, 33] solves the proposed scheduling problem. To consider the uncertainty of wind generation, the Monte Carlo method generates scenarios representing the volatility of wind power.
2 System description and mathematical modeling
2.1 System description
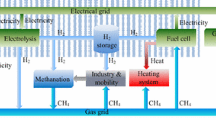
The schematic of a typical P2H facility is given in Fig. 1. The gray part is an EH which composes P2H (electrolyzer), G2P (hydrogen turbine) and hydrogen storage serving as a buffer.
Figure 2 shows the integration principle. P2H is used during periods of surplus wind generation. The surplus wind power that is subject to curtailment is converted into hydrogen by electrolysis and stored. During periods of low wind power generation and high power demand, the energy stored in hydrogen will be converted to electricity by G2P. Small amounts of hydrogen, i.e., MWh-scale, can be stored in high-pressure tanks. Huge amounts of hydrogen, i.e., GWh-scale, can be stored in human-made underground salt caverns. In this way, even balancing seasonal wind energy variations is possible [24].
Providing hydrogen products will reduce the requirement for storage capacity and flexibility to manage the variability of renewable energy. In the long run, the total energy produced by P2H can be much larger than that consumed by G2P and the produced hydrogen can directly serve various industrial applications, i.e., feedstock for the chemical industry, fuel for fuel cell cars or blending with natural gas in natural gas pipelines. Therefore, unlike compressed air energy storage [12] and pumped-hydro storage [13], there is no strict balancing constraint for equating electricity input and output in the EH. In addition to providing bulk energy storage, the flexibility of the electrolyzer and the hydrogen gas turbine also enables EH to provide ancillary services for the power grid.
Since we mainly focus on the integration of the proposed EH into the power grid, specific processes to produce, store and utilize hydrogen are not discussed. We define the EH parameters with reference to previous works. Owing to its fast response to wind fluctuations [15], polymer electrolyte membrane electrolysis [25] is adopted as a suitable process for the P2H facility. Hydrogen gas turbines [28], which start faster and have a higher ramping rate than traditional power plants, are adopted as an example for the G2P facility. Such facilities [18] have been proved to be able to provide both energy balancing and ancillary services, and the optimal capacity ratio between electrolysis and gas turbines is determined using an economic evaluation in [28].
2.2 Mathematical model of economic dispatch
2.2.1 Objective function
The SCUC problem with wind power generation [33] and the proposed EH is formulated as an optimization problem. The objective function (1) consists of fuel costs for generating electricity and P2H and startup costs for the thermal units. The operating costs of wind generating units are assumed to be zero.
where t, i and j are indices of hours, thermal units and EH units, respectively, while N T, N G and N E are the total numbers of hours, thermal units and EH units; F i and F j are production cost functions; I it is commitment state; S it is a constant startup cost, for simplicity; and P it and P jt are output power from thermal units and EH units, respectively.
The quadratic fuel cost function (2) is adopted:
where a i , b i and c i are fuel consumption characteristic coefficients for unit i; and γ i is the fuel price coefficient. And F j will be given in the next part.
In this paper, the convex nonlinear production cost functions in (2) are approximated by a set of piecewise linear blocks using the method applied in [34]. Thus (2) is approximated by (3) with constraints (4) and (5):
where c ik is the incremental fuel cost of unit i for segment k; p ikt is the generation of unit i at hour t for segment k; p ik,max is the maximum capacity of unit i for segment k; and N i is the total number of segments for unit i.
2.2.2 Constraints for P2H and G2P in an EH
Three working modes of EH including P2H, G2P and idling are considered. In P2H mode, the hub acts as a load, and in G2P mode, it is a generator. While in the idling mode, the hub is on standby for either P2H or G2P. Accordingly, the following integer variables and constraints are introduced for EH unit j at hour t:
where \(I_{jt}^{\text{G2P}}\) is 1 in the G2P mode, otherwise it is 0; \(I_{jt}^{\text{P2H}}\) is 1 in the P2H mode, otherwise it is 0.
Superscripts G2P and P2H are used throughout the following formulation. Integrating the EH in SCUC, F j is defined as in (7):
To simplify, when the EH works in the G2P mode, the G2P facility [35] is assumed to have the same cost characteristics as those of a traditional gas turbine, following the quadratic model of (2), with a self-produced hydrogen fuel; when it works in the P2H mode, its cost is defined as in (8) [36]:
where the EH output is negative corresponding to the P2H mode. In the SCUC problem, the total cost minimization to meet hourly loads will automatically determine the hours and levels of EH power injection and withdrawal.
The net output power of EH j (P jt ) is constrained by (9)–(11), which represent the linear relationship between the power that charges the EH storage in P2H mode (\(P_{jt}^{\text{P2H}}\)) and the power that discharges it in G2P mode (\(P_{jt}^{\text{G2P}}\)).
where negative value of P jt corresponds to the P2H mode; \(\eta_{j}^{\text{G2P}}\)(\(\eta_{j}^{\text{P2H}}\)) is conversion efficiency of G2P (P2H), and \(0 < \eta_{j}^{\text{G2P}} ,\eta_{j}^{\text{P2H}} < 1\); \(P_{j,\hbox{min} }^{\text{P2H}}\), \(P_{j,\hbox{min} }^{\text{G2P}}\), \(P_{j,\hbox{max} }^{\text{P2H}}\) and \(P_{j,\hbox{max} }^{\text{G2P}}\)are the lower and upper limits of the corresponding mode.
The hydrogen storage level C jt in EH j is constrained by (12)–(14), where (13) ensures that the storage level of the EH is sufficient to provide service, and (14) is to avoid end-of-horizon effects by setting the final hydrogen storage level to be close to its initial value.
where C j,min and C j,max are the lower and upper storage limits; Δt represents a time interval which is one hour in this paper, and ΔC j is a pre-specified value; and O jt represents the hydrogen product directly supplied to other energy sectors, which is constrained by (15):
Ancillary services at each hour are constrained by (16)–(22). For an EH, its charging P2H capacity could be considered as spinning reserve or regulation up, and so could its discharging capacity in the G2P mode. Then the constraints for regulation up (ru) u jt and regulation down (rd) d jt of EH j are defined by (16) and (17), where \(U_{j}^{\text{P2H}}\), \(D_{j}^{\text{P2H}}\), \(U_{j}^{\text{G2P}}\) and \(D_{j}^{\text{G2P}}\) denote the total ramping up and ramping down capacity in corresponding modes, and \(m_{x}^{Y}\)(\(0 \le m_{x}^{Y} \le 1\)) are apportioning multipliers where x = {ru,rd,rs,ro} and Y = {G2P,P2H}:
Spinning reserve (rs) capacity \(P_{jt}^{\text{rs}}\) is defined in (18):
Operating reserve (ro) \(P_{jt}^{\text{ro}}\) is expressed by (19)–(20), where q j denotes operating reserve capacity in the idling mode, and \(Q_{j}^{\text{G2P}}\) is the quick start capacity of EH j in the G2P mode:
When providing regulation down service, EH generates more than the minimum power in the G2P mode, or electrolyzes less than the maximum power in the P2H mode, as described in (21):
In the G2P mode, the sum of generating power, regulation up, spinning reserve and operation reserve will not exceed its maximum generation capacity, as presented in (22):
The standby electrolyzer in the P2H mode consumes a negligible amount of power which is not taken into consideration.
2.2.3 Constraints for typical SCUC
The typical hourly UC constraints [37] listed below include the system power balance constraints (23), unit minimum on time limits (25), unit minimum off time limits (26), unit ramping up limits (27), unit ramping down limits (28), unit generation limits (29), system spinning reserve requirements (30), system operating reserve requirements (31), regulation up requirements (32), regulation down requirements (33), and DC network constraints (34). Accordingly,
where D t is system load at time t; P wt is the generation dispatch of wind unit w at hour t; and N W is the total number of wind power units, and the dispatched wind power is constraint by (24).
where \(P_{wt}^{\text{f}}\) is forecasted available wind generation.
where \(T_{i}^{\text{on}}\)(\(T_{i}^{\text{off}}\)) is the minimum on (off) time of unit i; \(T_{i}^{\text{U}}\)(\(T_{i}^{\text{D}}\)) is hours of unit i must be initially on (off) due to its minimum up (down) time limits; \(X_{i0}^{\text{on}}\)(\(X_{i0}^{\text{off}}\)) is number of hours unit i has already been on (off) prior to the first hour.
where \(P_{i}^{\text{RU}}\), \(P_{i}^{\text{RD}}\) and P i,min are the ramp-up limit, ramp-down limit and minimum generation of unit i.
where P i,max is the upper limit of real generation of unit i.
where \(P_{it}^{\text{RS}}\) and \(P_{it}^{\text{RO}}\) are the spinning and operating reserve provided by unit i at time t; and correspondingly \(R_{t}^{\text{S}}\) and \(R_{t}^{\text{O}}\) are the system spinning and operating reserve requirements.
where \(P_{it}^{\text{RU}}\) and \(P_{it}^{\text{RD}}\) are the regulation up and down service provided by unit i; and \(R_{t}^{\text{RU}}\) and \(R_{t}^{\text{RD}}\) are the system regulation up and down requirements.
where P L is the vector of maximum power flow limits; S F is the shift factor matrix; K p is the bus-unit incidence matrix; K w is the bus-wind incidence matrix; K E is the bus-EH incidence matrix; K D is bus-load incidence matrix; P p, P w and P E are generation vectors of thermal units, wind farms and EHs, respectively; and P D is the demand vector.
2.2.4 Constraints for SCUC with wind uncertainty
In the deterministic formulation above, the electricity generated from wind turbines is known through short-term forecasting, and there is no consideration of wind power uncertainty. To take into account the variability of wind generation, the base case constraints (with forecasted wind power) (23), (24), (29)–(34) are re-used as scenario constraints (35)–(42), where the base case variables are replaced by corresponding scenario variables [33]. Here, the wind power is assumed to follow a normal distribution N(μ w , σ w ) with expected value μ w equal to the forecasted wind power, and standard deviation representing volatility σ w is a percentage of μ w . Then the Monte Carlo method generates multiple scenarios according to this distribution. In each scenario, an hourly random wind power generation profile is considered.
where the superscript s is an index spanning wind power generation scenarios.
The ability of unit i and EH j to compensate the wind energy variability in scenario s is constrained by (43).
where Δ i and Δ j represent the feasible re-dispatch limit to accommodate the variable wind power, such as 10/60 (30/60) of hourly ramping capacity of thermal units (electrolyzers).
3 Solution methodology
To alleviate the complexity in the proposed SCUC problem, a nested Benders decomposition [33] is used to unbundle the problem into a master UC problem and multiple network constraint subproblems. To take into account variable wind power generation, the Monte Carlo simulation method generates a large number of scenarios which is then reduced by a fast forward algorithm [38]. Figure 3 shows the flowchart of the proposed algorithm, and more detailed discussions of the SCUC problem with the Benders decomposition are presented in [32, 39].
In Part I of Fig. 3, with the forecasted wind power, the master problem provides the UC and dispatching solution to minimize the operating cost. Using the UC solution, the network security check subproblems will confirm the power flow. If any power flow constraint is violated, Cut 1 will eliminate the overloaded lines by enforcing limits on the output of relevant generation and EH units, which are added to the master problem to recalculate the new commitment.
In Part II, the wind power volatility subproblems will check whether the currently available SCUC solution is capable of accommodating the wind energy variability. If any violation occurs, corrective actions will be considered by re-dispatching the current committed units. If this fails, Cut 2 will calculate a preventive action and add it to the master problem to get a new UC solution. Corrective and preventive actions for managing variable wind power generation are detailed in [33].
The Benders decomposition procedure and convergence check methods are detailed in [32, 40]. The MILP method [31, 34] is applied using the CPLEX software. The master unit commitment problem is solved iteratively using Cut 1 and Cut 2 to solve subproblems. When no network violation occurs and all the wind variability scenarios are accommodated, a final robust SCUC solution is obtained.
4 Simulation and results
Two case studies consisting of a 6-bus and modified IEEE 118-bus system are used to illustrate the performance of the proposed model.
4.1 Case study of a 6-bus system
The 6-bus system shown in Fig. 4 is studied over the 24-hour of operation. It includes one base unit G1, two peaking units G2 and G3, one wind unit and one EH unit. The EH and wind units are located at Bus 4.
Parameters of units, transmission lines, and the EH are listed in Tables 1, 2, 3, 4. Here, the EH parameters are simplified [16, 17] with 200 MWh maximum hydrogen storage capacity and 40 MWh minimum reserve capacity, and its initial storage level is 80 MWh. When the request for storage exceeds its capacity, the produced hydrogen will be supplied to other sectors with the maximum power of 40 MW. The conversion efficiency of P2H is about 75%–82% and the round-trip efficiency of the power-to-hydrogen-to-power process is around 40% [41]. It is expected that the efficiency will improve continuously [42]. Conservatively, we define the round-trip efficiency as 32%, being 80% for P2H and 40% for G2P. The hourly load over the 24-hour horizon is listed in Table 5, as well as the forecasted wind power (P w, with 140 MW installed capacity). It is assumed that the system operating reserve, spinning reserve and regulation are 10, 5 and 2% of the load, respectively.
The following four cases are discussed.
-
Case 1: Base case is considered with the forecasted wind power and without the proposed EH.
-
Case 2: An EH is installed at Bus 4, which is close to the wind generation unit, as shown in Fig. 4.
-
Case 3: The EH in Case 2 is relocated from Bus 4 to Bus 3 to be close to the load center.
-
Case 4: The forecasted wind power and 10 simulated wind power scenarios are considered simultaneously, considering various wind power penetration levels with and without the EH.
4.1.1 Hourly UC and dispatch results
The hourly commitment and dispatch results in Cases 1 and 2 are given in Fig. 5. The total operational costs in Cases 1 and 2 are $76852 and $73871, respectively. While, in Case 3, the cost is $74131, which is slightly higher than that in Case 2. In Case 1, G2 and G3 are committed for 4 and 12 hours, respectively, and G1 is always committed. Compared to Case 1, the operational cost in Case 2 is reduced because G2 is committed less, even though there is only a 1-hour commitment reduction of G3 and an additional 3-hour commitment of G2P.
More specifically, the dispatch results in Cases 1 and 2 at hours 18–21 are listed in Table 6. In Case 1, G2 is committed to compensate the sharp decline in the wind power generation during hours 19–21. Besides, since G1 cannot meet the reserve requirement alone (i.e., 12.0 MW spinning reserve requirement, 5% of the total load), G3 is committed at hour 18. While, in Case 2, the loaded power of P2H serves as reserve capacity at hours 18 and 19, and the unloaded capacity of G2P supplies the additional ramping requirement at hours 20 and 21. Accordingly, the total operational cost at hour 19 decreases from $3901 in Case 1 to $3349 in Case 2.
4.1.2 P2H and G2P results in EH
The hydrogen produced and consumed in the EH in Case 2 is given in Fig. 6. As shown by the blue dashed line, P2H mode works at hours 1–5, 7, 18, 19, and G2P mode works at hours 20–22. Accordingly, the hydrogen energy in the EH increases from an initial 80 MWh to finish at 119.34 MWh, with 120 MWh generated from P2H and 80.66 MWh consumed in G2P. Besides, 1.63 MWh of hydrogen products will be provided to other sectors.
As we mentioned in Sect. 1, supplying hydrogen products to other sectors will enhance the economic outlook of EH and release the available storage capacity inside the EH. To illustrate this merit, the maximum storage capacity is set as 160 MWh, then the stored hydrogen in the EH is shown as the red dashed line in Fig. 6. In this case, hydrogen storage reaches its maximum capacity limit at hour 4, and the excess hydrogen production will no longer serve other sectors, so P2H will be curtailed to meet the maximum capacity constraint.
The surplus hydrogen could also be stored in long-term storage devices [24] to mitigate the impacts of gas shortages and congestion. This will further facilitate decoupling the power system from the gas grid: as the largest consumer of the natural gas system, gas generators usually rely on the interruptible gas transportation which are the first to be curtailed during congestion [43].
4.1.3 Wind power curtailment
The proposed EH enhances dispatchability of wind generation, as shown in Fig. 7. ΔC represents the wind curtailment difference between Cases 1 and 2. Compared to Case 1, the total curtailment reduces dramatically in Cases 2 and 3. The expected daily wind energy curtailments in Cases 1–3 are 194, 24 and 49 MWh, respectively.
However, at hour 19, the wind curtailment in Case 3 is larger than that in Case 1, while there is no curtailment in Case 2, as listed in Table 7. It seems likely that when the EH is relocated from Bus 4 to Bus 3, the transmission congestion caused by the re-commitment and re-dispatch of G1 and G2 in Case 3 will limit the applicability of the EH, as shown in Fig. 8. Hence, if we relax the branch flow constraints, the wind curtailment will not be necessary in Case 2.
Case 2 still has a better economic performance than Case 1, even though the increased net wind curtailment at hour 19 alone requires particular attention. It can be concluded that separating EH and wind generation locations can impact their coordination and final scheduling.
4.1.4 Unit commitment with volatile wind generation
The simulated wind power scenarios are considered to check whether the currently available SCUC solution is capable of accommodating the variability of wind power, as shown in Fig. 3. They follow a normal distribution with a standard deviation of 10% about the expected values. Using the Monte Carlo method, 3000 wind power scenarios are generated and then reduced to 10 scenarios [38], which are given in Table 8.
The scenario reduction technique eliminates scenarios with low probability and aggregates similar scenarios [32, 38] to get a tradeoff between computational difficulty and approximation accuracy. To illustrate the effectiveness of this reduction, the relative error of total cost (from 80 scenarios to 2 scenarios) is given in Fig. 9. It can be seen that the relative distance between objective functions with 80 scenarios and 10 scenarios resulting from the scenario reduction is within 2.5%.
To consider other wind penetration levels in EH, we define a low wind penetration (LWP) scenario in which the installed capacity of wind generation is reduced from 140 MW in the original high wind penetration (HWP) scenario to 70 MW. For comparison, two base cases (base case 1 for LWP and base case 2 for HWP) without EH are also introduced.
The final UC results are given in Table 9. Since the EH acts only at hours 2 and 3 in the LWP scenario, there is no distinct difference between base case 1 (BS1) and LWP. Accordingly, their total operating costs are $98968 and $100018 respectively. In the HWP scenario, the P2H unit is committed more frequently to absorb the surplus wind power. This means that the EH, as an interruptible load, could provide higher reserve capacity for the system. Thus, the EH has a better performance in this HWP scenario. As a consequence, G2 and G3 are committed less in HWP, and the total operating costs are substantially different between base case 2 (BS2) at $83782 and HWP at $79985.
4.2 A modified IEEE 118-bus test system
A modified IEEE 118-bus test system is used to test the proposed model. The system has 54 units, 186 branches, and 91 demand sites, and its detailed data are given in motor.ece.iit.edu/data/SCUC_P2H_118.
Firstly, the SCUC solution with a daily operational cost of $1674974 is obtained without considering wind and EHs. Then wind farms and EHs, which have the same output profile and characteristics as those in the 6-bus system, are integrated into the 118-bus system to study the performance of the proposed EH with different wind penetration. To consider the influence of wind volatility, σ w is increased to 22%. The Monte Carlo simulation and scenario reduction techniques are used to produce 10 scenarios from 100 generated scenarios, which represent higher wind volatility. The total costs resulting from SCUC with different wind penetrations, with and without EHs, are given in Table 10.
In Table 10, when the wind penetration level is below 20.28% (or 10.14% for σ w = 22%), the wind power volatility is mitigated by corrective actions of the committed thermal units in the 118-bus system. Thus the EHs have no actions. If the wind power penetration increases sequentially, the difference between cases without and with EHs becomes more evident. This observation is consistent with those of the 6-bus system. Moreover, by comparing cases for σ w = 10% and σ w = 22%, it can be observed that the EH holds greater promise in more volatile wind scenarios.
The MILP was solved using CPLEX 12.1 under the MATLAB on a personal PC with Intel i7 2.8 GHz processor (8 GB RAM). Computation for the 118-bus system without wind units and EHs requires 4 minutes. With increasing the complexity caused by a higher integration of wind units and EHs, the computation time gradually increases from 4 minutes to 87 minutes for 19 wind units and 3 EHs. Using decomposition techniques enables the application of parallel computing which can speed up the proposed solution and reduce the total CPU time.
5 Conclusion and future work
A day-ahead SCUC problem is modeled which integrates wind generation and EHs composed of P2H and G2P units with gas storage. The SCUC problem is solved by MILP method with the Benders decomposition technology. Accordingly, the following conclusions are provided.
-
1)
EHs offer a potential to reduce wind curtailments and manage a variable power profile, especially with a high level of wind energy penetration.
-
2)
Supplying hydrogen products directly to other industry sectors enhances the EH’s capability to reduce wind curtailments as it releases the additional available storage capacity at the EH.
-
3)
Separating the EH and wind generation locations may impact their coordination and, in some cases, even lead to increased wind curtailments.
Future work will include the modeling of load uncertainty as well as transmission line contingency. There are successful works presented on co-optimization [43] of the power system and natural gas grid [44, 45], especially regarding the SCUC problem [46] with wind variability [47]. The proposed EH model will be extended to consider such works.
References
Wang X, Jiang CW, Li BS (2016) Active robust optimization for wind integrated power system economic dispatch considering hourly demand response. Renew Energy 97:798–808
Valipour M, Sefidkouhi MA, Raeini−Sarjaz M M (2017) Selecting the best model to estimate potential evapotranspiration with respect to climate change and magnitudes of extreme events. Agric Water Manag 180:50–60
Wang X, Gong Y, Jiang CW (2015) Regional carbon emission management based on probabilistic power flow with correlated stochastic variables. IEEE Trans Power Syst 30(2):1094–1103
Kamalinia S, Shahidehpour M (2010) Generation expansion planning in wind-thermal power systems. IET Gener Transm Distrib 4(8):940–951
Chowdhury M, Rao M, Zhao Y et al (2016) Benefits of storage control for wind power producers in power markets. IEEE Trans Sustain Energy 7(4):1492–1505
Fang X, Li F, Wei Y et al (2016) Strategic scheduling of energy storage for load serving entities in locational marginal pricing market. IET Gener Transm Distrib 10(5):1258–1267
Shahidehpour M, Shao CC, Wang XF et al (2017) An MILP-based optimal power flow in multi-carrier energy systems. IEEE Trans Sustain Energy 8(1):239–248
Geidl M, Koeppel G, Favre-Perrod P et al (2007) Energy hubs for the future. IEEE Power Energy Mag 5(1):24–30
Shao CC, Wang XF, Wang XL et al (2014) Cooperative dispatch of wind generation and electric vechicles with battery storage capacity constraints in SCUC. IEEE Trans Smart Grid 5(5):2219–2226
Amini MH, Kargarian A, Karabasoglu O (2016) ARIMA-based decoupled time series forecasting of electric vehicle charging demand for stochastic power system operation. Electr Power Syst Res 140:378–390
Shi XY, Ma ZJ (2016) An efficient game for vehicle-to-grid coordination problems in smart grids. Int J Syst Sci 16:2686–2701
Wang SY, Yu JL (2012) Optimal sizing of the CAES system in a power system with high wind power penetration. Int J Electr Power Energy Syst 37(1):117–125
Khodayar ME, Shahidehpour M, Wu L (2013) Enhancing the dispatchability of variable wind generation by coordination with pumped-storage hydro units in stochastic power systems. IEEE Trans Power Syst 28(3):2808–2818
Kamalinia S, Wu L, Shahidehpour M (2014) Stochastic midterm coordination of hydro and natural gas flexibilities for wind energy integration. IEEE Trans Sustain Energy 5(4):1070–1079
Schiebahn S, Grube T, Robinius M et al (2015) Power to gas: technological overview, systems analysis and economic assessment for a case study in Germany. Int J Hydrogen Energy 40(12):4285–4294
Bensmann B, Hanke-Rauschenbach R, Müller-Syring G et al (2016) Optimal configuration and pressure levels of electrolyzer plants in context of power-to-gas applications. Appl Energy 167:107–124
Walker SB, Mukherjee U, Fowler M et al (2016) Bench-marking and selection of power-to-gas utilizing electrolytic hydrogen as an energy storage alternative. Int J Hydrogen Energy 41(19):7717–7731
Gahleitner G (2013) Hydrogen from renewable electricity: an international review of power-to-gas pilot plants for stationary applications. Int J Hydrogen Energy 38(5):2039–2061
Estermann T, Newborough M, Sterner M (2016) Power-to-gas systems for absorbing excess solar power in electricity distribution networks. Int J Hydrogen Energy 41(32):13950–13959
Mendaza IDC, Bhattarai BP, Kouzelis K et al (2015) Optimal sizing and placement of power-to-gas systems in future active distribution networks. In: Proceedings of the 2015 IEEE innovative smart grid technologies-Asia, Bangkok, Thailand, 3–6 Nov 2015, 1–6
Clegg S, Mancarella P (2015) Integrated modeling and assessment of the operational impact of power-to-gas (P2G) on electrical and gas transmission networks. IEEE Trans Sustain Energy 6(4):1234–1244
Zoss T, Dace E, Blumberga D (2016) Modeling a power-to-renewable methane system for an assessment of power grid balancing options in the Baltic States′ region. Appl Energy 170:278–285
Baumann C, Schuster R, Moser A (2013) Economic potential of power-to-gas energy storages. In: Proceedings of the 2013 international conference on the European energy market, Stockholm, Sweden, 27–31 May 2013, 6 pp
Clegg S, Mancarella P (2016) Storing renewables in the gas network: modelling of power-to-gas seasonal storage flexibility in low-carbon power systems. IET Gener Transm Distrib 10(3):566–575
Götz M, Lefebvre J, Mörs F et al (2016) Renewable power-to-gas: a technological and economic review. Renew Energy 85:1371–1390
Mukherjee U, Walker S, Maroufmashat A et al (2016) Power-to-gas to meet transportation demand while providing ancillary services to the electrical grid. In: Proceedings of the 2016 IEEE smart energy grid engineering, Oshawa, ON, Canada, 21–24 Aug 2016, 221–225
Guandalini G, Campanari SRM (2014) Comparison of gas turbines and power-to-gas plants for improved wind park energy dispatchability. In: Proceedings of the 2014 ASME turbo expo: turbine technical conference and exposition, Düsseldorf, Germany, 16–20 June 2014, 11 pp
Guandalini G, Campanari S, Romano MC (2015) Power-to-gas plants and gas turbines for improved wind energy dispatchability: energy and economic assessment. Appl Energy 147:117–130
Zhang X, Shahidehpour M, Alabdulwahab A et al (2015) optimal expansion planning of energy hub with multiple energy infrastructures. IEEE Trans Smart Grid 6(5):2302–2311
Kienzle F, Ahčin P, Andersson G (2011) Valuing investments in multi-energy conversion, storage, and demand-side management systems under uncertainty. IEEE Trans Sustain Energy 2(2):194–202
Haddadian G, Khalili N, Khodayar M et al (2015) Security-constrained power generation scheduling with thermal generating units, variable energy resources, and electric vehicle storage for V2G deployment. Int J Electr Power Energy Syst 73:498–507
Rebennack S (2016) Combining sampling-based and scenario -based nested Benders decomposition methods: application to stochastic dual dynamic programming. Math Program 156(1):343–389
Wang JH, Shahidehpour M, Li ZY (2008) Security-constrained unit commitment with volatile wind power generation. IEEE Trans Power Syst 23(3):1319–1327
Carrión M, Arroyo JM (2006) A computationally efficient mixed-integer linear formulation for the thermal unit commitment problem. IEEE Trans Power Syst 21(3):1371–1378
Gobbato P, Masi M, Toffolo A et al (2011) Numerical simulation of a hydrogen fueled gas turbine combustor. Int J Hydrogen Energy 36(13):7993–8002
Qadrdan M, Abeysekera M, Chaudry M et al (2015) Role of power-to-gas in an integrated gas and electricity system in Great Britain. Int J Hydrogen Energy 40(17):5763–5775
Fu Y, Shahidehpour M, Li ZY (2005) Security-constrained unit commitment with AC constraints. IEEE Trans Power Syst 20(2):1001–1013
Römisch W (2009) Scenario reduction techniques in stochastic programming. In: Proceeding of the 2009 Stochastic algorithms: foundations and applications: international symposium, SAGA, Sapporo, Japan, 26–28 October 2009, 1–14
Liu C, Shahidehpour M, Wu L (2010) Extended benders decomposition for two-stage SCUC. IEEE Trans Power Syst 25(2):1192–1194
Fang X, Li F, Wei Y et al (2015) Reactive power planning under high penetration of wind energy using Benders decomposition. IET Gener Transm Distrib 9(14):1835–1844
Budny C, Madlener R, Hilgers C (2015) Economic feasibility of pipe storage and underground reservoir storage options for power-to-gas load balancing. Energy Convers Manag 102:258–266
Luo X, Wang JH, Dooner M et al (2015) Overview of current development in electrical energy storage technologies and the application potential in power system operation. Appl Energy 137(6):511–536
Zhang XP, Shahidehpour M, Alabdulwahab AS et al (2015) Security-constrained co-optimization transportation infrastructures. IEEE Trans Power Syst 30(6):2984–2993
Liu C, Shahidehpour M, Fu Y et al (2009) Security-constrained unit commitment with natural gas transmission constraints. IEEE Trans Power Syst 24(3):1523–1536
Liu C, Lee C, Shahidehpour M (2015) Look ahead robust scheduling of wind-thermal system with considering natural gas congestion. IEEE Trans Power Syst 30(1):544–545
Shahidehpour M, Yong Fu, Wiedman T (2005) Impact of natural gas infrastructure on electric power systems. Proc IEEE 93(5):1042–1056
Alabdulwahab AS, Abusorrah A, Zhang XP et al (2015) Coordination of interdependent natural gas and electricity infrastructures for firming the variability of wind energy in stochastic day-ahead scheduling. IEEE Trans Sustain Energy 6(2):606–615
Acknowledgments
This work is supported by National Natural Science Foundation of China (No. 51377035) and NSFC-RCUK_EPSRC (No. 51361130153). The authors also thank the anonymous reviewers and the editor for their valuable comments.
Author information
Authors and Affiliations
Corresponding author
Additional information
CrossCheck date: 3 March 2017
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
BAN, M., YU, J., SHAHIDEHPOUR, M. et al. Integration of power-to-hydrogen in day-ahead security-constrained unit commitment with high wind penetration. J. Mod. Power Syst. Clean Energy 5, 337–349 (2017). https://doi.org/10.1007/s40565-017-0277-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40565-017-0277-0