Abstract
The oscillations in a power system can be categorized into free oscillations and forced oscillations. Many algorithms have been developed to estimate the modes of free oscillations in a power system. Recently, forced oscillations have caught many researchers’ attentions. Techniques are proposed to detect forced oscillations and locate their sources. In addition, forced oscillations may have a negative impact on the estimation of mode and mode-shape if they are not properly accounted for. To improve the power system reliability and dynamic properties, it is important to first distinguish forced oscillations from free oscillations and then locate the sources of forced oscillations in a timely manner. The negative impact of forced oscillation can be mitigated when they are detected and located. This paper provides an overview of the analysis technique of forced oscillations in power systems. In addition, some future opportunities are discussed in forced oscillation studies.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
One of the major threats to the security and stability of power systems is low-frequency oscillations [1, 2]. If oscillations are negatively damped, the magnitude of oscillations will grow and consequently cause system breakup and power outages. These are known as the small signal stability problems. Analysis of low-frequency oscillations is critical to the reliable operation of power systems. Based on the cause of oscillations, low-frequency electromechanical oscillations can be categorized into two main categories: free oscillations and forced oscillations. Free oscillations result from the natural interaction among dynamic devices. In contrast, forced oscillations refer to system responses to an external periodic perturbation.
Methods to mitigate the free oscillations are totally different than those for forced oscillations. Power system stabilizer (PSS) is a simple and economical method to suppress the oscillations by increasing the damping ratio. Control strategies can be utilized to rectify lightly-damped or undamped free oscillations. In contrast, removing the source of oscillations can be considered a remedy for forced oscillations.
It is very important to get the accurate information about oscillations because it can help operate a power system reliably at its full capacity. To study free oscillations, modal properties of power systems provide principal information for control strategies. Basically, there are two approaches for estimating power system modes: the component-based approaches and the measurement-based approaches. Stable modes of the power system can guarantee that free oscillations will dampen. On the other hand, undamped modes can be hazardous for the power system. In past decades, remarkable efforts have been devoted to estimate the modal properties of a power system using component-based approaches and measurement-based approaches [3]. Numerous measurement-based modal analysis algorithms have been proposed. Valuable overviews of existing algorithms are presented in [4, 5].
With the application of phasor measurement unit (PMU) data, it is possible to record and monitor systems’ dynamic behaviors. PMU data have been widely used to study the forced and free oscillations because they have a typical sampling rate of 30-60 samples/second and are well synchronized with global positioning system (GPS) clock.
One of the primary identifications of forced oscillations goes back to 1966 [6]. Forced oscillations can be caused by an external periodic disturbance or a mistuned generator controller. Forced oscillations are reported as a sinusoidal signal originated at generator sites [7]. The resonance between forced oscillation and electromechanical mode can cause system break-down [8]. Sustained oscillation is imposed in power systems when forced oscillations exist around a well-damped mode. Forced oscillations have been observed several times in the western North American Power System (wNAPS) with a frequency range of 0.2 Hz to 2 Hz which, in some cases, caused moderately hazardous situations [9]. To analyze forced oscillations, one should initially study the source of forced oscillations in isolated and large systems. Identifying the possible sources of forced oscillations can help to attain a more reliable power system. To improve the power systems reliability and stability, detecting and locating the forced oscillations is important. In addition, amplitude, frequency and phase of forced oscillations are of interest.
In this paper, we present an organized treatment for forced oscillations. Mainly, our objective is three-fold and they are listed below.
-
1)
To provide a comprehensive overview of existing methods to detect and locate forced oscillations and study the impacts of forced oscillations in power systems.
-
2)
To identify the key open problems for detecting the forced oscillations.
-
3)
To introduce future opportunities that can be possible paths to study the forced oscillations.
Therefore, a clear picture of strength and challenges of the existing methods to study forced oscillations is provided.
The paper is organized as follows. In Sect. 2, sources of forced oscillations are discussed. Section 3 provides an overview of existing methods to detect the forced oscillations. Oscillation classification methods are discussed in Sect. 4. Section 5 provides an overview of existing methods to locate forced oscillations. In Sect. 6, the impacts of forced oscillations on estimating electromechanical modes are reviewed. Future opportunities for studying forced oscillations are discussed in Sect. 7. Conclusions are drawn in Sect. 8.
2 Source of forced oscillations
It is important to locate the sources of forced oscillations because once their sources are identified, the forced oscillations can be mitigated by removing the sources. However, it is very challenging to locate the real disturbance source due to the complexity of a power system.
Forced oscillations have been observed and reported in power grids. One of the earliest studies on forced oscillations dates back to 1966 when Ness studied the responses of power systems to cyclic load variations [6]. To study the situation where frequency of forced oscillations is close to natural frequency of generator rotor oscillations, Vournas et al. introduced cyclic load, low-speed diesel generators and wind turbines, which is driving the synchronous generator, as possible sources of forced oscillations [8]. The Pinneilo et al. cited the nuclear accelerator as source of forced oscillations [10]. Power systems behaviors for steady state analysis, dynamic simulation and controller design have been considered in [11], where steel plants, nuclear accelerators, cement mills and aluminum processing plants are cited as sources of forced oscillations. Putting limit on generator field voltage in a single-machine infinite-bus system can induce stable limit cycle that consequently is a cause of forced oscillations via Hopf bifurcation [12]. To analyze the characteristics of regulating systems, the electro-hydraulic regulating system of a steam turbine is mentioned as a source of forced oscillations in [13]. Poorly designed PSS can induce amplification of forced oscillations [14]. Authors of [14] noted that traditional PSS control loops introduce additional poles and zeros which can resonate with cyclic inputs. To avoid possible resonance, authors in [14] provided adjusted PSS design. Rostamkolai et al. proposed that the impact of cyclic load, which is caused by a synchrotron in the power systems, is significant, especially in resonance situations with electromechanical oscillations [15]. In [16], incomplete islanding has been cited as a possible source of forced oscillations in the power system. To simulate the forced oscillations, mechanical power of a generator is modulated with a sinusoidal signal in [17]. These studies showed that forced oscillations may come from different sources.
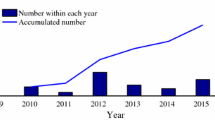
Reported forced oscillations in these studies are sorted by their reported years and summarized in Table 1. It can be observed from Table 1 that:
-
1)
Before the year 2000, there are 7 papers studying causes of forced oscillations, i.e., No. 1-7: 6 of them used simulation data and they are focused on the load side, i.e., No. 1-5, 7.
-
2)
After the year 2000, 20 events have been reported, i.e., No. 8-27: ➀ 18 oscillations are recorded using PMU data, i.e., No. 1, 2, 12-27; ➁ 14 oscillation studies are related to generators, i.e., No. 8, 9, 12-21, 23, 27; ➂ 4 oscillation events are associated with wind power plants, i.e., No. 12, 17, 19, 21; ➃ 4 oscillation studies are associated with hydro power plants, i.e., No. 11, 15, 20, 22.
-
3)
Of all the events, the control actions of 5 events involve the reduction of asset usage, i.e., No. 6, 9, 10, 12, 21.
-
4)
13 oscillations have the records on their time durations:
-
a.
4 oscillations last for more than 1 hour, i.e., No. 15, 17, 21, 27.
-
b.
5 oscillations last for more than 10 minutes but less than 1 hour, i.e., No. 6, 10, 12, 13, 24.
-
c.
4 oscillations last for less than 10 minutes, i.e., No. 9, 14, 18, 23.
-
a.
-
5)
9 oscillations have the records on their oscillation amplitudes in MW or MVA:
-
a.
The smallest peak-peak oscillation magnitude is 10 MVA, i.e., No 15.
-
b.
The largest peak-peak oscillation magnitude is 280 MW, i.e., No. 6.
-
c.
5 oscillations have their magnitude larger than 100 MW, i.e., No. 6, 9, 10, 13, 16.
-
d.
4 oscillations have their magnitude less than 40 MW, i.e., No. 7, 14, 15, 22.
-
a.
-
6)
19 oscillations have the records on their oscillation frequency in Hz. According to [46], they are categorized as follows:
-
a.
2 oscillations between (0.01-0.15 Hz), i.e., No. 16, 22.
-
b.
7 oscillations between (0.15-1.0 Hz), i.e., No. 7, 9, 11, 14, 15, 16, 23.
-
c.
7 oscillations between, i.e., (1.0–5.0 Hz), i.e., No. 6, 10, 18, 20, 21, 25, 26.
-
d.
4 oscillations between (5.0-14.0 Hz), i.e., No. 12, 17, 19, 24.
-
a.
-
7)
19 oscillations have the records on their location sources:
-
a.
9 oscillations are recorded in Eastern interconnection, i.e., No. 6, 12-14, 16, 18, 19, 22, 24.
-
b.
8 oscillations are recorded in Western interconnection data, i.e., No. 9, 10, 15, 17, 23, 25-27.
-
a.
It can be observed that both cyclic load and generator control equipment (GCE) were reported as the sources of forced oscillations. In addition, in the recent years, GCEs such as PSS and automatic voltage regulators (AVR) are reported more often as the sources of forced oscillations. In other words, the sources of the forced oscillations mainly are located on the generator sides. This prior information suggests that to detect and locate forced oscillations, one may want to place more attentions on the generation sides.
3 Oscillation detection methods
To provide a better understanding of forced oscillations, Fig. 1 illustrates a sample time plot of forced oscillations in simulated PMU data.
Assume that the forced oscillations are modeled by a sinusoidal signals of unknown amplitude, frequency, phase and arrival time embedded in colored noise.
where A is the sinusoidal signal which represents forced oscillations; z t is the additive noise [50, 51]; N is the total number of samples.
Therefore, the challenge is to detect the sinusoidal covered with ambient noise.
In [28], an algorithm to detect the sinusoidal signal under Gaussian white noise (GWN) is presented. Forced oscillations can be detected using statistical properties of a periodogram. To detect sinusoid covered with noise, simple estimators of power spectral density (PSD) can be used. PSD describes how the strength of a signal is distributed over frequency. Using the Welch method, Figs. 2, 3 and 4 illustrate PSDs of x t for the 30 seconds, 1 hour and 24 hours of data consequently when the window length is 128, Hamming windows, and overlapping is 50%. As can be seen in Fig. 2, there are four peaks. The peaks at 0.4 HZ, 3 Hz and 9 Hz represent the modes from the ambient noise. The peak at 5 Hz shows forced oscillations. This peak can be smaller for forced oscillations with lower SNR. However, Fig. 3 illustrates just two peaks, one at 0.4 Hz (i.e., mode from the ambient noise) and another at 5 Hz with high amplitude (i.e., the forced oscillations). Figure 4 clearly shows only one peak at 5 Hz with a very high amplitude. This observation indicates that there is a direct relationship between the magnitude of forced oscillation and time, which can be used to distinguish the different types of oscillations. Using PSD to detect the forced oscillation, there is a trade-off between time and the detection accuracy. Because it is important to detect the forced oscillations in a timely manner, using PSD to detect the oscillations is not the best practice. Therefore, there is a need for a method that can distinguish different types of oscillations in a timely manner.
Because ambient data in power systems are known to be colored, it is not practical to directly apply the proposed method in [28]. Thus, Follum et al. modified the method to deal with the colored ambient noise environment [7]. They proposed methods for estimating the frequency, amplitude, start time and end time of forced oscillations. Yet, the problem of detecting oscillation in a timely manner, as mentioned for PSD, remains unsolved. It is expected to observe a close correlation between the location and the source of forced oscillation (in a large system) with the detection accuracy. Proposed method in [7] is only applied to the simulated data rather than simulation data from power system or field measurement data. As a result, there is a question on real-word application of the proposed method. To decrease the time-delay for detecting forced oscillations, the coherence spectrum, also known as magnitude-squared coherence, is employed to detect forced oscillations in [29]. It reflects the linear correlation of time-series signals at a specific frequency. Although it decreased the time-delay for detecting forced oscillations even for small signal-to-noise ratio (SNR), it has two drawbacks: ➀ it requires two channel of data; ➁ it may introduce some peaks because of linear correlation between two channels. The method is further developed in [17] as a self-coherence method. Fundamentally, the self-coherence spectrum is the coherence spectrum using one channel data and its time-delayed signal. The self-coherence method is applied to the data set with a time delay of ∆t is 6.0 s. For the 60 minutes of date, Fig. 5 shows the self-coherence spectrum in a heat map where oscillations frequency is 8 Hz.
During the ring-down oscillations, using self-coherence method, existence of time delay eliminates the effect of the linear correlation, which causes the peaks in the coherence method. Yet, the problem of proper channel selection in [17] remains unsolved. In addition, this method does not specifically detect forced oscillations, rather it provides a magnitude of coherence between 0 to 1. Furthermore, a bootstrap method was applied to set up appropriate threshold on self-coherence for detecting forced oscillations in [30]. Based on the bootstrap method, a threshold can be determined to detect the sustained oscillations with pre-selected probability of false alarm. Figure 6 shows the threshold as a red line as with a false alarm rate set at α = 1%. As it can be seen the only point that exceeds the threshold is at frequency of 8 Hz. However, there is question of how quickly this method can detect oscillations. To extend the coherence method, Ref [31] applied coherence method to multiple-channel data. It shows that using multiple-channel method can increase detection rates. To inspect the performance of the coherence method, different algorithms such as the Welch algorithm, Capon algorithm and autoregressive moving average (ARMA) algorithm are used to estimate coherence spectra. Moreover, the performances of three algorithms are compared. However, there is a question on applicability of the method when both forced and free oscillations exist in the system. In [23], covariance-driven stochastic subspace identification (SSI-COV) [32] was applied to detect the forced oscillations. This method can simultaneously detect forced oscillations while estimating system modes. The authors studied the effects of forced oscillations on the local modes and inter-area modes. However, proposed method failed to distinguish forced oscillations from free oscillations.
4 Oscillation classification methods
Oscillations classification is very important to the reliable operation of power systems because control strategy for suppressing different types of oscillations can be significantly different. Using support vector machine (SVM), [33] proposed a method that can classify two different types of oscillations based on feature extraction. Basically, increasing amplitude of free oscillations is used to distinguish it from forced oscillations. In this case, algorithm accuracy has direct relationship with envelope size. Thus, there is a question of whether this algorithm can work in real-time scenarios. Reference [34] proposed unique mathematical models for forced and free oscillations. In addition, they showed that the responses of the system to forced oscillations differs from those of free oscillations. Based on noise response and harmonic nature of oscillations, the authors proposed a method to distinguish forced oscillations from free oscillations. However, there is question of how to separate the pure sinusoid from noise in both cases (free and forced oscillations) and the effects of this separation on algorithm accuracy should be considered. In addition, it is important to evaluate the performance of proposed method when forced oscillations exist at a system’s mode frequency.
To study the fundamental methodologies adopted for oscillation classifications, the two-area model shown in Fig. 7 is utilized to generate the data for both forced and natural oscillations. Note that power system toolbox (PST) [35] is used to simulate the data with a classical generator model. This model has three modes that are presented in Table 2. Active and reactive loads of all the buses are modulated by 5% GWN to simulate the ambient noise. To generate forced oscillations (Fig. 7a), a sinusoidal signal with amplitude of 0.1 is injected into the system by modulating the shaft torque of G1 for 5 minutes. To generate natural oscillations (Fig. 7b), generation values are set up to reach an unstable condition after a three phase fault occurs between the bus 7 and 8.
We conducted a study for four different cases: ➀ natural oscillations exist at a frequency of 0.4 Hz; ➁ forced oscillations exist at a frequency of 2 Hz; ➂ forced oscillations exist at a frequency of 1.14 Hz (close to system’s mode frequency); ➃ forced oscillations exist at a frequency of 0.53 Hz (close to system’s mode frequency). The spectral approach, the proposed method in [34], is applied to these cases and results are shown in Table 3. Here, α S indicates the ratio of PSD between two different channels when oscillations exist where α N indicates the ratio of PSD of two different channels when oscillations does not exist.
As it can be seen in Table 3, α S and α N are very close for case 1 so it can be considered a natural oscillation. In addition, the PSD ratios at 2 Hz are NOT equal which indicates that forced oscillations exist. However, if forced oscillations’ frequencies are close to the mode frequency of the system (i.e. 1.14 and 0.53 Hz) as in case 3 and 4, the PSD ratios are close to each other. In other words, the spectral approach [34] is not effective when forced oscillations exist at system’s mode frequency.
Wang et al. [36] introduced three different mathematical models for weakly damped oscillations, limit cycle and forced oscillation. Using Kurtosis estimation and PSD estimation, they proposed an algorithm which can distinguish these oscillations from each other. Authors of [36] used the standard deviation of PSD as a metric to detect forced oscillations. However, this method just has off-line application. To get the accurate PSD estimation for distinguishing oscillations, as Figs. 2, 3 and 4 illustrated, a reasonable amount of time required. In addition, this method may not be effective for oscillations with small signal-to-noise ratio (SNR).
As it can be seen, forced oscillations play a critical role in system performance and they can cause catastrophic events [1, 2]. Therefore, to increase the reliability of power systems, it is important to detect and distinguish forced oscillations and free oscillations. A robust method which can distinguish forced oscillations from free oscillations even when forced oscillations exist at system’s mode frequency is needed. Extracting the unique features of forced oscillations can be a possible solution. However, the unknown nature of forced oscillation sources has made it hard to model them mathematically.
5 Oscillation source locating methods
In order to suppress forced oscillations and mitigate their impacts, a robust method for locating the sources of forced oscillations is needed. Fundamentally, forced oscillations can be caused by an external perturbation in generator sites.
PMU data reflects the behaviors of the model at 30 to 60 samples/s. They basically are phasor measurements synchronized with GPS clock. PMU data have been widely used in power systems analysis [5, 37]. In [38], the authors proposed a new application of PMU data. PMU data have been utilized to locate the sites of disturbance sources. A hybrid dynamic simulation method is used to locate the forced oscillations. Basically, the idea is to replace part of dynamic states and algebraic variables with measurements, which in this case is PMU data, and run a power system model. Mismatch between simulation data and PMU data indicates the location of forced oscillations. Although the method shows promising results, it is only applicable in post-fault analysis studies. Using dynamic state variables, an energy based method is applied to locate the source of forced oscillations in [39, 40]. Although both methods shows promising results, they require detailed information of the model which makes the applicability and the validity of these methods unclear. In [41], after visually detecting oscillations, Prony analysis is applied to extract the oscillations’ characteristic (i.e. frequency, Magnitude, Phase and Damping ratio) and consequently damping torque of the generator is used to locate the source of forced oscillations. The authors detected the forced oscillations at a frequency of 0.56 Hz which is close to the mode frequency and the source of oscillation is not discussed in the paper. Thus, it is interesting to study the performance of this method for two different scenarios: forced oscillations with very small frequency (i.e. 0.13) imposed on a generator and applicability of method on a large power system. Reference [42] analyzed the forced oscillations at 0.7475 Hz based on extended equal-area criterion (EEAC) theory and then located the forced oscillations in two steps: ➀ identify the disturbance cluster by comparing steady phase relationships; ➁ locate the disturbance source by comparing transient response trajectories phase of observation points in identified disturbance clusters. However, the applicability of the proposed method for forced oscillations with high frequency (i.e. 14 Hz) is questionable. Reference [43] studied the differences between the free and forced oscillations in terms of their energy conversions. Considering the cyclical load disturbance as a cause of forced oscillations, an increase of potential power is proposed that can be used to locate the disturbance source of forced oscillations. As it is listed in Sect. 2, the cyclical load disturbance is one of the possible sources of forced oscillations besides malfunctioning generators, PSS limits on generators, nuclear accelerators and etc. So, it is important to evaluate the performance of the proposed method in [43] for different sources (especially when forced oscillations’ frequencies are considerably small). Reference [44] proposed a new approach based on power dissipation to locate the disturbance source of forced oscillations. As can be seen in Table 1 from the reported event, the forced oscillation frequencies can be expected to be between 0.12 Hz to 14 Hz, and it is not necessarily equal to the natural oscillations’ mode frequencies. Thus, the performance of the proposed method is questionable when forced oscillation frequencies are not equal to the system’s mode frequency. In [23], it was proposed that the location of forced oscillations can be determined using mode shape magnitude when there is not a strong resonant effect. However, in the case of resonance when frequency of forced oscillations is close to that of system modes, mode shape estimation may not be useful to locate the source of forced oscillations.
To provide a better understanding of forced oscillations locating methods, the power spectrum density of the voltage of each bus for case 2 and 4 in Sect. 4 is calculated and plotted in Figs. 8 and 9. It can be observed in Fig. 8 that the PSD of the magnitude response of buses are consistent with their distances to the oscillation source. In other words, the closer we get to the oscillation source, the greater the magnitude of the PSD will be in oscillation frequency. Here, we see buses 1 and 5 have highest magnitude and buses 3 and 4 have lowest magnitudes which indicate that the oscillation is located in generator 1. However, this method can locate the forced oscillations with small frequencies. As can be seen in Fig. 9, the PSD of magnitude response of buses are not consistent with their distance to the oscillation source when forced oscillations has small frequency (i.e. 0.53 Hz). Thus, it is important to find a method that can locate the source of forced oscillation at any frequency even close to system’ mode frequency.
PSDs of x t for 5 minutes of data for all the buses for case 2 in Sect. 4
PSDs of x t for 5 minutes of data for all the buses for case 4 in Sect. 4
While aforementioned methods were able to locate the forced oscillations to some degree, there is a need to develop a method which can distinguish forced oscillations from free oscillations and locate the source of the forced oscillations under different scenarios: ➀ forced oscillations with different frequency ranges (i.e. 0.12 Hz to 14 Hz); ➁ forced oscillation in a large and complex system; ➂ forced oscillations with low SNRs; ➃ forced oscillations imposed by different causes (i.e. Cyclical load, generator malfunctioning, etc).
6 Effects of forced oscillations on mode estimation algorithms
Modes and mode shapes are critical parameters describing free oscillations. Mode describes the system’s oscillation frequency and damping behaviors while mode shape states the relative participation of state variables in particular mode [45]. Electromechanical modes in power systems are analyzed through many parametric methods.
Basically there are two approaches for estimating power system modes: simulation model-based approach [46] and measurement-based approach. Regarding model-based approaches, the challenge is to obtain an accurate dynamic model for real-time power system operating conditions. The task is even more difficult for large-scale power systems. The difference between real system responses and simulation model responses during a real-world event indicates the model’s deficiency, which can cause conservative operation and reduce asset utilization. For instance, an initial effort was made to build a component based model for simulating the Western Electricity Coordinating Council (WECC) [1]. The study shows that the simulated system responses do not match the field measurement data. Simulation results and measurement results matched only after extensive modification and calibration. In contrast, the measurement-based approach requires less effort than the model-based approach. In addition, measurement-based approaches can update the mode estimation based on incoming measurement data. Based on measurement approaches, modes of a system can be identified using ambient data, ring-down data and probing signals. Therefore, measurement-based methods have certain advantages over the model-based eigenvalue analysis in monitoring real-time power oscillations. An overview of mode estimation algorithms is given in [4, 5].
To estimate the modal properties of a system, mode-meter algorithms are constantly processing PMU data and estimating frequency, damping ratio and shape of a mode from ambient data. Forced oscillations impose a challenge on mode estimation algorithms [5, 47]. To estimate the mode accurately, it is important to study the impact of forced oscillations on mode estimation. Studying both simulation data and real-time PMU data, authors in [48], pointed out that damping estimate can be comprised when forced oscillations exist. Vanfretti et al. showed that the impact of forced oscillation on damping estimate depends on its location with respect to an inter-area mode [49]. It has been shown that estimated damping ratio decreases when a forced oscillation is superimposed on the inter-area mode. However, estimated damping ratios increase when forced oscillations are close to the inter-area mode. Myers et al. showed that existence of forced oscillations can have a slight impact on mode-shape estimation only when forced oscillation frequency is close to system mode frequency [9]. Forced oscillations with frequencies far away from system mode frequencies have no noticeable impact on mode-shape estimation. In addition, Sidorov discusses the online detection of inter-area oscillations in the power systems in [52].
Properties of the electromechanical modes describe system oscillation frequency and damping behavior. Therefore, identifying forced oscillations is important because it helps mode estimation algorithms to provide more accurate information about power-system stability.
7 Future opportunities for studying forced oscillations
Clearly, detecting and locating oscillations leads to a more reliable power system operation. Figure 10 gives a summary of papers that studied forced oscillations. As it can be seen, 6 papers studied the detection methods [7, 17, 23, 29,30,31], 8 papers studied the location of forced oscillations [23, 38,39,40,41,42,43,44], 5 papers studied the effects of forced oscillations on mode estimation algorithms[5, 9, 47,48,49] and just 3 papers focused on oscillation classification [33, 34, 36]. Although it is very important to distinguish oscillations, there are not many methods to address this issue.
Beyond the previously existing methods to locate and detect forced oscillations, many future opportunities exist such as:
-
1)
The relation between length of data and magnitude of PSD, as it has been shown in Figs. 3, 4 and 5, can be used to distinguish different types of oscillations.
-
2)
As it has been discussed throughout the paper, coherence analysis has shown promising results in detecting the forced oscillations. However, there is still some deficiency in the proposed algorithms. Applying other algorithms and improving existing algorithms can be critical for detecting forced oscillations.
-
3)
Effects of data length on PSD estimation to detect the forced oscillations.
-
4)
Comprehensive study to reveal the advantage and disadvantage of different algorithms to estimate the coherence spectra for detecting oscillations.
-
5)
Distinguishing free and forced oscillations using their distinct features.
-
6)
Combination of coherence and self-coherence for a system to monitor the propagation of the information on oscillation and to locate the sources of forced oscillations.
-
7)
PMUs are installed throughout systems. They carry different information based on their location, so their distinct characteristics can be used to detect and locate the oscillations. For example, coherence amplitude and phase differences of PMU data can be used to locate the forced oscillation’s location.
-
8)
One of the important issues in power systems is the placement of PMUs. Because PMU data can be used to locate the disturbance source of forced oscillations, it can be a factor for designing a PMU placement algorithm. For example, some new constraints can be added to the optimization problem of PMU placement to including the considerations of locating forced oscillations.
8 Conclusion
This paper presented a comprehensive overview of the forced oscillations in power systems. Basically five major areas are discussed: ➀ the source of forced oscillations; ➁ detecting methods for forced oscillations; ➂ distinguishing methods of forced oscillations; ➃ locating methods for forced oscillations; ⑤ the impact of forced oscillations on power systems. In addition, future opportunities to study forced oscillations are discussed. It can be concluded that in a large power system, GCEs (such as PSS and AVR) are often reported as the sources of forced oscillations in recent years. As it has been reported, the resonance between forced oscillations and electromechanical modes can cause catastrophic events. In addition, forced oscillations in a power system have negative impacts on mode estimation algorithms. Thus, they should be detected and located in their early stage.
There is a need for a comprehensive algorithm which distinguishes forced oscillations from free oscillations and to locate the sources of forced oscillations accurately in a large and complex power system.
References
Kosterev DN, Taylor CW, Mittelstadt WA (1999) Model validation for the August 10, 1996 WSCC system outage. IEEE Trans Power Syst 14(3):967–979
Venkatasubramanian V, Li Y (2004) Analysis of 1996 western American electric blackouts. In: Proceedings of Bulk power system dynamics and control-VI, Cortina d’Ampezzo, Italy, pp 22–27
Zhou N, Huang Z, Tuffner F, Jin S, Lin J, Hauer M (2010) Final project report oscillation detection and analysis [online]. uc-ciee.org/downloads/ODA_Final_Report.pdf
Trudnowski DJ, Pierre JW (2009) Overview of algorithms for estimating swing modes from measured responses. In: 2009 IEEE Power Energy Society General Meeting (PES ’09), pp 1–8
Vanfretti L, Dosiek L, Pierre JW et al (2011) Application of ambient analysis techniques for the estimation of electromechanical oscillations from measured PMU data in four different power systems. Eur Trans Electr Power 21(4):1640–1656
Ness JV (1966) Response of large power systems to cyclic load variations. IEEE Power Appar Syst 7:723–727
Follum J, Pierre JW (2013) Initial results in the detection and estimation of forced oscillations in power systems. In: Proceedings of 2013 North American Power Symposium, pp 1–6
Vournas C, Krassas N (1991) Analysis of forced oscillations in a multimachine power system. Control 2:443–448
Myers RB, Trudnowski DJ (2013) Effects of forced oscillations on spectral-based mode-shape estimation. In: Proceedings of IEEE Power Energy Society General Meeting
Pinneilo JA, Ness JEV (1971) Dynamic response of a large power system to a cyclic load produced by a nuclear accelerator. IEEE Trans Power Appar Syst 90(4):1856–1862
Rao K (1988) Studies on power systems that are subjected to cyclic loads. IEEE Trans Power Syst 3(1):31–37
Reddy PB, Hiskens IA (2005) Limit-induced stable limit cycles in power systems. In: Proceedings of 2005 IEEE Russia Power Tech, pp 1–5
Wang X, Li X, Li F (2010) Analysis on oscillation in electro-hydraulic regulating system of steam turbine and fault diagnosis based on PSOBP. Expert Syst Appl 37(5):3887–3892
Magdy MA, Coowar F (1990) Frequency domain analysis of power system forced oscillations. In: IEE proceedings C (Generation, transmission and distribution), vol 137. IET Digital Library, pp 261–268
Rostamkolai N, Piwko R (1994) Evaluation of the impact of a large cyclic load on the LILCO power system using time simulation and frequency domain techniques. IEEE Power Syst 9(3):1–6
Hauer JHJ (1996) Extending the realism of planning models for the western north america power system. In: Proceedings of Symposium of Specialists in Electric Operational and Expansion Planning
Zhou N, Dagle J (2015) Initial results in using a self-coherence method for detecting sustained oscillations. IEEE Trans Power Syst 30(1):522–530
Kimt K, Schattlertt H, Venkatasubramanianttt V et al (1997) Methods for calculating oscillations in large power systems. IEEE Power Syst 12(4):1639–1648
Sarmadi SAN, Venkatasubramanian V, Salazar A (2016) Analysis of November 29, 2005 western American oscillation event. IEEE Trans Power Syst 31(6):5210–5211
Venkatasubramanian MV, Carroll JR (2008) Oscillation monitoring system. In presentation at NASPI meeting, Charlotte, NC
Silverstein A (2015) Diagnosing equipment health and misoperations with PMU data, North American synchrophasor initiative (NASPI), NASPI technical report [online]. https://www.naspi.org/sites/default/files/reference_documents/14.pdf?fileID=1530
Wan YH (2013) Synchronized phasor data for analyzing wind power plant dynamic behavior and model validation. Contract 303:275–3000
Sarmadi SAN, Venkatasubramanian V (2015) Inter-area resonance in power systems from forced oscillations. IEEE Trans Power Syst 31(1):378–386
Maslennikov S (2016) Locating the source of sustained oscillations. In: Presentation slide, WECC, JSIS meeting, Salt Lake City
Zhou N (June 2013) Spectral analysis of power grid PMU data. In: DOE/OE transmission reliability program, Washington, DC
Cano EB (March 2014) NYISO case studies of system events analysis using PMU data. In: Proceedings of NASPI work group meeting, Knoxville, TN
Donahoo A (2016) Oscillation detection monitor. In: Proceedings of WECC, JSIS meeting, Salt Lake City, USA
Kay SM (1998) Fundamentals of Statistical signal processing. Prentice Hall PTR, Englewooed Cliffs
Zhou N (2013) A coherence method for detecting and analyzing oscillations. In: Proceedings of IEEE Power Energy Society General Meeting, pp 1–5
Ghorbaniparvar M, Zhou N (2015) Bootstrap-based hypothesis test for detecting sustained oscillations. In: Proceedings of Power & Energy Society General Meeting, 2015, IEEE. pp 1–5
Ghorbaniparvar M, Zhou N, Li X (2016) Coherence function estimation with a derivative constraint for power grid oscillation detection. In: Proceedings of 2016 IEEE Global Conference on Signal and Information Processing (GlobalSIP), pp 791–795
Sarmadi SAN, Venkatasubramanian V (2014) Electromechanical mode estimation using recursive adaptive stochastic subspace identification. IEEE Trans Power Syst 29(1):349–358
Liu J, Yao W, Wen J et al (2014) Active power oscillation property classification of electric power systems based on SVM. J Appl Math. doi:10.1155/2014/218647
Xie R, Trudnowski D (2015) Distinguishing features of natural and forced oscillations. In: Proceedings of Power & Energy Society General Meeting, 2015, pp 1–5
Chow J (1991) Power system toolbox version 2.0: dynamic tutorial and functions. Cherry Tree Scientific Software, RR, 5
Wang X, Turitsyn K (2016) Data-driven diagnostics of mechanism and source of sustained oscillations. IEEE Trans Power Syst 31(5):4036–4046
Liu G, Venkatasubramanian V (2008) Oscillation monitoring from ambient PMU measurements by frequency domain decomposition. In: Proceedings of the IEEE international symposium on circuits and systems, pp 2821–2824
Ma J, Zhang P, Fu HJ et al (2010) Application of phasor measurement unit on locating disturbance source for low-frequency oscillation. IEEE Trans Smart Grid 1(3):340–346
Chen L, Min Y, Hu W (2013) An energy-based method for location of power system oscillation source. IEEE Trans Power Syst 28(2):828–836
Ying L, Chen S, Feng L (2012) An energy-based methodology for locating the source of forced oscillations in power systems. In: Proceedings of 2012 IEEE international conference on power syst. technol. (POWERCON), pp 1–6
Gao Y, Liu D, Huang G et al (2012) Locating method of disturbance source of forced power oscillation based on prony anyasis. In: Proceedings of China international conference on electricity distribution, pp 1–4
Li Z, Fang Y, Li W et al (2012) Forced power oscillation analysis based on EEAC theory. In: 2012 Asia-Pacific Symposium on Electromagnetic compatibility (APEMC). IEEE, pp 833–836
Yu Y, Min Y, Chen L et al (2011) The disturbance source identification of forced power oscillation caused by continuous cyclical load. In: Proceedings of DRPT 2011–2011 4th international conference on electr. util. deregul. restruct. power technol., pp 308–313
Hu W, Lin T, Gao Y et al (2011) Disturbance source location of forced power oscillation in regional power grid. In: Proceedings of the 2011 IEEE power eng. autom. conf. (PEAM 2011), pp 363–366
Zhou N, Huang Z, Dosiek L et al (2009) Electromechanical mode shape estimation based on transfer function identification using PMU measurements. In: Proceedings of Power & Energy Society General Meeting, pp 1–7
Kundur P (1994) Power system stability and control. McGraw-Hill, New York
Vanfretti L, Bengtsson S, Aarstrand VH et al (2012) Applications of spectral analysis techniques for estimating the Nordic grid’s low frequency electromechanical oscillations. IFAC Proc Vol 45(16): 1001–1006
Vanfretti L, Bengtsson S, Peric VS et al (2013) Spectral estimation of low-frequency oscillations in the Nordic grid using ambient synchrophasor data under the presence of forced oscillations. In: Proceedings of 2013 IEEE grenoble conf. PowerTech, POWERTECH, pp 1–6
Vanfretti L, Bengtsson S, Peric VS et al (2012) Effects of forced oscillations in power system damping estimation. In: Proceedings of the IEEE int. work. appl. meas. power syst. (AMPS 2012), pp 59–64
Jabbar M, Ghorbaniparvar H (2014) Determination of volatile components in black cardamom with gas chromatography-mass spectrometry and chemometric resolution. Int J Eng Res Technol 3(11)
Jabbar M, Ghorbaniparvar H (2014) Use of GC-MS combined with resolution methods to characterize and to compare the essential oil components of green and bleached cardamom. IJRCE 5
Sidorov DN, Grishin YA, Šmádl V (2010) On-line detection of inter-area oscillations using forgetting approach for power systems monitoring. In: Proceedings of 2010 The 2nd International Conference on Computer and Automation Engineering, Singapore, pp 292–295
Acknowledgements
This work was supported by the funding from State University of New York.
Author information
Authors and Affiliations
Corresponding author
Additional information
CrossCheck date: 20 September 2016
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
GHORBANIPARVAR, M. Survey on forced oscillations in power system. J. Mod. Power Syst. Clean Energy 5, 671–682 (2017). https://doi.org/10.1007/s40565-017-0273-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40565-017-0273-4