1 Introduction

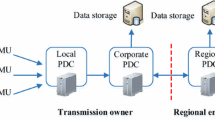
In the past decade, an increasing number of synchrophasor systems have been employed around the world, and a variety of synchrophasor applications have been implemented in power grids [1]. These synchrophasor systems and applications make use of advanced information and communication technologies (ICTs), such as the global positioning system (GPS), phasor measurement unit (PMU), phasor data concentrator (PDC), and high-speed dedicated communications as shown in Fig. 1, with the aim of enabling wide-area monitoring, protection and control and enhancing the overall performance of power grids. To realize these great potentials, efficient measurement and communication systems are demanded [1–6].

Fig. 1
figure 1

A typical synchrophasor system

Full size image

However, the actual measurement and communication systems inevitably involve data quality issues. For instance, a measurement device may cause a data accuracy issue because of device errors or timing signal loss [7], and a communication link may induce data loss and latency issues due to unintentional reasons (e.g., equipment malfunctions and communication infrastructure limits) or intentional cyber-attacks [8, 9]. These data quality issues may impact or even disable certain application functionalities. Consequently, a great deal of research effort in academia and industry has been devoted to addressing the data quality issue, especially the data accuracy, latency, and loss issues.

First, the data accuracy issue primarily derives from measurement equipment and devices, such as instrument transformers and PMUs. Conventional instrument transformers have inherent limitations on high-voltage measurement and isolation; while classic PMUs using discrete-Fourier-transform algorithms have a low computational burden but their accuracy degrades in the presence of frequency offsets and dynamic conditions. Accordingly, advanced instrument transformers like electronic instrument transformers [10, 11] and alternative PMUs using sophisticated measurement algorithms [12–14] have been developed. Those approaches greatly improve the synchrophasor measurement accuracy under both steady-state and dynamic conditions.

Second, for the data latency, the previous researches primarily focus on three aspects 1) modeling the communication delay in theoretical and statistical perspectives, such as constant modeling, stochastic modeling, and bounded modeling [8, 15], 2) developing special protection schemes and control strategies with the consideration of latencies [15–19], and 3) optimizing the communication infrastructure, like communication architecture, medium, and protocols, and restricting the communication delay to an acceptable range [20–25]. Those design and approaches have been selectively used in wide-area protection & control and other advanced applications.

Further, for the data incompleteness and missing, numerous researches work on reducing the risk of data loss, such as the ones enhancing communication performance in terms of communication architecture, bandwidth, and redundancy [21–27]. In addition, some researches deal with the data loss issue in a positive way. For example, a predictive control strategy for wide-area damping control was presented in [28] with the consideration of data loss and other physical constraints, and a data reconstruction method using the low-rank matrix completion approach was provided in [29], in which way the lost data could be partially recovered at a control center.

This work studies the data quality issue for synchrophasor applications. In Part I, the data quality issue is reviewed in a comprehensive way and in Part II the potential reasons and solutions for the data quality issue are investigated. Specifically, Part II pays particular attention to synchronization signal loss and synchrophasor data loss events. For the former, the historical timing signal loss events are analyzed and the potential reasons and solutions are discussed. For the latter, the synchrophasor data loss, especially the scenario of a small amount of synchrophasor data loss, is studied, and the possible estimation methods like substitution, interpolation, and forecasting methods are examined. The estimation methods can improve the accuracy and availability of synchrophasor measurements, and mitigate the effect of data loss on synchrophasor applications.

2 Synchronization signal loss

Accurate and reliable synchronization signals play a critical role in synchrophasor systems. They provide the common timing reference for data measurement and synchronization, and largely determine the accuracy and availability of synchrophasor data. However, according to the statistics in Part I, a large number of PMUs and FDRs experienced timing signal loss (i.e. GPS signal loss). The potential reasons and solutions are explored in this section.

2.1 Potential reasons

Theoretically, the GPS signal availability, especially the strength, might be affected by two factors: the weather and the surrounding of GPS antennas.

The weather events primarily refer to the ionospheric scintillation and solar radio burst, which can degrade GPS signal performances [30]. In particular, the strongest scintillation normally occurs at the equatorial regions. This means more interference signals will be applied to the GPS antenna located in the low latitude [31].

In order to investigate the impact of weather events on GPS signal loss, two studies are performed. First, the average yearly GPS-signal-loss events of the FDR from 2010 to 2012 are counted. As shown in Fig. 2, the GPS-signal-loss events of all FDRs across North America are depicted in the spatial manner, while no clear geological pattern is identified from the historical data. Second, the average monthly GPS-signal-loss events of the FDR from 2010 to 2012 are calculated as shown in Fig. 3, and the historical solar activities from 2010 to 2012 are reviewed (it is reported that the largest solar activity happened on March 7, 2012 00:24 UTC - the sun unleashed an X5.4-class solar flare) [32]. By comparing the trend in Fig. 3 and the trend in reference [32], no obvious relationship between GPS signal loss and solar radio bursts is found. These two studies imply that the overall GPS signal availability is not significantly affected by the weather.

Fig. 2
figure 2

Spatial distribution of GPS signal loss in North America

Full size image
Fig. 3
figure 3

Temporal distribution of GPS signal loss from 2010 to 2012

Full size image

In addition, the GPS signal availability is also affected by the surrounding of GPS antennas [33]. For example, an FDR is usually installed indoor with a directional GPS antenna instead of an omnidirectional GPS antenna. The performance of the antenna or antenna reception may be affected by the surrounding. For instance, whether the antenna is installed near a window with an open view to the sky, and whether the antenna reception is located nearby the buildings or obstacle that frequently reflect or block GPS signals.

2.2 Potential solutions

To improve the accuracy and availability of GPS signals, the performance of GPS receivers should be considered first. For instance, if a PMU uses an on board GPS receiver, the PMU can parse the GPS signal strength information, e.g., the number of locked satellites from a GPS receiver, and further track the GPS signal strength; and if a PMU uses GPS signals as synchronization signals, the GPS signal strength can be enhanced through installing omnidirectional antenna on the roof with the open sky.

Note that the antenna type will impact the GPS signal availability. Directional antennas transmit and receive signals in a particular direction, so they are generally subject to a particular reception pattern (e.g., they would lower the signal availability when the directional path is affected). In contrast, omnidirectional antennas transmit and receive signals in all horizontal directions, enabling users to use the GPS antenna without concerning the antenna’s reception pattern. Therefore, omnidirectional antennas can improve reception in such terrains where directional path would be affected.

Some emerging data analytics solutions can also improve the timing accuracy of synchrophasor measurements. For the lost or drifted timing signals, the context data in the time range with available and accurate timing, or the data from other units, can help reconstruct the missing information. Data interpolation and data realignment tools also provide the possibility to patch the timestamp or shift the data back to its correct position [34].

Moreover, since the availability of GPS signals is difficult to be guaranteed, some backup synchronized timing sources can be used, such as network time protocol (NTP), e-Loran, and chip scale atomic clock (CSAC). Several backup synchronized timing technologies have been employed for synchrophasor measurement. It is demonstrated that they provide ultra-high timing accuracy and reliability to meet IEEE Standards [7], [35–37].

3 Synchrophasor data loss

As discussed in Part I, a number of synchrophasor applications (e.g., Class-A applications) prefer accurate and complete synchrophasor data. The data loss issue may lower and even disable the performances of certain synchrophasor applications [4]. The incomplete or missing data can make the power grid unobservable and vulnerable, and even aggravate the cascading effects in large-scale blackouts [28], [38]. PMU Application Requirements Task Force at North American Synchrophasor Initiative (NASPI) has been working on standardizing and quantifying the requirements of synchrophasor applications [39].

To address the data loss issue, several advanced data recovery techniques were proposed in the literature [25, 29]. Those data recovery techniques are applicable for off-line applications but indeed costly for the majority of real-time applications. Moreover, as discovered in Part I, about 95% data loss events involve only one to three lost packages and a large amount of data loss is a small probability event. Hence, this paper focuses on the scenario of a small amount of package losses, and examines a set of estimation methods to mitigate the corrupted and missing data, including substitution, interpolation, and prediction.

3.1 Lagrange interpolating polynomial method

Currently, there is no standardized method to address the issue of synchrophasor data loss. Most commercial PDCs use the substitution method, in which the lost data are simply set to zero. Obviously, this method will lower the data accuracy and completeness. One alternative method is interpolation, and a Lagrange interpolating polynomial method is presented below [40].

In general, the Lagrange polynomial L(x) passes through a set of given data points (x 1, y 1) = f(x 1), (x 2, y 2) = f(x 2), …, (x n , y n ) = f(x n ), and other points can be approximatively calculated with

$$L(x) = \sum\limits_{j = 1}^{n} {y_{j} \cdot \ell_{j} (x)} = \sum\limits_{j = 1}^{n} {y_{j} } \cdot \mathop \prod \limits_{\begin{subarray}{l} k = 1 \\ k \ne j \end{subarray} }^{n} \frac{{x - x_{k} }}{{x_{j} - x_{k} }}$$
(1)

where \(\ell_{j} (x)\) is the coefficient in the Lagrange polynomial.

Considering the trade-off between algorithm accuracy and hardware-cost, n is selected as 3 and (1) can be rewritten as the quadratic interpolation in (2).

$$L(x) = y_{1} \frac{{(x - x_{2} )(x - x_{3} )}}{{(x_{1} - x_{2} )(x_{1} - x_{3} )}} + y_{2} \frac{{(x - x_{1} )(x - x_{3} )}}{{(x_{2} - x_{1} )(x_{2} - x_{3} )}} + y_{3} \frac{{(x - x_{1} )(x - x_{2} )}}{{(x_{3} - x_{1} )(x_{3} - x_{2} )}}$$
(2)

The first case assumes only one synchrophasor package is lost. The simple lost data can be estimated with the quadratic interpolation in (2). Also, since only three points are required in the estimation, the lost data can be further estimated with the weighted interpolation. For instance, the lost point v 4 as shown in Fig. 4a can be calculated with (2) in the following ways

$$\left. {\hat{v}_{4} } \right|_{1,2,3} \,=\, v_{1} - 3v_{2} + 3v_{3}$$
(3)
$$\left. {\hat{v}_{4} } \right|_{2,3,5} \,=\, - \frac{1}{3}v_{2} + v_{3} + \frac{1}{3}v_{5}$$
(4)
$$\left. {\hat{v}_{4} } \right|_{3,5,6}\, =\, \frac{1}{3}v_{3} + v_{5} - \frac{1}{3}v_{6}$$
(5)
$$\left. {\hat{v}_{4} } \right|_{5,6,7} \,=\, 3v_{5} - 3v_{6} + v_{7}$$
(6)
$$\hat{v}_{4} \,=\, c_{1} \left. {\hat{v}_{4} } \right|_{1,2,3} \,+\, c_{2}\left. {\hat{v}_{4} } \right|_{2,3,5} \,+\, c_{3} \left. {\hat{v}_{4} } \right|_{3,5,6} \,+\, c_{4} \left. {\hat{v}_{4} } \right|_{5,6,7}$$
(7)

where c 1, c 2, c 3 and c 4 are the coefficients in the weighted interpolation. The average weights are used here since their practicality and simplicity.

Fig. 4
figure 4

Synchrophasor data loss with different conditions

Full size image

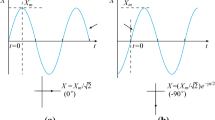
The special condition as depicted in Fig. 4b is considered, in which the first or last package in a dataset is lost. In this case, the estimates can be calculated with the polynomial extrapolation in (8) and (9), respectively.

$$\hat{v}_{1} = 3v_{2} - 3v_{3} + v_{4}$$
(8)
$$\hat{v}_{7} = v_{4} - 3v_{5} + 3v_{6}$$
(9)

The second case considers the continuous package loss and the lost data can be estimated with the extrapolation as well. For instance, the three points as shown in Fig. 4c are lost and they can be recursively estimated as follows

$$\hat{v}_{4} = v_{1} - 3v_{2} + 3v_{3}$$
(10)
$$\hat{v}_{5} = v_{2} - 3v_{3} + 3\hat{v}_{4}$$
(11)
$$\hat{v}_{6} = v_{3} - 3\hat{v}_{4} + 3\hat{v}_{5}$$
(12)

Note that the extrapolation assumes the data are smooth and performs poorly for the dramatically changing data. Also, a maximum package loss amount is normally preset in power system engineering, and an alarm will arise when the actual package loss number exceeds the maximum amount.

In addition, the practical synchrophasor package may be lost discontinuously and randomly, and they can be compensated with the interpolation and extrapolation collectively. A simple example is presented in Fig. 4d and the discontinuous points can be calculated as follows

$$\hat{v}_{3} = \frac{1}{3}v_{2} + v_{4} - \frac{1}{3}v_{5}$$
(13)
$$\hat{v}_{6} = \hat{v}_{3} - 3v_{4} + 3v_{5}$$
(14)
$$\hat{v}_{7} = v_{4} - 3v_{5} + 3\hat{v}_{6}$$
(15)

Here, the 3nd point in Fig. 4d can be further estimated with the weighted interpolation, in which the estimation accuracy is expected to improve. Also, the estimation errors in above estimations are unavoidable and can be expressed as

$$E(x) = f(x) - L(x) = \frac{{f^{(n)} (\xi )}}{3!} \cdot \prod\limits_{k = 1}^{3} {(x - x_{k} )}$$
(16)

Further, for the current and voltage with harmonics as \(v_{k} = v_{0} + \sum\limits_{h = 1}^{\infty } {v_{h} {\sin} {\textit{(}}h\omega t + \varphi_{h} {\textit{)}}}\) the related estimation error can be written as

$$E(t) \le \frac{{\omega^{3} }}{3{\textit{!}}}\sum\limits_{h = 1}^{\infty } {(v_{h} h^{3} )} \left| {\prod\limits_{j = 1}^{3} {(t - t_{j} )} } \right|$$
(17)

Typically, for the rate of change of frequency (ROCOF) or frequency measurement, its accuracy is evaluated with absolute errors (e.g., frequency error Hz or ROCOF error Hz/s), while for the phasor measurement, its accuracy is evaluated with the total vector error (TVE) as

$${{TVE}}(n) = \sqrt {\frac{{(\hat{X}_{r} (n) - X_{r} (n))^{2} + (\hat{X}_{i} (n) - X_{i} (n))^{2} }}{{(X_{r} (n))^{2} + (X_{i} (n))^{2} }}}$$
(18)

where X r (n) and X i (n) are the sequences of theoretical values of the input signal at the instant of time (n), and \(\hat{X}_{r} (n )\) and \(\hat{X}_{i} (n )\) are the sequences of estimates. The TVE of P class and M class PMUs is required to be less than 1% in steady-state in IEEE Standard C37.118.

3.2 Forecasting method

In addition to the substitution and interpolation, the prediction is also widely used in data estimation [41, 42]. Here, the synchrophasor data are viewed as an observed time series driven by a stochastic process and represented by a state equation and a measurement equation as follows:

$$x_{k + 1} = A_{k} x_{k} + B_{k} \omega_{k}$$
(19)
$$y_{k} = C_{k} x_{k} + D_{k} v_{k}$$
(20)

where x k+1 is the state that characterizes the measurement y k ; it is a variable of the time series determined by the previous state x k and the noise term ω k introduced at each k. A k , B k , C k and D k denote the corresponding coefficients.

The unknown system parameters θ k  = {A k , B k , C k , D k } and states {x k } can be estimated through a finite set of received signal measurement data {y 1, y 2, …}. Also, the parameters in (19) and (20) are estimated using the prediction error minimization (PEM) algorithm here, with the objective of minimizing prediction errors. The PEM updates the measurement set every time when the new measurement comes in, such that the whole model is updated with the new measurement set to keep up with time-varying parameters [42]. The PEM algorithm estimates the system parameters by minimizing a least square cost function as follows:

$${\min}\,J_{N} = {\min} \frac{1}{N}\sum\limits_{k = 0}^{N - 1} {\|{y_{k} - \hat{y}_{k} }\|_{2}^{2}}$$
(21)

When the lost synchrophasor data are treated as the synchrophasor data in future, they can be recursively predicted on the basis of the previous states and estimated parameters. In particular, the PEM algorithm employs a finite number of stored measurements for the next prediction where the store size can be chosen as small as the algorithm has a solution. Thus, different from the widely used artificial neural networks based prediction approaches which require large historical data for data modeling and training [43], the presented prediction method results in acceptable hardware cost and it is applicable for the data estimation of on-line applications [4, 9, 39].

4 Simulation results

In order to demonstrate the performance of the proposed methods, the simulation with MATLAB is performed here. Because the power system data may vary regularly in normal operation but dramatically change in a fault or disturbance, the real PMU data in a fault event are used as inputs as shown in Fig. 5. Because of the limited space, three groups of twenty samples are selected from the pre-fault, in-fault, and post-fault states in Fig. 5 and further used as the test data as shown in Fig. 6.

Fig. 5
figure 5

PMU data profile in one minute

Full size image
Fig. 6
figure 6

Test data in diverse conditions

Full size image

4.1 Substitution and interpolation based estimation

The substitution and the interpolation based estimation methods are tested. First, three sets of twenty samples in Fig. 6 representing the different conditions in power grids are used as test inputs. Then, the 5th, (5th, 6th), (5th, 6th, 7th), …, (5th, …, 14th) samples are manually set lost, and the proposed weighted interpolation method with different times of estimation (e.g., two times and three times of estimation) is applied to estimate the lost data. The corresponding simulation results are presented in Fig. 7.

Fig. 7
figure 7

Simulation results of the weighted interpolation method

Full size image

Note that this paper focuses on the scenario of a small amount of synchrophasor data loss and the simulation studies the scenario of one to ten continuous package losses. The twenty samples are good enough for the maximum continuous package losses.

For the substitution, the lost sample is treated as “zero” and its TVE sharply increases to 100%. Hence, the continuous data loss will lower the accuracy of synchrophasor data and even lead to the malfunction of certain synchrophasor applications [4].

For the interpolation, it is observed that in the pre-fault and post-fault states, the lost data can be efficiently estimated (TVE <1%), whereas in the faulty state, the estimation error is acceptable only in the scenario of one or two continuous package losses.

Moreover, the estimation accuracy is improved by the weighted interpolation, e.g., the three times estimation generally presents lower TVE than the one time estimation. The estimation accuracy is also affected by the nature of synchrophasor data, e.g., the TVE of the scenario of nine continuous data loss in Fig. 7b suddenly drops to 1% since the data changes gently in this field. Therefore, the proposed interpolation method can adaptively estimate the missing data in different conditions, and the estimation results are acceptable in the scenario of the small amount of data loss.

Further, the proposed Lagrange interpolating polynomial algorithm only includes simple addition and multiplication as shown in (2)–(15), which can be embedded in a lookup table. Thus, the proposed interpolation method can be efficiently employed in a PDC in practice.

4.2 Prediction based estimation

The perdition method with the same inputs in Fig. 6b, c is tested as well. It is observed from the simulation results in Figs. 8 and 9 that the prediction method can estimate the lost data with high accuracy, while a bit high prediction error still exists in the scenario of continuous data loss and/or dynamic data changes.

Fig. 8
figure 8

Simulation results of the prediction method

Full size image
Fig. 9
figure 9

TVE results of the prediction method

Full size image

For example, for the voltage angle values in Fig. 8b, d, the high prediction accuracy is obtained for the voltage angle varying in a small range whereas the high prediction errors happen to certain voltage angles dynamically changing.

According to the above analysis, a brief review of the three estimation methods is provided in Table 1. The interpolation method presents comparable estimation accuracy as the prediction method but requires less hardware cost. Therefore, the interpolation method achieves the trade-off between accuracy and complexity. It is favorable for the estimation of the corrupted and missing synchrophasor data.

Table 1 Brief review of the three estimation methods
Full size table

5 Conclusions

A number of synchrophasor applications prefer accurate, complete, and timely data, and their performances may be impacted or even disabled due to data quality issues. This paper investigates the data quality issue for synchrophasor applications and pays particular attention to the synchronization signal loss and synchrophasor data loss events.

First, the historical synchronization signal loss events are analyzed, and the potential reasons and solutions are discussed. It is found that a large number of PMUs and FDRs experienced GPS signal loss, and this issue might get worse under the bad weather and surrounding. It is advantageous to optimize the location of GPS antennas and deploy advanced ICTs and backup schemes.

Second, the issue of synchrophasor data missing and incomplete is studied. For the off-line applications, the missing data can be processed in the control center with advanced information recovery techniques; while for the real-time applications, the incomplete data normally are directly delivered to the applications, which is unfavorable for certain applications.

Further, it is observed from the statistics in Part I that about 95% data loss events involve only one to three lost packages. Hence, this paper focuses on the scenario of a small amount of synchrophasor data loss and proposes the estimation method with Lagrange interpolating polynomial algorithms. Compared with the substitution and the prediction methods, the interpolation method can estimate the lost data in diverse conditions adaptively and achieve the trade-off between accuracy and complexity. Moreover, the interpolation method requires simple calculations only, and thus can be embedded in a lookup table and employed efficiently in a practical PDC.

Future works may include the optimization of the interpolation method (e.g., the coefficients) and the implementation of the data estimation method in real PDCs.