1 Introduction

With the overwhelming importance that sustainability has gained in recent time, it is vital for the significant entities of global emissions like transportation and power generation to abridge their emissions keeping in mind the end goal to cut down them to 80% by 2050 [1], thereby accomplishing the goals set in endorsing Kyoto Protocol launched by United Nations Framework Convention on Climate Change (UNFCCC) [2]. Subsequently, the transportation and electricity sectors have committed to promoting green alternatives by exploiting the potential benefits of non-conventional, renewable and electric vehicle resources in every possible direction for a sustainable future.

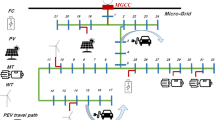
Electric power utilities around the globe witnessing whole modernization and rebuilding lately, because of the developing smart grid innovations [3]. One of the real strengths driving this pattern is the combination of renewable energy technologies (RET) into power generation. Unit commitment (UC) is a traditional problem in the electric network which empowers effective asset planning at least cost, yet fulfilling all the network and system constraints [4]. Renewable energy joining with the current customary fossil fuel plants has prompted revolutions in the power sector [5] in heading towards sustainable development. Wind energy asset with high penetration was planned along thermal units to cut down emissions [6]. Lately, backed by the cost effective manufacturing process and fiscal policy implications around the world, solar photovoltaic energy was also considered on short-term scheduling basis [7]. Because of the way that renewable energy brings in instability into the framework, it is essential to consider the reliability before incorporating them into the framework. In the UCP with strict limitations like load fulfilment and other reliability issues (system reserve, stability and regulation, etc.) handling the uncertainty through either accurate forecasting methods or suppressing the variability by employing storage technologies is a key prospect [8].

As a result of electrification of the transportation sector, the stress on the existing electric network is likely to change with charging demands of the plug-in electric vehicles (PEV) [9]. However, intelligent handling of the PEVs in conjunction with the utility resources like thermal units and RETs can minimize the cost and burden of the network [10]. In addition, the coordination of RETs with PEVs in which part or entire PEV charging load is supplied by RET has been in practice to reduce network congestion, cost and emissions into environment [11].

Over the past decade, various optimization techniques have been proposed by various researchers to solve the UCP. Techniques like branch and bound method (BBM), dynamic programming (DP), priority list (PL), mixed integer linear programming (MILP) and Lagrangian relaxation (LR) algorithms are developed to solve the UCP. On the other hand, each methodology has its qualities and confinements. Among these optimization techniques, PL offers straightforwardness and slightest computational time, however a tradeoff must be made with the solution quality [12]. With DP, absence of adaptability and expanded calculation time at higher measurement ends up being the disadvantageous in executing UCP for wide range, large number of thermal units [13]. While, exponentially aggravating computational time system dimension hampers the use of MILP and BBM techniques for UCP in large systems [14]. Finally, when executed with LR, UCP being a non-convex optimization technique, prompts troubles in determination of feasible global solution [15].

Lately, heuristic optimization approaches became extremely well known because of their effortlessness and proficiency in global minimum search. In the past studies, genetic algorithm (GA) is developed by observing the processes of reproduction, natural selection and mutation in animals and utilized to tackle UCP [16]. Additionally, hybrid variations with combinations of different algorithms like LRGA are devised to reduce the search space thereby making the search for optimal search effective [17]. Thereupon, inspired by swarm intelligence like social behavior and coordination principles, particle swarm optimization (PSO) is proposed and developed to improve the quality of UCP solution [18]. Further, to allocate ON/OFF status of thermal units distinctive varieties of PSO like binary particle swarm optimization (BPSO), quadratic binary particle swarm optimization (QBPSO), improved binary particle swarm optimization (IBPSO) is proposed for UCP [19–21]. Afterwards, algorithms like ant colony optimization (ACO) deduced from the natural behavior of ants in discovering the shortest path looking for food, are exploited in successful handling of commitment and scheduling of thermal units to minimize the generation cost [22].

Recently, by mimicking particular behavior of firework display in the sky, fireworks algorithm (FWA) is proposed [23]. In this algorithm, fireworks are comprehensively partitioned into two sorts, good and bad fireworks in view of the explosion and associated sparkles. The firework explosion with good cluster giving a spectacular display is characterized as a good firework and vice versa. The basic idea behind the fireworks assumes the area spread by the sparks associated with a firework explosion represents the search space. Therefore, a good firework with closely associated sparks all around symbolizes an effective search space with a higher probability of optimal solution, and a bad firework with distant sparks in the larger area represents ineffective search space. Hence, on observing the better performance of FWA over other existing techniques regarding convergence and optimal search for benchmark problems, authors would like to expand its application to complex optimization problem like UCP through a binary variant of FWA.

2 Problem formulation

The UCP is an optimization problem in which for the given load and available generation units, the total operational cost is minimized by intelligent commitment and optimal power allocation under specified network and unit constraints. In this paper, short-term power scheduling of thermal units is carried out for 24 hours. The operational cost includes fuel and startup costs, also, incorporates system constraints like load balance, reserve and units constraints like up/down ramp rates, times, generation limits etc.

2.1 Model development

2.1.1 Wind energy generator (WEG)

Variable nature of wind resource complicates the scheduling of wind energy. However, accurate prediction of wind resource and appropriate modeling can improve its accuracy [24]. In literature, there are several models postulated for wind energy generation with most appropriate one being formulation of wind energy from power curve (Fig. 1) of wind turbine [25].

Fig. 1
figure 1

Power curve of wind energy generator

Full size image

Modern wind turbines are modeled to operate in four modes namely, below cut in, linear, rated and cut-out speeds as formulated below:

$$P_{\text{weg}} \left( t \right) = \left\{ {\begin{array}{lll} {0 \, } \hfill &\quad {\text{if}}& V\left( t \right) < V_{\text{ci}} ;\;\;V_{\text{co}} < V(t) \hfill \\ {\varPsi \left( t \right)} \hfill &\quad {\text{if}} & V_{\text{ci}} < V\left( t \right) < V_{\rm r} \hfill \\ {P_{\text{wtr}} } \hfill & \quad {\text{if}} &V_{\text{r}} < V\left( t \right) < V_{\text{co}} \hfill \\ \end{array} } \right.$$
(1)

where V ci, V r, V co denote cut-in, rated and cut out speeds of wind turbine respectively which are characteristic of particular wind turbine under study and \(\varPsi \left( t \right)\) is the output power of wind turbine operating in linear region which is given by:

$$\varPsi \left( t \right) = xV(t)^{2} + yV\left( t \right) + z$$
(2)

In above equation, coefficients x, y and z are turbine specific.

2.1.2 Solar photovoltaic generation (SPV)

The power output of photovoltaic generator can be found as a function of global solar irradiance and cell temperature using the following equation [26]:

$$P_{\text{pev}} (t) = \frac{G}{{G_{\text{r}} }}P_{\text{m}} \{ 1 + \lambda (T - T_{\text{r}} )\}$$
(3)

where G is the global irradiance; P m the maximum power under standard testing conditions (STC); T the cell temperature; \(T_{\text{r}}\) the temperature at STC (25 °C); G r the global irradiance at STC (1000 W/m2); and \(\lambda\) the maximum power correction for temperature [27].

2.2 Dual objective function

Managing all type of load and distributed generation is a critical exercise. In this paper, RET and PEV are used to reduce emissions from electricity and transportation sectors. Optimization problem is a dual objective function consisting of cost and emissions:

$$F\text{(}P\text{) = }\varPhi_{\text{1}} TC + \varPhi_{\text{2}} TE$$
(4)

where TC and TE are the total operational cost, total emissions respectively; and ϕ 1, ϕ 2 are the weight factors. The total operational cost (TC) is given by:

$$TC = \sum\limits_{t = 1}^{T} {} \sum\limits_{i = 1}^{NG} {} [\{ C\left( {P(i,t)} \right)A(i,t)\} ] + \{ SC(i,t)A(i,t)\}$$
(5)

where \(A\left( {i,t} \right)\) is the binary variable representing the ON-OFF status of thermal unit \(i\) in hour \(t\); and \(C\left( {P\left( {i,t} \right)} \right)\) is the fuel cost function of \(i^{{\text{th}}}\) thermal unit for \(t^{{\text{th}}}\) hour which is given by:

$$C\left( {P\text{(}i,t\text{)}} \right) = a_{i} P\text{(}i,t\text{)}^{\text{2}} + b_{i} P\text{(}i,t\text{)} + c_{i}$$
(6)

where a i , b i and c i are the fuel cost coefficients of \(i^{{\text{th}}}\) thermal unit. For thermal units, hot start-up cost \(HSC\left( i \right)\) or cold start-up costs \(CSC\left( i \right)\) will be accounted depending upon the boiler operating characteristics as follows:

$$SC\text{(}i,t\text{)} = \left\{ {\begin{array}{*{20}l} {HSC\text{(}i\text{)},MDT\text{(}i\text{)} \le OFFh\text{(}i\text{)} \le CSh\text{(}i\text{)} + MDT\text{(}i\text{)}} \hfill \\ {CSC\text{(}i\text{)},CSh\text{(}i\text{)} + MDT\text{(}i\text{)} \le OFFh\text{(}i\text{)}} \hfill \\ \end{array} } \right.$$
(7)

where \(MDT\left( i \right)\), \(CSh\left( i \right)\) are the minimum down time (in hours), cold start hours of \(i^{{\text{th}}}\) thermal unit and \(OFFh\left( i \right)\) is the time in hours for which ith unit is in OFF state. The total emission cost is given by:

$$TE = E_{c} \left( {P\text{(}i,t\text{)}} \right) = \theta_{i} \left( {\chi_{i} P\text{(}i,t\text{)}^{\text{2}} + \beta_{i} P\text{(}i,t\text{)} + \gamma_{i} } \right)$$
(8)

where \(\theta_{i} \;\) ($/ton) is the emission penalty cost of \(i^{{\text{th}}}\) thermal unit given as:

$$\theta_{i} = \frac{{a_{i} P_{{i\text{,max}}}^{\text{2}} + b_{i} P_{{i\text{,max}}} + c_{i} }}{{\chi_{i} P_{{i\text{,max}}}^{\text{2}} + \beta_{i} P_{{i\text{,max}}} + \gamma_{i} }}$$
(9)

In order to evaluate the overall effectiveness of PEV, emissions resulting from conventional vehicle are also considered for comparison [28]. The emissions are modeled as linear approximate model given by:

$$\xi \text{(}T_{l} ,\varepsilon_{i} \text{)} = T_{l} \cdot \varepsilon_{i}$$
(10)

where \(\xi \left( \right)\) is the linear approximate function; \(T_{l}\) the transit length; and \(\varepsilon_{i}\) the emission coefficient expressed in terms of ton/mile travelled.

2.3 System constraints

2.3.1 Load balance constraint

At every point of time, the load and generation should be strictly balanced in order to assure the system frequency requirements. The total generation i.e., power dispatched from thermal units, distributed generators and PEVs has to satisfy the total system load for the hour.

$$\sum\limits_{{t\text{ = }1}}^{T} {\sum\limits_{{i\text{ = }1}}^{NG} {P\text{(}i,t\text{)} + P_{{\text{spv}}} \text{(}t\text{)} + P_{{\text{weg}}} \text{(}t\text{)} + P_{{\text{pev}}} \text{(}t\text{)} = Pl\text{(}t\text{)}} }$$
(11)

where

$$P_{{\text{pev}}} \text{(}t\text{)} = \left\{ {\begin{array}{*{20}l} { + P_{{\text{pev}}} \text{(}t\text{)}} \hfill & {\text{for}\;\text{discharging}} \hfill \\ { - P_{{\text{pev}}} \text{(}t\text{)}} \hfill & {\text{for}\;\text{charging}} \hfill \\ \text{0} \hfill & {\text{when}\;\text{EV}\;\text{is}\;\text{in}\;\text{transit}} \hfill \\ \end{array} } \right.$$
(12)

To avoid power loss of the PEV battery during charge-discharge operations, maximum charging and discharging limits are enforced as given by,

$$P_{{\text{pev}}}^{{\text{min}}} < P_{{\text{pev}}} \text{(}t\text{)} < P_{{\text{pev}}}^{{\text{min}}}$$
(13)

where \(P_{{\text{pev}}}^{{\text{min}}}\) is the maximum discharge level, and \(P_{{\text{pev}}}^{{\text{min}}}\) is the maximum charge limit of PEV.

2.3.2 Reserve constraint

The electrical system is guarded by reserve in case of contingency occurrence and generation outage as given by:

$$\sum\limits_{t = 1}^{T} {\sum\limits_{i = 1}^{NG} {GR(i,t)A(i,t) + P_{\text{spv}} (t) + } } P_{\text{weg}} (t) + P_{\text{pev}} (t) \ge RR(t)$$
(14)

where RR(t) is the required reserve for t th hour given as a percentage change in load/generation due to of probability occurrence (r)

$$RR\text{(}t\text{)} = Pl\text{(}t\text{)} \cdot \text{(1} + r\text{)}$$
(15)

and \(GR\left( {i,t} \right)\) is the reserve available from \(i^{{\text{th}}}\) thermal unit at t th hour which is given by,

$$GR\text{(}i,t\text{)} = (P_{{i,\text{max}}} - P\text{(}i,t\text{))}A\text{(}i,t\text{)}$$
(16)

where \(P_{{i\text{,max}}}^{\text{ }}\) corresponds to the maximum capacity of \(i^{{\text{th}}}\) thermal unit.

2.4 Thermal unit constraints

2.4.1 Generation limits/bounds

For every instant of time, thermal unit generation will be constricted by upper and lower generation limits as given by

$$P_{{i,\text{max}}} \le P\text{(}i,t\text{)} \le P_{{i\text{,max}}}$$
(17)

where \(P_{{i\text{,min}}}^{ }\), \(P_{{i\text{,max}}}^{ }\) are the minimum and maximum generation limits of \(i^{{\text{th}}}\) thermal unit respectively.

2.4.2 Minimum up/down times

There exists a predefined time between ON/OFF exchanging operations of a generation unit because of the thermal and mechanical limits forced by boiler operational attributes.

$$\left\{{\begin{array}{lll} (1 - A(i,t + 1))MUT(i,t) \le ONh(t),\hfill & \quad {\text{if}} & A(i,t) = 1 \hfill\\ {A(i,t + 1)MDT(i,t) \le OFFh(i),} \hfill &\quad {\text{if}} & A(i,t) = 0 \\\end{array}}\right.$$
(18)

where \(MUT\left( {i,t} \right)\) the minimum time for which the unit ought to be continued once it is committed; and \(ONh\left( i \right)\) is the number of hours from which the \(i^{{\text{th}}}\) unit is in on state and binary digits 1,0 stands for ON, OFF conditions of a thermal unit.

2.4.3 Ramp up/down rates

Considering the physical limitations in changing the generation output of a turbine ramp up/down rates are introduced at each hour in the UC problem as given by:

$$P_{i}^{{\text{min}}} \text{(}t\text{)} \le P\text{(}i,t\text{)} \le P_{i}^{{\text{max}}} \text{(}t\text{)}$$
(19)

where

$$ \left\{ \begin{aligned} P_{i}^{{\text{min}}} \text{(}t\text{)} = \text{max}\left( {\text{(}P_{i}^{{\text{min}}} \text{)},P\text{(}i,t - \text{1)} - RD_{i} } \right) \hfill \\ P_{i}^{{\text{max}}} \text{(}t\text{)} = \text{min}\left( {\text{(}P_{i}^{{\text{max}}} \text{)},P\text{(}i,t - \text{1)} - RU_{i} } \right) \hfill \\ \end{aligned}\right.$$
(20)

where \(RD_{i}\), \(RU_{i}\) are ramp down and up rates of \(i^{{\text{th}}}\) generator respectively; and \(P\left( {i,t - 1} \right)\) is the power generation of \(i^{{\text{th}}}\) plant during \(\left( {t - 1} \right)^{{\text{th}}}\) hour.

2.4.4 Initial states

At the point when committing the units for the following 24 hours the status of units at the most recent hour of earlier day must be inspected as they are prone to influence start-up costs and minimum up/down times.

3 Algorithm development

3.1 FWA overview

The optimal solution search using the FWA algorithm is a sequential process in which the explosion of the firework is followed by selection of sparks for the next explosion based on the number and distance between sparks associated with the firework explosion. The good firework selected for next round of explosion denotes the feasible optimal location of the optimization problem in the search space defined. The characteristics of the FWA which aid in selection of sparks for the next generation are given below.

3.1.1 Number of sparks

For the objective function f(x), variables x(1), x(2),⋯, x(i) denotes the number of fireworks and the number of sparks generated by \(i^{{\text{th}}}\) fireworks is given by

$$S_{i} = m\frac{{y_{{\text{max}}} - f(x_{i}) + \xi }}{{\sum\nolimits_{{i\text{ = 1}}}^{n} { (y_{{\text{max}}} - f\text{(}x_{i} \text{))}} + \zeta }}$$
(21)

where the number of created sparks from n firecrackers is controlled by parameter m, \(y_{{\text{max}}}\) indicates the most worst value of objective function max(f(x i )) acquired for n fireworks i.e., (i = 1,2,⋯,n) and the smallest constant ξ is utilized to avoid the event of zero-division-error. In order to avoid devastating effects of glorious fireworks, S i is bounded as given by

$$\hat{S}_{i} = \left\{ {\begin{array}{*{20}l} {S_{{{\rm max}^{\prime } }} } \hfill & {{\kern 1pt} {\rm if}\;S_{i} > S_{\hbox{max} } } \hfill \\ {S_{{{\rm min}^{\prime } }} } \hfill & {{\kern 1pt} {\rm if}\;S_{i} > S_{\hbox{max} } } \hfill \\ {round(S_{i} ),} \hfill & {{\kern 1pt} {\rm otherwise}} \hfill \\ \end{array} } \right.$$
(22)

3.1.2 Amplitude of explosion

The amplitude of the firework is inversely proportional to the spark number such that, a good firework with large number of sparks will have small amplitude and vice versa.

$$A_{i} = \hat{A}\frac{{f(x_{i}) - y_{{\text{min}}} + \xi }}{{\sum\nolimits_{{i\text{ = 1}}}^{n} {(f\text{(}x_{i} \text{)} - y_{{\text{min}}} )} + \xi }}$$
(23)

where \(\hat{A}\) is the maximum amplitude of explosion; and y min is the minimum value of objective function min (f(x)) obtained for fireworks (i = 1, 2,⋯, n).

3.1.3 Generation of sparks

During the explosion process, z random directions can affect the sparks associated with the explosion and the number of random directions is given by

$$z = \text{round}\left( {d.rand \text{(0,1)}} \right)$$
(24)

where d is the x location’s dimensionality and rand (0, 1) corresponds to uniform distribution with in {0, 1}. Algorithm development and implementation for the same is depicted in Algorithm 1.

Algorithm 1 Obtain the location of a spark

1.

Initialize the location of the spark: \(\widetilde{{x_{j} }} = x_{i}\)

2.

\(z\text{ = }round\left( {d.rand\left( {\text{0,1}} \right)} \right)\)

3.

Select \(\widetilde{{x_{j} }}\) of z dimension randomly

4.

Calculate displacement h = A i ·\(rand\left({- 1,1} \right)\)

5.

For each dimension of \(\widetilde{{x_{k}^{j} }}\) (Previously selected z dimension

of \(\widetilde{{x_{j} }}\)) do

6.

\(\widetilde{{x_{k}^{j} }}\) = \(\widetilde{{x_{k}^{j} }}\) + h

7.

If \(\widetilde{{x_{k}^{j} }} < x_{k}^{ \hbox{min} }\) or \(\widetilde{{x_{k}^{j} }}\rangle x_{k}^{ \hbox{max} }\) then

8.

Map \(\widetilde{{x_{k}^{j} }}\) to potential space \(\widetilde{{x_{k}^{j} }} = x_{k}^{ \hbox{min} } + \left| {\widetilde{{x_{k}^{j} }}} \right|{\% }\left( {x_{k}^{ \hbox{max} } - x_{k}^{ \hbox{min} } } \right)\)

9.

End if

10.

End for

Gaussian distribution can be used to maintain diversity in sparks generation. Gaussian expression with a standard deviation and mean of 1 i.e., \(Gaussian\text{ }\left( {\text{1,1}} \right)\) is used as shown in Algorithm 2.

Algorithm 2: For obtaining the location of a specific spark

1.

Initialize the location of the spark: \(\widehat{{x_{j} }} = x_{i}\)

2.

\(z\text{ = }round\left( {d.rand\left( {\text{0,1}} \right)} \right)\)

3.

Select \(\tilde{x}_{j}\) of z dimension randomly

4.

Calculate the coefficient of Gaussian explosion: h = A i . Gaussian (1,1)

5.

For each dimension of \(\widehat{{x_{k}^{j} }}\) (Previously selected z dimension of \(\widehat{{x_{j} }}\)) do

6.

\(\widehat{{x_{k}^{j} }} = \widehat{{x_{k}^{j} }} \cdot h\)

7.

If \(\widehat{{x_{k}^{j} }} < x_{k}^{ \hbox{min} }\) or \(\widehat{{x_{k}^{j} }} > x_{k}^{ \hbox{min} }\) then

8.

Map \(\widehat{{x_{k}^{j} }}\) to potential space \(\widehat{{x_{k}^{j} }} = x_{k}^{ \hbox{min} } + \left| {\widehat{{x_{k}^{j} }}} \right|{\% }\left( {x_{k}^{ \hbox{max} } - x_{k}^{ \hbox{min} } } \right)\)

9.

End if

10.

End for

3.1.4 Location selection

The current best location (x∗) corresponding to the lowest objective function value and the distance of other (n − 1) locations from current best location is used to select the locations for each explosion generation. Usually the two locations \(x_{i,} x_{j}\) are separated by a distance given by

$$R\text{(}x_{i} \text{)} = \sum\limits_{j \in K} {d\text{(}x_{i} ,x_{j} \text{)}} = \sum\limits_{j \in K} {\parallel x_{i} - x_{j} \parallel }$$
(25)

where K corresponds to set of current locations of fireworks and sparks. Thereupon, the probability of selection for location x i is given by

$$p\text{(}x_{i} \text{)} = \frac{{R\text{(}x_{i} \text{)}}}{{\sum\nolimits_{j \in K} {R\text{(}x_{i} \text{)}} }}$$
(26)

Algorithm 3 Heuristic adjustment

1.

Check for minimum reserve requirement

2.

If ((14) is violated) then

3.

Sort all binary 0 bit for one-time interval and Turn-On the unit according to the priority

4.

End if

5.

Check for minimum up/down time constraints

6.

If ((18) is violated) then

7.

Turn-on or turn-off units to satisfy the min. up/down time constraints along with respect to the minimum reserve constraint;

8.

End if

Algorithm 4 Heuristic adjustment

1.

Initialize all parameters of BFWA and thermal units

2.

Select random n locations with dimension G × T and calculate the objective function value

3.

for i = 1 to \(MaxItr\) do

4.

Calculate number of sparks using (21)–(22)

5.

Calculate amplitude of Explosion using (23)

6.

Obtain the location of a spark using Algorithm 1

7.

Apply pseudo-random probability transition rule for assigning unit state

8.

Carry out heuristic adjustment using Algorithm 3

9.

Calculate economic load dispatch (ELD) and fitness

10.

Obtain the location of a specific spark using Algorithm 2

11.

Apply pseudo-random probability transition rule for assigning unit state

12.

Carry out heuristic adjustment using Algorithm 3

13.

Calculate ELD and fitness

14.

For next iteration sort fitness and select based on current best location

15.

Rest of the (n − 1) locations is selected using (25)–(26)

16.

End for

3.2 Proposed BFWA for solving UCP

Before the commitment of thermal units, their ON/OFF status has to be decided. ON/OFF status of each unit is constricted by strict constraints like reserve, load satisfaction and unit’s operating characteristics like up/down times, ramp rate limits. Pertaining to such constraint satisfaction, ON/OFF status is adjusted utilizing heuristic adjustment [20]. The heuristic system shows a direct repairing strategy in constraint satisfaction through alteration of ON and OFF conditions of thermal units as indicated by their need in the event of constraint violation, while the indirect systems punish the fitness function value to avoid constraint conflict [21].

Once the ON/OFF states for thermal units are appointed, the assignment of the optimization method is to designate power generation levels of thermal units to minimize the aggregate operational cost. In this methodology firstly, the system with all BFWA and thermal unit parameters is designed. Thereupon, arbitrary locations are chosen for initiation of fireworks explosion using Algorithm 1. After that, based on Algorithm 2, the number of sparks and the amplitude of the sparks are obtained. Thereafter, (25) and (26) are used to calculate the distance of the sparks from current best spark and selection of sparks for the next generation of explosions. The explosion process is terminated when any of the termination criteria is satisfied.

4 Results and discussion

The simulations for solving UCP using BGWA are carried out in MATLAB R2012b environment operating on Mac OS X version 10.9.1 and 2.7 GHz processor. The dimensionality of the problem is considered by increasing the number of generators from 10 to 100 units and corresponding simulation results are evaluated and compared. The test system consists of 10 thermal units whose information is taken from [29] to tackle the UC problem. The generation units are committed and scheduled for a time horizon of 24 hours and for the load taken from [29]. Statistical and surveying methods being the most used ones for this purpose which estimates the availability of EV’s in parking lot for V2G deployment and inferences made from such surveys are considered in aggregating 50000 EV fleets [30]. Limit of PVG and WEC are considered to be 40 MWp and 30 MW respectively and the hourly climate information [31] on average basis is used to simulate the power generation from RETs. Model parameters for wind energy model are \(P_ \text{wtr} = \text{2100 kW}\) (14 identical turbines considered), \(V_\text{ci} ,V_\text{r} ,V_\text{co}\) are 3.5 m, 11 m, 20 m respectively and turbine parameters \(\alpha ,\beta ,\gamma\) are 23, −59, 27 respectively for 2.1 MW turbine considered. Model parameters for SPV are: \(\lambda = 0.536\;{\text{w/m}}^{ 2} \;{\text{per}}\;^\circ {\text{C}}\) [27], \(P_{mp} \text{ = 40 MW}\).

In this work, a total of five scenarios are outlined namely: ① without PEV and RET; ② with PEV for load leveling; ③ with PEV and wind energy generator (WEG); ④ with PEV and solar photovoltaic generator (SPV); ⑤ with PEV and hybrid renewable energy technology (HRET).

Case 1: Without PEV and RET

The first case comprises of the traditional electric network without RET integration and the EV deployment. The cost and emissions in this case are $579450 and 21754 tons respectively. The performance comparison and schedule for the traditional scenario is given in Table 1 and Table 2 respectively. The convergence characteristics of cost and emissions for case 1 are shown in Fig. 2.

Table 1 BFWA performance comparison for fitness value ($)
Full size table
Table 2 Load dispatch for scheduling scenario without PEV and RET
Full size table
Fig. 2
figure 2

Dual objectives convergence for case 1

Full size image

Case 2: Scheduling scenario with PEV for load levelling

In this scenario, PEV with battery or fuel cell or both of them is scheduled in conjunction with the thermal units. The PEV driving patterns and the frequency of trips information along with the network’s forecasted load is used to schedule the PEVs for load levelling application via valley filling mechanism, as shown in Fig. 3.

Fig. 3
figure 3

Load pattern with and without PEV

Full size image

In this scenario both the cost of scheduling and emissions are increased by 1.61% and 1.35% respectively when compared to the base case or the traditional case. The increase in cost and emissions can be attributed to the fact that, the charging load of PEV adds to the generation cost resulted due to increased demand and at the same time driving the generation to maximum levels thereby propelling the quadratic term of the emission function. However, the conversion of conventional fossil fuelled vehicle to green means of transportation, there is a yearly savings of 326678.766 tons [27].

Therefore, the overall equation settles down to a saving of 601 tons per day as the shift in transportation. Also, the constant hike in the oil prices and the reduction in the electricity cost adds to the benefits of the PEV deployment in terms of economic as well as environmental prospects. The convergence characteristics of cost and emissions for case 2 are shown in Fig. 4.

Fig. 4
figure 4

Dual objectives convergence for case 2

Full size image

Scheduling in smart grid

The smart grid models incorporate scheduling of RETs along with the PEV. Three possible scenarios are explored in this work as explained below.

Case 3: Scheduling scenario with PEV and SPV

In this scenario, both PEV and SPV are scheduled in conjunction with thermal units. The SPV daily generation of 306 MW per day peaking is at 13th hour, as shown in Fig. 5. The coincidence of peak solar generation and peak load resulted in offsetting of peak thermal generation units thereby reducing the cost when compared to case 1 and case 2. The reduction in cost compared to case 1 and case 2 is $ 18024.07372 and $ 23693.2972 respectively.

Fig. 5
figure 5

SPV hourly generation

Full size image

Also the emissions are reduced by 1.67% compared to case 2 as the PEV load is now supplied partly from emission-free RET (SPV). The convergence characteristics of cost and emissions for case 3 are shown in Fig. 6.

Fig. 6
figure 6

Dual objectives convergence for case 3

Full size image

Case 4: Scheduling scenario with PEV and WEG

This scenario represents PEV scheduling along with a typical wind thermal co-scheduling where, the wind generation aids the thermal power in providing the network and PEV charging load. The wind generation has a peak generation of 30 MW at 12th hour (Fig. 7) and a daily generation of 365.5 MW. The cost and emissions are reduced compared to case 1, case 2 and case 3 by $18555.47, $24224.69 and $531.40 respectively. The overall reduction in the cost compared to previous three cases is due to the higher generation from WEG compared to that from SPV. This case has also resulted in lower emissions compared to case 3 which is due increased generation from the RET (WEG). The convergence characteristics of cost and emissions for case 4 are shown in Fig. 8.

Fig. 7
figure 7

WEG hourly generation

Full size image
Fig. 8
figure 8

Dual objectives convergence for case 4

Full size image

Case 5: Scheduling scenario with PEV and HRET

This scenario presents a more advanced prospect of the smart grid i.e., incorporation of vehicle to grid (V2G) mode in scheduling scenario (Fig. 9). The convergence characteristics of cost and emissions for case 5 are shown in Fig. 10. The inherent advantage of this scenario is that, the complementary nature of WEG and SPV. The scenario has resulted in lowest cost ($ 556488) and emissions (21400.40305 tons) compared to any other scenario with PEV deployment i.e., case 2 to case 4 (Fig. 11, Fig. 12). It can be observed that, PEV charging is carried out in the off-peak hours and energy stored in battery pack of PEV is utilized at peak hours to levelize the load thereby reducing the fuel cost of the thermal units (Fig. 9). The fuel cat for different scenarios conclude that, effective use of both PEV and HRET can potentially reduce the fuel cost/generation cost for the utility (Fig. 11). The thermal unit generation scheduling for case 5 is shown in Table 3.

Fig. 9
figure 9

Charge (−ve value) and discharge (+ve value) pattern of PEV for 24 hours

Full size image
Fig. 10
figure 10

Dual objectives convergence for case 5

Full size image
Fig. 11
figure 11

Cost comparison across different scenarios

Full size image
Fig. 12
figure 12

Emission comparison across different scenarios

Full size image
Table 3 Load dispatch for scheduling scenario with PEV and HRET
Full size table

The convergence of cost and emission functions (Fig. 10) is attained at higher number of iterations compared to remaining cases which can be attributed to the increased complexity of system.

5 Conclusion

In this paper, an attempt is made to examine the impact of mediation of PEVs and RETs into power system and transportation segments as a piece of modernization of existing network into smart grid. The thermal units are then planned intelligently in conjunction with EVs and RETs accounting both economical as well as environmental viability which are often two mutually exclusive entities to deal with. Then the proposed binary version of fireworks algorithm is used to commit and schedule the thermal units along with the PEV and RET efficiently. Five scenarios are laid down of which least cost (best suited option economically) is achieved in case of thermal unit scheduling with PEVs and HRETs which could be credited to the complementary nature of SPV and WEG counterbalancing the costly plants at the peak time while minimum emissions (best suited option environmentally/sustainably) is observed in the scheduling scenario where scheduling is carried out with PEVs and HRETs. The inherent property of fast convergence of the fireworks algorithm has enabled in arriving at optimal tradeoff solution without compromising on the execution time.