1 Introduction

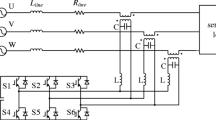
As the non-linear power load increases and the structure of distribution grid is more complex, the problems of power quality become more and more serious [1]. Especially, voltage quality problem could severely affect the normal operation of the sensitive load largely connected to the distribution grid, which leads to giant economic losses and negative effects. The complex and coupled power quality problems are commonly widespread in industries, such as automobile and electronics manufacturing, hospital and entertainment facilities [2, 3]. As the comprehensive compensation equipment of power quality, unified power quality conditioner (UPQC) is especially appropriate for solving the problems above, which can mitigate both voltage and current quality issues such as harmonic, unbalance, voltage swell and sag [4]. As shown in Fig. 1, the two converters of UPQC with the back to back combination are connected to power grid in series and shunt respectively, which makes it more suitable for voltage sag compensation with internal energy exchange [5–7].

Fig. 1
figure 1

Structure of Unified Power Quality Conditioner

Full size image

Voltage sag compensation strategy of UPQC can be divided into three types, namely pre-sag compensation, in-phase compensation, and minimum energy compensation [8–11]. The pre-sag compensation and in-phase compensation are similar to the compensation strategy of dynamic voltage restorer (DVR), which focus on minimum voltage magnitude and phase angle jump. Compare to minimum energy compensation of DVR, Ref. [12, 13] proposed a minimum VA method of UPQC (UPQC-VAmin), which utilizes non-linear optimum algorithm to calculate the injection angle of the voltage compensation so as to minimize the capacity of sag compensation. In addition, Ref. [14] proposed a voltage sag/swell compensation strategy with simultaneous active and reactive power injection by both converters of UPQC (UPQC-S), which can maximize the capacity utilization of series converter and compensate the load reactive power.

Both UPQC-VAmin and UPQC-S are based on the same principle, which determines a specific injection angle of injection voltage, for the sake of optimizing the output power of UPQC. Although these strategies can reduce the installed capacity of UPQC, they need to inject a large amount of active power, which will present difficulty in achieving sustainable compensation for voltage sag [15, 16]. However, for low voltage distribution system, on the premise of maintaining the voltage of the DC bus, UPQC usually has sufficient capability of voltage injection for voltage sag compensation. Therefore, instead of the capacity utilization, the current-carrying utilization becomes the key point of the optimized compensation strategy.

This paper proposed a simultaneous reactive power injection (UPQC-SRI) strategy for voltage sag compensation, which is based on the optimization of current-carrying utilization. This strategy uses both the series and shunt converters to inject reactive power for compensating voltage sag, and calculates the voltage injecting angle based on the minimization of current-carrying. What’s more, the zero active power injection region of UPQC-SRI (also called UPQC-SRI region) and the current limit value for the case of exceeding the UPQC-SRI region are obtained. Meanwhile, the load harmonic mitigation is also considered, and the comparison between proposed strategy and UPQC-S is also performed.

2 Principle of UPQC-SRI voltage sag compensation

The compensation phase diagram of UPQC-SRI when voltage sag occurs is shown in Fig. 2. With inductive load, for example, the series converter injects the voltage whose phase is ahead of the system. In the meantime, shunt converter injects reactive power to the system, which makes the voltage injection of series converter perpendicular to the system current. Therefore, UPQC can minimize the compensation energy and simultaneously inject reactive power by two converters. The voltage injection angle is represented as α. According to the law of cosine, the relationship of voltage vectors in Fig. 2 can be given by

Fig. 2
figure 2

Vectogram of voltage sag compensation using UPQC-SRI

Full size image
$$V_{\text{Se}}^{2} + V_{\text{S}}^{2} + 2\cos \alpha V_{\text{Se}} V_{\text{S}} = V_{\text{L}}^{2}$$
(1)

where V Se, V S and V L are the magnitude of compensation voltage, system voltage and load voltage, respectively. The compensation voltage can be derived as

$$V_{\text{Se}} = V_{\text{L}} (\sqrt {1 - D^{2} \sin^{2} \alpha } - D\cos\alpha )$$
(2)

where D is the coefficient of voltage sag, and D = V s /V L. Meanwhile, the shunt converter injects reactive power for compensating voltage sag, and the magnitude of compensation current I Sh can be given by

$$\begin{aligned} I_{\text{Sh}} &= I_{\text{L}} \left| {\cot \beta \cos\varphi - \sin\varphi } \right| = \\ &\quad I_{\text{L}} \left| {\frac{{\sqrt{1 - D^{2} \sin^{2} \alpha } }}{D\sin \alpha}\cos \varphi - \sin \varphi } \right|\end{aligned}$$
(3)

where I L represents the magnitude of load current, and φ is the power angle of load. The magnitude of system current I S is given by

$$I_{\text{S}} = \frac{{I_{\text{L}} \cos \varphi }}{D\sin \alpha }$$
(4)

Then, the current-carrying of series converter I Se is

$$I_{\text{Se}} = nI_{\text{S}}$$
(5)

where n is voltage ratio of series transformer of the UPQC.

As can be seen from (2)–(5), V Se, I S, and I Sh are the functions of voltage injection angle α, of which V Se increases with the increase of α, and I S decreases when α increases. According to (3), I Sh can be divided into two parts. The first half will increase with the increase of α, while the second part can be seen as constant. When

$$\frac{{\sqrt{1 - D^{2} } }}{D}\cos \varphi \le \sin \varphi$$
(6)

i.e. D < cosφ, I Sh increases with the increase of α. When α = 90°, the current flowing through the series and shunt converters reaches to minimum value at the same time. Then, V Se can be represented as

$$V_{\text{Se}} = V_{\text{L}} (\sqrt {1 - D^{2} } )$$
(7)

The current of shunt converter I Sh is given by

$$I_{\text{Sh}} = I_{\text{L}} \left( {\frac{{\sqrt {1 - D^{2} } }}{D}\cos\varphi - \sin\varphi } \right)$$
(8)

The current which flows through series converter is

$$I_{\text{Se}} = \frac{{nI_{\text{L}} \cos \varphi }}{D}$$
(9)

On the contrary, when D > cosφ, the current magnitude of the shunt converter can be zero by adjusting voltage injection angle α of the series converter. In this case,

$$\alpha = \arcsin \left( {\frac{\cos \varphi }{D}} \right)$$
(10)

This conclusion is consistent with the minimum energy compensation in [9].

The above conclusions are also suitable for the case of capacitive load. Under the consideration of different circumstances of voltage sag, α can be determined as 90° using the compensation strategy of USQC-SRI. The phase diagram is shown in Fig. 3. This method can realize zero active power injection of voltage sag compensation with minimized converter current-carrying, and can compensate the load reactive power. However, the aforementioned conclusions are deduced under an ideal condition without considering current limitation. So UPQC-SRI strategy with the constraint of current-carrying limit will be discussed in the following sections.

Fig. 3
figure 3

Vectogram of voltage sag compensation using minimum current method with zero active power injection

Full size image

3 Analysis of zero active power injection region using UPQC-SRI

3.1 Analysis of current-carrying requirements

Several researches mainly focus on capacity optimization of the UPQC [13–16]. However, the proposed strategy focuses on the limitation of current-carrying capability due to the following reasons.

  1. 1)

    Generally, UPQCs are directly installed at the non-linear and sensitive load at low voltage level. Taking 380 V three-phase system as an example, UPQC consists of three groups of single-phase full-bridge back to back converters using IGBTs as switches, as shown in Fig. 1. The DC bus voltage could exceed 600 V.

  2. 2)

    Using the proposed strategy, UPQC could maintain the voltage of dc bus without the output of active power (assuming the loss of UPQC could be ignored). Therefore, the series converter can operate in any circumstances of voltage sag without the limitation of the compensation voltage by properly designing the ratio of the series transformer.

  3. 3)

    The system current is the vectorial sum of the load current and the shunt converter compensation current. When severe voltage sag occurs, the magnitude of the system current will be larger than the load current, which could lead to the overcurrent of converters using UPQC-SRI. Based on (8) and (9), the current-carrying capability of UPQC has close relationship with the condition of the voltage sag and the voltage ratio of the series transformer.

As a result, current-carrying capabilities of both converters become the main factors of the voltage compensation. Specially, in section 3.1 to 3.3, the load harmonic mitigation is ignored, which will be elaborated in section 3.4. The current-carrying curves can be plotted as Figs. 4 and 5 based on (8) and (9).

Fig. 4
figure 4

Curves of I Sh using UPQC-SRI under different voltage sag conditions

Full size image
Fig. 5
figure 5

Curves of I S using UPQC-SRI under different voltage sag conditions

Full size image

Assume I L equals to 1 p.u. and the ratio of the series transformer is 1:1. As shown in Figs. 4 and 5, when D = cosφ, I Sh achieves zero, and I S equals to I L. When D > cosφ, I S will be smaller than I L because reactive current is injected from shunt converter with the opposite phase to the reactive component of load current during the voltage compensation using UPQC-SRI. When D < cosφ, although UPQC-SRI could compensate the voltage sag by reactive power injection, the shunt converter will inject reactive current with the same phase as the reactive component of load current. Then, the magnitude of system current will become larger than the load current. As the result, I S is likely greater than I L using UPQC-SRI, which would cause the overcurrent of UPQC.

With consideration of the cost of UPQC, the two converters have the same insulation level, current-carrying ability and capacity. In consequence, it is necessary to properly design the transformer voltage ratio to enlarge the UPQC-SRI region.

3.2 UPQC-SRI region and current limit

The voltage ratio of the UPQC series transformer has close relationship with UPQC-SRI region. If there is no limitation of the voltage injection magnitude, then the constraint of the series coupled transformer voltage ratio is

$$n < \frac{{V_{\text{L}} \sqrt {1 - D^{2} } }}{{m_{\text{c}} V_{\text{DC}} }}$$
(11)

where m c is the modulation ratio and V DC is the DC bus voltage of UPQC. Assume V DC = 600 V with the consideration of cost and insulation, D = 0, m c = 0.85, and n < 0.61 under the circumstance of severe voltage sag. The voltage ratio of the transformer can be set to 3:5, and the following discussion will be based on these settings of the parameters.

Let m i denote the current-carrying ratio of series and shunt converter,

$$m_{\text{i}} = \frac{{I_{\text{Sh}} }}{{I_{\text{Se}} }} = \frac{{\sqrt {1 - D^{2} } \cos \varphi - D\sqrt {1 - \cos^{2} \varphi } }}{n\cos \varphi }$$
(12)

Assume that the current-carrying capacity of UPQC equals to the rated load current magnitude, and then UPQC-SRI region can be obtained as Fig. 6 based on (8), (9) and (12).

Fig. 6
figure 6

Contour map of UPQC-SRI region

Full size image

The cases when I Se = I L = 1 p.u. and I* =I Sh = I L = 1 p.u. are illustrated in Fig. 6 in black and red lines, where I* is the current capacity of UPQC. The contour curves of m i at n = 0.6 are displayed. As can be known from Fig. 6, the area without shadow is UPQC-SRI region, which could compensate the voltage sag with simultaneous reactive power injection of both converters. When the voltage sag occurs in the shadow area, it will cause overcurrent using UPQC-SRI. According to the current magnitude of two converters and the overcurrent conditions, the shadow area could be divided into four regions(Region I, II, III and IV).

  1. 1)

    Region I: When the voltage sag happens in this area, the current-carrying of the series converter will be larger than the shunt converter, and the overcurrent will occur at the series converter. In order to avoid the overcurrent of the series converter, I Sh needs to be limited, which can be represented by I Sh_limit

    $$I_{{{{{\rm Sh}\_{\rm limit}}}}} = \left| {\sqrt {\left( {\frac{{I^{\ast} }}{n}} \right)^{2} - \,(I_{\text{L}} \cos \varphi )^{2} } - I_{\text{L}} \sin \varphi } \right|$$
    (13)
  2. 2)

    Region II: When the voltage sag occurs in this area, both the series and shunt converters would exceed their current limits using UPQC-SRI, and then the current of shunt converter needs to be clamped. The amplitude of current limit is I Sh_limit.

  3. 3)

    Region III: In this area, the current-carrying of series converter will be smaller than the shunt converter. Only the current of shunt converter will exceed its limit. Then the current limitation of shunt converter should be I*.

  4. 4)

    Region IV: In this area, the current-carrying of series converter will be smaller than the shunt converter. Both converters will exceed their current limit, and I* should also be the limit of shunt converter.

As the result, compared with the conclusion (namely D > cosφ) of [9], UPQC-SRI can obtain a larger region of zero active power injection with proper design of n.

3.3 Comparative analysis of active power injection

The clamping current of shunt converter is required using UPQC-SRI strategy. When the shunt current reaches its limit, the phase diagram of voltage compensation is shown in Fig. 7. Due to the current limit, the system current will be no longer perpendicular to the injected voltage of series converter, and the angle is γ. It implies that series converter injects active power P inj to the load, where

Fig. 7
figure 7

Vectogram of voltage sag compensation simultaneously considering the current-carrying limit of UPQC

Full size image
$$\begin{aligned} P_{\text{inj}} &= \overrightarrow {{V_{\text{Se}} }} \cdot \overrightarrow {{I_{\text{S}} }} = V_{\text{Se}} I_{\text{S}} \cos \gamma = \\ &\quad V_{\text{L}} \sqrt {1 - D^{2} } (I_{\text{L}} \cos \varphi - \textit{DI}_{{{{{\rm Sh}\_{\rm limit}}}}})\end{aligned}$$
(14)

According to (14), the more severe voltage sag occurs, the more active power is required from UPQC.

Compared with [14], the demand of active power injection using UPQC-S strategy P inj` can be given by

$$P_{\text{inj}}^{\prime} = V_{\text{L}} I_{\text{L}} \left[ {\cos(\varphi - \delta_{\hbox{max} } ) + \frac{{\cos \delta_{\hbox{max} } }}{D}} \right]$$
(15)

where δ max is the maximum difference value of phase angle between the pre-compensated and compensated load voltage. Assuming the voltage limit of V Se for UPQC-S and UPQC-SRI is the same, then cosδ max = 0.5 can be obtained. When the voltage sag occurs in region III or region IV, the active power injection ratio of UPQC-SRI to UPQC-S is defined as m p, which can be given by

$$m_{\text{p}} = \frac{{P_{\text{inj}} }}{{P_{\text{inj}}^{\prime}}} = \frac{{\sqrt {1 - D^{2} } (\cos \varphi - D)}}{{\cos(\varphi - \delta_{\hbox{max} } ) + \frac{{\cos \delta_{\hbox{max} } }}{D}}}$$
(16)

According to (16), the ratio of output active power is shown in Fig. 8 with contour curve of m p. When the sag happens in the shadow area, zero active power will be injected for the voltage sag compensation using UPQC-SRI. When the severe sag occurs, the demand for active power injection using UPQC-SRI is also smaller than that one using UPQC-S. Therefore, UPQC-SRI can provide more sustaining compensation for the voltage sag.

Fig. 8
figure 8

Active power injection comparison of UPQC-S and UPQC-SRI during voltage sag

Full size image

3.4 Consideration of harmonic mitigation

As the comprehensive compensation equipment, UPQC is able to mitigate both current and voltage power quality issues. However, there may be a conflict when mitigating voltage sag and load harmonic current at same time using UPQC-SRI, which will narrow down the UPQC-SRI region or cause the overcurrent of shunt converter. Therefore, it becomes much more complicated to deal with these two power quality issues at same time. Generally, the comprehensive mitigation of voltage sag and load harmonic current could be divided into three conditions.

  1. 1)

    Condition I: When the voltage sag occurs in UPQC-SRI region, the mitigation of voltage sag and load harmonic current can be performed at the same time. The overcurrent will only happen in shunt converter if the harmonic component of load current is very large. Therefore, the current limit of shunt converter can be represented as I*.

  2. 2)

    Condition II: When the voltage sag occurs in region I or II, the current-carrying of series converter will become larger than that of shunt converter. Thus, the shunt converter may have extra current capacity for the mitigation of load harmonic current using UPQC-SRI. Under this condition, the current injection of shunt converter should be limited. Different from Condition I, the fundamental component of shunt current should also be clamped at a proper value, which can avoid the overcurrent of both series and shunt converters. It can be given by

    $$\left\{ \begin{aligned} I_{{{\text{Sh}}\_\text{limit} \_{\text{f}}}}& = \left| {\sqrt {\left( {\frac{{I^{\ast} }}{n}} \right)^{2} - (I_{\text{L}} \cos \varphi )^{2} } - I_{\text{L}} \sin \varphi } \right| \hfill \\ \!I_{{{\rm Sh}\_\text{limit} }} &= I^{\ast} \hfill \\ \end{aligned} \right.$$
    (17)

    where I Sh_limit_f is the clamped value of fundamental component of shunt current.

  3. 3)

    Condition III: When the voltage sag condition occurs in region III or IV, the current-carrying of series converter will be smaller than that of shunt converter, and the current limit of the shunt converter is represented as I*. Thus, the shunt converter may not have extra current capacity for mitigation of load harmonic current. Therefore, under this condition, the mitigation of load harmonic current should turn off during the voltage sag period.

4 UPQC-SRI algorithm and its validation

4.1 Compensation algorithm

The block diagram of the closed-loop control algorithm is shown in Fig. 9.

Fig. 9
figure 9

Per-phase control block diagram of voltage sag simultaneously compensation

Full size image

For the closed-loop control of series converter, the vector of system voltage is constructed in αβ coordinate using delay operation [17]. Then the system voltage can be transformed into dq coordinate. After that, the system voltage will be transformed to DC component on d axis. Then, D can be calculated in real-time property [18]. Since the compensation voltage is perpendicular to the system voltage, the transformed compensation voltage only exists in q axis. Based on above calculation, the modulation voltage is obtained, which needs to be transformed to the abc coordinate. The difference between referenced compensation voltage and output compensation voltage caused by series transformer needs to be adjusted using proportion resonance (PR) controller. The resonant frequency of PR controller is set at 50 Hz in this paper [19].

For the shunt converter, the same transformation is used to calculate the shunt current. The elements of I Lcosφ and I Lsinφ in (8) are transformed to the DC components in d and q axis, respectively. As a result, load power factor could be measured in real-time property. Therefore, the detection delay of load switching can be determined by the design of digital filter. Furthermore, the pulse width modulation can be generated by classical dual closed-loop control. In order to achieve the stationary charge-discharge of DC capacitance, a ramp function is used in DC bus voltage control. Specially, a saturate block in the q axis is demanded due to the current-carrying limit. DC voltage control should be stopped during voltage sag period. And then the UPQC will not absorb active power, which may cause more severe voltage sag.

4.2 Simulation results

In order to verify the validity of UPQC-SRI, a PSCAD/EMTDC simulation model is constructed. The parameters of simulation are shown in Table 1.

Table 1 Parameters of the simulation systems
Full size table

In this simulation, voltage sag occurs at 1.5 s with D = 0.6, and the duration is 150 ms. The current limit of the UPQC is set at 18 A (peak). The proposed strategy is tested under two load conditions, which are in and out of the UPQC-SRI region, respectively.

4.2.1 Condition 1

The root mean square (RMS) value of load phase current is 14 A, and the power factor is 0.74. The theoretic output current of the shunt converter is 4.4 A, which is smaller than the limitation 9.07 A according to (8) and (12). Therefore, this voltage sag occurs in the UPQC-SRI region, and the waveform is shown in Fig. 10.

Fig. 10
figure 10

Simulation results of UPQC-SRI under condition 1

Full size image

As shown in Fig. 10, before the voltage sag happens, injection voltage of series converter equals to zero and the shunt converter provides reactive power compensation for the system. The voltage recovers to the normal rating within half cycle after voltage sag occurs. The angle of voltage injection of the series converter is 90 degrees ahead of system voltage due to the inductive load. Meanwhile, the shunt converter injects inductive reactive power so as to make the system current perpendicular to injection voltage. Then, the system voltage is in phase with system current. Because there is no active power exchange, the DC bus voltage of UPQC drops a little. After sag period, the DC voltage returns to the rating under the control of DC voltage.

4.2.2 Condition 2

In this condition, load phase current is 16 A (RMS) and power factor is 0.96. According to (8), the theoretic minimum value of zero active power injection current of the shunt converter is about 16 A (RMS), which will lead to the overload of the series converter.

This condition of voltage sag exceeds the UPQC-SRI region, and the waveform is shown in Fig. 11. According to Fig. 6, the voltage sag condition occurs in region I, in which the series converter overload may happen. According to (13), the limit current of shunt converter is 10.15 A (peak). Due to the active power injection, the DC bus voltage no longer sustains. After the voltage sag period, the dc bus voltage returns to normal rating gradually.

Fig. 11
figure 11

Simulation results of UPQC-SRI under condition 2

Full size image

4.2.3 Transient response and algorithm comparison

In order to ensure the real-time property of corresponding control algorithm, the PR controller is utilized to track the sinusoidal reference voltage. Meanwhile, the real-time sampling of power factor is performed. The simulation result is represented in Fig. 12.

Fig. 12
figure 12

Dynamic simulation results of UPQC-SRI

Full size image

The simulation starts from condition 1, and the transient of the load switching occurs at 1.6 s. Then, the load condition switches to condition 2. The result indicates that the PR controller can accurately and quickly track the reference voltage, and the transient response of shunt current t d is shorter than 10 ms.

As can be seen from Fig. 13, the voltage of DC bus drops more deeply using UPQC-S, which means the more active power injection than UPQC-SRI during voltage sag. Therefore, the analysis in section 3.3 can be verified by the simulation results. Compared with UPQC-S, the proposed strategy can provide more sustainable voltage sag compensation.

Fig. 13
figure 13

Simulation comparison between UPQC-S and UPQC-SRI

Full size image

5 Conclusion

Firstly, the principle of voltage sag compensation is derived in this paper. And then UPQC-SRI voltage compensation strategy with optimal configuration of current-carrying is proposed. This strategy can achieve the control of unity power factor and provide sustainable voltage sag compensation by simultaneous reactive power injection from both shunt and series converters of the UPQC.

With consideration of current-carrying limit, the UPQC-SRI region is presented, and then the limit value of the shunt current is obtained. Furthermore, the conditions for compensating both the voltage sag and the load harmonic current are analyzed under three sag conditions.

Finally, the UPQC-SRI strategy and the corresponding algorithm are verified by PSCAD/EMTDC platform. Both the analysis and the simulation results indicate that when the severe voltage sag occurs, UPQC-SRI can compensate the voltage sag with less active power injection than using the traditional strategies.