Wind farm polymerization influences on security and economic operation in power system based on Copula function

Abstract

Wind speed dependences on different areas in a wind farm have influences on security and economic operation in power system. In order to simulate the correlation of wind speed series between different positions, this paper applies Copula function and rank correlation matrix methods to measure the coherence of wind speed in a wind farm. The correlated wind sample space is established. According to active power output characteristics of wind turbines, the polymerization model in a wind farm can be achieved. Monte Carlo optimal power flow is applied to IEEE-30 and IEEE-300 bus systems based on the principle of energy saving dispatching. The study shows that the accuracy of outputs is improved, thus reducing the fluctuation ranges in unit generating costs and power flow in branches while considering wind speed polymerization. This approach provides a new method to improve the effectiveness of energy saving dispatching and system operation arrangement. Results have been tested to be effective.

1 Introduction

Wind energy is a kind of green and clean energy which plays an important role in optimizing modern energy structure. Developing wind energy will be of benefit to reduce fossil energy consumption and carbon emissions. But as wind power is applied to the power system, the wind abundance is becoming more and more serious. How to economically and safely use wind energy is a new challenge in the globe [1]. To solve the power system operation problems containing the sustainable energy, the principle of energy saving dispatching has been introduced. It means before using the clean energy, we should firstly consider unit consumptions and pollution emission to make generation scheduling. Based on this principle, accurately forecasting wind speed can improve wind power consumption and the energy saving dispatching.

The current wind speed forecasting model can be classified into physical model and historical wind model. The former is used to forecast wind speed based on numerical weather report while the latter uses historical wind speed to extrapolate. Wind resource has certain regional feature which means different positions has varies values in a wind farm. But at present researches always assume that wind speed of every wind turbines in a wind farm is equal [2–4] at the same time when studying wind model we often assume. Apparently, these models cannot accurately reflect the wind speed in reality [5, 6]. Therefore, it will affect wind farm outputs because lack of wind speed correlation and further influence power dispatching and power system operation. In order to improve the capability of energy-saving power generation dispatching and wind power consumption, studying the influence of correlative wind of large wind farm is essential and wind speed polymerized model should be introduced.

In conventional studies, there are mainly three methods to analyze wind speed correlation: 1) establishing wind speed correlation sequences based on autoregressive moving average (ARMA) model [7]; 2) orthogonal transformation method based on the Cholesky decomposition to linear correlation coefficient matrix of wind speed [8, 9]; 3) Nataf transform method considering the relationship between linear correlation matrixes of wind speed and standard normal distributions [10, 11]. These three methods all assume that the correlative wind speed sequences can meet the same distribution. However, the wind speed in a farm can subject to different distributions because of different locations. Copula function based on correlation measurement can solve the problem very well. Since Copulas have been applied to financial problems [12, 13], in power system, they are proved to be effective. Zhang [14] used Copula functions to establish the dependency probabilistic sequence theory and used the arithmetic to analyze total output probability distribution of multiple wind farms. Copula functions are adopted to establish the correlation of wind speed in multiple wind farms and the dependency of load demand [15–17]. In [18–20], mixed Copula functions are analyzed when the dependence between wind speed series is studied. But they did not give the reason why choose some Copula functions as the basis of mixed function, at the same time, whether it is a good choice to estimate the weight of each Copula function in mixed model is still questionable.

This paper proposes a modeling method based on Copula functions to deal with the wind speed distribution characteristics and their correlation features. That is, getting the Copula function parameters through cumulative probability distribution function of historical wind speed; based on the rank correlation theory, selecting suitable Copula functions to simulate wind speed sample; and then achieving wind power output model of which containing wind speed dependence. Using the model in IEEE-30 and IEEE-300 bus systems for Monte Carlo optimal power flow calculation whose objective function is the minimum power consumption to analyze the influences on wind farm polymerization model in power system.

2 Wind farm polymerization model based on Copula function

2.1 Copula function and basic concepts

Sklar theorem presents an n-dimension function which can be decomposed into n number marginal distribution functions and a Copula function. In Copula function, it describes the correlation of each marginal distribution variable and connects random variables’ marginal distributions [21].

Functions $F_{{X_{1} }} (x_{1} ),\;F_{{X_{2} }} (x_{2} ), \cdots ,\;F_{{X_{n} }} (x_{n} )$ can be decomposed into $C(u_{1} ,\;u_{2} , \cdots ,u_{n} )$:

$$F(x_{1} ,\;x_{2} , \cdots ,x_{n} ) = C[F_{{X_{1} }} (x_{1} ),\;F_{{X_{2} }} (x_{2} ), \cdots ,F_{{X_{n} }} (x_{n} )]$$

(1)

If random vectors $U_{1} ,U_{2} , \cdots ,U_{n}$ follows a uniform distribution on the interval [0, 1], the marginal distribution functions $F_{{X_{1} }} (x_{1} ),\;F_{{X_{2} }} (x_{2} ), \cdots ,F_{{X_{n} }} (x_{n} )$ of random vectors $X_{1} ,\;X_{2} , \cdots ,X_{n}$ can be described [15, 16] as:

$$F_{{X_{i} }} (x_{i} ) = u_{i} \quad i = 1,2, \cdots ,n$$

(2)

where $u_{i}$ is the element of vector $U_{i}$.

The equal probability inverse transformation random variables can be achieved as:

$$x_{i} = F_{{X_{i} }}^{ - 1} (u_{i} )\quad i = 1,2, \cdots ,n$$

(3)

Then (1) can be written as:

$$C[u_{1} ,\;u_{2} , \cdots ,u_{n} ] = F[F_{{X_{1} }}^{ - 1} (u_{1} ),\;F_{{X_{2} }}^{ - 1} (u_{2} ), \cdots ,F_{{X_{n} }}^{ - 1} (u_{n} )]$$

(4)

2.2 Spearman rank correlation

There are many kinds of methods to measure correlation of variables. Linear correlation is one of common indicators:

$$\rho_{{R_{L} }} = \frac{{\text{cov}} {(X_{1} ,X_{2} )}}{{\sqrt {\text{var}} {(X_{1} )} \sqrt {\text{var}} {(X_{2} )} }}$$

(5)

where $\rho_{{R_{L} }}$ is the linear correlation between random variable $X_{1} ,X_{2}$; $\text{cov} ( \cdot )$ is the covariance; $\text{var} ( \cdot )$ is variance.

Linear correlation only reflects the linear correlation among random variables. The linear correlation does not change when random variables make the same linear transformation. But if the transformation is nonlinear, linear correlation will change. In order to avoid the correlation deviation when wind speed deals with nonlinear transformation, higher correlation study should be introduced. This paper, introduces Kendall and Spearman rank correlation to test the dependence of wind speed.

Assuming that random variables $(x_{i} ,y_{i} )$ $(x_{j} ,y_{j} )$ are separated and identically distributed with vector $\text{(}X,\;Y\text{)}$, Correlation coefficient of Kendall $\tau$ and correlation coefficient of Spearman $\rho_{s}$ can be defined as:

$$\tau = \frac{2}{n(n - 1)}\sum\limits_{i = 1}^{n} {\sum\limits_{i < j} {\text{sgn} [(x_{i} - x_{j} )(y_{i} - y_{j} )]} }$$

(6)

$$\rho_{s} = \frac{{\sum\limits_{i = 1}^{n} {(x_{i} - \overline{x})(y_{i} - \overline{y})} }}{{\sqrt {\sum\limits_{i = 1}^{n} {(x_{i} - \overline{x})^{2} } } \sqrt {\sum\limits_{i = 1}^{n} {(y_{i} - \overline{y})^{2} } } }}$$

(7)

where $\overline{x} = \frac{1}{n}\sum\limits_{i = 1}^{n} {x_{i} }$; $\overline{y} = \frac{1}{n}\sum\limits_{i = 1}^{n} {y_{i} }$.

It can be found during the same monotony when making nonlinear transformation, coefficients $\tau$ and $\rho_{s}$ would not change [15].

3 Wind speed modeling based on Copula function and its rank correlation

3.1 Modeling process of correlative wind speed

According to the measuring wind speed in history of a mountainous wind farm in Yunnan, China. This paper uses Copula function to establish the correlative wind speed model. The total installed capacity of wind farm is 198 MW. Its unit capacity is 1.5 MW. Wind turbines are distributed in 6 different mountains whose height varies from 1800 to 2510 m. These 6 mountain areas are 19.3, 14.2, 11.2, 20.0, 21.2 and 18.6 square km. History data (16,086 × 6 number) are measured: wind speeds are from January 2011 to December 2011 in a day of every midmonth in a year. Measurement step is 1 min.

Figure 1 shows the Spearman rank correlation matrix of historical wind speed sample. The sample consists of 6 wind speed sequences of mountains, therefore, Spearman rank correlation matrix is a matrix of 6 × 6. From the Fig. 1, we can find that each wind speed sequence in a farm is dependent with other sequences.

Fig. 1

Wind speed rank correlation

3.1.1 Weibull estimate marginal distribution of wind sample

In current research, many parametric distributions have been used to model wind speeds, such as Rayleigh, $\chi^{2}$ and ECDF distributions. In this paper Weibull distribution is supposed to estimate wind speed series parameters. Weibull distribution is perfect to model curve shape of wind speed series and its accuracy has been verified [22–24].

Weibull function is described in (8), through moment estimation method we can get group parameters of 6 mountains’ wind speed samples.

$$f(v_{w} ,c_{w} ,k_{w} ) = \frac{{k_{w} }}{{c_{w}^{k} }}v_{w}^{k - 1} {\text{e}}^{{ - (\frac{{v_{w} }}{{c_{w} }})^{{k_{w} }} }}$$

(8)

where $v_{w}$ is wind speed; $c_{w}$ and $k_{w}$ are separately scale and shape parameter; $c_{w}$ reflects the annual average wind speed.

Parameters in Table 1 are the foundations of solving probability distribution of each wind sequence.

Table 1 Weibull distribution parameters of a mountain

3.1.2 Copulas for modeling wind speed correlation

Appendix A lists the probability density function of each Copula function. We can obtain parameters of wind speed sample each Copula function by using parameter estimation method. To simplify the description, the dependence of wind speed in mountain 1^th and mountain 2^th is discussed in this paper (similar to other wind speed). For each Copula model, the 16086 groups of data are generated. Table 2 shows estimated parameters of each Copula of historical samples.

Table 2 Copula parameters of historical samples

Using obtained parameters, through inverse Weibull transformation, the wind speeds v ₁ ,v ₂ containing Copula correlation are generated. By P–P test, wind speed series generated by the function models are approximately coincident with actual wind sample (Appendix B), which indicates that Copula function modeling wind speed is reasonable [14]. In order to distinguish the results of different functions, probability density map of each wind model is proposed, and their rank correlation levels are also referred to measure the accuracy of each model. Finally, empirical Copula function is introduced to study the distance between wind sample and data points in Copula model.

Figure 2 shows the probability density function of wind sample and Copula models.

Fig. 2

Probability density function of each model

From Fig. 2, it is easy to find that Gumbel Copula is lost correlation information in bottom tail and top tail of Clayton Copula. However, original sample is a symmetrical distribution, which means Gumbel Copula and Clayton Copula are unsuitable. Fig. 2b is coincident with Fig. 2a, modeling original wind speed by Gaussian Copula function is correct. T-Copula is good to model the original data, but the distribution has a sharp tail in both top and bottom while actual wind speeds in fast and slow have considerable probability. Frank Copula is used to describe original data, but is not better than t-Copula nor Gaussian Copula.

Table 3 lists rank correlation of generated series in each Copula model. From the table, Frank Copula has a better performance than any other Copula function in Kendall; and in Spearman, rank correlation of Gaussian Copula model is the closest to the original values.

Table 3 Rank correlation of generated series

In order to quantify this evaluation, the empirical Copula function is introduced to test their correctness.

$(x_{i} ,y_{i} )$ (i = 1,2,…,n) is the sample of (X,Y), and F _n (x), F _n (y) are separately empirical distributions of variable X and Y, empirical Copula function can be describe as:

$$\hat{C}_{n} (u,v) = \frac{1}{n}\sum\limits_{i = 1}^{n} {I_{{[F_{n} (x_{i} ) \le u]}} } I_{{[F_{n} (y_{i} ) \le v]}} \;\;\;u,v \in [0,1]$$

(9)

And the evaluation equals to the distance between wind speed points generated by Copula function and empirical Copula function:

$$d_{C}^{2} = \sum\limits_{i = 1}^{n} {\left| {\hat{C}_{n} (u_{i} ,v_{i} ) - \hat{C}(u_{i} ,v_{i} )} \right|}^{2}$$

(10)

Total distances of all points in each Copula function model are shown in Table 4.

Table 4 Distances of Copula model to empirical Copula

In Table 4, Gaussian Copula has the shortest distance compared with other functions. Thus, Gaussian Copula is the best choice to this model.

3.1.3 Copula function assessment

For Copula models, although we have verified that Gaussian Copula has a better performance than other Copula function in this sample. There is still needed to test its fitting property with original sample. Hence, Diehoid financial principle ‘Assessment of density distribution model based on series probability integral transformation’ is introduced [25, 26]. In this principle, the general idea of Diehoid is: obtaining a new series from the original data by probability integral transformation, and then testing whether the new series is independent and identically distributed to (0, 1) uniform distribution. In this paper, it is divided as two steps: (1) Transforming the Copula wind model under the Weibull distribution by probability integral transformation, and then testing the autocorrelation of each transformed series probability to see whether series itself independent; (2) Using Kolmogorov-Smirnov (K-S) principle to check transformed series keeps (0, 1) uniform distribution. We could recognize that the marginal distribution of wind speed sample by Copula modeling is correct.

The marginal bound of autocorrelation from Copula models is [−0.0158, 0.0158], which means each wind speed series is none autocorrelation. The results of K-S test are shown in Table 5.

Table 5 Results of K-S test

The statistical values show that for six series we have no reasonable excuse to reject null hypothesis, that is “transformed series obey [0, 1] uniform transformation”. Results show that Gaussian Copula is excellent to model the marginal function of each speed series, and it is reasonable.

3.2 Wind farm output polymerization model

How to formulate the Gaussian Copula model from original sample from Weibull estimated is shown in Fig. 3.

Fig. 3

Gaussian Copula transformation procession

The output quality of wind turbines can be described as:

$$P_{w} = \left\{ \begin{aligned} &0 \qquad\qquad\qquad v < v_{{wi}} ,v\; > \;v_{{wo}} \hfill \\ &\frac{{v^{n} - v_{{wi}}^{n} }}{{v_{r}^{n} - v_{{wi}}^{n} }}P_{r} \,\,\qquad v_{{wi}} \le v < v_{r} \hfill \\ &P_{r} \,\,\,\quad\qquad\qquad v_{r} \le v \le v_{{wo}} \hfill \\ \end{aligned} \right.$$

(11)

where v _wi , v _wo is cut-in speed and cut-out speeds. In this paper, we suppose their values are 4 and 25 m/s. v _r is rated wind speed about 15 m/s. P _r is wind turbine rated output, in this paper, it is 1.5 MW; $n$ is wind-power coefficient, taking 3 usually.

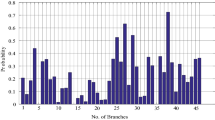
Taking the wind speed model by Gaussian Copula function into (11), the polymerization model of wind farm has accomplished. Figure 4 shows the frequency of polymerization model about wind farm output whose sample is 16086.

Fig. 4

Frequency of polymerization model in wind farm output

4 Optimal power flow calculation when containing wind farm

When calculating optimal power flow (OPF) whose objective function is minimum power generation cost, the wind turbine can be connected to power system as negative load [27]. This model can be applied to energy-saving power generation dispatching scheme. In this model, the consumption level of generator unit is reflected by generator consumption characteristics. Wind turbines connecting to power system as a negative load will conform to the requirements of energy-saving power generation dispatching. Under the guarantee of reliable power supply, the scheme requires dispatching renewable resource prior and then scheduling fossil power generation resources successively according to the generating unit energy consumptions and pollutant emission levels from low to high orders.

This paper calculates OPF of power system which contains thermal generation and wind farm generation. Due to the priority scheduling for wind power, the wind farm connects to a system as a negative load and is treated as PQ bus in power flow calculation. With the minimum power generation cost objective function, power balance equations and system safe operation constraints, OPF can make the priority scheduling of renewable power generation resources and the lowest levels for energy consumption goal come true (Appendix C and Appendix D) [28].

5 Calculation process

The calculation process can be divided into four parts. The first part is rank correlation matrix and Weibull distribution parameters of history record wind speeds. Secondly, it models correlative wind speeds in different hills of a mountainous wind farm based on Multivariate Gaussian Copula function. The wind farm polymerization model is obtained according to output characteristics of wind turbines Thirdly, Monte Carlo optimal power flow is taken. That means in different outputs of a wind farm, the basic power flow and optimal power flow are calculated to obtain the unit generating cost of the system (thermal power generation cost/total thermal power generating capacity) as well as branch power flow. Finally, we use a probability statistics method to the unit generating cost and branch power flow. The calculation process is shown in Fig. 5.

Fig. 5

Calculation process

6 Case studies

The mountainous wind farm polymerization model is connected to IEEE-30 and IEEE-300 bus systems [29]. This paper calculates optimal power flow under the principle of energy-saving power generation dispatching in order to inspect the mean values and standard deviation of branch power flow, as well as the probability density and cumulative probability distribution of unit generating cost.

6.1 IEEE-30 bus case

There are 30 buses including 6 generator buses, 41 branches including 37 line branches and 4 transformer branches in IEEE-30 bus system. The mountainous wind farm is connected to a heavy load bus without power supply. This paper establishes a polymerized model based on multivariate Gaussian Copula function. The impacts of wind farm polymerization are analyzed by taking 16086 Monte Carlo optimal power flow calculations.

Parts of branch power flows’ expectation and standard deviation are shown in Table 6. Table 6 consists 3 group results of 3 different models: 1) polymerization model; 2) without polymerization model considering Weibull distributions to model the wind speed; original wind speed samples (data of historical wind speed). It can be seen, compared with results of un-polymerization model the results of polymerization model based on Copula function are closer to those of historical wind speed. The model considering wind speed dependence makes the results of each Monte Carlo calculation more focused on, as shown in Table 6 Total branch deviations of polymerization are smaller than those of without polymerization model.

Table 6 Mean values and standard deviation of part branch power flow

Table 7 gives the total deviations of the branch power of IEEE-30 bus system. The polymerization has a smaller deviation. The actual significance is that after considering wind dependence, decreasing numbers of Monte Carlo optimal power flow calculations will not influence the accuracy of results. Usually, an optimal power flow calculation of a large system requires considerable computation time; for the system incorporating wind power, since the fluctuation of wind speed, it is necessary to increase the number of calculation to insure the accuracy of results. Therefore, it comes to taking large time in Monte Carlo optimal power flow computation. Copula function can conquer this shortcoming, the wind speed model considering dependence makes wind turbine model output more concentrated which will cut off the calculating time and insure the precision at the same time. In all, the Copula model is useful for energy-saving power generation dispatching strategy as well as system operation mode arrangement.

Table 7 Total deviations of branch power in system

Figure 6 shows the cumulative distribution function (CDF) curves of branches 5-7 power. And Fig. 7 shows the density distribution function of that branch power. From the curves, it is easy to find the bus 7^th which has wind power to be incorporated, polymerization model fits better than without polymerization model in the probability.

Fig. 6

Cumulative probability distribution of power branches 5–7

Fig. 7

Probability density distribution of power branches 5–7

Figure 8 shows the mean values of locational marginal price (LMP) of IEEE-30 system after Monte Carlo calculations. We can find that results of polymerization model are very close to those of historical samples which emphasizes verification of Copula function.

Fig. 8

Locational marginal price in IEEE-30

6.2 IEEE-300 bus case

IEEE-300 bus case is based on software matpower4.1 to run 1000 Monte Carlo calculations. There are 300 buses including 69 generator buses, 411 branches in IEEE-300 bus system. The base capacity is 100 MW. The mountainous wind farm is connected to Bus 20. Results show that the similarity of which comes out of IEEE-30 bus.

Figure 9 is the result based on system IEEE-300 which shows the accuracy of the proposed method. Total power flow of 411 mean values of branches of polymerization model is 51843.53. It is very close to the original model’s result. The difference between them is only 15.53 which means the little distinction can be ignored. Figure 10 is the comparison of CDF of marginal generating cost between two models which shows that polymerization model fit the original data.

Fig. 9

Locational marginal price in IEEE-300

Fig. 10

CDF of marginal generating cost

7 Conclusion

The research shows that the fluctuation of generator output and branch power flow are smaller when considering wind farm polymerization effects. And the result also shows that compared with normal wind speed model, the polymerization has a better property to the historical wind speed. In optimal power flow calculation, results of Monte Carlo tend to be more concentrated, less volatile in simulation of generating output and branch power. In large numbers of Monte Carlo calculation, using Copula function to model the wind power will be more realistic and accurate to the description of the operation system and characteristics of wind farm outputs. This will provide a guidance for energy-saving dispatching strategy and system operation mode arrangement.

Appendices

Appendix A

Table A1 lists the probability density function (PDF) of each Copula function. Based on those functions, we can obtain parameters of wind speed sample under each Copula function by using parameters estimation method. Here, $\rho$ is linear correlation of two series; k is the degree of freedom in t-distribution; α, θ, λ is parameter of Archimedean Copula.

Table A1 PDF of Copula function

Appendix B

Figure B1 contains P-P plot of each Copula model based on the method in [14].

Fig. B1

P-P plot of each Copula model based on the method in [14]

Appendix C

The objective function in OPF calculation is (C1). Then constraint conditions are (C2).

$${\text{Min}}\;\sum\limits_{{i \in S_{G} }} {(a_{0i} + a_{1i} P_{Gi} + a_{2i} P_{Gi}^{2} )}$$

(C1)

$${\text{s}} . {\text{t}} .\left\{ \begin{aligned} &\varvec{g}(\varvec{\theta},\varvec{V},\varvec{P}_{G} ,\varvec{Q}_{G} ,\varvec{P}_{D} ,\varvec{Q}_{D} ,\varvec{P}_{W} ,\varvec{Q}_{W} ) = {\mathbf{0}} \hfill \\ &{\mathbf{0}} \le \varvec{P}_{G} \le \varvec{P}_{{G_{\hbox{max} } }} \hfill \\ &{\mathbf{0}} \le \varvec{Q}_{G} \le \varvec{Q}_{{G_{\hbox{max} } }} \hfill \\ &{\mathbf{0}} \le \varvec{P}_{D} \le \varvec{P}_{{D_{\hbox{max} } }} \hfill \\ &{\mathbf{0}} \le \varvec{Q}_{D} \le \varvec{Q}_{{D_{\hbox{max} } }} \hfill \\ &\left| {P_{ij} (\varvec{\theta},\varvec{V})} \right| \le P_{{ij_{\hbox{max} } }} \hfill \\ &\varvec{V}_{\hbox{min} } \le \varvec{V} \le \varvec{V}_{\hbox{max} } \hfill \\ \end{aligned} \right.$$

(C2)

where $S_{G}$ is thermal generation set; $P_{Gi}$ is active power of generator i; $a_{0i}$, $a_{1i}$ and $a_{2i}$ are the consumption characteristic curve parameters of generator i; $g( \cdot )$ are power balance equations; $\varvec{\theta}$ and $\varvec{V}$are bus voltage phase angles and amplitudes; $\varvec{P}_{D}$ and $\varvec{Q}_{D}$ are active and reactive load; $\varvec{P}_{W}$ and $\varvec{Q}_{W}$ are active and reactive power output of wind farm; $\varvec{P}_{{G_{\hbox{max} } }}$ and $\varvec{Q}_{{G_{\hbox{max} } }}$ are upper active and reactive power output of thermal generators; $\varvec{P}_{{D_{\hbox{max} } }}$ and $\varvec{Q}_{{D_{\hbox{max} } }}$ are the upper active and reactive load; $P_{ij}$ is active power flow of a line; $P_{{ij_{\hbox{max} } }}$ is the active power upper constraint of a line; $\varvec{V}_{\hbox{max} }$ and $\varvec{V}_{\hbox{min} }$ are upper and lower constraints of system bus voltage.

When the wind farm operates with a constant power factor, the reactive power of wind farm’s export can be calculated like:

$$\varvec{Q}_{W} = \varvec{P}_{W} \tan \varphi$$

(C3)

where $\varphi$ is the power factor angle which is often in the fourth quadrant for grid-tied wind turbine.

Appendix D

Primal-Dual Interior Point Method is usually applied to solving the OPF problem. Then the OPF model of formulas (D1) and (D2) can be described simply as:

$${\text{Min}}\;F(\varvec{P}_{G} )$$

(D1)

$${\text{s}} . {\text{t}} .\left\{ \begin{aligned} \varvec{g}(\varvec{\theta},\;\varvec{V},\;\varvec{P}_{G} ,\;\varvec{Q}_{G} ,\;\varvec{P}_{D} ,\;\varvec{Q}_{D} ,\;\varvec{P}_{W} ,\;\varvec{Q}_{W} ) = {\mathbf{0}} \hfill \\ \varvec{h}(\varvec{\theta},\;\varvec{V},\;\varvec{P}_{G} ,\;\varvec{Q}_{G} ,\;\varvec{P}_{D} ,\;\varvec{Q}_{D} ,\;\varvec{P}_{W} ,\;\varvec{Q}_{W} ) \le {\mathbf{0}} \hfill \\ \end{aligned} \right.$$

(D2)

where $\varvec{h}( \cdot )$ mean inequality constraints.

The process of using dual interior point method to solve OPF problem is: introducing slack variable $\varvec{s}(\varvec{s} > {\mathbf{0}})$, writing the inequality constraints into equality constraints like $\varvec{h} + \varvec{s} = {\mathbf{0}}$, introducing barrier parameter $\varvec{\mu}$, constructing the logarithmic barrier function for slack variable, obtaining augmented Lagrangian function like:

$$L(x) = F -\varvec{\mu}\sum {\ln \varvec{s}} -\varvec{\sigma}^{\text{T}} \varvec{g} -\varvec{\rho}^{\text{T}} (\varvec{h} + \varvec{s})\;$$

(D3)

where $\varvec{\sigma}$ and $\varvec{\rho}$ are dual vector for equality and inequality constraints respectively.