Abstract
Various kinds of new engineering technologies have been studied to realize the low-carbon and sustainable power supply systems all over the world. In actual implementation of these technologies, mostly, there are multiple objectives with trade off relationships among each other, and also various constraints in the achievement of these objectives. Therefore, it should be essential to solve multi-objective optimization problems effectively in the applications of these new technologies in power systems. This paper proposes an improved method to realize multi-objective optimization for critical challenges in advanced power systems. To realize that, in an optimal dispersed generation installation problem, that is, one of effective measures for low-carbon power systems, various optimization methods and their combination methods are evaluated and a hybrid method for evolutionary algorithms was developed. The method can provide improved results compared with other state-of-the-art multi-objective optimization methods.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
As various environmental problems such as climate change due to global warming and air pollution have been real problems, the increasing penetration of renewable energy source (RES) generation which does not produce CO2 and other substances of concern is common critical challenge all over the world. Therefore, many RES generation systems have been installed in various countries and regions, and various subsidies and preferences also have been implemented.
Japan also plans a large number of RES generation system installation and the plan says that more than 20% of total electric power should be generated from RES and most of them should be from dispersed generations (DGs) located in electric power demand areas [1]. Although RES generation is an effective approach in the aspects of CO2 emission reduction, it should be difficult to achieve the grid-parity compared with current generation technologies due to high production cost, low generation efficiency and unstable power capacity etc., despite of many supports from above mentioned subsidies and preferences. The penetration rate of RES is not enough to consider aggressive targets for RES penetration. Therefore, it is important to maximize RES advantages and minimize its disadvantage for the realization of low- carbon society and optimization of multiple objectives with trade-off relationship each other, should be a critical challenge.
In this paper, an effective multiple objectives optimization method is discussed assuming that a distribution power system where many RES DGs are installed. In this discussion, power loss minimization and cost minimization by DG installation are defined as trade-off relation of multiple-objectives because RES DG can reduce CO2 emission itself and power loss reduction by DG can also contribute to CO2 reduction, while RES DG generation cost is expensive compared with conventional power price generally. Then, optimal solutions are derived by simulations using various state-of-the-art optimization techniques. Results are evaluated and discussed and then, a hybrid multi-objective optimization method combining existing effective multi-objective algorithms for novel power systems is proposed.
1.1 Optimization problems in power systems
In order to achieve various purposes and benefits for power systems, a large number of efforts have been provided to the area for effective optimization methods. In all areas of power systems, such as generation, transmission, distribution, and consumption, it is necessary to have appropriate plans to operate, thus it requires optimization tasks under given constraints. In addition, while optimization researches dealt with effective methods for various objectives are important, it should be necessary to evaluate the profitability of new technology implementations considering the shutdown of existing systems and the re-installation of new systems. Generally, the installation benefit and cost have a trade-off relationship and it means that future power systems should be optimized with multi-objectives including the profitability. Therefore, this paper focuses on effective optimization methods not only for the installation benefit of new technology but also for cost minimization.
1.2 Single-objective optimization problems
An optimization problem is to minimize or maximize objective functions under constraints. The problem resolution by optimization methods is one of important measures in real world. General optimization problem has constrains of inequality, equality and upper and lower limit, and it is defined as:
where x = (x 1, x 2,…, x n ) is an n-dimensional vector; f(x) is an objective function; g j (x) ≤ 0 are inequality constraints and h j (x) = 0 are equality constraints; functions f(x), g j (x) and h j (x) are real-valued functions; l i and k i are the upper and the lower bounds of x i , respectively.
Recently, population-based descent method has received many attentions, and differential evolution (DE) and particle swarm optimization (PSO) are major representative examples. In these methods, information of populations composed of solutions is utilized for the creation of new candidates to be compared with current solutions [2]. The outline of these two major algorithms is described.
-
1)
Particle swarm optimization (PSO)
Particle swarm optimization (PSO) is an evolutional computation technique which is inspired by a bird flocking, fish schooling and swarming theory, and utilizes particle swarms flying in problem space, called the hyperspace [3]. In the iteration process, each particle evolves into optimal or optimal approximation solution adjusting its velocity by the information of its best location and best neighbor location on its historical data. Because all particles share information of optimal solutions, PSO provides well convergence in optimal solutions. Therefore, PSO can be used also for various optimization problems in power systems.
With respect to PSO, various improved algorithms are proposed. Constriction factor PSO by Clerc M and Kennedy J [4] is one of PSO subspecies which utilizes constriction factor approach (CFA) controlling the convergence property, and it was reported that the algorithm provided superior results compared with the original PSO using inertia weight (inertia weight approach, IWA) [5, 6].
DE, proposed by Storn and Price, is one of evolution strategies (ES) which is a stochastic direct search method and conducts multi-points search using populations. Although the control of mutation step size is required in ES algorithms, DE does not need to control the step size because it adopts a mathematical operation as its mutation using the weighted sum of the base vector and the difference vectors. As same as PSO, various improved algorithms have been proposed in DE. Adaptive DE is the collective term which shows subspecies of the standard DE algorithm targeting for convergence improvement, and various kinds of adaptive DE algorithms have been proposed. JADE is one of these algorithms and implements the mutation strategy, called the “DE/current-to-pbest” with optional archive and controls scaling factor and crossover rate in an adaptive manner [9]. ε constrained adaptive DE [10] was proposed to improve the scheme proposed in JADE and the ε constrained method, which was the, algorithm to convert unconstrained optimization method into constrained optimization method one using the ε level comparison, was applied.
1.3 Multi-objective optimization problems
An optimization problem for multiple objectives is called a multi-objective optimization problem. In the real world, most optimization problems need to consider multiple objectives. Generally, multi-objective problems are formulated as:
where min f i (x) (i = 1,2,…,n) are objective functions and C(x) is a constraint condition. In a single objective optimization problem, the best value is apparent because it is possible to be compared between two real numbers in size. Generally, there are trade-off relations among objectives in multi-objective optimization problems and thus optimal solution would not be a unique solution but multiple solutions or infinite population. Therefore, optimal solutions cannot improve the value of a certain objective function without degrading some values of the other objective functions would need to be searched, called the Pareto optimal solutions. If Pareto optimal solutions could be searched, the relation of objective functions would be clarified and better decision making could be made. The surface formed by Pareto optimal solutions is called the Pareto front and three aspects are considered to evaluate Pareto front in [11]: 1) the “convergence”, minimizing the distance from search results to the Pareto front; 2) “uniformity”, maintaining uniform solution distribution; 3) “extensity”, maximizing the extent of solutions following the Pareto front.
Recently, the multi-objective evolutional algorithm (MOEA) becomes the active area of research and recent researches focused on the methodology for fast and effective Pareto front provision. Major MOEA methods includes multi-objective particle swarm optimization [12–15], Pareto Envelope based selection (PESA [16] and PESA-II [17]) based on Pareto archived evolution strategy (PAES) [18], and improved PESA-II (IPESA-II [11]). These methods are briefly described below.
-
1)
PAES [18]
The algorithm of PAES starts from initialization of a current solution. Firstly, the current solution is copied and the mutation is executed, and then the generated candidate solution is compared with the current solution. If neither solution dominates, the candidate solution is compared with the population of non-dominant solutions previously archived. Then, one solution which does not dominate others in the least crowded area of the archive is disconnected.
-
2)
Multi-objective PSO
The superior performance of PSO has been utilized not only for single objective optimization but also for multiple-objective optimization in various researches. Reference [12] proposed a multi-objective optimization PSO (MOPSO) algorithm which allows the PSO algorithm to deal with multi-objective optimization problems using an external memory, called the “repository” and [13] introduced a clustering technique which divides particle swarm population, and comparison results with other multi-objective PSO algorithms for some test functions were reported. Also, as application examples for power systems, both [14] and [15] proposed improved approaches of the multi-objective optimization methods for the optimization in energy management system for factories, and voltage and reactive power control, respectively.
-
3)
PESA, PESA-II and IPESA-II
PESA [16] is the multi-objective optimization algorithm integrating the ideas of strength Pareto evolutionary algorithm (SPEA) [19] and PAES [18], which are two major multi-objective optimization methods. PESA uses a population (archive) which stores an approximation to the Pareto front and an internal population which has candidate solutions same as SPEA, and also maintains hypergrid division which can trace the crowded factor of different areas in the archive as same as PAES. PESA-II [17] is the improved version of PESA and mating-selection processes were implemented not in individual based but in region based. Firstly, a hyperbox is selected and then an individual which is the result of evolutional operations is randomly selected from the hyperbox. IPESA-II [11], is an improved version of PESA-II with three improvements: the maintenance method of the archive, individual maintenance around boundary and the selection of the hyperbox by the crowded factor.
2 Effective optimization method in power distribution systems
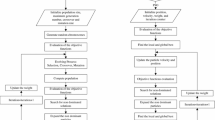
Some preparation tasks for exploring effective optimization method in power distribution systems are conducted, including problem definition, procedure clarification and data preparation.
2.1 Definition of a problem
Many researches have been conducted to solve optimization problems in power system area. Major areas include power system planning and operation, environmentally constrained economic dispatch, state estimation and optimized power flow [20]. For the versatile and essential point of view, benefits or effects maximization of approaches for low-carbon power systems and cost minimization for these approaches should be fundamental trade-off relation objectives. In order to enhance existing power systems into new advanced systems, it must be necessary to achieve both new additional benefit provision to consumers and cost recovery of the investment at the same time. Therefore, this kind of problems is defined as the multi-objective problem in this paper.
The Author's group has conducted some other researches for optimal DG allocations for low-carbon society and it is found that inadequate DG installation would cause power loss increase while effective DG installation would contribute to the realization of very low power loss distribution systems [21]. Therefore, an optimal DG installation is one of critical problems for advanced low- carbon power systems considering most of RES generations, however the correct evaluation of these DGs installation should be the balance of various impacts including cost. In the view of above consideration, this paper deals with optimal DG installation problem considering power loss and cost minimizations. In particular, simulations of power loss and cost reduction by DG location and capacity for a distribution system model are executed and then are evaluated to find the optimal solutions.
2.2 Procedure clarification
Multi-objective optimization would be important in future power systems, because the enhancement of power systems would not be realized only by technical advantages, such as improvement of power supply stability with a large number of RES installations, but their cost effectiveness considering added-values would be essential. In most countries and regions, power systems are already one of social infrastructures and provide values to consumers with reasonable price. Therefore, consumers would not pay additional costs without significant additional values and then multi-objective optimization methods for evaluating the cost effectiveness of enhanced technologies should be critical.
The procedure to find effective solution method for multi-objective optimization problems in power systems is described below. The bi-objective optimization problem of DG allocation with optimal power loss and cost mentioned in above is considered as the base problem in this paper.
-
1)
Distribution model
Considering optimal DG allocation problems, it is necessary to define a target system model firstly. Because many DGs are planned to install into distribution systems in Japan, a model distribution system composed of buses and branches should be defined. In order to calculate power loss in the distribution system model, power flow calculation is necessary, thus active and reactive loads, complex voltage and current at each bus, and branch parameters such as reactance and susceptance are also needed to be prepared. In addition, preconditions and constraints are also necessary to be defined. Constraints can influence the results in optimization problems, thus it is necessary to define specific constraints in power systems especially. These specific constraints include power flow laws, voltage upper and lower limits, and apparent current upper limit, etc.
-
2)
Effective single-objective optimization method in power systems
For the target distribution system with allocated DGs, major single objective optimization algorithms should be used to understand their effectiveness for optimization problems in power systems. As mentioned in above, recently, the population-based descent method has received many attention, thus DE and PSO are selected as base single optimization algorithms in this paper.
In order to evaluate the effectiveness, the number of iterations required for the convergence to the optimal value in an OPF problem can be utilized. With respect to the optimal value compared by some candidate algorithms, the pre-calculated exact solution is used. As candidate algorithms, not only original DE and PSO algorithms, but also subspecies of these algorithms are considered. Then, the best algorithm in these simulations will be selected as the best single objective optimization algorithms for optimization problems in power systems.
-
3)
Enhancement of the effective single-objective optimization method for multi-objective optimization problems in power systems
Multi-objective optimization algorithm is considered on the enhancement of the effective single -objective optimization algorithm selected in the previous step. Considering the enhancement of the effective single objective optimization method, various hybrid approaches using proven major multi-objective algorithms should be discussed. In case that Pareto front would be evaluated on the three aspects: “convergence”, “uniformity” and “extensity”, it was assumed that each multi-objective optimization method had specific ranges in which high quality Pareto front was provided by pre-conducted basic researches and simulations. Therefore, it is expected that the hybrid approach of proven multi-objective algorithms can provide an effective Pareto front for the multi-objective optimization problems in future power systems. Then, the algorithm which finds the best Pareto front in the aspects of “convergence”, “uniformity” and “extensity” will be selected as the best multi-objective optimization algorithm.
2.3 Data preparation
Some predefined data for simulations are provided. The data include target distribution system model and defined data, constraints, and cost related data.
-
1)
Distribution system model
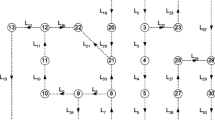
As a distribution system model for simulations, the wiring diagram of grid in [22], which is the radial distribution system model and has 126 buses is selected, as shown in Fig. 1.
The bus number 126 is the slack bus and it is found that the slack bus provides active power of P = 4.4239(p.u.) and reactive power Q = 3.1053(p.u.) for the total load of P = 4.2300(p.u.) and Q = 2.8870(p.u.). Therefore, total power loss is calculated as P loss = 0.1939(p.u.) and Q loss = 0.2183(p.u.) and power loss rate for injected power at slack bus are P: 4.383%, Q: 7.030%, respectively. Parameters for the system model such as branch attributes, load at bases were also referred to [22].
-
2)
Constraint definition for optimization problem
With respect to the installation of DGs, the following constraints are defined.
-
a.
The number of installation DGs is 2, 3 and 4.
-
b.
DG would be installed at one of the buses.
-
c.
One DG would be installed per one part where the load would be installed in the same range.
Capacity constraints for each DG and slack bus are shown in Table 1.
-
3)
Cost related data
As an additional objective, “cost minimization” is required for the consideration of multi-objective optimization. Table 2 shows installed DGs and cost parameters used in the simulation. In the table, “variable cost: 0.5 per p.u.” means that required cost per DG capacity 1 p.u. is 0.5 p.u.
-
4)
Calculation result of power flow by interior point method
Before the discussion using simulations, OPF calculation for the defined problem is executed using an interior point method to know exact optimal solutions. Table 3 shows calculation results of the OPF. The leftmost column shows the name of installed DG and DG location, active and reactive power capacities are provided by the number of total DG in the distribution model. For example, when the number of installed DGs is 2, the location of the DG-1 is Bus7 and active and reactive powers are 1.983168 (p.u.) and 1.022116 (p.u.), respectively.
3 Simulation of single-objective optimization
For the exploring effective methods for optimization problems in power systems, the effective single-objective optimization problem is considered.
3.1 Application of proven optimization algorithms
The following major algorithms are prepared to conduct simulations and each algorithm is named after considering its characteristics, base algorithms and objective function for clear identification.
-
1)
Original PSO [4] (“IWA-PSO-OPF”);
-
2)
Constriction factor PSO [6] (“CFA-PSO-OPF”);
-
3)
Original DE [7] (“ODE-OPF”);
-
4)
Adaptive DE [10] (“ADE-OPF”).
3.2 Simulation results of single-objective algorithms
Simulation results of the convergence status for single -objective optimization algorithms are provided. Utilized algorithms are assumed to be effective for the power system problems. In each simulation process, if the new solution would be predominant compared with the current solution, the optimal solution is replaced and the non-dominant process is discarded. The number of iterations is 100 and the number of populations (swarms or archives) is 20 in each simulation result.
-
1)
PSO
Firstly, the simulation using “IWA-PSO-OPF” was executed. Figure 2 shows simulation results for the convergence status of optimal value by “IWA-PSO-OPF”. Predominant values are converged with around 60 iterations for 2 and 3 DGs and around 90 iterations for 4 DGs.
Then, the simulation using “CFA-PSO-OPF” was executed. Figure 3 shows the simulation result for the convergence status of optimal value by “CFA-PSO-OPF”.
Predominant values are converged with around 20 iterations for 2 DGs and around 80 iterations for 3 and 4 DGs. However, convergence rates to optimal values for all 3 patterns are fast compared with “IWA-PSO-OPF”, and it is found that better approximation optimal could be retrieved with small number of iterations.
-
2)
DE
Next, the simulation using “ODE-OPF” was executed. Figure 4 shows simulation results for the convergence status of optimal value by “ODE-OPF”. Predominant values are converged with around 30 iterations for 2 DGs, around 60 iterations for 3 DGs and around 90 iterations for 4 DGs. The performance of “ODE-OPF” is in the same range as “IWA-PSO-OPF” but inferior to “CFA-PSO-OPF”.
Finally, the simulation using “ADE-OPF” was executed. Figure 5 shows simulation results for the convergence status of optimal value by “ADE-OPF”.
Predominant values are converged with around 20 iterations for 2 DGs, around 40 iterations for 3 DGs and around 50 iterations for 4 DGs. In addition, convergence rates to optimal values for all 3 patterns are fast compared with other three algorithms, and “ADE-OPF” provides the best performance among 4 algorithms in our simulation results.
3.3 Discussion of simulation results
Single-objective optimization simulations were executed with PSO and DE algorithms which were assumed to be effective for power system related problems and the adequacy of these algorithms were discussed for power systems. Summaries of these simulations are presented as follows.
-
1)
All 4 utilized algorithms can provide good performance for the convergence of predominant solutions and it is confirmed that “CFA-PSO-OPF” and “ADE-OPF”, which are subspecies of original OPF and DE algorithms, respectively, provide better performance compared with original algorithms.
-
2)
“ADE-OPF” is one of adaptive DE algorithms with adequately the highest performance.
-
3)
Because the objective function “Power loss minimization by DGs” is a constrained optimization problem, it is confirmed that these four algorithms can be used for constrained optimization problems.
4 Multi-objective optimization problems in power systems
By the enhancement of the effective single objective optimization method, an effective multi-objective optimization method is considered for the evaluation of future advanced power system.
4.1 Enhancement for the application of single objective optimization problem
The enhancement of “ADE-OPF” which has confirmed its effectiveness for single-objective optimization problem in power systems was considered to be applied for multi-objective problems.
In the consideration, a methodology which manages multi-objective space efficiently and finds a good approximation set of the Pareto front should be required. Therefore, the utilization of the archive method in the PAES [18], which is called the “PAES-Archive method” in this paper, was used for the effective management of solutions generated in multi-objective space by “ADE-OPF”.
In order to confirm the applicability of “ADE-OPF” to multi-objective optimization problems, some simulations of hybrid approach of “ADE-OPF” and “PAES-Archive method” were conducted by changing parameters, such as the number of generations and individuals. Figure 6 shows a reference example which is one of the simulation results of this approach, with the number of DGs: 3, generations: 40 and individuals: 80. In this chart, no solution exists in some ranges and solutions are not provided uniformly. Like this chart, it is difficult to obtain a better Pareto front which has enough quality in aspects of “convergence”, “uniformity” and “extensity” in our numeral simulations with these simulations. Although a brief trend of the Pareto front in the optimization problem can be found from this sample chart, in some simulation results, only a few solutions were able to be selected thus Pareto front was not able to be drawn.
4.2 Challenges in hybrid approach of optimization methods
In order to solve the challenge in the hybrid approach of “ADE-OPF” and “PAES-Archive method”, another hybrid approach with other multi-objective optimization methods was considered.
-
1)
Utilization of the adaptive grid in IPESA-II
Grid division of an objective space was proposed in PESA-II [18] to maintain diversity of solutions, and this method has changed the existing individual-based selection process to the area-based selection process. IPESA-II [11], which is the enhanced version of PESA-II improved results by changing the adjusting method in the grid environment. Therefore, utilization of the adaptive grid method in the IPESA-II, which is called the “Adaptive-Grid method” in this paper, was considered for the effective management of solutions generated in multi-objective space by “ADE-OPF”.
-
2)
Pareto front creation with the hybrid approach of “ADE-OPF” and “Adaptive-Grid method”
In order to consider the hybrid approach of “ADE-OPF” and “Adaptive Grid method”, some basic simulations were executed by changing some parameters. As the result, the following issue was clarified in our numeral simulations.
-
a.
The mating-selecting method utilized in IPESA-II to create solutions in multi-objective space could not find Pareto front solutions effectively if enough solutions would not exist in the space.
Therefore, the following conditions were added to the hybrid approach.
-
b.
If solutions in adaptive grid in the multi-objective space would be smaller than 2, “ADE-OPF” would be utilized to create solutions in the space, otherwise mating-selection would be utilized.
Since the method was a hybrid approach of “ADE-OPF” and IPESA-II [11], the method is called the hybrid ADE-IPESA-II (H-ADE-IPESA-II) in this paper.
-
3)
Optimization testing using H-ADE-IPESA-II method
Using H-ADE-IPESA-II, Pareto front for the multi-objective optimization problem was able to be found effectively.
Figure 7 shows the Pareto front of the multi-objective optimization problem which has two objectives of loss minimization and cost minimization with effective DG installation (3 DGs) using H-ADE-IPESA-II. A good set of the Pareto front was provided with respect to “convergence”, “uniformity” and “extensity”. Although the number of DGs in Fig. 8 is 3, other cases (DGs = 2, 4) also provided similar good results.
From the result, H-ADE-IPESA-II which is hybrid approach of Adaptive DE and IPESA-II is one of effective methods for constrained multi-objective optimization problems in power systems.
4.3 Discussion of multi-objective optimization results
Using H-ADE-IPESA-II, various simulation scenarios for the multi-objective optimization problem were executed. Three simulation parameters for the minimization of power loss were considered by the installation of DGs: a. Variable cost; b. Fixed and variable cost; c. Discrete DG capacity.
-
1)
Optimization of power loss and cost by the installation of 3 DGs considering variable cost
Figure 7 shows the Pareto front of both loss and cost optimization problem and only variable cost is considered using the proposed H-ADE-IPESA-II.
-
2)
Optimization of power loss and cost by the installation of 3 DGs considering both fixed and variable cost
With respect to objective function for cost, both fixed and variable costs are considered and the Pareto front is created.
Figure 8 shows the Pareto front of the multi-objective optimization problem considering both fixed and variable costs. Under the influence of the fixed cost, the set of Pareto front does not converge to a single curve, but shows divided lines.
-
3)
Optimization of power loss and cost by the installation of 3 DGs considering discrete DG capacity
With respect to objective function for loss minimization, discrete DG capacity settings are considerable. Therefore, the Pareto front using discrete DG capacity settings are also considered.
Figure 9 shows the Pareto front of the multi-objective optimization problem for discrete DG capacity settings with variable cost only. Figure 10 shows the Pareto front of the multi-objective optimization problem for discrete DG capacity settings over non-discrete DG capacity setting with both fixed and variable cost. Basically, the Pareto front for the problem with discrete DG capacity settings does not show a clear difference from that with non-discrete DG capacity setting.
5 Conclusions
In many regions and countries, huge investment has been made for electric power, and power systems are one of important social infrastructures. Because most people in the regions and countries can adequately use electricity, the cost reduction is one of major requirements recently. It is necessary to enhance current power systems into advance clean and sustainable systems considering current some environmental issues. Therefore, utility companies are required to deal with such benefit and cost optimization problems with trade-off relationships in their objectives.
This paper provides effective tools for multi-objective optimization problems which are essential conditions for problems in power systems, and thus many researches considering new tool development have been conducted.
Because most of multi-objective optimization tools are prepared for non-constrained problems, it is difficult to have adequate results for constrained problems using most of these methods in convergence, uniformity and extensity. In order to solve that, adequate results can be provided by the hybrid approach between adaptive DE method and IPESA-II. Although this paper dealt with only two objective optimization problems, it is assumed that the approach can be applied to more than 3 objectives optimization problems and these problems are conducted in future work. In addition, test data are used in all simulations in this paper, but real multi-objective optimization problems should have additional constraints related to electrical and economical aspects. Therefore, results of the Pareto front provided by the proposed approach and actual decisions made in some actual projects are also needed to be compared in the future.
References
The Study Group on Low Carbon Power Supply System (2009) Establishing a low carbon power supply system. Ministry of Economy, Trade and Industry (METI) (in Japanese). http://www.meti.go.jp/report/data/g90727ej.html. Accessed 1 May 2014
Takahama T (2007) Optimization by population-based descent method—differential evolution and particle swarm optimization. Hiroshima City University, Hiroshima (in Japanese)
Kennedy J, Eberhart R (1995) Particle swarm optimization. In: Proceedings of the IEEE international conference on neural networks, Vol 4, Perth, WA, 27 Nov–1 Dec 1995, pp 1942–1948
Clerc M, Kennedy J (2002) The particle swarm—explosion, stability, and convergence in a multidimensional complex space. IEEE Trans Evolut Comput 6(1):58–73
Fukuyama Y (2004) Comparative studies of particle swarm optimization techniques for reactive power allocation planning in power systems. IEEJ Trans Power Energy 124(5):690–696 (in Japanese)
Eberhart RC, Shi Y (2000) Comparing inertia weights and constriction factors in particle swarm optimization. In: Proceedings of the 2000 congress on evolutionary computation (CEC’00), Vol 1, La Jolla, CA, 16–19 Jul 2000, pp 84–88
Storn R, Price K (1996) Minimizing the real functions of the ICEC’96 contest by differential evolution. In: Proceedings of the international conference on evolutionary computation, Nagoya, 20–22 May 1996, pp 842–844
Storn R, Price K (1997) Differential evolution—a simple and efficient heuristic for global optimization over continuous spaces. J Global Optim 11(4):341–359
Zhang JQ, Sanderson AC (2009) JADE: adaptive differential evolution with optional external archive. IEEE Trans Evolut Comput 13(5):945–958
Takahama T, Sakai S (2010) Efficient constrained optimization by the ε constrained adaptive differential evolution. In: Proceedings of the IEEE 2010 congress on evolutionary computation (CEC’10), Barcelona, 18–23 Jul 2000, 8 pp
Li MQ, Yang SX, Liu XH, et al (2013) IPESA-II: Improved Pareto envelope-based selection algorithm II. In: Proceedings of the 7th international conference on evolutionary multi-criterion optimization (EMO’13), Sheffield, 19–22 Mar 2013, LNCS 7811, pp 143–155
Coello CA, Lechuga MS (2002) MOPSO: a proposal for multiple objective particle swarm optimization. In: Proceedings of the IEEE congress of evolutionary computation (CEC’02), Vol 2, Honolulu, HI, 12–17 May 2002, pp 1051–1056
Pulido GT, Coello CA (2004) Using clustering techniques to improve the performance of a particle swarm optimizer. In: Proceedings of the genetic and evolutionary computation conference (GECCO’04), Seattle, WA, 26–30 Jun 2004, pp 225–237
Kitamura S, Mori K, Sindo S et al (2005) Modified multi-objective particle swarm optimization method and its application to energy management system for factories. IEEJ Trans Electron 125(1):21–28 (in Japanese)
Iwasaki K, Aoki H (2007) Voltage and reactive power control using multiple objective optimization method with PSO. Proc Sch Eng Tokai Univ 47(2):49–54 (in Japanese)
Corne DW, Knowles JD, Oates MJ (2000) The Pareto envelope-based selection algorithm for multiobjective optimization. In: Proceedings of the 6th international conference on parallel problem solving from nature (PPSN’00), Paris, 18–20 Sept 2000, LNCS 1917, pp 839–848
Corne DW, Jerram NR, Knowles JD, (2001) PESA-II: region-based selection in evolutionary multiobjective optimization. In: Proceedings of the genetic and evolutionary computation conference (GECCO’01), San Francisco CA, 7–11 Jul 2001, pp 283–290
Knowles J, Corne D (1999) The Pareto archived evolution strategy: A new baseline algorithm for multiobjective optimization. In: Proceedings of the 1999 congress on evolutionary computation (CEC’99), Vol 1, Washington, DC, 6–9 Jul 1999, pp 98–105
Zitzler E, Thiele L (1999) Multiobjective evolutionary algorithms: a comparative case study and the strength Pareto approach. IEEE Trans Evolut Comput 3(4):257–271
Rivas-Davalos F, Moreno-Goytia E, Gutierrez-Alcaraz G, et al (2007) Multiobjective optimization challenges in power system: the next step forward. In: Proceedings of the electronics, robotics and automotive mechanics conference (CERMA’07), Morelos, Mexico, 25–28 Sept 2007, pp 681–686
Kuroda K, Magori H, Yokoyama R et al (2012) Optimal allocation of dispersed generations in distribution networks to realize low-carbonate power system. Power Syst Technol 36(12):1–10 (in Chinese)
Yang H, Wen FS, Wang LP, et al (2008) Newton-downhill algorithm for distribution power flow analysis. In: Proceeding of the 2nd IEEE international conference on power and energy (PECon’08), Johor Bahru, 1–3 Dec 2008, pp 1628–1632
Author information
Authors and Affiliations
Corresponding author
Additional information
CrossCheck date: 19 November 2014
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
KURODA, K., MAGORI, H., ICHIMURA, T. et al. A hybrid multi-objective optimization method considering optimization problems in power distribution systems. J. Mod. Power Syst. Clean Energy 3, 41–50 (2015). https://doi.org/10.1007/s40565-015-0096-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40565-015-0096-0