Abstract
The design of electrical layout is a key element in the offshore wind farm planning. We present a novel electrical layout design optimization method for offshore wind farms in this paper. The proposed method can be used to generate the network model based on fuzzy c-means (FCM) and binary integer programming (BIP) methods. It can automatically allocate wind turbines to the nearest substations and obtain the topology structure of cables utilized to connect wind turbines or turbine and substation. The objective of this optimization is to minimize the investment costs of cable connection and the transmission power losses. The results of case study clearly demonstrated the feasibility of the proposed method and showed that it can be used as a reliable tool for electrical layout design of offshore wind farms.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
During these years, the interest in the utilization of wind power is increasing significantly worldwide [1, 2]. Generally, a wind farm could be located onshore or offshore. In recent years, the offshore wind farm appears to be more advantageous and has experienced significant growth since better wind powers are available offshore compared to those on land [3–5]. However, due to the large capacity of offshore wind farms and the long distance to shore, and also the variable wind conditions, the investment costs for offshore wind power are much higher than those for onshore installations and operations. Unlike traditional power generating plants which are built around a few high rating generators within a centralized location, offshore wind farms aggregate the power generated by a great variety of small wind powered generators spread out over a large area. The energy generated by each wind turbine is collected and transferred to a substation via a network of cables, called a collector system. The increasing size of the wind farms has led to a problem of finding a suitable cable connection scheme which must consider the economical and operational needs simultaneously [6]. Therefore, the electrical layout plays a very important role in the offshore wind farm system.
Generally, there are many factors in the design and layout of offshore wind farms, such as terrain, wind turbine locations, reliability, power losses, economics, landowner requirements, and climate [7]. In a collector system, the electrical power losses impact the economic evaluation of wind farm operation primarily. Intuitively, to lower power losses, the cable lengths should be shorter. However, shortening cable lengths may not always be possible due to the constraints of network reliability, terrain, landowner’s requirement, etc. This paper focuses on the cable topology design among wind turbines and substations with the objective to minimize the overall investment costs of cable connection and the power losses cost considering the network reliability constraints.
In a large and complex engineering system, such as a wind farm, clustering is an effective way to reduce the complexity of the model. It is the process of grouping a data set in a way that the similarity between data within a cluster is maximized while the similarity between data of different clusters is minimized [8]. Although it has been used in earlier research works on wind turbines, there has no research and application for electrical layout design. For instance, in [9], a clustering algorithm was used to group wind turbines based on power output dynamics. Normally, there are two popular approaches to clustering. One is crisp clustering (or hard clustering), and the other one is fuzzy clustering [10]. In the crisp clustering method, the boundary between clusters is fully defined. However, in many practical cases, boundaries between natural classes may be overlapping. Thus certain input patterns do not completely belong to a single class, but partially belong to the other classes too. In such cases, the fuzzy clustering method (FCM) provides a better and more useful method to classify these patterns. FCM is a data clustering method in which a dataset is grouped into N prespecified clusters, with every data point in the dataset belonging to every cluster to a certain degree [11]. By iteratively updating the cluster centers as well as the membership grades for each data point, FCM moves the cluster centers to the right location within the dataset. However, it is worth noting that the unsupervised clustering algorithms are not preferable in determining the number of hidden layer clusters, especially when dealing with complex data distribution. In this paper, based on FCM, a fuzzy clustering method is adopted to allocate wind turbines to their nearest substations automatically.
This paper is structured as follows. First, the state of the art of the problem is concisely reviewed. Then, the mathematical model of proposed electrical layout design optimization is presented. After that, the methodologies applied into the proposed model will be described, together with the implementation details. Finally, the numerical simulations are presented and conclusions extracted by discussing the proposed methods and the results.
1.1 The proposed optimization model
The problem can be modeled as:
1.2 Objective
With the aim of studying large-scale electrical layout of an offshore wind farm, this model is proposed as a multi-objective optimization problem, which is to minimize the annual investment cost C inv and transmission power losses cost C losses simultaneously.
where \( \varvec{x} = \{ x_{ij} \left| {i \in [1,N]} \right.,{\kern 1pt} {\kern 1pt} j \in [1,N]\} \) is the set of decision variables x ij ∈ {0, 1} to specify whether connect the cable between bus i and bus j; N is the total number of wind turbine buses; c inv is the investment cost ($/m) of cable connection; c loss is the levelized transmission power losses cost ($/kWh); l ij is the length of cable between buses i and j; T is the number of periods; and \( pl_{ij}^{t} \) is the power losses of cable between buses i and j in period t.
1.3 Constraints
According to the complexity of power network topology and power system operation reliability, the electric network characteristics should be taken into consideration. In the proposed model, the minimization of the objective function is subject to operational constraints, which are active and reactive power flow constraints, capability limits of the cables, voltage limits for all the buses, radiality constraints. And these constraints can be formulated as follows:
-
(i)
Active power flow constraints:
$$ P_{i}^{g} = \sum\limits_{j = 1}^{N} {V_{i} } V_{j} (G_{ij} \cos (\delta_{i} - \delta_{j} ) + B_{ij} \sin (\delta_{i} - \delta_{j} )) $$(6) -
(ii)
Reactive power flow constraints:
$$ Q_{i}^{g} = \sum\limits_{j = 1}^{N} {V_{i} } V_{j} (G_{ij} \sin (\delta_{i} - \delta_{j} ) - B_{ij} \cos (\delta_{i} - \delta_{j} )) $$(7) -
(iii)
Capability limits of cables:
$$ \left| {S_{ij} } \right| \le S_{\hbox{max} } ,\quad \forall i \in N $$(8) -
(iv)
Bus voltage limits:
$$ V_{\hbox{min} } \le V_{i} \le V_{\hbox{max} } ,\quad \forall i \in N $$(9)$$ \delta_{\hbox{min} } \le \delta_{i} \le \delta_{\hbox{max} } ,\quad \forall i \in N $$(10) -
(v)
Radial constraints:
$$ \sum\limits_{i = 1,i \ne j}^{N} {x_{ij} } \le 1,\quad \forall j \in N$$(11)where \( P_{i}^{g} \) and Q g i are active and reactive power outputs of wind turbines in bus i; V i and δ i are voltage magnitudes and angles of bus i; G ij and B ij are the real and imaginary terms of the element i, j in bus admittance matrix; S ij is the apparent power flow in the cable between buses i and j; Smax, Vmin, Vmax, δmin, and δmax are the corresponding lower and upper limits of these variables, respectively.
2 Methodologies
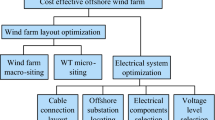
The flowchart in Fig. 1 illustrates the proposed method for the optimal design of electrical layout for an offshore wind farm.
2.1 Wind turbine allocation using fuzzy c-means clustering
Fuzzy c-means (FCM) clustering algorithm is one of the most important and popular fuzzy clustering algorithms. It allows one piece of data point to one or more cluster centers. This algorithm is frequently utilized in pattern recognition [10]. For some clustering methods, including FCM, the number of clusters k needs to be given in advance. By iteratively updating the cluster centers as well as the membership grades for each data point, FCM moves the cluster centers to the right location within the dataset.
Suppose a collection of data points Y = {y1, y2, …, y n }, n is the number of elements in the dataset. The set is divided into k clusters (1 < k < n), and \( C = \{ c_{ij} \left| {i \in [1,n],\;j \in [1,k]} \right.\} \) is the cluster center matrix. The membership matrix indicating the subordination degree of ith element to jth element is \( U = \{ u_{ij} \left| {i \in [1,n],\;j \in [1,k]} \right.\} \).
The FCM algorithm performs clustering by solving
where m is the weighted index; J m is the center of each data point to the class and the square of the Euclidean distance.
The algorithm is composed of the following steps:
-
Step-1 Give the number of clusters k, the weighted index m, and the iterative standard ɛ.
-
Step-2 Fix the membership matrix U with a random number between 0 and 1. Set the iteration number t = 1.
-
Step-3 Calculate the cluster center C
$$ c_{i} (t) = {{\left( {\sum\limits_{j = 1}^{m} {u_{ij}^{m} (t)x_{ij} (t)} } \right)} \mathord{\left/ {\vphantom {{\left( {\sum\limits_{j = 1}^{m} {u_{ij}^{m} (t)x_{ij} (t)} } \right)} {\left( {\sum\limits_{j = 1}^{m} {u_{ij}^{m} (t)} } \right)}}} \right. \kern-0pt} {\left( {\sum\limits_{j = 1}^{m} {u_{ij}^{m} (t)} } \right)}} $$(16) -
Step-4 Calculate the new membership matrix U
$$ u_{ij} (t) = \sum\limits_{i = 1}^{k} {\left( {d_{ij} (t - 1)/d_{rj} (t - 1)} \right)^{2(m - 1)} } $$(17)where \( d_{ij} = \left\| {\user2{x}_{i} - \user2{c}_{j} } \right\| \) is the Euclidean distance between \( \user2{x}_{i} \) and \( \user2{c}_{j} \).
-
Step-5 Calculate the objective function J m . If the maximum of iterations is reached or stop criterion. \( \left\| {u_{ij} \left( t \right) - u_{ij} \left( {t - 1} \right)} \right\| \le \varepsilon \) is met, then stop; otherwise, return to step-3.
It can be seen that the entire optimization process is to revise the cluster centers and the membership degrees repeatedly until satisfying the stop criterion. The FCM algorithm has been collected in the fuzzy logic toolbox in MATLAB. In this paper, based on FCM, a fuzzy clustering approach is adopted to automatically allocate N wind turbines to S substations, where we prespecified the number of substations N and the number of wind turbines S and their Cartesian coordinate locations (X, Y) in an offshore wind farm.
2.2 Wind turbine reallocation using binary integer programming algorithm
Binary integer programming (BIP) algorithm is a special case of Linear Programming (LP) where the variables have only 0–1 binary integer values. Based on FCM, all the wind turbines could be allocated to their nearest substations respectively. However, with the aim of considering network operation reliability constraints, the capacity of connected turbines in one substation is limited, and each turbine should belong to a single substation. Therefore, in this phase, a maximum problem with BIP constraints is developed. The objective function here is to maximize the overall membership degree calculated from FCM and reallocate turbines to their nearest substations while satisfying the capacity limits.
With the above considerations, the BIP model for finding the optimal turbine allocation could be formulated as:
where u ij is the membership degree calculated from FCM; z ij is the binary decision variables indicating whether turbine i is allocated to substation j; Nwt and Ns are the number of wind turbines and substations, respectively; and NWTmax is the maximum number of wind turbines in one substation.
BIP problem is NP-hard and can be solved by methods like Branch and Bound (BNB) and Gomory Cut algorithms [12]. In this paper, we solved BIP with BNB method, which can be utilized from the optimization toolbox of MATLAB.
2.3 Cable layout optimization using minimum spanning tree algorithm
The problem of the optimal design of electrical layout for an offshore wind farm can be considered as finding a tree to meet required design characteristics in a graph G = (V, E), where V is the set of vertices and E is the set of edges. Considering the radiality constraints for the network topology, a cable layout optimization method is proposed based on the Minimum Spanning Tree (MST) algorithm. MST constructs a tree of minimum total length between specified nodes, where the tree is defined as a graph G with one and only one path between every two nodes. Therefore, MST algorithm can be used to address the problem of finding the minimum total length layout design for cable connection in a wind farm, where the minimum total length gives the minimum total investment for cable connection which relies on the cable length, and the wind turbines’ locations are the nodes.
There are now three commonly used MST algorithms, which are Boruvka’s algorithm, Kruskal’s algorithm and Prim’s algorithm [13]. In our work, Prim’s algorithm is utilized to find the optimal layout, which is a greedy algorithm that finds a minimum spanning tree for a connected weighted undirected graph. It finds a subset of the edges that forms a tree that includes every vertex, where the total weight of all the edges in the tree is minimized. This algorithm works by attaching a new edge to a single growing tree at each step: start with any vertex (arbitrary one) as a single-vertex tree; then add V-1 edges to it, always taking next minimum-weight edge that connects a vertex on the tree to a vertex not yet on the tree. The process is repeated until all the vertices are included in the spanning tree. After that, the transmission power losses can be obtained according to the optimal cable layout solution.
2.4 Case study
The proposed algorithms have been tested on an example of 150 MW offshore wind farm consisting of fifty 3 MW wind turbines. The Vestas V112 3 MW offshore wind turbine [14] is selected here. The cut-in, cut-out, and rated speeds of this type of turbine are 3, 25, and 12 m/s respectively, and the mechanical power captured by a given wind turbine is a function of wind speed, which is shown in Fig. 2. The historical wind data in one year was obtained from one wind observation station, which was provided by the Australian Bureau of Meteorology [15]. The wind speed distribution and Weibull fitting are given in Fig. 3. Some of the common cable sizes used in large-scale offshore wind farms can be found in [16]. In this paper, the electric parameters of chosen cable HEPRZ1 18/30 kV 1 × 400 mm2 are tabulated in Table 1.
Optimal wind turbine placement considering effects of local wind patterns, land topography, wind turbine wake effects is a widely researched area. Therefore, for the purpose of this work, it has been assumed that the wind turbine locations in the wind farm are already available, which has been justified by the availability of abundant literature in this area [17]. It is also assumed that the availability of these wind turbines is 100% here, and the bus voltage level is set to be 33 kV. The capacity for one substation is 75 MW.
The optimal electrical layout scheme is illustrated in Fig. 4. It shows 3 substations formed containing 25 wind turbines respectively. The black dots are the locations of turbines while the red ones are locations of substations. And the blue lines are the optimal cable connections. Note that the totally layout boundary of the wind farm is 4 km, and the farm area is 16 km2. The simulation result is shown in Table 2.
The total length of optimal cables is 31.4 km and the average power loss in the cables is 50 kW, which is 0.04% of the installed wind farm capacity. Although the network power loss cost is high, when spread out over the lifetime of the cables, the annual costs do not vary significantly.
3 Conclusion
Electrical layout design for an offshore wind farm is presented in the paper. The proposed method can be used to generate the network model based on fuzzy c-means clustering (FCM) and binary integer programming (BIP) methods, which can automatically allocate wind turbines to their nearest substations and obtain the topology structure of cables which are utilized to connect turbines or turbine and substation. The objective of the optimization is to minimize the annual investment costs of cable connection and transmission power losses. The Minimum Spanning Tree (MST) algorithm is utilized to optimize the electrical layout while satisfying the network radial constraint. The results of case study clearly demonstrated the feasibility of the proposed method and showed that it can be used as a reliable tool for electrical layout design of offshore wind farms.
References
Kaboouris J, Kanellos FD (2010) Impacts of large-scale wind penetration on designing and operation of electric power systems. IEEE Trans Sustain Energy 1(2):107–114
Yao F, Dong ZY, Meng K et al (2012) Quantum-inspired particle swarm optimization for power system operations considering wind power uncertainty and carbon tax in Australia. IEEE Trans Ind Inform 8(4):880–888
Dong ZY, Wong KP, Meng K et al (2010) Wind power impact on system operations and planning. In: Proceedings of the 2010 IEEE power and energy society general meeting (PES’10), 25–29 July 2010, Minneapolis, MN, USA, 5 pp
Torres-Olguin RE, Molinas M, Undeland T (2012) Offshore wind farm grid integration by VSC technology with LCC-based HVDC transmission. IEEE Trans Sustain Energy 3(4):899–907
Fuglsang P, Thomsen K (1998) Cost optimization of wind turbines for large scale off-shore wind farms. RisØ-R-1000(EN), RisØ National Laboratory, Roskilde, Denmark
Dutta S, Overbye TJ (2012) Optimal wind farm collector system topology design considering total trenching length. IEEE Trans Sustain Energy 3(3):339–348
Camm EH, Behnke MR, Bolado O et al (2009) Wind power plant collector system design considerations: IEEE PES wind plant collector system design working group. In: Proceedings of the 2009 IEEE power and energy society general meeting (PES’09), 26–30 July 2009, Calgary, Canada, 7 pp
Kwok T, Smith KA, Lozano S et al (2002) Parallel fuzzy c-means clustering for large data sets. In: Proceedings of the 8th international Euro-Par conference on parallel processing (Euro-Par’02) 27–30 Aug 2002, Paderborn, Germany, LNCS 2400, pp 365–374
Ma Y, Jiang JN, Runolfsson T (2011) Cluster analysis of wind turbines of large wind farm. In: Proceedings of the 2009 IEEE PES power systems conference and exposition (PSCE ‘09), 15–18 March 2009, Seattle, WA, USA, 7 pp
Duda RO, Hart PE (1974) Pattern classification and scene analysis. Wiley, New York, NY, USA
Bezdek J, Ehrlich R, Ful W (1984) FCM: the fuzzy c-means clustering algorithm. Comput Geosci 10(2/3):191–203
Halperin D, Overmars MH, Sharir M (1992) Efficient motion planning for an L-shaped object. SIAM J Comput 21(1):1–23
Sedgewick R, Flajolet P (1995) An introduction to the analysis of algorithms. Addison-Wesley Professional, Boston, MA, USA
D’Souza N, Gbegbaje-Das E, Shonfield P (2011) Life cycle assessment of electricity production from a Vestas V112 turbine wind plant. Final report, PE North West Europe ApS, Copenhagen, Denmark
Australian Bureau of Meteorology. http://www.bom.gov.au
Al-Mokha 60 MW wind farm project (MWFP). Final report, E2811 V2, Ministry of Electricity & Energy, Republic of Yemen (2010)
Han X, Guo J, Wang P (2012) Adequacy study of a wind farm considering terrain and wake effect. IET Gener Transm Dis 6(10):1001–1008
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This article is published under license to BioMed Central Ltd. Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Chen, Y., Dong, Z., Meng, K. et al. A novel technique for the optimal design of offshore wind farm electrical layout. J. Mod. Power Syst. Clean Energy 1, 258–263 (2013). https://doi.org/10.1007/s40565-013-0035-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40565-013-0035-x