Abstract
The power grid in a typical micro distribution system is non-ideal, presenting itself as a voltage source with significant impedance. Thus, grid-connected converters interact with each other via the non-ideal grid. In this study, we consider the practical scenario of voltage-source converters connected to a three-phase voltage source with significant impedance. We show that stability can be compromised in the interacting converters. Specifically, the stable operating regions in selected parameter space may be reduced when grid-connected converters interact under certain conditions. In this paper, we develop bifurcation boundaries in the parameter space with respect to Hopf-type instability. A small-signal model in the dq-frame is adopted to analyze the system using an impedance-based approach. Moreover, results are presented in design-oriented forms so as to facilitate the identification of variation trends of the parameter ranges that guarantee stable operation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Three-phase pulse-width-modulated (PWM) voltage-source converters (VSCs) operating in rectifier mode have become a popular choice for ac-dc power conversion in many medium to high power applications. Due to the many desirable features that the VSC offers, e.g., low current harmonics, controllable power quality, and high efficiency, the VSC has been used in a variety of industrial and commercial applications, such as un-interruptible power supply systems, power supplies for telecommunication equipment, HVDC systems, distributed energy sources for renewable energy generation, battery storage systems, power conversion systems for process technology, and so on [1]. In most of these applications, the VSC does not only function as a high-performance power load to the ac power source, but also a reliable interface for many power conversion systems with the ac source.
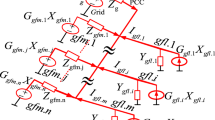
As possibilities of applications of VSCs increase, it can be appreciated that multiple VSCs may connect to the power grid at a so-called point of common coupling (PCC), while each VSC works under its own specific condition and application, as shown in the usual representation of Fig. 1 [2]. The same structure is also employed in some specific application scenarios, including aircraft power systems [3], shipboard power systems [4], micro grids [5], etc. As each converter is designed separately for its own load condition, the mutual coupling in practice via the grid may pose a stability concern as the grid is non-ideal in reality and presents at the point of common coupling a significant amount of impedance which is not always predictable. As a result, the stability of the system should be considered with the coupled system model in mind rather than the unrealistic though simple model where each converter is assumed to behave independently.
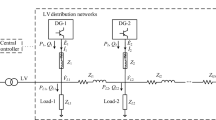
For the purpose of illustrating the effect of mutual coupling, it suffices to consider two converters under the structure shown in Fig. 2. To maintain generality of our study, the VSCs are controlled under a typical feedback configuration that contains an outer voltage loop which operates in conjunction with a sinusoidal pulse-width-modulated (SPWM) inner current loop for achieving a constant output dc voltage, as presented in Fig. 3. The two converters have been designed separately according to their respective application conditions. However, when they are connected to the non-ideal grid, their interaction may have an impact on stability.
The stability issue of grid-connected VSCs in the presence of varying grid impedance has been discussed in several prior publications. For instance, Belkhayat [6] presented an impedance-based approach to evaluate the stability of ac interfaces in the dq-frame by employing a generalized Nyquist stability criterion (GNC) based on small-signal modeling. The stability of grid-connected inverters and rectifiers has also been discussed [7–9]. Moreover, a converter’s impedance modeling has been studied in some detail [10–12]. Some preliminary studies of the effect of grid impedance on grid-connected interacting converters have been reported in [13–15]. Furthermore, some bifurcation phenomena have been observed and reported in some earlier studies [16–18].
In this paper, the important issue of the effect of interaction between the grid-connected converters under non-ideal power grid conditions is addressed, which is largely unexplored despite its practical importance. The study will probe into the key control parameters and examine how variation of these parameters alters the stability regions under the effect of converters’ interaction. Specifically, we focus on the loss of stability corresponding to emergence of a low-frequency oscillation as commonly studied under the broad class of Hopf-type bifurcation phenomena [19]. We show that the bifurcation boundaries (stability regions from an engineering viewpoint) generally shrink when converters interact via the non-ideal grid. In other words, analysis assuming independent (uncoupled) converters under ideal grid condition therefore provides over-optimistic stability prediction. In Sect. 2, we take a quick tour of the instability phenomenon arising from converters’ interaction. In Sect. 3, a detailed stability assessment employing an impedance-based approach is presented. Finally, in Sect. 4, we present our results in a design-oriented format that reveals the way in which stability would be affected by variation of selected parameters, and hence facilitates the choice of parameters for stable operation [20].
2 A glimpse at the instability
We begin by taking a quick glimpse at the way in which a voltage-source converter loses stability. The circuit of Fig. 2 is studied in full circuit implementation using MATLAB. The values of the circuit components used in the simulation are summarized in Tables 1, 2 and 3. Converters 1 and 2 employ the same control method which is described in Fig. 3.
Figure 4a shows stable operation of the two converters with different load conditions when separately connected to the same non-ideal grids with impedance L g = 1.2 mH. Thus, the converters are stable when analyzed separately. However, when the converters are connected at the same time to the non-ideal grid having the same impedance at the point of common coupling (PCC), as shown in Fig. 2, the converters’ output voltages and input currents have manifested low-frequency osci.
Figure 4b The dc voltage Udc of both converters oscillate at 255 Hz around the regulated level, while all converters’ parameters have remained the same as in the case of separate uncoupled operation.
Thus, it can be inferred that the converters could interact with each other and lose stability via a Hopf-type bifurcation when the values of parameters are selected beyond a specific region in the parameter space (referred to as stability region here).
3 Analysis
For an individual grid-connected VSC, control models and their closed-loop stability analysis have been studied [7], employing techniques like root locus analysis and Bode diagrams. Moreover, the state-space approach is also used to determine stability in the time domain [15]. For grid-connected converters, prior studies [6, 21] have pointed out that the impedance-based approach is more advantageous and flexible. For the case of the grid-connected system under study, the impedance-based analysis is highly suitable, as will be demonstrated in the subsequent subsections.
3.1 Basic system model: the uncoupled case
Following the formulation of Sun [22], the three-phase VSC can be represented by an averaged model in the dq rotating coordinate. Since converters 1 and 2 share the same model, we provide, for brevity, the equations for converter 1 as follows:
where subscript 1 denotes converter 1 (likewise, subscript 2 denotes converter 2 in the subsequent analysis); ω l = 2πf l ; d1d = u1d/udc1 and d1q = u1q/udc1 are the duty cycles; i1d and i1q are the input currents of converter 1 in the dq-frame; u gd and u gq are the voltages at the point of common coupling (PCC); u1d and u1q are the leg voltages in the dq-frame; and io1 is the load current. For simplicity, we ignore the inductor resistance r in the following analysis. From (1), we can obtain the small-signal representation via the usual linearization procedure, i.e.,
where D1d, D1q, I1d, I1q and Udc1 are the system’s steady-state values which are given by
Omitting the standard small-signal derivation, the state-space representation of the closed-loop system can be obtained as
where
and
For brevity of presentation, we define
The impedance function of the closed loop system can be written as
Therefore, the characteristic polynomial that determines the stability of the closed loop system can be found as
Thus, we can assess the stability of the system by inspecting the roots of Φ CL (s) = 0, i.e., eigenvalues of T(s). Stability requires that all eigenvalues have negative real parts. Putting the parameter values in (8), we can compute the eigenvalues as given in Table 4, which indicate stable operation of the uncoupled converters.
3.2 Analysis of the interacting converters
The foregoing subsection derives the conventional converter’s closed-loop model and assesses the stability of the converters when working independently (uncoupled). In this subsection, the converters are connected to the power grid at a common coupling point and thus interact with each other. As the two converters have identical control loops, from (7), we can derive the converters’ impedance as
Combining (9) and I o = U dc /R L , we obtain the input admittance of each converter as seen at the coupling point, i.e.,
where Y VSCk (k = 1, 2) is the converter’s input admittance and Y(s) is the total input admittance of the two converters.
In a likewise manner, the grid impedance can be found from
where
Thus, the system’s impedance can be considered in the usual Thevenin form, as shown in Fig. 5.
Based on this small-signal model, the current I s from power grid to the coupled converters is
Since the converters are stable when operating independently, both U s and Y(s) are stable and the stability of the connected system can be assessed by applying Nyquist criterion [23] to (Fig. 6)
The Nyquist plot of det(I + Y(s)Z s ), as given in Fig. 7, shows encirclement of the origin which asserts that the system is unstable. Numerical calculations of the poles of the closed-loop system also indicate unstable operation, as shown in Table 5. This result is in full agreement with the simulations presented earlier.
For a general system with multi-converters connected to a non-ideal power grid at the same PCC as shown in Fig. 1, we can track the trajectory to determine the overall system’s stability. The total input admittance of the connected system is Y VSC = YVSC1 + YVSC2 + YVSC3 + … + Y VSCn , and the impedance in dq-frame could be obtained as shown in Fig. 8. The stability could be assessed by examining the root locus of det(I + Y VSC Z s ).
The above analysis clearly exposes that the interacting converters can be unstable while the individual separately operated converters are stable.
4 Stability regions in design-oriented forms
In the foregoing analysis, the system’s stability has been determined precisely using the interface impedance. However, for engineering design purposes, it is more important to identify the system parameters and their variation trends that have significant impact on the stable region of operation [20, 24]. In this section, we derive stability boundaries using the foregoing analysis and present them in design-oriented forms. Results from simulations of the actual switching circuits will also be presented for comparison and verification.
Relevant to our present study is the region of stable operation bounded by the bifurcation boundary corresponding to the loss of stability via a Hopf-type bifurcation (practically known as low-frequency oscillation). For the system of two converters connected to a non-ideal power grid, we focus on the following parameters:
-
1)
the grid impedance L g ,
-
2)
the dc gains of the two converters’ voltage loop kvp1, kvp2,
-
3)
the converters’ load resistance RL1, RL2.
Moreover, for the purpose of comparison, the stability regions of converters coupled via the power grid and those of the independently operating (uncoupled) converters are presented. Our results are generated from simulations of the complete switching model which provides viable verification of the actual physical system.
In the sequel, we will present a series of design-oriented stability charts which are computed from the analysis of Sect. 3 and also from full circuit simulations. Each chart contains two sets of stability boundaries, shown in red and blue, corresponding to two specific parameter values as labelled in the chart. In each chart, for the red or blue set of boundaries, the parameter plane is divided into regions I, II and III.
-
Region I (stable) is the parameter region where the system is stable for both cases of independently operated converters and grid-coupled converters.
-
Region II (intermediate) is the parameter region where the independently operated converters are stable, but the system of grid-coupled converters is unstable.
-
Region III (unstable) is the parameter region where the system is unstable for both cases of independently operated converters and grid-coupled converters
Thus, the boundary separating regions I and II is the bifurcation boundary or stability threshold for the system of coupled converters, and the boundary separating regions II and III is the bifurcation boundary for the independently operated converter. In each chart, analytically calculated stability boundaries are plotted in asterisk (*), and the corresponding full circuit simulated boundaries are shown in solid curves.
The dc gains of voltage loop kvp1, kvp2 are the key parameters that affect stability with respect to Hopf bifurcation. Since the inner current loop gain is usually chosen to be sufficiently high to ensure that the current tracks the reference closely, we will ignore the inner loop gain in our study. For the system of converters connected at the same PCC, the stability regions in the kvp1–kvp2 plane is shown in Fig. 9, for both the uncoupled and coupled systems for different values of dc loads and grid impedance. These charts reveal how variation of these parameters would affect the stability regions, and specifically we see that the stable operating regions are reduced when either dc load current, line impedance or dc link capacitor is increased.
Stability boundaries on the 2-dim plane of dc gains, i.e., kvp1 versus kvp2. Points (*) are calculated from analysis of Sect. 3, and solid curves are from full circuit simulations
The dc load resistance of the converters can affect stability, as shown in the design-oriented charts of Fig. 10. From the charts presented in Fig. 10, when one converter is more heavily loaded, the system moves closer to the boundary of instability. Moreover, we observe that the region of stability shrinks when the converters are coupled via the on-ideal grid.
Stability boundaries on the 2-dim plane of load resistances, i.e., RL1 versus RL2. Points (*) are calculated from analysis of Sect. 3, and solid curves are from full circuit simulations
From the charts presented above, we see that the analytically computed boundary points are in perfect agreement with the full-circuit simulated results. The effects of different parameters on the overall system stability can be summarized qualitatively in Table 6. Specifically, the system would alter the stability margin when parameters vary. In the table, the ‘‘ + ’’ and ‘‘−’’ signs indicate increasing and decreasing values of the parameters, respectively. Correspondingly, the sign ‘‘↑’’ means enlarging the overall system stability margin, whereas ‘‘↓’’ represents reducing the stability margin. For instance, when the load decreases (−), the overall system stability region shrinks (↓), and vice versa.
5 Conclusion
Power converters connected to a non-ideal power grid are studied in this paper. The emphasis is on the mutual interaction of two or more converters via the grid and how such interaction may cause instability of the overall system. The study is important as converters are being increasingly deployed for applications involving power conversion functions that require interfacing with power grid which is often non-ideal. The significant impedance present in the grid poses an issue deserving attention as converters’ stability is no longer a standalone problem. Through mutual interaction, converters become more prone to instability under certain conditions. This paper points out that the overall system stability should be re-considered in the light of a more complete model that takes into account the interaction of converters connected to the grid at a common point of coupling. The analysis has been developed using the impedance approach, and stability boundaries are derived in various parameter planes. Findings reported in this paper would facilitate engineers in making design choices related to the selection of parameter values that would guarantee stability in a sufficiently wide parameter range.
References
Sanjuan S (2010) Voltage oriented control of three-phase boost PWM converters. Master Thesis, Chalmers University of Technology, Gothenburg, Sweden
Wang XF, Guerrero JM, Chen Z et al (2010) Distributed energy resources in grid interactive AC microgrids. In: Proceedings of the 2nd IEEE international symposium on power electronics for distributed generation systems (PEDG’10), 16–18 June 2010, Heifei, China, pp 806–812
Areerak KN, Bozhko SV, Asher GM et al (2012) Stability study for a hybrid ac–dc more-electric aircraft power system. IEEE Trans Aerosp Electr Syst 48(1):329–347
Ciezki JG, Ashton RW (2000) Selection and stability issues associated with a navy shipboard dc zonal electric distribution system. IEEE Trans Power Deliv 15(2):665–669
Ariyasinghe DP, Vilathgamuwa DM (2008) Stability analysis of microgrids with constant power loads. In: Proceedings of the IEEE international conference on sustainable energy technology (ICSET’08), 24–27 Nov 2008, Singapore, pp 279–284
Belkhayat M (1997) Stability criteria for ac power systems with regulated loads. Ph.D. Dissertation, Purdue University, West Lafayette, IN, USA
Sun J (2011) Impedance-based stability criterion for grid-connected inverters. IEEE Trans Power Electron 26(11):3075–3078
Burgos R, Boroyevich D, Wang F et al (2010) On the ac stability of high power factor three-phase rectifiers. In: Proceedings of the IEEE energy conversion congress and exposition (ECCE’10), 12–16 Sept 2010, Atlanta, GA, USA, pp 3075–3078
Belkhayat M, Cooley R, Abed EH (1995) Stability and dynamics of power systems with regulated converters. In: Proceedings of the IEEE international symposium on circuits and systems (ISCAS’95), vol 1, 30 Apr–3 May 1995, Seattle, WA, USA, pp 143–145
Harnefors L, Bongiorno M, Lundberg S (2007) Input-admittance calculation and shaping for controlled voltage-source converters. IEEE Trans Power Electron 54(6):3323–3334
Cespedes M, Sun J (2012) Impedance shaping of three-phase grid-parallel voltage-source converters. In: Proceedings of the 27th annual IEEE applied power electronics conference and exposition (APEC’12), 5–9 Feb 2012, Orlando, FL, USA, pp 754–760
Huang J, Corzine K, Belkhayat M (2007) Single-phase ac impedance modeling for stability of integrated power systems. In: Proceedings of the 2007 IEEE electric ship technologies symposium (ESTS’07), 21–23 May 2007, Arlington, VA, USA, pp 483–489
Chandrasekaran S, Boroyevich D, Lindner DK (1999) Input filter interactions in three phase ac–dc converters. In: Proceedings of the 30th annual IEEE power electronics specialists conference (PESC’99), vol 2, 26 June–2 July 1999, Charleston, SC, USA, pp 987–992
Wan C, Huang M, Tse CK et al (2013) Nonlinear behavior and instability in a three-phase boost rectifier connected to a nonideal power grid with an interacting load. IEEE Trans Power Electron 28(7):3255–3265
Huang M, Tse CK, Wong SC et al (2013) Low-frequency Hopf bifurcation and its effects on stability margin in three-phase PFC power supplies connected to non-ideal power grid. IEEE Trans Circ Syst I Regul Papers. doi:10.1109/TCSI.2013.2264698
Suto Z, Nagy I (2003) Analysis of nonlinear phenomena and design aspects of three-phase space-vector-modulated converters. IEEE Trans Circ Syst I: Fundam Theory Appl 50(8):1064–1071
Dai D, Li S, Ma X et al (2007) Slow-scale instability of single-stage power-factor-correction power supplies. IEEE Trans Circ Syst I Regul Papers 54(8):1724–1735
Xiong X, Tse CK, Ruan X (2013) Bifurcation analysis of standalone photovoltaic-battery hybrid power system. IEEE Trans Circ Syst I Regul Papers 60(5):1354–1365
Tse CK (2003) Complex behavior of switching power converters. CRC Press, Boca Raton, FL, USA
Tse CK, Li M (2011) Design-oriented bifurcation analysis of power electronics systems. Int J Bifurc Chaos 21(6):1523–1539
Harnefors L, Bongiorno M, Lundberg S (2007) Input-admittance calculation and shaping for controlled voltage-source converters. IEEE Trans Ind Electron 54(6):3323–3334
Sun J (2009) Small-signal methods for ac distributed power systems—a review. IEEE Trans Power Electron 24(11):2545–2554
Macfarlane AGJ, Postlethwaite I (1977) The generalized Nyquist stability criterion and multivariable root loci. Int J Control 25(1):81–127
Rodriguez E, El Aroudi A, Guinjoan F et al (2012) A ripple-based design-oriented approach for predicting fast-scale instability in DC-DC switching power supplies. IEEE Trans Circ Syst I Regul Papers 59(1):215–227
Acknowledgment
The work was supported by Hong Kong Polytechnic University Grants G-U866 and G-YJ32.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This article is published under license to BioMed Central Ltd. Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Wan, C., Huang, M., Tse, C.K. et al. Stability of interacting grid-connected power converters. J. Mod. Power Syst. Clean Energy 1, 249–257 (2013). https://doi.org/10.1007/s40565-013-0034-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40565-013-0034-y