Abstract
Large-scale wind farm integration has brought several aspects of challenges to the transient stability of power systems. This paper focuses on the research of the transient stability of power systems incorporating with wind farms by utilizing risk assessment methods. The detailed model of double fed induction generator has been established. Wind penetration variation and multiple stochastic factors of power systems have been considered. The process of transient stability risk assessment based on the Monte Carlo method has been described and a comprehensive risk indicator has been proposed. An investigation has been conducted into an improved 10-generator 39-bus system with a wind farm incorporated to verify the validity and feasibility of the risk assessment method proposed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Nowadays, low carbon emission has been an irresistible trend for the development of the world industry and economy. The exploitation and utilization of renewable sources (wind power especially) have received high-level attentions in many countries [1, 2]. With the enlargement of the scale of wind farms and the capacity of wind turbines, the influence of wind farms on power systems has always been a research focus, in which the challenge to the transient stability is extremely concerned by researchers.
As for the transient stability analysis of power systems, traditional analysis methods are carried out under the assumption that the system component parameters, operational condition, disturbance mode are deterministic. However, deterministic analysis methods make the stability analysis result too conservative and the security margin too large which could not fulfill the requirement of economical efficiency in power grids. Meanwhile, the result of deterministic analysis is binary (stable or unstable), the transient stability risk could not be quantified. In fact, the electric power sectors need to know the risk level so as to take actions to increase the system security. As a consequence, analyzing the system transient stability by utilizing risk assessment has become an indispensable research method [3].
A series of papers have already been published in the field of transient stability risk assessment in conventional power systems. Reference [4] utilized preconceived accident list to define the system transient stability risk indicators upon the concept of time margin. Reference [5] quantized the transient stability risk as an economic indicator to grid company, power plant, and customers, respectively. Reference [6] focused on combining the steady-state risk and the transient-state risk to establish a comprehensive transient stability risk indicator. However, the above papers did not involve the risk assessment of power systems incorporating with wind farms. Reference [7] studied the probabilistic stability of the power system integrated with wind farms. Reference [8] researched the impact on the transient stability brought by the number and penetration of the wind farm on the basis of [7]. Reference [9] aimed at the probability of transient stability in the power system incorporating with double fed induction generator (DIFG) and squirrel cage induction generator (SCIG). The above papers rarely analyzed the impact on system transient stability by wind power from the viewpoint of risk assessment.
Due to the problems mentioned above, this paper focuses on the risk assessment of transient stability in power systems incorporating with wind farms. The detailed model of DFIG has been established, and the risk assessment method for transient stability has been proposed. Based on the above analysis, a simulation has been done based on the Monte Carlo method on an improved 10-generator 39-bus system incorporating with a wind farm.
2 DFIG model
DFIG is a type of wind power generator which is very popular. In a DFIG, a slow wind turbine rotor is connected to a rapid generator rotor. The generator stator connects with the grid directly while the generator rotor connects with the grid through a group of back-to-back AC/DC/AC converters. The grid-side converter exchanges the power bi-directionally by a smoothing reactor and transformer to maintain the capacitor voltage on the DC bus. The rotor-side converter regulates the generator rotor speed by controlling the exciting current to realize the decoupling of the active and reactive powers of the DFIG.
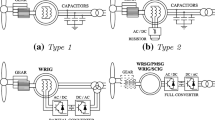
The model structure of DFIG used in this paper is shown in Fig. 1.
The main components include a windmill aerodynamic module, a drive train module, an upper-level control module, a rotor-side converter, a low voltage power logic, and the asynchronous generator electrical and mechanical equations [10]. The windmill aerodynamic module achieves the capture of the wind energy and transfers it into the kinetic energy of the wind turbine. The drive train module could be seen as a connection component between the wind turbine and the asynchronous generator. The upper-level control module achieves the maximum power point tracking and gives the reactive power signal to DFIG. The rotor-side converter transfers the upper-lever signal into an exciting voltage signal through the power and current dual closed-loop control, by which the active and reactive powers of DFIG could be decoupled.
3 Risk assessment method for power systems incorporating with wind farms
3.1 Probabilistic model
For analyzing the transient stability of a power system incorporating with wind farms, the most significant factors are the fault probabilistic model and the stochastic output power of the wind farms.
As for the probabilistic model of the line fault, References [7–9] have considered the main uncertainties, such as fault type, fault location, fault clearing time, and reclosing time. They acquired the statistical characteristics of the above uncertainties from the accumulated historical data or through the reasonable assumption [11].
As for the stochastic output power of the wind farms, many papers have considered the output features of the wind farms as the results of wind speed variation in a long-time scale [12]. However, simulations for transient stability of power systems generally take no more than 10 s, which makes the wind speed be regarded as an invariant. Therefore, this paper only considers the stochastic penetration of the wind farms.
The detailed probabilistic model of the line fault and the stochastic output power of the wind farms are described as follows.
-
1)
Fault location
The fault location could be seen as a continuous random variable. The generic approach is used to divide the line into three sections: 0 %–20 % of the line length as the near-end, 20 %–80 % as the middle section, 80 %–100 % as the tail end. The probability of fault location in these three sections is 0.1307, 0.7021 and 0.1672 correspondingly [13] and is subject to uniform distribution in each section.
-
2)
Fault clearing time
Fault clearing time is composed of the fault detection time and the action time of relay protection and switch. Generally, fault detection is assumed to be completed instantly so that the time could be ignored. However, the action time of relay protection and switch is generally assumed to be stochastic and obeys the normal distribution [8], thus the mean and variance could be obtained based on the statistical historical data. In this paper the fault clearing time is assumed to obey the normal distribution N (1.15, 0.05).
-
3)
Probabilities of successful auto-reclosing
Statistic analysis showed that only 10 % of the lightning stroke faults would lead to reclosing failures and other kind of faults would cause 50 % of the reclosing failures [14]. Reference [15] summarized the historical data of the BC Hydro Company and found that 82.51 % of faults were caused by lightning stroke. From the conditional probability equation the probability of successful auto-reclosing can be got as 0.8251 × 0.9 + (1 − 0.8251) × 0.5 = 0.83. In this paper the reclosing time is set to be 0.1 s.
-
4)
Stochastic output power of wind farm
In order to simulate the variation feature of the wind farm, this paper uses the output power probability data of an actual 900 MW wind farm (the same capacity with the original synchronous generator) [16]. The probability distribution of the wind power approximately obeys the normal distribution shown in Fig. 2. The output power of the DFIG changes from 0 MW to 900 MW during each transient simulation, and the mean value of the distribution is 398.6 MW.
3.2 Risk indicator of transient stability in a system with wind farms
The risk assessment method synthesizes the probability and the severity of the fault, and the risk indicator is applied to judge the transient stability of the system. As for the indicators of transient stability, different methods have already been proposed. Economic indicator had once been an index to evaluate the severity of the fault in early days. Although economic indicator has the advantages of clear principle and additivity, it could hardly provide a practical decision support to the operating staff because of the uncertainty of the measured power loss. Therefore, severity indicator has been a common index for the risk assessment analysis.
The risk of the whole system is given by the following equation:
where E i expresses the i-th system fault; X t and Xt+1 are the operation states before and after the fault, respectively; C is the system state after the fault; P(E i , Xt+1 | X t ) is the probability of E i with Xt+1 under the condition of X t ; I(C | E i , Xt+1) is the fault effect under the condition of E i with Xt+1; R(C | X t ) is the risk indicator.
In practical application, E i is generally in the form of discrete times and X t is a time section. Therefore, Eq. (1) is generally replaced by a reduced form as
In order to express the system operation status, this paper assesses the fault effect I by severity indicator. Two different severity indicators could be defined: power angle indicator and system voltage indicator.
-
1)
Power angle indicator
The power angle indicator Sev(St)angle could be defined by Eq. (3). It is the maximum deviation of power angle during the simulation time. If the system could remain the power angle stability, Sev(St)angle is less than 1, otherwise is equal to 1.
-
2)
System voltage indicator
The system voltage indicator Sev(St) v is defined by Eq. (4), that is the maximum ratio of two time values.
where Tlowv is the time duration when the bus voltage decreases to 0.75 p.u., Tvmax is the maximum allowable time (generally equals to 1 s). If the system could remain the voltage stability, Sev(St) v is less than 1, otherwise is greater than or equal to 1.
For each fault, the transient stability could be assessed by both the power angle risk Risk(St)angle and the voltage risk Risk(St) v . The two different risks are the multiplication values of the probability Like(St) of preconceived accident St with the fault severity indicator Sev(St)angle or Sev(St) v , so that the Eq. (2) could be written as
When the ranks of the two risk values are different, a comprehensive risk should be introduced to synthesize the power angle stability and the voltage stability. The comprehensive risk Risk(St)tra could be defined as the union of Risk(St)angle and Risk(St) v . The definition is shown as follows:
3.3 Preconceived system accident list
If all the fault conditions on each line are considered to form the accident list, a large sample size will cause massive computation and the system risk may not be assessed effectively. In fact, the fault occurrence on system line is influenced by different factors, such as the voltage level, network structure and weather situation. In practical analysis, the preconceived accident list could be selected by fault occurrence probability ranking according to the statistical historical data. The ranked top 15 faults in the historical data could be selected as the preconceived accident list to represent the fault occurrence condition [17].
3.4 Transient stability risk assessment based on Monte Carlo method
The transient stability risk assessment based on Monte Carlo method is divided into two layers: Monte Carlo state generator and deterministic transient stability simulation [18]. The flow chart of transient stability risk assessment process is shown in Fig. 3. The whole flow is divided into three steps: random sampling, transient simulation, and risk value calculation. The first step is to select samples for the four operation factors, i.e., wind farm output power, fault location, fault clearing time, and auto-reclosing status. The Monte Carlo samples are selected by sampling according to their probabilities of occurrence. The next step is the transient simulation that analyzes the system operation status sampled in the first step. The final step is to calculate the transient risk value based on the transient simulation with considering all the stochastic factors in power systems.
4 Simulation study
4.1 Simulation system description
The example system is a 10-generator 39-bus system with a wind farm incorporated. The single line diagram of the system is shown in Fig. 4. The detailed system data could be found in [19]. The original synchronous generator on bus 39 with active output power of 900 MW is replaced by a DFIG with the capacity of 900 MW. A compensating capacitor is installed to ensure the power factor of the DFIG to be 1.0 in the steady state. As described in Sect. 3.1, the active output power of the DFIG may vary from 0 MW to 900 MW. For the risk assessment, once the active output power of the DFIG is selected, the active output power of the other synchronous generators will be adjusted accordingly, and then the system power flow calculation is performed to obtain the system steady state.
The preconceived accident list is shown in Table 1 [19]. The first column represents the fault number, the second column is the fault line St, and the third column is the probability of the fault occurrence which is the value of Like(St).
4.2 Risk calculation based on preconceived accident list
Ten thousand stochastic samples are created by the Monte Carlo sampling and the transient stability simulation time in the second layer is 5 s. During each sampling, the severity indicators of power angle and voltage for a certain fault in the preconceived accident list will be calculated. After ten thousand samplings, the average value of severity indicators for each occasion will be got as Sev(St)angle and Sev(St) v . Taking the severity indicators and the corresponding Like(St) (the fault probability shown in Table 1) into Eqs. (5) and (6), the final risk Risk(St)angle and Risk(St) v of the 15 preconceived faults would be calculated. The values of Risk(St)angle, Risk(St) v and Risk(St)tra are shown in Table 2.
It could be seen from Table 2 that for the modified 10-generator 39-bus system, the power angle stability is much more serious than the voltage stability since the system has an abundant reactive power support. More attention should be paid to the power angle stability when designing controllers to enhance the system transient stability.
4.3 Transient stability risk assessment of the system with and without wind farm
In the original 10-generator 39-bus system the generator on bus 39 is a synchronous generator with active output power of 900 MW. The transient stability risk assessment of the original system is also performed as above. Moreover, the transient stability risk assessment under another operation state of the original system is also performed, in which the active output power of the synchronous generator on bus 39 is set to be 398.6 MW, that is the average value of the wind power probability distribution shown in Fig. 2. Comparing the risk assessment results of the 10-generator 39-bus system with and without wind farm, the comprehensive risks are shown in Fig. 5, where SG stands for synchronous generator.
From Fig. 5, it could be seen that the transient stability risk of most preconceived accidents decreases when the wind farm is integrated. Replacing the DFIG by a 900 MW synchronous generator rather than a 398.6 MW one, the system is much more stable. However, compare the risk values with and without the wind farm, there is a dramatic increase in the risk on both line 1–39 (fault number 3) and 9–39 (fault number 5) which are near the grid-connected point of the wind farm. This is because the fault near the wind farm will cause a significant drop of the active power of the wind farm and at the same time an increase of the reactive power absorption by the wind farm. Figures 6 and 7 illustrate the performance of the active and reactive output powers of the wind farm with a three-phase fault (lasts 0.2 s) at two different locations: line 9–39 (near the wind farm) and line 21–22 (far from the wind farm).
It can be seen from the two figures that when the fault is located near the wind farm (line 9–39), the active output power is significantly reduced. Meanwhile, large amount of reactive power is absorbed by the wind farm, which will cause the voltage deteriorated. All these factors will cause the transient stability risk increased when the fault is located near the wind farm.
5 Conclusion
The influence of large-scale wind farm integration on system transient stability has become a big issue which is urgently to be concerned. Deterministic analysis method generally neglects the uncertainties in real system. On the basis of this, this paper focuses on the risk assessment of transient stability in power systems incorporating with wind farms. The detailed model of DFIG has been established, the uncertainties of line fault and wind farm output power have been considered, and a system comprehensive risk indicator has been proposed. The transient stability risk assessment of a 10-generator 39-bus system incorporating with a wind farm has been investigated based on the Monte Carlo method. The results show that the risk of the line near the grid-connected point of the wind farm will increase and the risk of the line far from the point will slightly decrease.
References
Li XR, Hui JH, Qian J (2009) Impact of wind power generation on load modeling in distribution network. Autom Electr Power Syst 33(13):89–94 (in Chinese)
Lei YZ, Wang WS, Yin YH (2002) Wind power penetration limit calculation based on chance constrained programming. Proc CSEE 22(5):33–36 (in Chinese)
Thapa S, Karki R, Billinton R (2011) Evaluation of wind power commitment risk in system operation. In: Proceedings of the 2011 IEEE electrical power and energy conference (EPEC’11), Winnipeg, Canada, 3–5 Oct 2011, pp 284–289
Wang SX, Zhang BM, Guo Q (2005) Transient security risk assessment of global power system based on time margin. Proc CSEE 25(15):51–55 (in Chinese)
Wang W, Mao JA, Zhang LZ et al (2009) Risk assessment of power system transient security under market condition. Proc CSEE 29(1):68–73 (in Chinese)
Liu XD, Jiang QY, Cao YJ et al (2009) Transient security risk assessment of power system based on risk theory and fuzzy reasoning. Electr Power Autom Equip 29(2):15–20 (in Chinese)
Faried SD, Billinton R, Aboreshaid S (2009) Probabilistic evaluation of transient stability of a wind farm. IEEE Trans Energy Convers 24(3):733–739
Faried SD, Billinton R, Aboreshaid S (2010) Probabilistic evaluation of transient stability of a power system incorporating wind farms. IET Renew Power Gener 4(4):299–307
Meegahapola L, Flynn D (2010) Impact on transient and frequency stability for a power system at very high wind penetration. In: Proceedings of the 2010 Power and Energy Society General Meeting, Minneapolis, MN, USA, 25–29 Jul 2010, p 8
Rezaei E, Ebrahimi M (2012) Dynamic model and control of DFIG wind energy systems based on power transfer matrix. IEEE Trans Power Deliv 27(3):1485–1493
Zhao SS, Zhong WZ, Zhang DX et al (2009) A transient voltage instability risk assessment method and its application. Autom Electr Power Syst 33(19):1–4 (in Chinese)
Najafi HR, Robinson F, Dastyar F et al (2008) Transient stability evaluation of wind farm implemented with induction generators. In: Proceedings of the 43rd International Universities Power Engineering Conference (UPEC’08), Padua, Italy, 1–4 Sept 2008, p 5
Allan R, Billinton R (2000) Probabilistic assessment of power systems. Proc IEEE 88(2):140–162
Liu WY, Lu JP (2005) Monte Carlo method for probabilistic transient stability assessment. Proc CSEE 25(10):18–23 (in Chinese)
Vaahedi E, Li W, Chia T et al (2000) Large scale probabilistic transient stability assessment using BC Hydro’s on-line tool. IEEE Trans Power Syst 15(2):661–667
Transnet BW GmbH. http://www.enbw-transportnetze.de/ kennzahlen/erneuerbare-energien/windeinspeisung/
Wu D (2012) A method of energy storage’s location and capacity optimization based on transient stability risk assessment. Dissertation, Huazhong University of Science & Technology, Wuhan, China (in Chinese)
Timko KJ, Bose A, Anderson PM (1983) Monte Carlo simulation of power system stability. IEEE Trans Power Appar Syst 102(10):3453–3459
Padiyar KR (2002) Power system dynamics stability and control, 2nd edn. BS Publications, Hyderabad
Acknowledgments
This work is supported by State Grid Corporation of China, Major Projects on Planning and Operation Control of Large Scale Grid (SGCC-MPLG026-2012), and National HI-Tech R&D Program of China (2011AA05A112).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This article is published under license to BioMed Central Ltd.Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Miao, L., Fang, J., Wen, J. et al. Transient stability risk assessment of power systems incorporating wind farms. J. Mod. Power Syst. Clean Energy 1, 134–141 (2013). https://doi.org/10.1007/s40565-013-0022-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40565-013-0022-2