Seismic analysis of high-speed railway irregular bridge–track system considering V-shaped canyon effect

Abstract

To explore the effect of canyon topography on the seismic response of railway irregular bridge–track system that crosses a V-shaped canyon, seismic ground motions of the horizontal site and V-shaped canyon site were simulated through theoretical analysis with 12 earthquake records selected from the Pacific Earthquake Engineering Research Center (PEER) Strong Ground Motion Database matching the site condition of the bridge. Nonlinear seismic response analyses of an existing 11-span irregular simply supported railway bridge–track system were performed under the simulated spatially varying ground motions. The effects of the V-shaped canyon topography on the peak ground acceleration at bridge foundations and seismic responses of the bridge–track system were analyzed. Comparisons between the results of horizontal and V-shaped canyon sites show that the top relative displacement between adjacent piers at the junction of the incident side and the back side of the V-shaped site is almost two times that of the horizontal site, which also determines the seismic response of the fastener. The maximum displacement of the fastener occurs in the V-shaped canyon site and is 1.4 times larger than that in the horizontal site. Neglecting the effect of V-shaped canyon leads to the inappropriate assessment of the maximum seismic response of the irregular high-speed railway bridge–track system. Moreover, engineers should focus on the girder end to the left or right of the two fasteners within the distance of track seismic damage.

Introduction

With the development of western regions in China, railway construction is gradually extending to the complex topography and high seismic intensity areas of the southwest mountainous area, and the risk of high-speed railways suffering from earthquakes in the mountainous area is also increasing [1, 2]. Moreover, the seismic analysis of the railway bridge–track system built on the mountainous topography needs to consider two negative effects: (i) the dynamic characteristics and seismic responses of adjacent spans of irregular bridges (such as different pier heights, different bridge types, etc.) are different due to various topographies [3, 4]; (ii) the spatial variability effect of ground motion distribution caused by local site and irregular topography leads to different parameters of ground motion excitation at different pier locations [5,6,7].

However, the current Code for Seismic Design of Railway [8] in China rarely consider the effect of mountainous topography on seismic intensity, peak ground acceleration (PGA), peak ground velocity (PGV), etc. This may underestimate the amplification effect and spatial variability of ground motion in complex topographies, and cause potential danger during the construction of high-speed railway (HSR) bridge in mountainous topography [9, 10]. According to the actual strong earthquake observation and earthquake damage survey of the United States Pacoima dam in 1971 [11], Taiwan Hualian earthquake in 1992 [12], and Wenchuan earthquake in 2008 [13], it is found that there is obvious spatial variability of ground motion at different positions on both sides of the valley or canyon. To reveal the mechanism of the canyon topography effect, many scholars have carried out analytical research and numerical simulation on the scattering and diffraction of seismic waves by the canyon topography [14]. The theoretical analysis method mainly refers to the wave function expansion method [15, 16]. Numerical methods include finite difference method [17], spectral element method [9], finite element method [18], boundary element method [19], and hybrid method [20]. Using the theoretical analysis method (wave function expansion method), Gao [21] reported that the peak acceleration recorded at SC1 was more than 2.5 times that at the SC4 of the Feitsui canyon (V-shape). Liu and Feng [22] used the theoretical analysis method to discuss the seismic wave scattering of P waves in the case of V-shaped canyon topography. Li [23] studied the scattering of the semi-circular hills on cylindrical shear-horizontal (SH) wave based on the theoretical analysis method. It was found that the ground motions in the example site exhibit spatial variability because of the canyon topography. Therefore, excluding the spatial variability of ground motions in the canyon topography may lead to improper estimation of the seismic responses of the high-speed railway bridge–track system, which highlights the great importance of analyzing the effect of canyon topography on the seismic performance of the bridges located in the V-shaped canyon.

The effects of many aspects of spatially varying ground motions, including the wave passage, coherency loss, local site effect, etc., on the seismic responses and fragilities of highway bridges, have been extensively investigated [10, 24]. However, for railway bridges, the higher the rigidity of the piers, the lower the reinforcement ratio [4, 25]. In addition, the railway bridge–track system has a complex seismic response, and the track structure is prone to damage [26, 27]. The higher requirements for the running safety of the upper track structure require a more detailed analysis of the track damage on the railway bridge [28,29,30]. Wei et al. [31, 32] used consistent seismic inputs to study the seismic fragility of the CRTS-II track system under different ground motion angles and seismic isolation bearings. Some other researchers [4, 33] carried out nonlinear dynamic analysis studies on the CRTS-II track system on the irregular bridge based on the uniform seismic input. They found that the track structure on the bridges with unequal height piers is more prone to earthquake damage than the bridges with equal height piers. Moreover, the relative deformation is significant at the joints of the simply supported beam ends, where the track structure is most likely to be damaged. However, these studies used uniform seismic inputs and have not considered topography effects [34, 35], and currently there are few studies on the seismic damage of the track structure on the bridge under the canyon topography, although the track structure on railway bridges is very important and its damage needs to be considered. Therefore, it is necessary to study the impact of spatially varying ground motions caused by topography effects on the seismic damage of ballastless track on irregular simply supported beam bridges in mountainous topography.

In order to investigate the effect of canyon topography on the seismic response of high-speed railway bridge–track system, this paper uses an existing 11-span simply supported railway bridge in a V-shape canyon as a prototype to establish the finite element model in OpenSees. Matching the site condition of the bridge with 12 earthquake records from the PEER Strong Ground Motion Database, the seismic ground motions of the horizontal site and V-shaped canyon site are simulated through theoretical analysis. Then, the seismic responses of the example bridge under the simulated ground motions from different topography models are analyzed to reveal the effect of V-shaped canyon topography on the seismic performance of irregular high-speed railway bridge–track system.

Modeling of a detailed high-speed bridge–track system

General information of high-speed bridge–track system

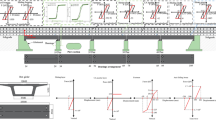
The railway simply supported girder bridge is located on the V-shaped canyon section in a western mountainous area of China. The depth of the V-shaped canyon is 81.3 m, and the bridge is composed of 11-span simply supported girders, with a total length of 357.5 m, as shown in Fig. 1a. The single-span length of the girder is 32.4 m. The arrangement of bearings is given in Fig. 1b, with 4 bearings on each pier including the longitudinal movable bearing, the transverse movable bearing, the bidirectional movable bearing, and the fixed bearing. The track structure on the bridge is a CRTS-I double-block ballastless track, which is mainly composed of groove, geotextile, rails, fasteners, track plates, and base plates, as shown in Fig. 1c. The main function of the groove is to limit the displacement of the track structure.

Fig. 1

Layout of 11-span simply supported bridge–track system in the high-speed railway: a simply supported bridge–track system; b arrangement of bearings; c CRTS-I double-block ballastless track

Finite element model of the high-speed bridge–track system

In this paper, a finite element model of the bridge–track system is established using the OpenSees. The mechanical diagram is shown in Fig. 2. The main girder, track plate, and base plate are assumed to be elastic and the specific values of their properties are shown in Table 1.

Fig. 2

Mechanical diagram of the bridge–track system

Table 1 Parameters of each component

The type of the selected bearings is KZQZ-5500, an isolate bearing, and a bilinear model is used to describe its nonlinearity. The stiffness of the movable bearing before yielding can be expressed as [36]

$$k = \mu W/D_{{\text{y}}} ,$$

(1)

where $\mu$ is coefficient of friction, taken as 0.06; $W$ is the vertical load of the superstructure; $D_{{\text{y}}}$ is yield displacement with a value range of 0.002–0.005 m, and 0.005 m is used in this article.

The stiffness of the bearing after yielding can be expressed as [37]

$$k_{\text{h}} = F/R_{{{\text{eq}}}} ,$$

(2)

where $F$ is the design vertical bearing capacity; $R_{{{\text{eq}}}}$ is the equivalent radius of curvature of the bearing, which is 3.84 m. The bearing adopted is a double spherical seismic isolation bearing with a vertical bearing capacity of 5500 kN [37], the bearing design displacement is 300 mm, the restoring force model is bilinear [38], the sliding force of the movable bearing is 183.78 kN, and the stiffness of the movable bearing before and after yield is 36.7 and 14.3 kN/mm, respectively. The design horizontal load of the fixed bearing is taken as 10% of the vertical bearing capacity, which is 550 kN. All bearings are simulated by zeroLength elements [39].

To simulate the post-earthquake damage of bridges and track structures, the bridge piers and rails adopt nonlinear beam-column elements (nonlinearBeamColumn). The length of the pier element is 4 m. The reinforcement of the pier is simulated using the Steel01 constitutive model (Fig. 2) in OpenSees. The yield strength of the steel is 400 kN and the yield ratio is 0.1. The concrete of the pier adopts the Concrete02 constitutive model (Fig. 2) for simulation. The peak compressive stress is 33.5 Mpa and the peak strain is 0.0033. The length of the rail unit is 0.6 m, and the Steel01 constitutive model is also used for simulation. The geotextile and groove are simplified into one unit; that is, the relative displacement is not considered and is simulated by zero-length elements. The force–displacement mechanical model is simplified into two sections. In the first section, the geotextile first bears the load, the yield displacement is 0.5 mm, and the yield force is 149.55 kN. The second section is for the groove to bear the load, the yield displacement is 1 mm, and the yield force is 239.55 kN [40].

In the girder region, the base plate is poured on the foundation of the girder. The fastener type of the CRTS-I double-block ballastless track structure is WJ-8. The transverse stiffness and longitudinal stiffness of the fastener are taken as 37.5 and 7.5 kN/mm, respectively [31]. The parameter information is summarized in Table 2, and the resilience model is shown in Fig. 2.

Table 2 Summary of zero-length unit parameters

Analytical simulation of seismic wave propagation in V-shaped canyon

Ground motion selection

Considering far-field earthquakes, the ground motion with a source distance more than 100 km is selected. The intensity of selected ground motions is scaled to the seismic fortification intensity of the HSR bridge, corresponding to 8-degree design earthquake with the PGA of 0.3g (0.1g for frequent earthquake) [8]. The site is located on the medium hard soil associated with the shear velocity of 250–500 m/s, represented as the characteristic period of 0.4 s in the design spectrum. Considering the seismic energy input, the effective time duration of selected ground motion records should be more than 10 times the fundamental periods of bridge–track system models. To obtain more reliable results, at least seven seismic records should be selected for seismic analysis of the structure according to the Chinese code [38]. In this paper, 12 ground motion records from the PEER Strong Ground Motion Database [41] are selected, as shown in Table 3, R_rup is the closest distance to the rupture surface. The mean spectra acceleration (S_a) of selected ground motions is in basic agreement with the design S_a, as shown in Fig. 3.

Table 3 Selected ground motion records

Fig. 3

Design spectrum and spectra of the selected records

Analytical solution of ground motion for V-shaped canyon

To accurately evaluate the canyon seismic effect, this paper adopts the seismic wave analytical model of the V-shaped canyon proposed by Tsaur [42]. The SH waves are used as excitations of the model and the displacement is in the y-direction (Fig. 1). Since this paper only considers the impact of transverse (y-direction) ground motion on the seismic damage of the irregular HSR bridge–track system under the topography effect, only the SH wave is selected as the ground motion input model.

The regional division idea is used to divide the V-shaped canyon into two parts, as shown in Fig. 4. The origin of global coordinate systems $\left( {x,y} \right)$ and $\left( {r,\theta } \right)$ is set at the center of the canyon top, while the origin of local coordinate systems $(x_{1} ,y_{1} )$ and $(r_{1} ,\theta_{1}$) is at the canyon bottom. The model medium is assumed to be elastic, isotropic, and homogeneous, in which only scattered sites exist in region ②, and there are both scattered and free sites in region ①. $\alpha$ is the incident angle of SH wave, a is the half-width of the canyon, d is the depth of the canyon, and $c = 400 {\text{m}}/{\text{s}}$ is the velocity of shear wave.

Fig. 4

Geometric layout of the V-shaped canyon

Region ① and region ② should satisfy the wave equation:

$$\nabla^{2} u_{j} + k^{2} u_{j} = 0,\,\,\,\, j = 1,2,$$

(3)

where $\nabla^{2}$ is the two-dimensional Laplacian operator; $k = \omega /c$ is the shear wavenumber, and $\omega$ is circular frequency; u_j is the displacement of region j, where j = 1 and 2, representing the total displacement sites in regions ① and ②, respectively.

The displacement and stress continuity conditions of region ① and region ② and the condition of zero stress on the surface of the canyon should satisfy

$$\tau_{\theta z}^{1} = \frac{\mu }{r}\frac{{\partial u_{1} \left( {r,\theta } \right)}}{\partial \theta } = 0,\,\,\,\,\,\theta = \pm \frac{\pi }{2}, r > a,$$

(4)

$$\tau_{{\theta_{1} z}}^{2} = \frac{\mu }{{r_{1} }}\frac{{\partial u_{2} \left( {r_{1} , \theta_{1} } \right)}}{{\partial \theta_{1} }} = 0,\,\,\,\,\,\theta_{1} = - \beta_{1} ,\beta_{2} ,$$

(5)

where $\tau_{\theta z}^{1}$ and $\tau_{{\theta_{1} z}}^{2}$ are the stress on the horizontal ground surface and the canyon surface, respectively; $\beta_{1} {\text{ and }}\beta_{2}$ are angels as shown in Fig. 4. For the region ①, the wave site can be divided into two parts: the free site caused by the incident SH wave when there is no V-shaped canyon and the scattered site caused by the V-shaped canyon. The total free site displacement of region ① can be obtained by superposing the incident wave and the reflected wave:

$$u_{{\text{f}}} \left( {r,\theta } \right) = \exp \left[ {{\text{i}}kr{\text{cos}}\left( {\theta + \alpha } \right)} \right] + \exp \left[ { - {\text{i}}kr{\text{cos}}\left( {\theta - \alpha } \right)} \right],$$

(6)

where i is the imaginary unit and equal to the square root of −1.

Using Eqs. (3)-(6), the wave equation of region ① and region ② in the plane wave site can be obtained by the wave function expansion method:

$$\begin{aligned} u_{{\text{f}}} \left( {r,\theta } \right) = & 2\sum\nolimits_{n = 0}^{\infty } {\varepsilon_{n} \left( { - 1} \right)^{n} J_{2n} \left( {kr} \right)\cos \left( {2n\alpha } \right)\cos \left( {2n\theta } \right)} \\& - 4\text{i}\sum\nolimits_{n = 0}^{\infty } {\left( { - 1} \right)^{n} J_{2n + 1} \left( {kr} \right)\sin \left[ {\left( {2n + 1)\alpha } \right)} \right] \times \sin \left[ {\left( {2n + 1)\theta } \right)} \right]} \\ \end{aligned},$$

(7)

$$\begin{aligned} u_{{{\text{s0}}}} \left( {r,\theta } \right) = & - 2\sum\nolimits_{n = 0}^{\infty } {\varepsilon_{n} \left( { - 1} \right)^{n} \frac{{J_{2n}^{^{\prime}} \left( {ka} \right)}}{{H_{2n}^{{\left( 2 \right)^{^{\prime}} }} \left( {ka} \right)}}H_{2n}^{\left( 2 \right)} \left( {kr} \right) \times \cos \left( {2n\alpha } \right)\cos \left( {2n\theta } \right)} \\& + 4\text{i}\sum\nolimits_{n = 0}^{\infty } {\left( { - 1} \right)^{n} \frac{{J_{2n + 1}^{^{\prime}} \left( {ka} \right)}}{{H_{2n + 1}^{{\left( 2 \right)^{^{\prime}} }} \left( {ka} \right)}}H_{2n + 1}^{\left( 2 \right)} \left( {kr} \right) \times \sin \left[ {\left( {2n + 1)\alpha } \right)} \right]\sin \left[ {\left( {2n + 1)\theta } \right)} \right],} \\ \end{aligned}$$

(8)

$$u_{{{\text{s1}}}} \left( {r,\theta } \right) = \sum\nolimits_{n = 0}^{\infty } {A_{n} \frac{{H_{2n}^{\left( 2 \right)} \left( {kr} \right)}}{{H_{2n}^{{\left( 2 \right)^{^{\prime}} }} \left( {ka} \right)}}\cos \left( {2n\theta } \right)} + \sum\nolimits_{n = 0}^{\infty } {B_{n} \frac{{H_{2n + 1}^{\left( 2 \right)} \left( {kr} \right)}}{{H_{2n + 1}^{{\left( 2 \right)^{^{\prime}} }} \left( {ka} \right)}}\sin \left[ {\left( {2n + 1)\theta } \right)} \right],}$$

(9)

$$u_{1} \left( {r,\theta } \right) = u_{{\text{f}}} \left( {r,\theta } \right) + u_{{{\text{s0}}}} \left( {r,\theta } \right) + u_{{{\text{s1}}}} \left( {r,\theta } \right),$$

(10)

$$\begin{aligned} u_{2} \left( {r,\theta } \right) = & \sum\nolimits_{n = 0}^{\infty } {\frac{{C_{n} }}{{J_{nv}^{^{\prime}} \left( {k\check{a} } \right)}}\sum\nolimits_{m = - \infty }^{\infty } {J_{nv + m} \left( {kr} \right)T_{n,m}^{{\text{C}}} \cos \left[ {\left( {nv + m} \right)\theta } \right]} } \\& - \sum\nolimits_{n = 0}^{\infty } {\frac{{C_{n} }}{{J_{nv}^{^{\prime}} \left( {k\check{a} } \right)}}\sum\nolimits_{m = - \infty }^{\infty } {J_{nv + m} \left( {kr} \right)T_{n,m}^{{\text{S}}} \sin \left[ {\left( {nv + m} \right)\theta } \right],} } \\ \end{aligned}$$

(11)

where $J_{n} \left( \cdot \right)$ and $H_{n}^{\left( 2 \right)} \left( \cdot \right)$ denotes the nth-order Bessel function of the first kind and Hankel function of the second kind, respectively; $J_{n}^{^{\prime}} \left( \cdot \right)$ and $H_{n}^{{\left( 2 \right)^{^{\prime}} }} \left( \cdot \right)$ denote the derivatives of $J_{n} \left( \cdot \right)$ and $H_{n}^{\left( 2 \right)} \left( \cdot \right)$, respectively; n and m are the truncation number of wave function expansion method, and $\check{a}= a - r_{\text{e}}$; $T_{n,m}^{{\text{C}}} = {J}_{m} \left( {kr_{{\text{e}}} } \right){\text{cos}}\left[ {m\theta_{\text{e}} - nv\beta_{1} } \right]$ and ${T}_{n,m}^{{\text{S}}} = {J}_{m} \left( {kr_{{\text{e}}} } \right){\text{cos}}\left[ {m\theta_{{\text{e}}} - nv\beta_{1} } \right]$, respectively [42]; $A_{n}$, $B_{n}$ and $C_{n}$ are undetermined coefficients; $v = \uppi /\left( {\beta_{1} + \beta_{2} } \right)$; $u_{{{\text{s0}}}} \left( {r,\theta } \right) \,{\text{and}}\, u_{{{\text{s1}}}} \left( {r,\theta } \right)$ are the displacements of scattering site in region ①. Based on Eqs. (10) and (11), the displacement of each point in the region can be obtained.

Ground motion generation of V-shaped canyon

To obtain the topographic magnification in the time domain at each pier position, the following steps are needed: Firstly, the input Fourier spectrum of the incident seismic acceleration time history can be obtained using the fast Fourier transform technique (FFT). Afterward, the corresponding Fourier spectrum of the input acceleration time history should be multiplied by the transfer functions (Eqs. 10 and 11) to obtain the response Fourier spectrum at each pier position. Finally, through the inverse fast Fourier transform (IFFT), the earthquake response in the time domain at each pier position can be obtained accordingly.

To compare the spatial variability of ground motions in the V-shaped site, an analytical solution model of the horizontal site (no topography) was established. According to Eqs. (10) and (11), the magnification of the topography of the horizontal site at each pier position is 2. Then take the selected ground motion in Sect. 3.1 as input. To clarify the influence of the V-shaped canyon topography effect, the seismic incidence angle of this article is determined to be 60°, and the influence of other incident angles will be discussed in future research.

Take record 4 as an example, the magnifications of the V canyon site at different bridge sites relative to the horizontal site are obtained as shown in Table 4 and Fig. 5. Compared with the horizontal site case, after considering the V-shaped canyon effect, the magnification of ground motion on the seismic wave incident side (A1-P4 on the left side of the canyon) is significantly greater than that on the back wave side (P5-A2 on the right side of the canyon).

Table 4 Ratio of the peak acceleration at each pier bottom in the V-shaped site to that of the horizontal site (record 4)

Fig. 5

Seismic wave amplification effect on different sites (record 4)

The comparison of the Fourier acceleration amplitude of the V-shaped site and the horizontal site under record 4 is shown in Fig. 6. There is a certain difference in the Fourier acceleration amplitude of the V-shaped canyon site and the horizontal site. Under the V-shaped site, the Fourier acceleration amplitudes of the adjacent bridge piers are quite different, which reveals that the V-shaped canyon topography can induce the spatial variability of ground motions.

Fig. 6

Comparison of seismic wave Fourier acceleration amplitudes on different sites

The acceleration time histories of the V-shaped site and the horizontal site under record 4 are compared in Fig. 7. It can be seen that there are obvious differences in the acceleration time history curves. Especially for the P5 and A2, the PGA of the horizontal site is significantly larger than that of the V-shaped site.

Fig. 7

Comparison of acceleration time histories between V-shaped site and horizontal site: a for A1 and A2; b for P4 and P5

Seismic response analysis of high-speed bridge–track system

To clarify the impact of the V-shaped canyon topography on the dynamic response of the high-speed bridge–track system, seismic dynamic responses of the bridge–track system on the V-shaped site and the horizontal site are compared. The same bridge–track system is adopted for the horizontal and the V-shaped sites. The ground motion acceleration under the V-shaped site is considered in accordance with Sect. 3.2.

Table 4 illustrates the details of the selected ground motion records, which are used for case setting for the V-shaped site and horizontal site. For example, the V-shaped site is defined as AVS1 and AVS2 under the records of earthquakes records 1 and 2, and the horizontal site is simplified to HS1 and HS2 under the records of earthquakes records 1 and 2. In the following analysis, if not specified, the displacement is relative.

Displacements of the bridge pier top and bearing

The mean transverse peak displacement response of pier tops and transverse movable bearings under 12 seismic records are shown in Figs. 8 and 9, respectively. It can be seen that the peak displacement of the pier top in the P4 is the largest for both two cases. Under the design earthquake, the mean transverse peak displacements of the P4 pier tops on the canyon site and the horizontal site are 135 mm and 124 mm, respectively. Similarly, the mean transverse peak displacements of the movable bearings on the canyon site and the horizontal site are 74 and 69 mm, respectively. With the V-shaped canyon, both the peak displacements of the bearing on P4 and P4 pier tops increase. This indicates that neglecting the effect of V-shaped canyon topography could underestimate the transverse peak displacement of the high-speed railway bridge.

Fig. 8

Mean transverse peak displacement responses of pier tops under 12 seismic records: a frequent earthquake; b design earthquake

Fig. 9

Mean transverse peak displacement responses of transverse movable bearings under 12 seismic records: a frequent earthquake; b design earthquake

The heights of P4 and P5 are similar, 75 and 73 m, respectively. But the difference in the mean transverse peak displacement of the P4 and P5 pier tops in the V-shaped site is 41 mm, while the difference in the horizontal site is 11 mm under the design earthquake. The relative displacement difference of adjacent P4 and P5 pier tops under the design earthquake of record 4 is shown in Fig. 10a. It can be seen that there are relative displacements between P4 and P5 for the case of horizontal site, indicating that irregular simple supported railway bridges produce relative displacement responses due to the nonuniform dynamic response of adjacent piers. However, the relative displacement between P4 and P5 for the case of the V-shaped canyon topography is larger than that of the horizontal site case (almost 2 times the horizontal site). As Fig. 10b shows, the input Fourier acceleration amplitudes of the ground motion at the bottom of the P4 and P5 piers are quite different due to the canyon effect. This indicates that the spatial variability of ground motion caused by topography effects further increases the relative displacement response between adjacent piers.

Fig. 10

Relative displacement and Fourier acceleration amplitude of adjacent P4 and P5 under design earthquake of record 4: a relative displacement of adjacent P4 and P5; b Fourier acceleration amplitude under V-shaped site

The hysteresis curve of the transverse movable bearing on the pier 4 under the seismic record 4 is shown in Fig. 11, where the bearing exhibits nonlinear behavior even though under frequent earthquakes. Compared with the horizontal site, the displacement and force of the transverse bearing on the P4 increase after considering the V-shaped canyon effect.

Fig. 11

Hysteresis curve of transverse movable bearing on P4 pier under seismic record 4: a frequent earthquake; b design earthquake

Fastener displacement and damage mechanism

To determine where the fastener is prone to damage, the maximum transverse displacement of the fastener in the y-direction (Fig. 1) under seismic record 4 is shown in Fig. 12. It can be seen that the fastener has the largest displacement at the end of the girder, and the displacement is smaller in the mid-span area of the girder. According to the definition in the literature [31], 2 mm is defined as slight damage for the fastener. Under the design earthquake, the fasteners in the mid-span area (P4 and P5 piers) were damaged.

Fig. 12

The transverse peak displacement of fasteners in the x direction of record 4: a frequent earthquake; b design earthquake

Figure 13 illustrates the details of fastener relative displacement (FRD), girder relative displacement (GRD) and bearing relative displacement (BRD). The peak values of FRD at the end of the girder is shown in Fig. 14. It can be seen that as the earthquake intensity increases, the FRD also increases. However, the locations of the greatest damage caused by FDR under the horizontal site and the V-shaped site are different. Moreover, under the design earthquake, the FRD in the middle area of the V-shaped canyon (P5 pier position) is greater than that of the horizontal site. Therefore, the induced V-shaped canyon topography effect has a significant influence on the damage of fasteners.

Fig. 13

Details of fastener relative displacement (FRD), girder relative displacement (GRD) and bearing relative displacement (BRD)

Fig. 14

Transverse peak values of FRD on different sites: a frequent earthquake; b design earthquake

The peak relative displacement time histories of adjacent bearings on the same pier under the design earthquake (i.e., the BRD in Fig. 13) are shown in Fig. 15. The FRD, GRD, and BRD time histories on piers P4 and P5 are shown in Fig. 16. On the P5 pier, the BRD, GRD, and FRD of the V-shaped site are 36, 32, and 14 mm, respectively, and the BRD, GRD, and FRD of the horizontal site are 28, 25, and 10 mm, respectively. That is, the maximum transverse displacement of the fasteners in the V-shaped is 1.4 times that of the horizontal site. However, it is found that the difference of BRD, GRD, and FRD between the V-shaped site and the horizontal site on the P4 pier is similar. Especially, there is a great similarity between the relative displacement time history of the fastener at the beam end, that of adjacent bearings, and that of adjacent girder ends on the same pier. It can be seen from Sect. 4.1 that the relative displacements of P4 and P5 for the case of the V-shaped canyon topography is larger than those of the horizontal site case. This makes the BRD, GRD, and FRD of the V-shaped canyon site greater than those of the horizontal site. From the discussion above, it can be concluded that the relative displacement of adjacent unequal-height piers determines the seismic responses of fasteners.

Fig. 15

Transverse peak values of BRD on different sites: a frequent earthquake; b design earthquake

Fig. 16

BRD, GRD, and FRD under design earthquake on a P4 (V-shaped site), b P5 (V-shaped site), c P4 (horizontal site), and d P5 (horizontal site)

Rail transverse residual deformation

The deformation of the track on the bridge directly affects the safety of trains. In this section we mainly compare the postearthquakes residual deformation of rails between the V-shaped canyon and the horizontal sites. The residual deformation of rails under seismic record 4 is shown in Fig. 17. It can be seen that the residual deformation of rails is not obvious in the middle area of the girder, but is significant at the two fasteners to the left or right of the girder ends (see the deformation zone in Fig. 17). Due to the topography effect of the V-shaped canyon, the residual deformation amplitudes of the rails under frequent earthquake and design earthquake are increased by 2.4 and 1.1 mm, respectively. In the P4 pier zone, the residual deformation difference between adjacent girder ends on the V-shaped canyon site is almost 2 times that on the horizontal site. Generally, the topographic effect of the V-shaped canyon will increase the residual deformation of the rail.

Fig. 17

Transverse residual deformation of rails under seismic record 4: a frequent earthquake; b design earthquake

Figures 18 and 19 show the transverse residual deformations of the pier tops and movable bearings, respectively. It can be seen that the residual deformation of the rail is similar to that of the transverse movable bearings; that is, the residual deformation of the transverse movable bearings directly affects the residual deformation of the rail. These finding indicate that the greater the residual deformation of the piers and bearings, the greater residual deformation of the rails.

Fig. 18

Transverse residual deformation of pier tops under seismic record 4: a frequent earthquake; b design earthquake

Fig. 19

Transverse residual deformation of moveable bearings under seismic record 4: a frequent earthquake; b design earthquake

Conclusion

This paper has assessed the effect of the V-shaped canyon on the seismic response of the irregular railway bridge–track system. Based on OpenSees, a refined model of existing 11-span irregular simply supported railway bridge–track system with various height piers are established. Then, 12 earthquake records are selected from the PEER Strong Ground Motion Database matching the site condition of the bridge, and the topography effect of horizontal site and V-shaped canyon site are studied through the theoretical analysis. Finally, under the 12 ground motions, the influence of the topography effect of the V-shaped canyon under the design and frequent earthquakes on the seismic damage of the irregular railway bridge–track system are analyzed. The major findings of the present study can be summarized as follows:

• (1) The ground motions in the example site exhibit spatial variability because of the canyon topography. Moreover, due to the blocking effect of the V-shaped canyon, the seismic magnification of the V-shaped canyon incident side (A1-P4) is significantly greater than that of the V-shaped canyon back side (P5-A2).

• (2) The relative displacement between adjacent piers at the junction of the incident side and the back side of the V-shaped is almost 2 times that of the horizontal site, which also determines the seismic response of the fastener. Moreover, engineers should focus on repairing the rail deformation and fastener damage in the two fastener areas to the left or right of the girder end.

• (3) After considering the topography effect, the track irregularity caused by the residual deformation of the rail is more obvious. Neglecting the effect of canyon topography leads to the inappropriate assessment of the maximum seismic response of the irregular high-speed railway bridge–track system, and adversely affects the accuracy of the train safety assessment after the earthquake.

The findings of this paper indicate that the effect of the canyon topography should be considered to appropriately estimate the seismic response of irregular railway bridge–track systems in the V-shape canyon during the seismic design and analyses of these bridges. However, it should be noted that there are still many assumptions and limitations in the current study, where only the ideal topography conditions are considered in the analytical solution models. Despite these, this study still provides some valuable suggestions and references for engineers and researchers toward the seismic analyses of irregular railway bridge–track systems in a V-shape canyon.