1 Introduction

The powerful electric locomotive has become an inevitable choice for meeting the demands of high-speed passenger and heavy-haul freight transportation in the rail transit industry. As a result, larger traction/braking powers of the locomotive are required for the traction motor and a locomotive. Meanwhile, the dynamic performance and operational reliability of the traction motor are significantly affected by the behavior of support bearings [1]. Geometrical imperfections (e.g., surface waviness) of the motor-bearing components can cause abnormal vibration and noise of the traction motor and will eventually affect its state of serviceability. Therefore, it is necessary to investigate dynamic responses of the traction motor under effect of the surface waviness and fully understand the corresponding characteristics to ensure the long-term operation stability and safety of the traction motor.

The surface waviness of bearings is usually generated from the machining process owing to the vibrations of the machine tool, which cannot be eliminated completely by the existing technology. Consequently, there have been some researchers focusing on the effect of the surface waviness on the rolling bearing or a rotor–bearing system. Generally, the surface waviness on the bearing race is represented as sinusoidal waves. Fortunately, many mature lumped parameter models of the rolling bearing [2,3,4,5] have been proposed for investigation of the bearing dynamics. Tallian and Gustafsson [6] noticed and analyzed the abnormal vibration of the rolling bearing induced by the race waviness. On the basis of the Hertz contact theory, Lynagh et al. [7] established a dynamics model of the rolling bearing, where the effect of the surface waviness on the internal radial clearance was considered and then validated by tests. Through dynamic analysis, Jang and Jeong [8] found that the centrifugal force and gyroscopic moment of the roller significantly affect the frequency responses of the rolling bearing with the surface waviness. Comparing with the time-varying displacement excitation model proposed in previous research, Liu et al. [9, 10] proposed a new model of the race waviness considering the time-varying displacement excitations and time-varying contact stiffness excitations induced by the waviness at the contact position between the roller and race. In addition, the effect of surface waviness on the time-varying friction moments of an angular contact ball bearing was analyzed in their further works [11]. Alfares et al. [12] reckoned that the inner race waviness can significantly affect the dynamic characteristics of the grinding spindle–bearing system. Yu et al. [13] investigated the dynamic responses of a rotor–bearing system with the multiple bearing faults involving the localized defect and the race waviness and addressed the time-varying wear of races.

However, some of the previous works on the surface waviness in a rolling bearing were focused on the vibration responses of the bearing or a rotor–bearing system under a uniformly distributed load, while the system vibration environment of the rotating equipment and the dynamic loads were usually ignored. The traditional modeling methods may make the research results over-idealized and simplified. Therefore, it is essential to consider the actual dynamic loads of the system. For the railway vehicle and track structure, Garg and Dukkipati [14] proposed the classical vehicle dynamics theory and analyzed the dynamic characteristics of the vehicle system. Owing to the intensified wheel–rail interaction with the increase of running speeds and axle loads, Zhai et al. [15] established a dynamics model coupling the vehicle system and track structure system via the wheel–rail interaction. In addition, Zhai et al. [16] further extended the coupled dynamics model to investigate the dynamic responses of the vehicle–track–bridge system by use of theoretical simulation and experimental tests. Xu et al. [17] focused on the effect of the system spatial variability on the vehicle–track coupled system using the method of statistics. Huang et al. [18] and Wang et al. [19], respectively, investigated the dynamic characteristics of the vehicle and the thermal characteristics of the motor bearing using SIMPACK. Based on the typical vehicle–track coupled dynamics model and a calculation method for the time-varying gear mesh stiffness, Chen et al. [20] and Liu et al. [21] proposed a planar locomotive–track coupled dynamics model considering the detailed traction power transmission path. Wang et al. [22] and Liu et al. [23] further expanded the degrees of freedom of the model in the lateral direction and established the vehicle–track spatially coupled dynamics model with gear transmissions for the high-speed train and the locomotive, respectively. These works provide a good theoretical foundation for the modeling of the locomotive–track system and are helpful to simulate the actual working conditions of the traction motor in a locomotive with intensified vibrations excited by the track random irregularity and the time-varying mesh forces from the gear transmission.

In this study, an excitation model coupling the time-varying displacement and contact stiffness is adopted for the motor bearings of a locomotive–track coupled dynamics model with traction power transmissions to investigate the effect of the surface waviness in the driving end motor bearing on the dynamic performance of the traction motor. The coupled system can provide more accurate dynamic loads (e.g., dynamic suspension forces and gear mesh forces) for traction motor subsystems. Interactions between the components of the rolling bearing (e.g., roller–race/cage/ribs contact forces and the corresponding friction forces) and the time-varying displacement and contact stiffness induced by the surface waviness are comprehensively considered in the dynamics model of the rolling bearing. Using this coupled dynamics model, more accurate vibration responses of the traction motor under the effect of the surface waviness in the motor bearing and the track random irregularity can be extracted from the dynamic simulations.

2 Dynamic modeling formulation

In the locomotive-track coupled system, the vehicle is powered by the traction motor which is hung on the bogie and supported by the wheelset. Meanwhile, the intensified wheel–rail interaction generates huge dynamic loads on the traction motor via the vibration transmission. Therefore, it may be essential to consider the system vibration environment for investigating the effect of the race waviness on the dynamic behaviors of the traction motor during the operation process of a locomotive.

2.1 Locomotive-track spatially coupled dynamics model with traction power transmissions

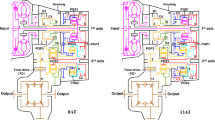
Based on the vehicle–track coupled dynamics [15], a locomotive-track spatially coupled dynamics model with traction power transmissions is proposed here. The diagram of the mechanical structure and the detailed power transmission path of the locomotive are shown in Fig. 1a, b, respectively. The car body, bogie, and wheelset are connected through the secondary and primary suspensions. The traction motor and gearcase screw together and are supported by the wheelset via the hung bearings. The hung rod of motor–gearcase is represented as a spring-damping element. The traction torque is transmitted from the traction motor to the wheel–rail interface via the gear transmission. Since the traction motor is the power source of the locomotive, its dynamic characteristics can directly affect the stability and safety of the vehicle system. In addition, the time-varying gear mesh force is the critical internal excitation for the locomotive system. The corresponding time-varying gear mesh stiffness can be calculated by an improved method proposed by Chen et al. [24].

Fig. 1
figure 1

Structure diagram of the locomotive–track spatially coupled system: a the locomotive–track system, b traction motor, and c gear transmission

Full size image

For the traction motor subsystem, the rotor and motor are connected through the motor bearings. The cylindrical roller bearing is widely adopted in the traction motor to support the rotor, reduce the friction effect, and assure the rotational precision. The gear mesh forces directly act on the pinion and significantly affect the dynamic responses of the traction motor. Besides, the system vibration induced by the intensified contact forces generated from the wheel–rail interface is transmitted to the traction motor via the components of the locomotive and the corresponding connecting elements, which is an important external excitation for the traction motor. In this section, the traction motor is represented as a rotor–bearing system. Depending on the lateral distance between the bearing and the pinion, rolling bearings with shorter/longer distances are defined as driving/non-driving end bearings. The internal excitations (e.g., the centrifugal force, unbalanced magnetic pull, rub-impact force, gravity eccentricity torque, and friction torque) induced by the dynamic eccentricity of the rotor are comprehensively considered in this model. The end view of the locomotive-track coupled dynamics model with traction power transmissions is shown in Fig. 2.

Fig. 2
figure 2

End review of the locomotive–track coupled dynamics model

Full size image

2.2 Dynamics model of the rolling bearing

Considering the dynamic loads generated or transmitted from the rotor (Wr) and motor (Wm), a dynamics model of the rolling bearing is proposed in this section. The inner and outer rings are assumed to be fixed on the rotor and motor, respectively, and the corresponding contact relationships are ignored. Therefore, the inner and outer rings of motor bearings move and rotate with the rotor and motor at the same pace, and the corresponding internal interaction forces of the rolling bearing directly act on the rotor and motor.

As shown in Fig. 3, the internal forces of the rolling bearing involve the contact forces between the roller and race as well as the cage, and the corresponding friction forces. In addition, the effect of the stiffness of the oil film at the entry and contact area on the dynamic characteristics of the rolling bearing can be ignored owing to the huge difference in magnitude [25]. Therefore, the Hertz spring stiffness is adopted to represent the interactions between the components of the rolling bearing (e.g., roller race and roller cage).

Fig. 3
figure 3

Dynamics model of the rolling bearing

Full size image

Due to the centrifugal forces of the rollers during the high-speed rotating process, the contact states between the roller and inner/outer races are different [26], and the corresponding contact forces can be, respectively, calculated as [27]

$$\left\{ {\begin{array}{*{20}l} {N_{{{\text{in}}j}} = K_{{\text{e}}} \left[ {Z_{{{\text{in}}}} \sin \sigma _{j} + X_{{{\text{in}}}} \cos \sigma _{j} - \frac{e}{2}} \right]_{ + }^{n} } \hfill \\ {N_{{{\text{ou}}j}} = N_{{{\text{in}}j}} + M_{{\text{r}}} \omega _{{{\text{o}}j}}^{{^{2} }} R_{{\text{m}}} } \hfill \\ \end{array} } \right.\;\;\;\;\;\left( {j = 1,2, \ldots ,N_{{\text{b}}} } \right),$$
(1)

where Xin and Zin are the relative displacements between the inner and outer races in longitudinal and vertical directions; σj is the angular position of the jth roller; e is the radial clearance of the bearing; the subscript ‘ + ’ indicates that the value in the brackets will be zero if it is negative; n is the load–deflection coefficients, where n = 10/9 is for cylindrical roller bearing, while n = 3/2 for ball bearing; Mr is the mass of the roller; ωoj is the circumferential speed of the jth roller; Rm is the radius of the pitch radius of the bearing; Nb is the number of rollers; Ke is the equivalent contact stiffness between the inner and outer races via the roller, which can be calculated as

$$K_{{\text{e}}} = \frac{1}{{\left[ {\left( {1/K_{{{\text{in}}}} } \right)^{n} + \left( {1/K_{{{\text{ou}}}} } \right)^{n} } \right]^{n} }},$$
(2)

where Kin and Kou are the time-varying contact stiffness between the roller and inner/outer races, respectively.

The angular position of the jth roller can be calculated as

$$\sigma _{j} = \sigma _{{\text{r}} j} + \left( {j - 1} \right)\frac{{2\uppi }}{{N_{\text{b} } }}\;\;\;\;\left( {j = 1,2, \ldots ,N_{\text{b} } } \right),$$
(3)

where σrj is the circumferential angular displacement of the jth roller.

The friction forces between the jth roller and the inner race and between the jth roller and the outer race are calculated by

$$\left\{ {\begin{array}{*{20}l} {F_{{{\text{in}}j}} = \mu _{{{\text{rr}}}} N_{{{\text{in}}j}} } \hfill \\ {F_{{{\text{ou}}j}} = \mu _{{{\text{rr}}}} N_{{{\text{ou}}j}} } \hfill \\ \end{array} } \right.\;\;\;\left( {j = 1,2, \ldots ,N_{\text{b} } } \right),$$
(4)

where μrr is the time-varying lubricant friction coefficient which varies as a function of the slipping velocity, pressure, and temperature at the contact area and can be calculated by [28]

$$\mu _{{{\text{rr}}}} = \left( {a + b\Delta V} \right)\text{e} ^{{ - c\Delta V}} + d,$$
(5)

where ΔV is the slipping velocity between the roller and race, and the computing coefficients a, b, c, and d can be deduced from the test values.

The contact force between the roller and cage (\(N_{{{\text{c}}j}}\)) and the corresponding friction forces (\(F_{{{\text{c}}j}}\)) are, respectively, calculated as follows [29]:

$$N_{{{\text{c}}j}} = K_{{{\text{rc}}}} \left( {\sigma _{{{\text{r}}j}} - \sigma _{{\text{c}}} } \right) + C_{{{\text{rc}}}} \left( {\dot{\sigma }_{{{\text{r}}j}} - \dot{\sigma }_{{\text{c}}} } \right)\;\;\;\;\;\left( {j = 1,2, \ldots ,N_{\text{b} } } \right),$$
(6)
$$F_{{{\text{c}}j}} = \mu _{{\text{c}}} N_{{{\text{c}}j}} \;\;\;\left( {j = 1,2, \ldots ,N_{\text{b} } } \right),$$
(7)

where Krc and Crc are the contact stiffness and damping between the roller and cage, respectively; μc is the corresponding friction coefficient; σc is the rotational angular displacement of the cage.

The contact forces between the roller and the ribs of inner/outer rings in the lateral direction are calculated, respectively, as

$$\left\{ {\begin{array}{*{20}l} {N_{{{\text{inr}}j}} = K_{{{\text{ry}}}} \left( {Y_{{{\text{in}}}} - Y_{{{\text{r}}j}} } \right)} \hfill \\ {N_{{{\text{our}}j}} = K_{{{\text{ry}}}} \left( {Y_{{{\text{r}}j}} - Y_{{{\text{ou}}}} } \right)} \hfill \\ \end{array} } \right.\;\;\;\;\left( {j = 1,2, \ldots ,N_{\text{b} } } \right),$$
(8)

where Kry is the contact stiffness between the roller and rib; Yin, Yrj, and You denote the lateral displacements of the inner ring, roller, and outer ring, respectively.

The resultant forces between the inner and outer rings in longitudinal, lateral, and vertical directions (x, y, and z) are, respectively, calculated by

$$\left\{ \begin{gathered} F_{{{\text{in}}x}} = \sum\limits_{{j = 1}}^{{N_{\text{b} } }} {\left( {N_{{\text{in} }j} \sin \sigma _{j} + F_{{\text{in}}j} \cos \sigma _{j} } \right)} \hfill \\ F_{{{\text{in}}y}} = \sum\limits_{{j = 1}}^{{N_{{\text{b}}} }} {N_{{{\text{in}}j}} } \hfill \\ F_{{{\text{in}}z}} = \sum\limits_{{j = 1}}^{{N_{\text{b} } }} {\left( {N_{{\text{in}}j} \cos \sigma _{j} - F_{{\text{in}}j} \sin \sigma _{j} } \right)} \hfill \\ F_{{{\text{ou}}x}} = \sum\limits_{{j = 1}}^{{N_{\text{b} } }} {\left( {N_{{\text{ou}}j} \sin \sigma _{j} + F_{{\text{ou}}j} \cos \sigma _{j} } \right)} \hfill \\ F_{{{\text{ou}}y}} = \sum\limits_{{j = 1}}^{{N_{{\text{b}}} }} {N_{{{\text{ou}}j}} } \hfill \\ F_{{{\text{ou}}z}} = \sum\limits_{{j = 1}}^{{N_{\text{b} } }} {\left( {N_{{\text{ou}}j} \cos \sigma _{j} - F_{{\text{ou}}j} \sin \sigma _{j} } \right)} \hfill \\ \end{gathered} \right..$$
(9)

Based on D’Alembert’s principle, the motion equations of the rolling bearing are formulated as follows.

Circumferential motion of the jth roller:

$$M_{{\text{r}}} R_{{\text{m}}}^{2} \ddot{\sigma }_{{{\text{r}}j}} - R_{{\text{m}}} \left( { - N_{{{\text{c}}j}} + F_{{{\text{in}}j}} - F_{{{\text{ou}}j}} - M_{{\text{r}}} g\sin \sigma _{j} } \right) = 0.$$
(10)

Self-rotation motion of the jth roller:

$$I_{{{\text{ry}}}} \ddot{\theta }_{{{\text{r}}j}} - R_{{\text{r}}} \left( {F_{{{\text{in}}j}} + F_{{{\text{ou}}j}} - F_{{{\text{c}}j}} } \right) = 0,$$
(11)

where θrj is the self-rotation angle of the jth roller.

Lateral motion of the jth roller:

$$M_{{\text{r}}} \ddot{Y}_{{{\text{r}}j}} - N_{{{\text{inr}}j}} + N_{{{\text{our}}j}} = 0.$$
(12)

Circumferential motion of cage:

$$I_{{\text{c}}} \ddot{\sigma }_{{\text{c}}} - R_{{\text{m}}} \sum\limits_{{j = 1}}^{{N_{{\text{b}}} }} {N_{{{\text{c}}j}} } = 0,$$
(13)

where Ic is the moment of inertia of the cage.

It should be noted that, considering the computational efficiency, this detailed bearing dynamics model is only used for the bearing concerned, while for other non-concerned bearings, they are simply represented as a lumped spring-mass system without relative slipping between the components of the bearing [30] or even ignored in the locomotive-track coupled system.

2.3 Excitation model of bearing surface waviness

As a typical geometrical characteristic of a distributed defect, the surface waviness can significantly change the geometrical topography of the race and further affect the contact stiffness at the contact area between the roller and race. The waviness is in the form of alternate peaks and valleys; therefore, it can be represented by a sinusoidal surface [31]. The schematic of the contact type between the roller and race with or without surface waviness is shown in Fig. 4. In this study, an excitation model [10] coupling the time-varying displacement and contact stiffness is adopted to analyze the effect of the uniform surface waviness on the motor bearing.

Fig. 4
figure 4

Schematic of the contact type between the roller and races with or without waviness

Full size image

Given the initial amplitude of the waviness Δ0, the amplitude of the uniform race waviness can be formulated as [10]

$$\varDelta {{ = }}\varDelta _{{\text{0}}} {\text{ + }}\varDelta _{{\text{w}}} \sin \left( {\frac{{2{\uppi }L_{{\text{w}}} }}{{\lambda _{{\text{w}}} }} + \sigma _{0} } \right),$$
(14)

where Δw is the maximum amplitude of the waviness; σ0 is the initial phase angle; λw is the mean wavelength; and Lw is the relative arc length of the wave at the contact angle, which can be calculated as

$$\lambda _{{\text{w}}} = \frac{{2{\uppi }}}{{N_{{\text{w}}} }},$$
(15)
$$L_{{\text{w}}} = \left\{ {\begin{array}{*{20}l} {\sigma _{{{\text{ri}}}} R_{{{\text{in}}}} } \hfill & {{\text{(inner race waviness)}}} \hfill \\ {\sigma _{{{\text{ro}}}} R_{{{\text{ou}}}} } \hfill & {{\text{(outer race waviness)}}} \hfill \\ \end{array} } \right.,$$
(16)

where Nw is the wavenumber; Rin and Rou are the radiuses of the inner and outer races, respectively; σri and σro are the relative contact angles between the roller and inner/outer races, respectively, and are given by

$$\left\{ {\begin{array}{*{20}l} {\sigma _{{{\text{ri}}}} = \sigma _{j} - \theta _{{{\text{rot}}}} } \hfill & {{\text{(inner race waviness)}}} \hfill \\ {\sigma _{{{\text{ro}}}} = \sigma _{j} - \theta _{{{\text{mot}}}} } \hfill & {{\text{(outer race waviness)}}} \hfill \\ \end{array} } \right.,$$
(17)

where θrot and θmot are the rotational and pitch angular displacements of the rotor and motor, respectively. However, θmot can be assumed to be 0 owing to the small pitch angle of the motor.

According to Eq. (14), the curvature of the wavy race can be deduced as

$$\rho _{\text{w} } = \frac{{\left| {\varDelta ^{{\prime \prime }} } \right|}}{{\left( {1 + \varDelta ^{{\prime 2}} } \right)^{{\frac{3}{2}}} }} = \frac{{\left| {\varDelta _{\text{w} } \left( {\frac{{2\uppi }}{{\lambda _{\text{w} } }}} \right)^{2} \sin \left( {\frac{{2{\uppi }L_{\text{w} } }}{{\lambda _{\text{w} } }}} \right)} \right|}}{{\left[ {1 + \varDelta _{\text{w} }^{2} \left( {\frac{{2\uppi }}{{\lambda _{{\text{w}}} }}} \right)^{2} \cos ^{2} \left( {\frac{{2{\uppi }L_{\text{w} } }}{{\lambda _{\text{w} } }}} \right)} \right]^{{\frac{3}{2}}} }}.$$
(18)

The corresponding curvature radius of the wavy race is

$$R_{{\text{w}}} = \frac{1}{{\rho _{{\text{w}}} }}.$$
(19)

Based on the Hertz contact theory, the elastic deformation between the roller and wavy race is calculated as [32]

$$\delta _{{{\text{rw}}}} = \frac{{2Q}}{{{\uppi }L_{c} }}\left[ {\frac{{1 - v_{1}^{2} }}{{E_{1} }}\left( {\ln \frac{{2R_{r} }}{{b_{{{\text{rc}}}} }} + 0.407} \right) + \frac{{1 - v_{2}^{2} }}{{E_{2} }}\left( {\ln \frac{{2R_{{\text{ws} }} }}{{b_{{{\text{rc}}}} }} + 0.407} \right)} \right],$$
(20)

where Q is the normal force; Lc is the contact length between the roller and wavy race; ν1 and ν2 are the Poisson's ratio of the materials of the roller and race, respectively; E1 and E2 are the corresponding elastic modulus; Rr is the radius of the roller; brc is the roller–wavy race contact width, which can be calculated by

$$b_{{{\text{rw}}}} = \sqrt {\frac{{4Q}}{{\uppi L_{{\text{c}}} }}\frac{{R_{{\text{r}}} R_{{\text{w}}} }}{{R_{{\text{r}}} + R_{{\text{w}}} }}\left( {\frac{{1 - \nu _{1}^{2} }}{{E_{1} }} + \frac{{1 - \nu _{2}^{2} }}{{E_{2} }}} \right)} .$$
(21)

The contact stiffness between the roller and wavy race is calculated by

$$K_{{{\text{rw}}}} = \frac{{{\text{d}}Q}}{{{\text{d}}\delta _{{{\text{rw}}}} }}.$$
(22)

Therefore, considering the time-varying displacement and stiffness excitations induced by the race waviness, Eqs. (1) and (2) can be, respectively, developed as

$$\left\{ {\begin{array}{*{20}l} {N_{{{\text{in}}j}} = K_{{{\text{ew}}j}} \left[ {Z_{{{\text{in}}}} \sin \sigma _{j} + X_{{{\text{in}}}} \cos \sigma _{j} - \frac{e}{2} + \varDelta _{j} } \right]_{ + }^{n} } \hfill \\ {N_{{{\text{ou}}j}} = N_{{{\text{in}}j}} + M_{{\text{r}}} \omega _{{{\text{o}}j}}^{{^{2} }} R_{{\text{m}}} } \hfill \\ \end{array} } \right.\;\;\;\;\left( {j = 1,2, \ldots ,N_{{\text{b}}} } \right),$$
(23)
$$K_{{{\text{ew}}j}} = \frac{1}{{\left[ {\left( {1/K_{{{\text{iw}}j}} } \right)^{n} + \left( {1/K_{{{\text{ow}}j}} } \right)^{n} } \right]^{n} }}\;\;\;\;\;\left( {j = 1,2, \ldots ,N_{\text{b} } } \right),$$
(24)

where Kewj is the time-varying equivalent contact stiffness between the inner and outer races via the jth roller; Kiwj and Kowj are the time-varying contact stiffness between the jth roller and wavy inner and outer races, respectively; Δj is the displacement excitations at the angular position of the jth roller, which can be calculated as

$$\varDelta _{j} = \varDelta _{{{\text{iw}}j}} + \varDelta _{{{\text{ow}}j}} \;\;\;\;\left( {j = 1,2, \ldots ,N_{\text{b} } } \right),$$
(25)

where Δiwj and Δowj are the time-varying displacement excitation induced by inner and outer race waviness at the jth roller, respectively.

The detailed power transmission path and mechanical structures of the traction motor and its support bearings are comprehensively considered in this locomotive-track coupled dynamics model. To solve the motion equations of this system with a large degrees of freedom, a hybrid integration method is adopted here. Considering the time-varying excitation and nonlinear factors of the vehicle and rolling bearing subsystems, the fast explicit integration method [33] and the fourth-order Runge–Kutta integration algorithm [34] are used to solve the motion equations of the locomotive-track coupled system and the rolling bearing, respectively. More detailed information on the more complete dynamic model of rolling bearings, dynamic equations, inter-force calculation, and numerical integration algorithm can be referred to our previously published works [21, 23]. The calculation flowchart of the proposed dynamics model is shown in Fig. 5.

Fig. 5
figure 5

Flowchart of the calculation process

Full size image

3 Result analysis and discussions

To analyze the dynamic responses of the traction motor at the bearing position under the effect of the surface waviness and vehicle vibration, an HX locomotive is simulated to run in a straight line. The running speed of the locomotive is approximately 80 km/h. The dynamic parameters of the locomotive-track coupled system, the design parameters of the motor bearings, the tractive characteristics curve, and the measured track irregularities are given in Ref. [23]. In this study, the distributed defect is assumed to individually occur at the inner or outer race of the driving end motor bearing which has 17 rollers. The radii of the roller, inner, and outer races are 9.5, 53.5, and 72.5 mm, respectively. The equivalent length of the roller is 40 mm. The radial clearance is 1 μm. In addition, the corresponding characteristic frequencies of the bearing and the gear mesh frequency are listed in Table 1.

Table 1 Characteristic frequencies of the traction motor
Full size table

The uniform surface waviness directly changes the geometry topography of the race; consequently, the contact stiffness and interactions between rollers and the race are significantly changed. In the rotor–bearing system, the time-varying radial clearance and contact stiffness between the roller and race are considered as the time-varying displacement and contact stiffness excitations induced by the surface waviness of bearing. Under the external (e.g., vehicle vibration and gear mesh) and internal excitations (e.g., dynamic eccentric force, rub-impact force, and so on) during the operation of the locomotive, the traction motor with the faulted motor bearing and its neighboring components in the locomotive subsystem will have more complex fault characteristics. Take the 17th inner/outer race waviness with the amplitude of 4 μm as an example; the geometry topography and the contact stiffness between the roller and race versus angular position of the inner/outer race are shown in Figs. 6 and 7, respectively. In this case, the vertical vibrations of the components of the locomotive (e.g., the car body, bogie frame, motor, and wheelset) in the frequency spectrum under the effect of inner/outer race waviness are shown in Figs. 8 and 9, respectively. It can be seen that the surface waviness of motor bearing can significantly affect the dynamic responses of the bogie and wheelset via the vibration transmission and gear mesh, especially in the longitudinal direction. It should be noted that through the analysis of the amplitudes of frequency-domain signals, the car body and bogie frame are affected less by the race waviness owing to the energy loss during the vibration transmission, while the traction motor and wheelset are sensitive to this kind of fault in the locomotive subsystem. In order to analyze the interactive mechanism between the roller and inner/outer race waviness, the corresponding roller–race contact forces are extracted, which are shown in Figs. 10 and 11, respectively. It can be seen that the rotational frequency of the cage dominates the interaction between the roller and race, while the inner/outer race waviness can excite or intensify the excitation of wave passage frequency (WPF = Nb(fs−fc))/roller pass frequency of outer race (RPFO). Therefore, the WPF, RPFO, and their harmonics can be used as criteria for the inner and outer race wavinesses of the motor bearing, respectively.

Fig. 6
figure 6

Dynamic excitation induced by waviness of inner race: a radius of inner race and b roller–inner race contact stiffness variation versus angular position of the inner race

Full size image
Fig. 7
figure 7

Dynamic excitation induced by waviness of outer race: a radius of outer race, and b roller–outer race contact stiffness variation versus angular position of the outer race

Full size image
Fig. 8
figure 8

Effect of inner race waviness on locomotive subsystem: a car body, b bogie frame, c motor, and d wheelset. WPF = Nb(fs−fc) is the wave passage frequency

Full size image
Fig. 9
figure 9

Effect of outer race waviness on locomotive subsystem: a car body, b bogie frame, c motor, and d wheelset

Full size image
Fig. 10
figure 10

Contact forces between the roller and inner race with waviness: a time history and b frequency spectrum

Full size image
Fig. 11
figure 11

Contact forces between the roller and outer race with waviness: a time history and b frequency spectrum

Full size image

In this section, the vertical and longitudinal vibration accelerations of the traction motor at the fault support bearing position are extracted to better reflect the fault features of the surface waviness; the root-mean-square (RMS) and peak–peak value (PPV) are used to describe the shockwave's energy induced by the race waviness.

3.1 Effect of inner race waviness

For investigating the effect of the inner race waviness, vibration accelerations of the traction motor at fault support bearing position are extracted from the simulations in which the inner race wavenumber varies from 0 to 39 (0, 7, 12, 17, 22, 29, 34, and 39). When Nw = 0, the rolling bearing is healthy. Besides, the maximum amplitude of the waviness is 4 μm. The variation trend curves are shown in Fig. 12. From the statistical indicators (e.g., RMS and PPV), it can be seen that the inner race waviness intensifies the internal interactions between the components of the rolling bearing and induces the abnormal vibration of the traction motor. In addition, if the wavenumber is the number of rollers or an integer multiple thereof, namely, Nw = 17 or 34, there will exist peak values for the statistical indicators versus wavenumbers.

Fig. 12
figure 12

Variations of statistical indicators of vibration accelerations of the motor at fault support bearing position versus the inner race wavenumber: a RMS and b PPV

Full size image

Under the excitations induced by surface waviness with different wavenumbers (e.g., Nw = 12, 17, and 19), the corresponding frequency responses of traction motor at fault support bearing position in the vertical direction are displayed in Fig. 13. It can be seen that the gear mesh is an extremely critical excitation for the rotor–bearing system. By comparison with the results of the healthy traction motor, a variety of fundamental frequencies (e.g., WPF and pNbfc ± qfs (p and q are integers)) and their harmonic components can be captured in the frequency spectrum. However, the eighth to twelfth harmonics of WPF dominate the vibration of the traction motor in the high-frequency region when Nw = 17, while for Nw = 34, the even–order harmonics of WPF, e.g., eighth, tenth, and twelfth, dominate the traction motor vibration in the high-frequency region. A similar phenomenon can be observed in the longitudinal direction. The research results conform to the conclusions in Refs. [7, 12]; however, the side-band frequencies are covered by the environmental vibration and gear mesh.

Fig. 13
figure 13

Vertical vibration accelerations of the motor at fault support bearing position in frequency spectrum: a Nw = 13, b Nw = 17, and c Nw = 34

Full size image

3.2 Effect of outer race waviness

To analyze the effect of outer race waviness on the rotor–bearing system, the vibration accelerations of the traction motor at driving end support bearing are extracted from the simulations with the same dimensions of waviness as in the previous section. The corresponding statistical indicators and frequency responses are displayed in Figs. 14 and 15. As shown in Fig. 14, the intensified vibration will occur, if the outer race waviness is an integer multiple of the number of rollers in the motor bearing. Through analyzing the frequency responses of the traction motor, it can be seen that, in the high-frequency region, the harmonic components of the gear mesh frequency are covered, while the harmonic components of RPFO dominate the high-frequency vibration of the traction motor. When Nw = 34, the effect of the even harmonics of RPFO is more significant. It can be concluded that the high-frequency interactions between rollers and race waviness can alter the dynamic responses of the traction motor significantly, especially when the wavenumber is an integer multiple of the number of rollers.

Fig. 14
figure 14

Variations of statistical indicators of vibration accelerations of the motor at fault support bearing position versus the outer race wavenumber: a RMS and b PPV

Full size image
Fig. 15
figure 15

Vertical vibration accelerations of the motor at fault support bearing position in frequency spectrum: a Nw = 13, b Nw = 17, and c Nw = 34

Full size image

3.3 Effect of amplitude of surface waviness

Considering the machining error of the rolling bearing, the maximum amplitude of race waviness varies from 0 to 16 μm (0, 4, 8, 12, and 16 μm) to investigate the effect of the amplitude of waviness on the dynamic responses of the rotor–bearing system. When Δw = 0 μm, the rolling bearing is healthy. The race wavenumber is assumed as 17. The variation curves of statistical indicators of the vibration accelerations of the traction motor at the fault bearing position with respect to different maximum amplitudes of inner/outer race waviness are shown in Figs. 16 and 17. The trends that the RMS and PPV increase with the maximum amplitude of waviness are obvious owing to the increases in time-varying displacement and contact stiffness excitation between the roller and waviness. Therefore, controlling the amplitude of surface waviness is an effective way to reduce noise and improve the dynamic performance of the traction motor.

Fig. 16
figure 16

Variations of statistical indicators of vibration accelerations of the motor at fault support bearing position versus amplitude of inner race waviness: a RMS and b PPV

Full size image
Fig. 17
figure 17

Variations of statistical indicators of vibration accelerations of the motor at fault support bearing position versus amplitude of outer race waviness: a RMS and b PPV

Full size image

4 Conclusion

In this study, an excitation model coupling the time-varying displacement excitation and the time-varying contact stiffness excitation is adopted to analyze the dynamic responses of the traction motor bearing with a uniform surface waviness during the locomotive operation process. In addition, a locomotive-track spatially coupled dynamics model with detailed traction power transmissions is applied to provide the dynamic loads (e.g., the time-varying gear mesh forces and dynamic suspension forces) for the traction motor system. The results indicate that the surface waviness can intensify the interactions between the roller and the race and further increase the vibrations of the traction motor and its neighbor components of the locomotive. As the wavenumber of inner/outer race waviness changes, the statistical indicators (e.g., RMS and PPV) of vibration accelerations of the traction motor will achieve their peak values when the wavenumber is equal to an integer multiple of the number of rollers. Because the inner/outer race waviness can excite or intensify the excitation of WPF/RPFO, WPF, RPFO, and their harmonics can be the basis of the surface waviness diagnosis for the motor bearing. In addition, the vibration accelerations of the motor and its adjacent components increase with the amplitude of the surface waviness. For reducing the vibration and noise of the traction motor, it is helpful to control the amplitude of the waviness and avoid the wavenumber being an integer multiple of the number of the rollers.