Speed prediction models for car and sports utility vehicle at locations along four-lane median divided horizontal curves

Abstract

Sites with varying geometric features were analyzed to develop the 85th percentile speed prediction models for car and sports utility vehicle (SUV) at 50 m prior to the point of curvature (PC), PC, midpoint of a curve (MC), point of tangent (PT) and 50 m beyond PT on four-lane median divided rural highways. The car and SUV speed data were combined in the analysis as they were found to be normally distributed and not significantly different. Independent parameters representing geometric features and speed at the preceding section were logically selected in stepwise regression analyses to develop the models. Speeds at various locations were found to be dependent on some combinations of curve length, curvature and speed in the immediately preceding section of the highway. Curve length had a significant effect on the speed at locations 50 m prior to PC, PC and MC. The effect of curvature on speed was observed only at MC. The curve geometry did not have a significant effect on speed from PT onwards. The speed at 50 m prior to PC and curvature is the most significant parameter that affects the speed at PC and MC, respectively. Before entering a horizontal curve, drivers possibly perceive the curve based on its length. Longer curve encourages drivers to maintain higher speed in the preceding tangent section. Further, drivers start experiencing the effect of curvature only after entering the curve and adjust speed accordingly. Practitioners can use these findings in designing consistent horizontal curve for vehicle speed harmony.

Introduction

The speed at which vehicles operates in free-flow condition is known as the vehicle operating speed [1]. For a highway segment, it is generally represented by the 85th percentile speed. Researchers had extensively studied the influence of highway geometry on vehicle operating speed and developed operating speed prediction models for different highway segments such as the midpoint of the curve (MC), preceding tangent sections and point of curvature (PC). However, these models vary largely in modeling technique, explanatory variables considered and its coefficients. It might be due to the differences in driver behavior and road geometrics [2]. Hence, no single model is universally acceptable and none of these studies provide an integrated model to predict vehicle speed along a horizontal curve starting from the preceding tangent to the succeeding tangent section.

Most of the available studies on vehicle speed prediction are for two-lane rural highways. The speed characteristics of four-lane divided rural highways are expected to be different from those of two-lane rural highways due to the absence of opposing vehicles, availability of wider pavement, greater opportunity to pass a slow-moving vehicle, etc. In developing countries like India, the two-lane undivided rural highways are generally upgraded to four-lane median divided highways to add capacity. These highways often have at-grade intersections and median openings at certain intervals. The effect of highway geometry on vehicle operating speed in such facilities is not studied extensively. It could be useful in evaluating the geometric features of a horizontal curve section for consistency and safety.

Geometric features of horizontal curves such as inverse of radius (or curvature), curve length and vehicle speed on preceding tangent section influence operating speed at the midpoint of a two-lane rural highway curve [2]. However, speed on the tangent section depends upon preceding and succeeding curve geometry. It was observed that curve radii of 400 m and higher have an insignificant effect and radii above 800 m have no effect on vehicle operating speed [3, 4]. Furthermore, the effect of a horizontal curve on vehicle operating speed is significant in flatter gradient [5]. Horizontal curve radius is the most common independent parameter in the operating speed prediction models at MC [3, 6,7,8]. Other than MC, speed characteristics of vehicles at the beginning and end of a curve have also been studied [6, 9, 10]. Drivers can start decelerating before entering a horizontal curve. Therefore, Poe et al. [11] measured the passenger car speed at a distance of 150 m prior to the PC and 150 m beyond the point of tangent (PT). Similarly, Jacob and Anjaneyulu [3] measured it at a distance of 60 m prior to the PC. However, these studies are for the two-lane rural highways.

Researchers have developed lane-wise operating speed prediction models for the multilane highways [12,13,14]. The mean speed in a lane may depend on the mean speed in the adjacent lane, posted speed limit, access density, land use, presence of a signalized intersection, etc. [13] and the 85th percentile speed on the median width, right shoulder width, presence of access and posted speed limit [14]. However, these studies are based on traffic with stronger lane discipline. Nama et al. [5] extensively studied the speed characteristics of passenger car and heavy commercial vehicle with weak lane discipline but did not provide a speed prediction model. On the other hand, Sil et al. [15] developed the speed prediction model for passenger cars at MC only. Previous studies predominantly used regression analysis for model development [3, 15,16,17,18,19,20]. Such analyses are easy to use and understand and have the ability to incorporate and analyze a large number of variables.

Vehicle speed data collected on Indian highways indicate that speed of trucks is significantly lower than that of passenger cars [5, 19]. Furthermore, passenger cars are frequently found to travel at speed almost equal to, if not higher than, the design speed of the horizontal curves. Trucks, on the other hand, travel at lower than the design speed [5]. All prevalent vehicle types should be considered in speed studies. In India, cars with engine capacity 1.4 L or less and length 4 m or less are predominant. Also, utility vehicles or sports utility vehicles (SUVs) with engine capacity 1.5 L or more, length 4 m or more and ground clearance 170 mm or above are considerable in number.

Vehicle speed prediction models along a horizontal curve starting from the preceding tangent section to succeeding tangent section of four-lane median divided rural highways are not available in the existing literature. Such models can help highway designers to assess geometric features for speed harmony along a horizontal curve. Therefore, the primary objectives of this study are

• analyze the speed characteristics of cars and SUVs along the horizontal curves of four-lane median divided rural highways,

• identify the effect of geometric features on car and SUV driver’s speed choice behavior along the horizontal curves, and

• develop operating speed prediction models applicable at various locations along the horizontal curves.

Site selection and data collection

Though with varied geometric features, the sites selected by researchers met the following properties [2, 9, 16]:

• Sites with physical features or land use that may affect normal driving behavior such as narrow bridges, schools, factories, recreational parks and intersection are avoided.

• Sections with embankment height exceeding 3 m are protected by guardrails.

• Sites with low average annual daily traffic (AADT) are considered to ensure free-flow condition.

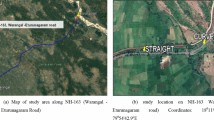
In this study totally eleven sites meeting these properties were selected along National Highway No. 3 between Vadape and Nasik in Maharashtra, India. It is a four-lane median divided rural highway predominantly in rolling terrains. Except for geometric features, these sites are almost identical and meet the IRC:SP:84–2014 [21] design guidelines. The radius of these sites varies from 90 to 430 m and curve length from 100 to 525 m, whereas the superelevation and transition length are 5% and 50 m, respectively. The gradient of two sites meets the limiting gradient of ± 5% and all other meets the ruling gradient of ± 3.3%. These details were obtained from the as-built plan and profile drawings provided by the National Highways Authority of India (NHAI) and Mumbai Nasik Expressway Limited (MNEL). The sites considered have bituminous pavement with standard 3.5 m wide lanes and 1.5 m wide paved shoulder. The typical image of a site is given in Fig. 1.

Fig. 1

Typical study site

The speed data of cars and SUVs were collected at five different locations such as 50 m prior to the point of curvature (PC50), the point of curvature (PC), midpoint of curve (MC), point of tangent (PT) and 50 m beyond the point of tangent (PT50). These locations are illustrated in Fig. 2. The vehicle speed at PC50 signifies the speed in tangent section, at PC the speed while entering a horizontal curve, at MC the speed that driver considers appropriate for a curve, at PT the speed while exiting a horizontal curve and at PT50 the speed that a driver considers appropriate beyond a curve. Video cameras mounted on tripods at a height of 1.8 m and placed on the roadside, outside driver’s cone of vision, were used for data collection. At each location of a site, 15 m wide traps were marked on the pavement. The video data at all five locations of a site were recorded simultaneously during daytime and in fair weather condition for about three hours. All data were obtained in the months of May, June and September 2016.

Fig. 2

Data collection setup

Data extraction and preliminary analysis

The video data collected in the field were played frame by frame to obtain the time taken by each vehicle to traverse the 15 m wide trap. Equation (1) was used to calculate the free-flow speed of cars and SUVs from it. For the free-flow condition, researchers had considered the threshold time headway between 4 and 6 s [22,23,24,25]. In this study, it was considered as 5 s.

$$V = \frac{15 \times 3.6}{{t_{2} - t_{1} }} ,$$

(1)

where V is the vehicle speed in km/h, t₁ is the time in seconds when the front tire of a vehicle touches the first line of the trap, and t₂ is the time in seconds when the front tire of the vehicle touches the second line of the trap.

The descriptive statistics of free-flow speed data are shown in Table 1. It can be observed that the average of mean speed and the 85th percentile speed decreases as a vehicle approaches MC and increases thereafter. On the other hand, except for the mean speed of SUV, the standard deviation increases till PT and decreases thereafter. It implies that the influence of horizontal curves on vehicle speed intensifies near MC and exhibits higher variations due to varying geometric properties of different horizontal curves considered. The car and SUV speed dataset are analyzed for normality using Jarque–Beratest. The obtained p values at 95% confidence interval indicate that the normality of car and SUV speed cannot be rejected.

Table 1 Descriptive statistics of mean and the 85th percentile speed of car and SUV

In Table 1, it can be observed that the descriptive statistics for the mean and the 85th percentile speed of car and SUV at various locations are comparable. Therefore, car and SUV speed data are reviewed for similarity. For this, the mean speed and the 85th percentile speed of cars and SUVs are compared using analysis of variance (ANOVA) and the 85th population quantiles proposed by Hou et al. [26], respectively. The null hypothesis for these two tests is given below:

Null hypothesis for mean speed:

The mean speeds of cars and SUVs at a location are equal

Null hypothesis for the 85th percentile speed:

The 85th percentile speeds of cars and SUVs at a location are equal

The obtained p values for the two hypothese at 95% confidence limit at all locations of all sites are shown in Table 2. These values indicate that the null hypothese for the mean and the 85th percentile speed cannot be rejected. In other words, the mean and the 85th percentile speed of car and SUV are not significantly different. Hence, the speed data of car and SUV are combined and referred as speed data of car in further analysis.

Table 2 The p values for comparing car and SUV speed data

Model development and analysis

Model development

In this study, the speed prediction models for all the five locations (i.e., PC50, PC, MC, PT and PT50) are developed using regression analysis. The field geometric data did not present significant variations in lane width, shoulder width and superelevation. Hence, these parameters are not considered in the model development. The geometric parameters that showed significant variations and, therefore, considered in the model development are horizontal curve radius (R), curvature (1/R), curve length (L_c), deflection angle (Δ), and gradients at PC50 (G_PC50), PC (G_PC), MC (G_MC), PT (G_PT) and PT50 (G_PT50). The 85th percentile speed at the preceding location is also considered in developing the prediction models for PC (V_85PC), MC (V_85MC), PT (V_85PT) and PT50 (V_85PT50). For example, the 85th percentile speed at PC50 is considered in developing the model for PC. The combinations of dependent and independent parameters used in developing the speed prediction models are provided in Table 3. The primary motivations for selecting these combinations are as follows:

Table 3 Combination of dependent and independent parameters

• Vehicle speed at a location depends on highway geometry and roadside environment visible to the driver from the preceding section.

• Vehicle speed at a location also depends on its speed in the preceding section.

• Vehicle speed at PC50 reflects driver’s desired free-flow speed on a tangent and it may be influenced by the curve visible ahead.

• Drivers start paying attention to a horizontal curve from about 50 m prior to the beginning of the curve.

It is clear that R and 1/R are highly correlated. Hence, either R or 1/R should be adopted as the possible explanatory variable in the developed models. As per the fundamental geometric property of a circle, R (or 1/R), L_c and Δ are related. One of these three parameters can be easily obtained from the other two. Hence, any two of them are sufficient in the developed models. The vehicle speeds at various locations are expected to be correlated. Therefore, one vehicle speed parameter (i.e., vehicle speed in the preceding section) should be sufficient as the possible explanatory variable in the developed models. The 85th percentile speed prediction models are developed by stepwise linear regression using the Statistical Package for Social Sciences (SPSS). Out of the eleven, eight sites (about three-fourths) are used for developing the models. The remaining three sites are used for model validation. The obtained models and corresponding adjusted R² values are shown in Eqs. (2–6).

$$V_{{85{\text{PC}}50}} = 83.823 + 0.033L_{\text{c}} ,\;R_{\text{adj}}^{2} = 0.474.$$

(2)

$$V_{{85{\text{PC}}}} = 33.981 + 0.576V_{{85{\text{PC}}50}} + 0.015L_{\text{c}} ,\;R_{\text{adj}}^{2} = 0.949.$$

(3)

$$V_{{85{\text{MC}}}} = 38.735 - \frac{1461.805}{R} + 0.56 V_{{85{\text{PC}}}} + 0.018L_{\text{c}} ,\;R_{\text{adj}}^{2} = 0.986.$$

(4)

$$V_{{85{\text{PT}}}} = 4.440 + 0.949V_{{85{\text{MC}}}} ,\;R_{\text{adj}}^{2} = 0.898.$$

(5)

$$V_{{85{\text{PT}}50}} = 17.189 + 0.830V_{{85{\text{PT}}}} ,\;R_{\text{adj}}^{2} = 0.886.$$

(6)

All explanatory variables in the developed models are significant at 95% confidence level. It can be observed that the explanatory variables affecting the 85th percentile speeds at the five locations vary along the curve. Length of the curve is one of the explanatory variables affecting the 85th percentile speed at PC50, PC and MC, whereas the 85th percentile speed in the preceding section of a highway is one of the explanatory variables for all locations except PC50. The 85th percentile speed at MC is also influenced by 1/R. It can be observed that the adjusted R² value of the model for PC50 is the lowest. This location is part of the tangent section and low adjusted R² for speed prediction models of a tangent section is not very uncommon. For example, the model developed by Fitzpatrick et al. [20] had the adjusted R² value of 0.54. These values improve till MC and start declining thereafter. Additional parameters (not considered in this study) may be needed for better explanation of the 85th percentile speed at PC50, PC, PT and PT50. Speed in the preceding section and posted speed limit are not considered in developing the model for PC50. It may help explain the 85th percentile speed at PC50 better. However, the preceding section speed would make the proposed model field dependent and cannot be used in design and consistency evaluation of highway geometric features.

Sensitivity analysis

The sensitivity of the explanatory variables shown in Eqs. (2–6) is assessed using their standardized ß coefficients. These coefficients are indicated in Table 4. It is observed that between L_c and V_85PC50, the 85th percentile speed model at PC is more sensitive to V_85PC50. Likewise, among L_c, V_85PC and curvature (1/R), the 85th percentile speed model for MC is most sensitive to curvature.

Table 4 The standardized ß coefficient of explanatory variables

Model validation

The obtained models are validated for the three sites not used in the model development. The required parameters and the predicted 85th percentile speeds are presented in Table 5. It can be observed that the maximum error in predicting the 85th percentile speed at PC50, PC, MC, PT and PT50 is 8.1%, 6.0%, 8.2%, 4.9% and 2.3%, respectively. The root mean square error at PC50, PC, MC, PT and PT50 is 5.6%, 4.9%, 4.7%, 4.1% and 1.7%, respectively. It indicates that the developed models are reasonably accurate in predicting the 85th percentile speed of cars and SUVs at various locations along a horizontal curve section.

Table 5 Model validation results

Discussion

The developed speed prediction models indicate that the curve length has a significant effect on the 85th percentile speed of cars and SUVs at locations 50 m prior to PC, PC and MC. At the tangent section prior to a horizontal curve, drivers possibly perceive the horizontal curve based on the curve length. A longer horizontal curve provides a smoother transition from one tangent section to another and encourage drivers to choose higher speed. On the other hand, two tangent sections connected by a shorter curve may appear as a kink to the driver and influence them to choose comparatively lower speed. Till PC, curve length is the only geometric feature that affects car and SUV speed. The effect of curvature (i.e., 1/R) on the 85th percentile speed is observed only at MC. It indicates that drivers experience the effect of curvature only after entering the curve and start adjusting speed accordingly. Highway designers can use these findings in deciding appropriate curve radius and length for consistent geometric design with reasonable speed harmony along a horizontal curve. Further, the developed models can be used in estimating the 85th percentile speed and compare it with the design speed to assess the consistency of a designed highway at various locations along a horizontal curve.

The curve geometry does not significantly affect the 85th percentile speed of car and SUV from PT onwards. However, it depends on the speed at MC and indicates that drivers try to reach their desired speed after slowing down near MC. The developed models do reveal that the 85th percentile speed of car and SUV at a section depends on their 85th percentile speed in the preceding section. It conforms to the result in literature [9]. However, the speed prediction models of passenger cars for the four-lane median divided highways available in literature [12,13,14,15] are applicable only at MC and have not considered the effect of speed in the preceding section. The proposed models can consider the speed in the preceding sections and predict the 85th percentile speed of car and SUV for the four-lane median divided highways at PC, MC, PT and PT50. Possibly, it helps in obtaining a model applicable at MC with higher adjusted R² value compared to some of the similar models available in the literature [12, 15].

Conclusion

The primary aim of this study is to understand the effect of highway geometry on vehicle operating speed of cars and SUVs along the horizontal curves on a four-lane median divided rural highway. The car and SUV speed data are found to be normally distributed and not significantly different. Hence, car and SUV speed data are combined in the analysis. The combined 85th percentile speed of car and SUV at various locations of the study sites is found to be dependent on some combinations of curve length, curvature and speed in the immediately preceding section of highway. However, the gradient does not have a significant effect on the combined 85th percentile speed of car and SUV. Most of the sites considered in this study have a gradient within ± 3.3% and drivers can probably maintain their desired speed at these gradients. The independent variables of the obtained speed prediction models are used to provide indications on driver’s perception about a horizontal curve. Highway designers can use it to design as well as to evaluate highway geometric features.

The minimum time headway considered for free-flow condition might affect the overall outcome. It can be studied separately in future. Further, this study does not consider the lateral position of vehicles in developing the speed prediction models. Researchers had developed lane-based speed prediction models [12,13,14]. Hence, the present study can be extended to incorporate lateral position of vehicles in the speed prediction models. This study, like other previous studies, focused on speed behavior of car and SUV during the daytime. The speed behavior in nighttime could be different. Further, the speed behavior of heavy vehicles is expected to be different from car and SUV. Hence, these are the possible future studies to enhance the present findings.