Abstract
A comfortable environment in railway passenger coaches can be regarded as a resource for social consumption during the transport process. Railway passenger comfort benefits (RPCBs) can be regarded as a special generalized cost. In this paper, we select a series of objective and subjective indexes to formulate a quantitative method of calculating the RPCB with considering ticket fares. This method includes three steps: make the initial data dimensionless, calculate the weight of each index, and finally calculate the RPCBs. The proposed method was validated with the data collected from two types of trains: G13 from Beijing South to Shanghai Hongqiao and T109 from Beijing to Shanghai. Also, questionnaire survey was conducted in both trains. After data processing, the results show that there is a linear relationship between the RPCB and ticket fare with a correlation coefficient of 0.9616.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
With the rapid economic growth and high-speed rail network expanding in China, people are more willing to travel by train, and thus, there is an increasing requirement for passenger comfort of train travel. Railway passenger comfort is determined by a combination of physical and psychological factors. A comfortable environment in railway coaches can be regarded as a resource for social consumption, and railway passenger comfort benefits (RPCBs) can be regarded as a special generalized cost.
From the perspective of passengers, they choose to travel by train because they can take a rest and handle their businesses in a comfortable passenger coach. Moreover, during and after journey, passengers will spend less time to get rid of travel fatigue. This means that providing comfortable transport service is one of the most important measures to attract the passengers. Comfort-related indexes have been applied to evaluate the passenger transport service quality [1,2,3].
In China, Railway Construction Project Economic Evaluation Methods and Parameters (Third Edition, in Chinese) [4] is a guidance to investing projects of new railway lines. It points out that the improvement in passenger comfort benefits is one of the most important evaluation indexes needed to be calculated. But the improvement value is neglected in practice, because the calculation approach is incomplete and the basic data are hard to obtain. Most of the current theoretical researches are devoted to establishing the index system which influences the passenger comfort [5, 6], exploring the comfort range of one exact factor [7], introducing some high technologies and facilities that are helpful to obtain the passenger comfort parameters accurately and easily [8, 9], or studying the relationship between the passenger comfort and transportation management [10]. There are no quantitative calculation approaches to calculate passenger comfort benefits, so it is important to find out a new approach, which can be used both in theoretical research and engineering practice.
In this paper we focus on the quantitative calculation approach and application of RPCBs considering ticket fares. The remainder of this paper is organized as follows: In Sect. 2 we give a brief literature review about passenger comfort. In Sect. 3 we introduce the data that will be used to formulate the quantitative calculation approach. Next in Sect. 4 we give a detailed formulation about the proposed quantitative calculation approach considering passenger ticket fare. Then in Sect. 5, in order to test the performance of the methodology presented in this paper, a numerical experiment is carried out by taking the examples of Beijing-Shanghai ordinary-speed rail line and Beijing-Shanghai high-speed rail line in China. Finally, Sect. 6 presents the major conclusions and an outline of future research.
2 Literature review
2.1 Previous researches on passenger comfort
In 1970s, some researches began to establish the index system that influences the passenger comfort, and tried to obtain the assessment results with questionnaire surveys or other methods. Oborne and Clarke [11] carried out a questionnaire survey from Swansea and discussed how to obtain the quantitative assessment data from the survey effectively. Ref. [12] studied the techniques for the passenger comfort assessment, which included two parts: transportation system aspects, such as riding comfort, local comfort, and organizational comfort, and the behavioral aspects. Moreover, Ref. [13] presented an overview about passenger comfort, the concept of comfort, and its relationship to the passenger’s other travel experiences which were discussed and some factors that influence comfort were introduced, including temperature, ventilation, illumination, photic stimulation, pressure changes on the ear, travel length, and task impairment. Richards et al. [14] thought that an individual’s reaction to a vehicle environment depended on both the physical inputs and the individual characteristics, which means that both objective factors and subjective factors should be considered when evaluating the passenger comfort. Vink et al. [15] used more than 10,000 internet trip reports and 153 passenger interviews to gather opinions about aspects, which need to be improved in order to design a more comfortable aircraft interior. They found clear relationships between comfort and legroom, hygiene, crew attention and seat/personal space, and passenger rate in the newer planes significantly better than those in older ones, indicating that attention to design for comfort was effective, and rude flight attendants and bad hygiene reduced the comfort experience drastically. Nan [5] thought the factors affecting passenger comfort included space per capita, travel time, environment in vehicle, service levels. Passengers with different occupations and travel purposes had different demand in comfort. Wang [6] divided the whole comfort evaluation factors into two parts: objective factors and subjective factors, and a comfort evaluation model based on the mixing parameters of support vector machine was established.
Some other researches focused on exploring the comfort range of factors that influence the passenger comfort, for example, the comfort range of vibration, temperature, noise, air pressure. Refs. [16, 17] studied the relationship between the vibration and passenger comfort; both whole-body vibration in humans and vibration in vehicle were involved. Also, Ciloglu et al. [18] investigated and assessed the whole-body vibration and the dynamic seat comfort of aircraft seats under using average weighted vibration, vibration dose values, and the transmissibility data. Ref. [19] gave a brief review of both field and laboratory studies on human reaction to vibration. The laboratory-based studies were used to predict comfort levels for passenger vehicles. As a result, some suggestions were made for vibration in passenger transport vehicles within acceptable range. Thermal comfort (the temperature factor) in passenger coach has been studied for a long time, in order to define a testing and calculation model for thermal comfort assessment of a bus HVAC design and to compare effects of changing parameters on passenger thermal comfort. Pala and Oz [20] carried out a combined theoretical and experimental work during heating period inside a coach, temperatures, air humidity, and air velocities were measured to investigate effects of fast transient conditions on passengers’ physiology and thermal comfort, and the graphs of passengers thermal sensation and thermal discomfort level were used to evaluate the study. Ref. [21] indicated that solar radiation, poor interior insulation, the non-uniformity of the average radiant temperature affected the thermal comfort in vehicles, and the most popular methods for assessing thermal comfort were reviewed. For a better understanding of thermal comfort in a passenger coach by considering the spectral solar radiation, Moon et al. [22] used commercial software (ANSYS Fluent V. 13.0) to predict thermal and flow fields under the operating conditions of a heating, ventilation, and air-conditioning system. As a result, they found that the estimated temperature near the driver and passengers increased by approximately 1–2 °C when considering the spectral solar radiation. In addition, it was found that the predicted mean vote by considering the spectral radiation was higher than that of the case without considering the spectral radiation. Except for the thermal comfort researches devoted to passenger coaches, and some researchers also tried to explore the thermal comfort in transport terminals. For example, in order to find out the thermal perception, preference, and comfort requirements of passengers and terminal staff in three airport terminals in the UK, researchers [23] monitored the indoor environmental conditions in different terminal areas and conducted questionnaire-guided interviews with 3087 terminal users. They found that the neutral and preferred temperatures for passengers were lower than for employees and considerably lower than the mean indoor temperature, and passengers demonstrated higher tolerance to the thermal conditions and consistently a wider range of comfort temperatures, whereas the limited adaptive capacity for staff allowed for a narrower comfort zone. Furthermore, Ref. [24] indicated that except for temperature, some other climate parameters such as humidity and air movement were also important to passenger thermal comfort. Thus, air temperature had the largest weight for comfort predictions; humidity and air draft also had significant effects and should not be neglected. Noise annoyance is another important factor which influences the passenger’s comfort, Park et al. [25] evaluated the noise annoyance in passenger coaches of high-speed train, and the evaluation was undertaken in different conditions such as the stationary noise, unsteady sudden variation in sound, short-term noise. Ahmadpour et al. [26] analyzed whether the factors underlying the passengers’ experience of comfort differed from those of discomfort. The results showed that there were no significant differences between the comfort and discomfort ratings on the pre-giving factors. Another influencing factor for passenger comfort in passenger coach is air pressure. Schwanitz et al. [7] conducted a questionnaire survey with 262 passengers which revealed that pressure variations are rated less important for riding comfort than climatic and spatial aspects (study 1). Also, a laboratory experiment (study 2) in the pressure chamber at the DLR Institute of Aerospace Medicine with 31 subjects investigated the effects of systematic pressure variations on discomfort, to find out air pressure variations inside trains and reduce pressure comfort for railway passengers, while trains were passing through tunnels. Similar comparative test was conducted again [27], a field study on the high-speed railway track Cologne–Frankfurt/Main as well as a simulation study in their pressure chamber TITAN (DLR Institute of Aerospace Medicine) with 31 subjects to investigate pressure comfort for passengers. They found that beside attributes of instantaneous pressure changes, pressure events of the latter significantly influenced current discomfort. The findings in the two papers may inform design engineers to improve train and tunnel design.
In order to obtain the passenger comfort parameters accurately and easily, some high technology and facilities have also been applied. For example, a triaxial accelerometer [8] was used to measure the acceleration and global positioning system (GPS) was used to obtain position detection. After data collection, they designed an embedded system (hardware, firmware, and software) to assess the dynamic motion factors that affect the comfort in public transportation systems. Lin [9] conducted an experiment using the High-Speed Train Generalized Comfort Research Platform in Southwest Jiaotong University Rail Laboratory. A Delphi–AHP method was used to determine the weight for each factor; then, the experiment was designed to test and verify correctness and feasibility of the passenger comfort evaluation process. Silveira et al. [28] compared two different types of shock absorbers’ behavior, symmetrical (linear) and asymmetrical (nonlinear), which were used on passenger vehicles. The final results showed that the asymmetrical system with nonlinear characteristics tends to have a smoother and more progressive performance, for both vertical and angular movements. A lower level of acceleration is essential for improved ride comfort. The use of asymmetrical systems for vibrations and impact absorption can be a more advantageous choice for passenger vehicles.
Higher passenger comfort has also been considered as a necessary operation factor in traffic and transportation management, because the managers want to provide a better service to attract more passengers. To determine whether bus passenger comfort was influenced by driving style, especially the difference expected to occur after training of drivers in economical (fuel efficient) driving, Af [10] did a field study and found that after training of drivers, passengers experienced more comfortable, which means better driving style is helpful to improve the comfort. To ensure the passenger comfort and the cargo safety, Tezdogan et al. [29] used a sea-keeping analysis approach to calculate the operability index of high-speed passenger ships. The evaluation parameters included: the dynamic responses of the ship to regular waves, wave climate of the sea around the ship’s route, and assigned missions of the vessel. [30] analyzed the influence that perceptions of safety and comfort of service have on the choice of river transport by passengers using hybrid choice models incorporating latent variables. The results indicated that older workers attach less importance to the hull condition and safety; comfort was more valued by young workers and by those users with a higher educational level; the space between seats and developing strategies to improve the behavior of other users significantly increased the perceived comfort of the service provided. Márquez et al. [31] used online survey with 244 respondents to determine which factors contribute to comfort when riding a bicycle and found that comfort is influenced by factors related to bicycle components (specifically the frame, saddle, and handlebar), as well as environmental factors (type or road, weather conditions) and the cyclist (position, adjustments, body parts). Respondents indicated that comfort was a concern when riding a bicycle in most situations and they believed that comfort was compatible with performance.
After summarizing and analyzing the previous researches above, three rules are adopted in this work:
-
(i)
The index system that affects the passenger comfort includes both objective and subjective factors.
-
(ii)
The thresholds for one exact factor that influence the passenger comfort are defined.
-
(iii)
We can use the measurement devices such as vibration sensor, air pressure sensor, thermometer, and automated passenger counting to obtain the data of basic objective parameters of the passenger coaches. Questionnaire survey is a way to obtain the initial data of the subjective indicators.
2.2 Method of calculating the improved railway passenger comfort benefits in China
The calculation approach for the improved railway passenger comfort benefits IRPCBs in the Economic Evaluation Methods and Parameters for Construction Project [4] refers to the whole passenger transport process. It can also be seen as the passenger comfort benefit difference before and after the construction of new railway project. In the approach, both subjective and objective factors are used to calculate it. The objective factors include space per capita, vibration, noise, pressure changes, temperature for a railway passenger coach. Subjective factors are the subjective feelings of people in a railway passenger coach, such as seat comfort degree, interior, information services, food services, and health conditions. The IRPCB \(V_{{\text{IRPCB}}}\) is defined as
where P ij is the set of origin and destination OD(i, j), which is related to the new railway project; m is the passenger coach types; Q dij,m is the number of transfer passengers in different transport modes and for different transport routes in one transport mode as well; P 0 m is the set of passenger transport routes without newly built projects; P 1 m is the set of passenger transport routes with new projects; l is a generalized line for path P 0 m or path P 1 m , which represents both one actual line and one connecting line between the starting point and arrival point; Tij,m,l represents the time on the l between any OD(i, j); SPij,m,l is the space per capita on the l between any OD(i, j); ϑij,m,l represents the additional generalized cost per hour of the other related influential factors except space per capita on the l between any OD(i, j), which is generally ignored in practice; E and β are the factors need to be demarcated during the calculation process. After analyzing this formula, we can find the following disadvantages:
-
(i)
Except for space per capita, other objective factors are not considered, which means that it is not a precise formula.
-
(ii)
Usually, it is hard to be applied in practice because the indexes such as ϑij,m,l, E, and β are difficult to obtain.
3 Index adoption and initial data measurement
According to the actual practice and theoretical researches, both objective indicators and subjective indicators have crucial impacts on RPCBs. Objective indicators belong to physical factors during the whole transport process, for example, area per capita in passenger coach, vibration, noise, pressure changes, temperature. Subjective indicators are related to the passengers’ subjective feelings, such as seat comfort, interior decoration of the passenger coach, information services, catering services.
3.1 Objective indicators
We obtained the data of objective indicators by measurement devices, such as the vibration sensor, air pressure sensor, temperature sensor, noise tester, tape measure, automated passenger counting, and passenger coach design drawings. The following six indicators were measured.
-
(1)
Area per capita in passenger coach
Area per capita in passenger coach is a factor that directly affects passenger travel comfort during the rail transport process, and a large area per capita for passenger means high passenger travel comfort. The specific standards are clearly defined in the design specifications for each kind of transport mode. For example, according to the statistical data, the area per capita is 0.57 m2 when the seat utilization rate is 100% in China [5, 6]. In addition, the area per capita in railway passenger coach in other countries is listed in Table 1.
The data of area per capita in passenger coach x 1 m were obtained by the combination of tape measurement, automated passenger counting, and passenger coach design drawings, for the different types of railway coaches.
-
(2)
Vibration
Vibration exists in each transport mode. It is also a major factor affecting passenger comfort. Vibration is generally divided into lateral and vertical vibrations. Humans are more sensitive to lateral vibration. In this paper, we let the ratio of lateral vibration be 0.7 and ratio of vertical vibration be 0.3 [6, 18]. The vibration is used to formulate the operation stability x 2 m .
where A h i and A c i in \({{\text{m}} \mathord{\left/ {\vphantom {{\text{m}} {{\text{s}}^{2} }}} \right. \kern-0pt} {{\text{s}}^{2} }}\) are the lateral vibration acceleration and vertical vibration acceleration; f h i and f c i in \(\text{Hz}\) represent the lateral vibration frequency and vertical vibration frequency; F(f h i ) and F(f c i ) are the vibration frequency correction terms, listed in Table 2.
We used the vibration sensors to obtain the vibration acceleration and frequency in the passenger coach. The vibration sensors recorded the data during the whole testing process, and the averaged values of vibration acceleration and frequency are applied in calculation.
-
(3)
Pressure changes
The air pressure in the railway passenger coach will change during the train operation, and intense pressure fluctuations can cause passenger discomfort and even damage to the body, such as ruptured eardrum. In this paper, the rate of air pressure change is introduced [5, 6]:
where x 3 m in \({{\text{Pa}} \mathord{\left/ {\vphantom {{\text{Pa}} \text{s}}} \right. \kern-0pt} \text{s}}\) is the air pressure change rate and Δp in \({{\text{Pa}} \mathord{\left/ {\vphantom {{\text{Pa}} \text{s}}} \right. \kern-0pt} \text{s}}\) the maximum pressure change. Also, T in °C is the temperature in the railway coach, V is the passenger coach volume in m3, and R is Molar gas constant. Table 3 shows the design values of the maximum pressure change and maximum pressure change rate in some countries.
Pressure and temperature were measured by pressure sensors and temperature sensors. The passenger coach volume was obtained according to coach design drawings.
-
(4)
Noise
High speed usually causes more noise in the passenger coach. Noise pollution has potentially adverse impact on passengers’ health, such as hearing impairment, headache, and neurasthenia. During the train operation process, noise and speed have a linear relationship, i.e., when the speed increases 10 km/h, noise level will increase 1–2 dB, correspondingly. Each kind of transport mode has its own maximum noise level limitation. As for the train operation, if the train speed is 80 km/h, the noise level in the passenger coach should be limited at 68 dB. International Union of Railways (UIC) requires the noise in passenger train should not exceed 65 dB [5, 6]. Also, the average operation speed of TGV-A in France is over 300 km/h, but the noise in passenger coach is 66 dB. We used the noise testers to obtain the actual noise level in the railway passenger coaches.
-
(5)
Temperature
In recent years, passenger coaches are generally equipped with air-conditioning systems. According to passengers’ feedback, there is a great temperature difference between the passenger coach and external environment. Poor air-conditioning and ventilation are source of passenger discomfort, for example, dizziness, sneezing, fatigue, memory loss, muscle and joint pain. IS07730 temperature setting standard is widely used in European countries, which requires the temperature range of human thermal comfort to be 21–24 °C. Also, the standard ASHRAE55-92 used in the USA insists the range of thermal comfort temperature to be 20–23.6 °C. Furthermore, the predetermined temperature boundaries of human skin feeling for hot and cold condition are 20–25 °C. The comfort temperature range is 17–28 °C in China [5–6, 9]. We used the temperature testers to obtain the average temperature in the passenger coaches, and the test data were used to calculate the air pressure change rate.
-
(6)
Passenger travel time
Ergonomics research [6, 9] shows that if the travel time exceeds 6 h, the passengers will feel uncomfortable. Sometimes, the train may be delayed, which can also cause the discomfort of passengers. We obtained the travel time according to the 12,306 Railway Passenger Service Center.
3.2 Subjective indicators
There are five kinds of subjective indicators of interest: health conditions, interior decoration of passenger coaches, information services, seat comfort, and catering services. The five main indicators include 16 subindexes u j , j = 1, 2, …, 16 as shown in Table 4.
We collected the initial passenger evaluation data by conducting questionnaire survey in the passenger coaches. There are m kinds of ticket fare, so the comprehensive subjective indicator data x 7 m can be formulated as follows:
where α j m is the weight for each subindex, for the m kinds of ticket fare; N m is the number of passengers surveyed, and h m,j i is the score of each surveyed passenger toward each subindex, the range of h m,j i being 0–100; if 0 ≤ h m,j i < 60, it means that the surveyed passenger regards this item as an uncomfortable source; if 60 ≤ h m,j i ≤ 100, this item is seen as a comfortable source. We let the average surveyed data \(\bar{h}_{m}^{j}\), \(\bar{h}_{m}^{j} = {{\sum\nolimits_{i = 1}^{{N_{m} }} {h_{i}^{m,j} } } \mathord{\left/ {\vphantom {{\sum\nolimits_{i = 1}^{{N_{m} }} {h_{i}^{m,j} } } {N_{m} }}} \right. \kern-0pt} {N_{m} }}\). Furthermore, if 0 ≤ x 7 m < 60, the comprehensive subjective index is regarded as an uncomfortable factor; if 60 ≤ x 7 m ≤ 100, it is a comfortable factor for passengers.
The weighting coefficient α j m can be obtained using the analytic hierarchy process (AHP) [32]. Here, we used the two-phase AHP to construct the judgment matrix that can meet the consistency requirement [33] and [34]. The procedure is presented as follows:
-
(i)
Constructing the subindex judgment scaling matrix
In the first phase, after the pairwise comparison of all subindexes through a three-scale method (with values of 0, 1, and 2), we built a comparison matrix to calculate the ranking index of the subindexes. In this section, we use i, j to represent the subindexes. H = (hi,j) = {0, 1, 2}is the judgment scale set, in which hi,j = 0 means that subindex i is less important than subindex j; hi,j = 1 means that subindex i is as important as subindex j; and hi,j = 2 means that subindex i is more important than subindex j.
-
(ii)
Constructing the subindex judgment matrix
In the second phase, we constructed the judgment matrix using the range method. If a ij is the ratio of the importance of subindex i to the importance of subindex j, then 1/a ij is the ratio of the importance of j to that of i. According to the range method:
where \(\varvec{A} = \left( {a_{ij} } \right)\) constitutes the consistency judgment matrix; a b is the given relative importance of the pair of range elements, based on a certain standard, and always generally assigned a constant value of a b = 9 [35]. \(b_{i} = \sum\nolimits_{j = 1}^{16} {a_{ij} } ,B = \hbox{max} \left( {b_{i} } \right) - \hbox{min} \left( {b_{i} } \right)\). The weighting coefficient α jk,m can be obtained by
Finally, we conducted a consistency test for the obtained weights. The final results about the 16 subindex weight ϖ n m are presented in Table 7.
4 RPCB calculation approach
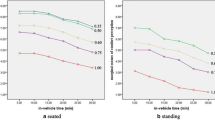
The field research on travelers in Shanghai [36] showed that under the same traveling time conditions, more than 86% of passengers were willing to pay more for a more comfortable traveling environment. The RPCB is regarded as an objective factor when passengers are choosing their travel mode. Shi et al. [37] thought that there is a directly proportional relationship between passenger comfort and travel expenses, but with the increase in travel time and travel costs, the RPCB growth rate is reducing. According to the pricing strategy of passenger tickets in China, in general, longer distance means higher ticket cost, but less unit ticket price. Figure 1 shows the relationship between travel time and passenger ticket cost (a), and the relationship among the travel time, passenger ticket cost, and RPCB (b).
Property
The RPCB is related to both travel time and passenger ticket cost; we can use the following composite function to formulate the RPCB:
Proof
Figure 1a shows that, in general, longer travel distance means more travel time, so we use time to replace distance; if t3 − t2 = t2 − t1, then c3 − c2 < c2 − c1; we can use the following function to formulate the relationship between the travel time and passenger ticket cost:
Figure 1b shows that, for the exact travel time t2, if ticket price c3 > c1, then F(c3, t2) > F(c1, t2). If t3 − t2 = t2 − t1, then we can obtain c3 − c2 < c4 − c3; we can use the following function to describe the relationship between the RPCB, travel time, and passenger ticket cost:
Remark
When we combine t = f(c) and F(c, t), we can use the composite function [23] mentioned above to describe the relationship between the RPCB and the passenger transport ticket fare.
Passenger ticket cost and comfort degree vary with the types of seats. For example, there are three types of tickets in China’s high-speed trains: first-class seat, business-class seat, and ordinary-class seat. The RPCB loss due to train delay is varied for the passengers in different seats, because the first-class seat passengers spend more money to buy the tickets, expecting better service and higher RPCB. The passenger comfort benefit is increased or reduced by the ticket fares.
We collected the information of the passenger ticket prices from the Railway Customer Service Center of China (RCSCC). The passengers have m types of ticket fares, such as 1748 CNY (for a business-class seat), 933 CNY (for a first-class seat), and 553 CNY (for a second-class seat) in one high-speed train from Beijing South to Shanghai Hongqiao. Though the ticket price is different, the passengers on one train have to experience the same vibration, pressure change, temperature, and operation time. The area per capita in passenger coach, however, is quite different, because different types of seat correspond to different train facilities and equipment setting and service.
In order to achieve the non-dimensionalization of initial data, we divide all the objective and subjective indexes into three categories: (1) area per capita in passenger coach, (2) vibration, noise, pressure changes, temperature, and operation time, and (3) subjective indexes. For the m types of seats, the quantitative calculation process of the RPCB is organized as three steps.
Step 1 Non-dimensionalization of initial data
There are seven kinds of obtained initial data x n m , n = 1, 2, …, 7, which need to be non-dimensionalized.
-
(i)
Area per capita in passenger coach
where x 1 m represents the initial area per capita in passenger coach. If X 1 m > 0, it is a comfort factor for passengers; otherwise, it is not helpful to improve the final RPCB. We let the comfort threshold about area per capita in passenger coach x 1 m ≥ 0.57.
-
(ii)
Vibration, noise, pressure changes, temperature, and operation time
where \(\left[ {\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{x}_{m}^{n} ,\bar{x}_{m}^{n} } \right],\forall m,\forall n = 2,3, \ldots ,6\) shows the comfort range for each index. Also, it is helpful to increase the RPCB if X n m > 0; otherwise, it will decrease the final RPCB. In this paper, let the comfortable range of railway vibration 0 ≤ x 2 m ≤ 7, which means if x 2 m > 7, the vibration will become an intolerable factor for passengers in the railway coach. The comfortable range about air pressure change is 0 ≤ x 3 m ≤ 200 \({{\text{Pa}} \mathord{\left/ {\vphantom {{\text{Pa}} \text{s}}} \right. \kern-0pt} \text{s}}\). Also we set that the comfortable range of the noise is 0 ≤ x 4 m ≤ 65 dB, the comfortable temperature range in passenger coach is 17 ≤ x 5 m ≤ 28 °C, and the comfortable railway travel time range is 0 < x 6 m ≤ 6 h.
-
(iii)
Subjective index
The final data of the subjective index will increase the RPCB if 60 < x 7 m ≤ 100; otherwise, it will decrease the RPCB if 0 ≤ x 7 m ≤ 60.
Step 2 Calculate the weight of each index
The two-phase AHP will be used to obtain the weight ϖ n m of each index n. The final results about the seven index weights are presented in Table 7.
Step 3 Calculate RPCB
We use the product of the passenger ticket price P m (CNY) and comprehensive evaluation coefficient η m to represent the passenger comfort benefit value, which is just for an unit calculation result.
5 Numerical experiment and results discussion
5.1 Initial data
Over the past twelve years, China built a lot of railway lines to meet the huge and growing passenger transportation demand. This has resulted in the largest ordinary-speed railway (OSR) network and high-speed railway (HSR) network in the world, with total lines in operation nearly 120,000 km by the end of 2015. In addition to this, continuous high investments have prompted the expanding of China railway network. Thus, the evaluation of passenger comfort benefit for these new railway projects becomes important. The basic operation information of the two trains of G13 and T109 (G13 is a high-speed train, and T109 is a ordinary train) is collected from the China Railway Passenger Service Network (www.12306.com) to test the proposed RPCB calculation method, including train operation time, seat types, and ticket prices. Detailed information is shown in Table 5.
There are four kinds of blocks in G13, including business-class seat (BS), principal seat (PS), first-class seat (FCS), and second-class seat (SCS), and four kinds of blocks in T109, including luxury soft sleeper (LSS), soft sleeper (SS), hard sleeper (HS), and ordinary seat (OS). The test period is the train operation time, 4.92 h for G13 and 15.2 h for T109, respectively. We arranged eight persons for the G13 group and eight persons for T109 group. For the eight persons in each group, four of them used devices to collect the basic operation data. Each of them has a vibration sensor, an air pressure sensor, a temperature sensor, a noise tester, a tape measure, an automated passenger counting. The data of these objective indexes are presented in Table 6. Other four persons conducted the questionnaire survey. According to the number of passengers paying for different seats, different numbers of questionnaires were delivered: 50 in BS, 100 in PS, 100 in FCS, and 200 in SCS, and 50 in LSS, 100 in SS, 200 in HS, and 300 in OS. Finally, we obtained 423 valid questionnaires for G13 and 605 valid questionnaires for T109. Due to space limitations, we only present the final data in Table 6, not including the initial survey data. Only passengers traveling from Beijing to Shanghai were chosen as respondents. As a result, for each kind of seat, we only present the average values \(\bar{h}_{m}^{j}\) in Table 7. The first row shows the average surveyed data \(\bar{h}_{m}^{j}\) and its corresponding weight α j m about the 16 subindexes.
5.2 Calculation results and discussion
According to the proposed RPCB calculation processes, we obtain the following calculation results, shown in Table 8.
The business-class seat in G13 provides the most comfortable traveling condition, but has the most expensive fare. The RPCB for ordinary-speed train seats is lower than that for high-speed railway train generally. The RPCB of LSS is higher than RPCB of SCS and FCS, because the services of luxury soft sleeper (LSS) in T109 are better than of SCS and FCS, passengers have a relatively independent personal space than the other seats, and they have less disturbing factors during the travel, so the they will spend less time to get rid of travel fatigue. The negative values for both hard sleeper and ordinary seat mean that there is no comfort for passengers, and passengers will need more time to recover from tiredness. Furthermore, the high-speed railway has an advantage in time-saving. Figure 2a shows the comparison of the RPCB and passenger ticket fare between the high-speed train and ordinary-speed train; Fig. 2b shows the linear relationship between the RPCB and ticket fare with correlation coefficient R2 = 0.9616, which can be formulated as
where c is the ticket fare.
6 Conclusion and further works
By considering the passenger ticket fare, a quantitative calculation approach for railway passenger travel comfort benefit was formulated. After choosing the objective and subjective indexes, we used measurement devices to collect the data of the objective indexes from two types of railway trains, a high-speed train of G13 from Beijing South to Shanghai Hongqiao and an ordinary-speed train of T109 from Beijing to Shanghai. Also questionnaires were delivered to obtain the initial data of subjective indexes. Then, we processed the initial data with three steps and analyzed the obtained results, finding a linear relationship between the RPCB and ticket fare. The presented RPCB calculation process can be used to calculate the economical benefit of scale by multiplying the total number of passengers. Furthermore, the passenger comfort benefit calculation process is suitable for other kinds of transport modes, but the indexes may be different, so exploring other application of the calculation process will be meaningful and necessary for the future works.
References
Eboli L, Mazzulla G (2011) A methodology for evaluating transit service quality based on subjective and objective measures from the passenger’s point of view. Transp Policy 18(1):172–181
Shen W, Xiao W, Wang X (2016) Passenger satisfaction evaluation model for urban rail transit: a structural equation modeling based on partial least squares. Transp Policy 46:20–31
Zhang K, Zhou K, Zhang F, Zhang K, Zhou K, Zhang F (2014) Evaluating bus transit performance of Chinese cities: developing an overall bus comfort model. Transp Res A 69(69):105–112
Ministry of Housing and Urban-Rural Development of the People’s Republic of China, National Development and Reform Commission of People’s Republic of China, Ministry of Railways of People’s Republic of China (2012) Railway construction project economic evaluation methods and parameters. Beijing. China Planning Press. (in Chinese)
Nan J (2005) Study on comfort demand of passenger travel. Rail Transp Econ 27(6):79–81
Wang G (2013) The data-based appraisal method of riding environmental comfort. Beijing Jiaotong University Master Dissertation
Schwanitz S, Wittkowski M, Rolny V, Samel C, Basner M (2013) Continuous assessments of pressure comfort on a train—a field-laboratory comparison. Appl Ergon 44(1):11–17
Castellanos JC, Fruett F (2014) Embedded system to evaluate the passenger comfort in public transportation based on dynamical vehicle behavior with user’s feedback. Measurement 47:442–451
Lin S (2014) Research of evaluation method and model design on synthesis comfort of high-speed train. Southwest Jiaotong University Master Dissertation
Af Wåhlberg AE (2006) Short-term effects of training in economical driving: passenger comfort and driver acceleration behavior. Int J Ind Ergon 36(2):151–163
Oborne DJ, Clarke MJ (1975) Questionnaire surveys of passenger comfort. Appl Ergon 6(2):97–103
Oborne DJ (1978) Techniques available for the assessment of passenger comfort. Appl Ergon 9(1):45–49
Oborne DJ (1978) Passenger comfort—an overview. Appl Ergon 9(3):131–136
Richards LG, Jacobson ID, Kuhlthau AR (1978) What the passenger contributes to passenger comfort. Appl Ergon 9(3):137–142
Vink P, Bazley C, Kamp I, Blok M (2012) Possibilities to improve the aircraft interior comfort experience. Appl Ergon 43(2):354–359
Oborne DJ (1976) A critical assessment of studies relating whole-body vibration to passenger comfort. Ergonomics 19(6):751–774
Oborne DJ (1977) Vibration and passenger comfort. Appl Ergon 8(2):97–101
Ciloglu H, Alziadeh M, Mohany A, Kishawy H (2015) Assessment of the whole body vibration exposure and the dynamic seat comfort in passenger aircraft. Int J Ind Ergon 45(7):116–123
Oborne DJ (1978) Vibration and passenger comfort: can data from subjects be used to predict passenger comfort? Appl Ergon 9(3):155–161
Pala U, Oz HR (2015) An investigation of thermal comfort inside a bus during heating period within a climatic chamber. Appl Ergon 48:164–176
Damian RM, Danca P, Vartires A, Dogeanu A (2016) An overview of current methods for thermal comfort assessment in vehicle cabin. Energy Procedia 85:162–169
Moon JH, Lee JW, Jeong CH, Lee SH (2016) Thermal comfort analysis in a passenger coach considering the solar radiation effect. Int J Ther Sci 107:77–88
Kotopouleas A, Nikolopoulou M (2016) Thermal comfort conditions in airport terminals: indoor or transition spaces? Build Environ 99:184–199
Maier J, Marggraf-Micheel C (2015) Weighting of climate parameters for the prediction of thermal comfort in an aircraft passenger cabin. Build Environ 84:214–220
Park B, Jeon JY, Choi S, Park J (2015) Short-term noise annoyance assessment in passenger coachs of high-speed trains under sudden variation. Appl Acoust 97:46–53
Ahmadpour N, Robert JM, Lindgaard G (2016) Aircraft passenger comfort experience: underlying factors and differentiation from discomfort. Appl Ergon 52:301–308
Schwanitz S, Wittkowski M, Rolny V, Basner M (2013) Pressure variations on a train-where is the threshold to railway passenger discomfort? Appl Ergon 44(2):200–209
Silveira M, Pontes BR, Balthazar JM (2014) Use of nonlinear asymmetrical shock absorber to improve comfort on passenger vehicles. J Sound Vib 333(7):2114–2129
Tezdogan T, Incecik A, Turan O (2014) Operability assessment of high speed passenger ships based on human comfort criteria. Ocean Eng 89:32–52
Márquez L, Cantillo V, Arellana J (2014) How are comfort and safety perceived by inland waterway transport passengers? Transp Policy 36:46–52
Ayachi FS, Dorey J, Guastavino C (2015) Identifying factors of bicycle comfort: an online survey with enthusiast cyclists. Appl Ergon 46(A):124–136
Saaty TL (1990) Decision making for leaders: the analytical hierarchy process for decisions in a complex world. RWS Publishing, Pittsburgh
Zhu Y, Men ZY, Kan SY (1999) Using AHP to calculate the weights. J Beijing Jiaotong Univ 23:119–122
Vaidya OS, Kumar S (2006) Analytic hierarchy process: an overview of applications. Eur J Oper Res 169(1):1–29
Liu Z, Jiang C, Wang J, Yu H (2015) The node importance in actual complex networks based on a multi-attribute ranking method. Knowl-Based Syst 84:56–66
Yuan J, Ye L (2007) Affect analysis between transit service levels and bus fare adjustment. Price Theory Pract 5:45–46
Shi F, Deng L, Huo L (2007) Boarding choice behavior and its utility of railway passengers. China Railw Sci 28(6):117–121
Acknowledgements
This research was jointly supported by the Traffic and Transportation Engineering Experiment and Comprehensive Innovation Center, School of Transportation and Logistics, Southwest Jiaotong University, Chengdu Sichuan, and subsidized by National Natural Science Foundation of China (71173177), China State Railway Administration of Science and Technology Legal Division (KF2013-020), and 2015 Graduate Innovative Experimental and Practice Program (YC201507103), Southwest Jiaotong University. Also the authors would like to thank the anonymous referees for their valuable comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Huang, W., Shuai, B. A methodology for calculating the passenger comfort benefits of railway travel. J. Mod. Transport. 26, 107–118 (2018). https://doi.org/10.1007/s40534-018-0157-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40534-018-0157-y