Abstract
It has been reported in the past literature that total traffic volume and passenger car volume are affected by snowfall and cold temperature, but trucks are not significantly affected. This paper aims to confirm that the distribution of truck types is not affected by winter weather conditions through combined statistical analysis in the framework of microscopic and macroscopic impact analysis. A micro-level analysis was conducted to investigate the effect of snowfall and temperature on changes in truck type distribution. A macro-level analysis was also conducted to investigate the effect of the months (or seasons) on changes in truck type distribution. Truck traffic data were collected for 5 years at the weigh-in-motion site in Highway 2A, which is used for regional commuters near the City of Leduc, Alberta, Canada. The trucks were subdivided into straight unit truck, single trailer and multi trailer unit and then analyzed by applying a nonparametric Chi-squared test combined with the binomial probability test. As a result of the nonparametric test, the truck type distribution was stable irrespective of the severity of winter weather conditions, which are microscopic factors such as snowfall and temperature, and was not influenced by changes in months and seasons, which are macroscopic factors.
Similar content being viewed by others
Explore related subjects
Find the latest articles, discoveries, and news in related topics.Avoid common mistakes on your manuscript.
1 Introduction
Winter weather conditions affect transportation systems in many ways, such as major interruptions in traffic flow, evacuation from transportation systems, and serious impacts on mobility and safety of transportation system users [1]. The study of the effects of inclement weather on overall traffic volumes has been a common theme for many years in the literature. Datla and Sharma [2] closely examined the impact of winter weather conditions such as cold temperature and snowfall on highway total traffic volume. The study concluded that winter weather conditions cause a variety of variations in total traffic volume and that the magnitude of the variations depends on the time of day, day of week and spatial location of the highway, type of the highway and severity of the weather. However, research published in the literature and other similar studies have been based solely on total traffic data collected by permanent traffic counters (PTCs) without considering passenger cars and trucks separately. Truck traffic data are considered key input for many types of transportation analyses, such as the structural design of pavements, geometric design, highway life cycle analysis and prioritization of highway construction projects. The increasing use of truck data is strongly supported by a rapid and widespread introduction of vehicle classification technologies [3]. However, in spite of its importance in applications, only limited amount of vehicle classification data have been collected by highway agencies, and thus, not much of analytical work has been conducted in the past. Consequently, many characteristics of truck traffic patterns have not been well analyzed and learned by highway agencies in almost all aspects of transportation planning and engineering [4]. In a recent study, Roh et al. [5] conducted dummy variable regression modeling using vehicle classification data collected from WIM system. As a result, it is identified that total traffic volume and passenger cars are affected by snowfall and cold temperatures, but trucks are not affected by snowfall up to 16 cm and cold temperatures below − 30 °C.
This paper is pursued to deepen the understanding of the unique characteristic of trucks in the mixed traffic stream and hence to confirm the conclusions of Roh et al.’s [5] study on trucks. To pursue this, two analyses scaled by micro- and macro-level were conducted to analyze the impact of weather conditions on truck type distribution. As an analysis in macroscopic level, the variations of truck type distribution for two temporal groups were statistically tested: (1) month-to-month variations and (2) season-to-season variations in which the months of November to March representing severe winter conditions are grouped into winter and the remaining months are grouped into non-winter. As an analysis in microscopic level, the variations of truck type distribution for two weather factors were also tested solely for winter season from November to March: (1) snowfalls, which were categorized into three categories according to the amount of snow on the ground, and (2) temperatures, which were categorized into seven cold categories with an equal interval in 5 °C.
To conduct the test, the truck data were in this study subdivided into subgroups such as straight truck, single trailer, and multi trailer unit. The truck data were collected from WIM system for 5 years from 2005 to 2009 at a highway site located on Highway 2A south of the City of Leduc in Alberta, Canada. It should be noted that the portion of truck is 8% in mixed traffic volumes in the study site. Liu [6] investigated the effect of holidays on volume changes using permanent traffic counters (PTCs) data collected over a 10-year period on the Canadian Alberta highway network. He compared the traffic pattern of typical days and the traffic patterns of holidays with the help of the Chi-squared test combined with the binomial test and verified the statistical significance of the occurrence of traffic peak during the holidays. Based on the literature, to reach a comprehensive statistical conclusion on whether truck type distribution is affected by two temporal groups and two weather factors, a Chi-squared test combined with a binomial test designed in this study as statistical validation procedure was applied.
2 Literature review
Many studies in the literature reported quantitative analysis on the association of traffic volumes with weather factors by measuring the magnitude of reductions in traffic volumes due to different weather conditions. Datla and Sharma [2] studied thoroughly the impact of cold and snow on daily and hourly traffic volumes on Alberta provincial highway network in Canada. Hanbali and Kuemmel [7] studied traffic volume reductions due to snow storms on rural highways in the USA. Hassan and Barker [8] studied the association of traffic variations with meteorological parameters such as minimum and maximum temperatures, precipitation of snow and rain, amount of snow on ground surface and hours of sunshine for the region of Lothian, Scotland. Knapp and Smithson [9] analyzed average traffic reductions on interstate highways in Iowa State during winter storms. Keay and Simmonds [10] reported the association of rainfall and other weather factors with traffic volume on urban arterials in Melbourne, Australia. A chain reaction mechanism is suggested by Colyar et al. [11] to explain the impact of weather events on the traffic operation. It is also indicated by the some studies [12, 13] that a reduction in traffic during adverse weather conditions are mainly resulted from the trip adjustments such as leaving for work early, and an avoidance of unnecessary and discretionary trips. Maze et al. [14] reported a strong correlation between the percentage reduction in traffic volume and wind speed and visibility during snowy days on Inter-state Highway 35 in northern rural Iowa, USA. Changnon [15] studied the impact of variations in summer precipitation patterns on travel patterns in Chicago area. It should be noted that none of the previous studies have adopted the novel combined statistical methodology to conduct an investigation on the impact of micro- and macro-level weather changes on the truck type distribution.
3 Study data
Alberta Transportation (AT) manages and rehabilitates the Alberta highway network in Canada and archives traffic flow data collected in real time using the WIM system. The six WIM sites in the Alberta highway network were established in 2004 and have constantly been collecting data on vehicle configuration information such as axle number and spacing, including traffic characteristics such as speed and weight. These data have been used as data input for programs such as Alberta’s Strategic Highway Research Program (ASHRP) and Long-Term Pavement Performance (LTPP) [16].
The study was conducted as a case study using data collected over 5 years from 2004 to 2009 at a single WIM site south of Highway 2A near the City of Leduc, Alberta, Canada. Functionally, the highway serves for both local and regional commuter traffics with approximately 7,000 average annual daily traffic (AADT). The portion of truck traffic is about 8% of the total traffic. The weather data for the study are obtained from Environment Canada’s Climate Database [17]. Environment Canada manages nearly 8,000 weather stations across the country to collect climatologically data. Each of these weather stations provides detailed weather parameters such as maximum, minimum and mean temperature (measured in °C, centigrade), total rain (millimeters), total snow (centimeters), total precipitation (millimeters) and the amount of snow on ground (centimeters) on a daily basis.
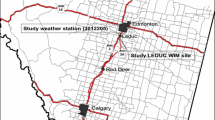
Defining the distance from the weather station to WIM site, in which the meteorological conditions could be assumed homogeneous, is an important task to reliably predict changes in traffic volume due to weather conditions. A literature review has been conducted on reasonable ways to specify the distance from the WIM to the surrounding weather stations in which homogeneous climatic conditions are ensured. To complete this, a thematic base map displaying all weather stations across province including the study WIM site was developed by applications of Geographical Information Systems (GIS). According to the research conducted by Datla and Sharma [2], the climatic condition within the radius of 16–25 km from the traffic counting facilities can be considered homogeneous. Based on the results of the study, weather stations within that distance range were identified on the map using a proximity analysis provided by ArcGIS 10 [18]. The weather station apart by a distance of 13 km from the WIM site was selected as appropriate candidate. It is labeled as 3012205 hereafter and has perfect weather data without any missing portions.
4 Methodology
Another important thing to keep in mind is to select a reliable classification algorithm to ensure high accuracy of the vehicle classification results and to obtain enough truck traffic samples to be used for statistical analysis. After a comprehensive literature review of vehicle classification techniques and their applications, Federal Highway Administration’s (FHWA) scheme F was applied to raw WIM data as the first phase of classification. During the first round of classification, the FHWA scheme F developed by Maine Department of Transportation [19] was found to be easily applicable in practices. In contrast to ease of use in practice, the ambiguity of axle spacing, which is an indicator used to classify vehicles into bins prepared for each vehicle type, has been pointed out as a weakness for this method [20]. In order to overcome the weakness of FHWA scheme F, the second classification procedure, which is based on the concept of Probabilistic Neural Network (PNN) algorithm, is applied to vehicular records not classified in the first phase classification. The detailed description of the PNN classification mechanism is not given here since it is not the main purpose of this paper. The final number of classified and unclassified vehicular records generated through the two-phases of classification is shown in Table 1 along with the traffic parameters for each year of the study period. For instance, in Table 1, 12,828,708 gives a final number of vehicular records classified into 13 classes and 805 gives a final number of vehicular records unclassified for the entire 5 study years. The unclassified records were distributed to each of the vehicle classes according to the ratio of each class to total vehicle numbers. Subsequently, the 13 classified vehicle classes are aggregated into four vehicle classes such as passenger cars and three major truck types, namely straight unit truck, single trailer and multi trailer unit. All classification procedures for both FHWA scheme “F” and PNN were performed by computer codes developed using Visual Basic application (VBA).
As described in introduction, two analyses scaled by micro- and macro-level were conducted to investigate the impact of weather conditions on truck type distribution. Specifically for an analysis in microscopic level, temperature is aggregated with 7 categories, namely baseline (over 0 °C), CC1 (− 5 – 0 °C), CC2 (− 10 – − 5 °C), CC3 (− 15 – − 10 °C), CC4 (− 20 – − 15 °C), CC5 (− 25 – − 20 °C) and CC6 (below − 25 °C) with 5 °C equal interval. Snowfall is aggregated with 3 snowfall categories, namely SC1 (SC1 = 0 cm), SC2 (0 < SC2 ≤ 3 cm) and SC3 (SC3 > 3 cm). For all these purposes, historical weather data obtained from the Environment Canada Climate Database [17] for study period were utilized along with WIM traffic data.
As an intuitive analysis before conducting the proposed combined statistical tests, it is worthwhile to see how truck type distributions are varied monthly and seasonally in collected data. For pursuing this, daily truck traffic volumes of 5 years for each of the truck types are plotted in Fig. 1. Black line represents straight unit truck, which shows the highest volumes in the study site. Red line represents the variation pattern of single trailer unit, and blue line represents multi trailer unit, which is the lowest truck volumes. A bold solid line representing each type of trucks is provided in the same figure to show average travel patterns of 5 years. The day and month are displayed on the x-axis. All types of trucks have fewer runs over the weekend. It is also observed that the distribution of the truck type fluctuates throughout the year associated with the temporal change in the month and season. Furthermore, to see whether there is observable impact of inclement weather factors such as snowfall and temperature on truck type distribution patterns during winter season is another intuitive analysis conducted. The relationship between inclement weather factors and the variations in truck type distribution is depicted for the year 2009 in Fig. 2 using truck traffic and weather data. The exact date of observation is displayed on the x-axis using a naming convention of 091201, where 09 means 2009, 12 means December, and 01 means first day of the month. Truck traffic is slightly out of normal traffic volume between 091201 and 091228, where heavy snowfall (16 cm) and cold temperatures (below − 25 °C) are distributed. However, the problem is that it is not possible to confirm whether or not there are significant changes in truck type distribution only by visual inspection.
In order to ensure the legitimacy of applying nonparametric tests, normality test for the data set is also conducted to decide whether or not nonparametric test is fit well for this study. The test involves composing 30 data sets (5 years of data sets for two different level analyses for three truck types) and computing the normality of each data set with Anderson–Darling test module available in R statistical computing software [21], and its results with p value are summarized in Table 2. For a data set with a p value greater than 0.05, the possibility that a sample will come from a normal distribution is higher. As a result, a total of 28 out of 30 sample data sets are more likely to come from the normal distribution, and the other two data sets are not. This normality test results showed that all study data did not always obey the normal distribution. Therefore, an alternative test such as nonparametric method for which validity does not depend on rigid assumptions can be considered [6, 22]. The nonparametric test procedures met the needs of this study, since they are valid under very general assumptions and no normality is required [23]. Therefore, it is valid that Chi-squared test combined with binomial test is applicable for the study data sets.
5 Macroscopic impact analysis of month and season on variations of truck type distribution
Because of its geographical location, winter weather conditions in Canada are very poor. Sometimes extreme weather conditions such as heavy snowfall, blizzards, temperature below − 35 °C, freezing rain and high wind chills are often seen. These meteorological conditions are often observed in winter (months and season) and may be factors causing significant variations in highway traffic patterns. Three statistical methods were gradually adopted to investigate the changes in the distribution of truck types with monthly time variations. First, the WIM data were classified into 13 vehicle classes using the vehicle classification method and then aggregate all truck traffic into three major truck types: straight unit truck, single trailer and multi trailer unit. The average daily truck traffic per month was calculated for each of the three truck types. This is called observed truck type distribution pattern (OTTDP). This pattern is compared through statistical analysis with expected truck type distribution pattern (ETTDP) that is calculated based on the proposed null hypothesis. The null hypothesis \( (H_{0} ) \) proposed is that average daily traffic distribution patterns of trucks per month remained stable irrespective of month. Second, a Chi-squared \( (\chi^{2} ) \) test, a widely used goodness-of-fit test, was applied to see whether there are changes in the distribution pattern of truck types with month [23]. If the two truck type distribution patterns are similar to each other, a match between the observed truck type distribution pattern and the expected truck type distribution pattern is expected and thus the null hypothesis cannot be rejected. Third, the Binomial Probability (BP) test was applied to confirm the statistical significance of the entire study period by using the Chi-squared results that were repeated five times according to the study period. Assumption applied in the BP test is that the result of the Chi-squared test for the specific year turns out to be a significance (reject \( H_{0} \)) or not significance (accept \( H_{0} \)). Therefore, the test result for the specific year can be considered to comply with a binomial distribution with a parameter of success probability (p) of 0.5. As a result, it is possible to confirm at 95% confidence level whether the truck type distribution changes significantly with monthly using the 5-year Chi-squared test results that obey to the binomial probability distribution.
To help better understand the methodology described in the previous section, a sample calculation using 2005 truck traffic data was provided. The observed truck type distribution patterns for each truck type are shown in Table 3. The traffic volume for each cell in Table 3 is calculated using the following equation:
where \( i \) is the study year from 2005 to 2009, \( j \) is truck types considered, straight unit truck, single trailer, and multi trailer unit, \( k \) is the months in the year (Jan, Feb, Mar, Apr, May, Jun, Jul, …, Dec), \( \text{ND}_{ik} \) is the number of days for the year \( i \) and the month \( k \), and \( \text{DT}_{ijk} \) is daily truck traffic volumes for the year \( i \) and truck type \( j \) and month \( k \).
To perform the Chi-squared test, the ETTDP table should be also prepared in the same matrix format with the OTTDP table. The ETTDP table can be prepared based on the null hypothesis (\( H_{0} \)) that the truck type distribution does not change over the months. The null hypothesis can be expressed in the following mathematical relation:
where \( n_{j.} \) is marginal grand total for each truck type \( j \) and \( n_{.k} \) is marginal grand total for each month \( k \), and \( n \) represents a grand total in Table 4. The expected distribution pattern calculated with Eq. (2) at the sample site for the year 2005 is presented in Table 4. A total of 10 matrix tables, two matrix tables for each year of 5 years, are prepared to conduct Chi-squared test for the 5-year study period.
Based on the two types of truck distribution patterns as listed in Tables 3 and 4 for the year 2005, a Chi-squared test statistic can be calculated using the Eq. (3). The test statistic for this sample year is 241.23.
A critical Chi-squared value calculated at the significance level of α = 0.05 and the 22 degrees of freedom is 34.92. As described in Fig. 3, the null hypothesis is rejected because the test statistic of 241.23 is larger than the threshold statistic of 34.92, falling in the denial zone. In other words, it is significant that the truck type distribution pattern changes over months in the specific year of 2005 for the Leduc study site. The same statistical test was repeatedly performed for the remaining 4 years, and the results are summarized in Table 5.
A binomial probability test was applied to the 5-year Chi-squared test results to arrive at comprehensive conclusion for the entire data. The fact that the truck type distribution pattern varies by month was observed for only 3 out of 5 years. According to the binomial probability distribution in Fig. 4, the threshold value of the binomial test at 0.05 significance level for trial with 5 attempts and 0.5 success probability is 4 successes out of 5 attempts. Therefore, according to the results of combining Chi-squared and binomial tests, no change in the truck type distribution pattern was observed in statistical terms for the Leduc site during the 5-year study period from 2005 to 2009. In other words, it seems that, in the intuitive analysis of study data as depicted in Figs. 1 and 2, the number and distribution of each truck type included in the mixed traffic flow at the study site varies monthly and seasonally and also varies with various colds and snowfall. It is statistically verified from study results that the proportions of each truck type in the traffic stream at the study site remained stable month to month and season to season. Figure 5 shows graphically traffic patterns of the observed truck type distribution and expected truck type distribution used for combined statistical analysis over a 5-year period.
Observed truck type distribution and expected truck type distribution patterns over a 5-year period. a Truck type distribution for 2005 (dependent). b Truck type distribution for 2006 (independent). c Truck type distribution for 2007 (dependent). d Truck type distribution for 2008 (dependent). e Truck type distribution for 2009 (independent)
It would be preferable to know which months play a key role for the years such as 2005, 2007 and 2008 where the truck type distribution varies month to month. To do this, the Chi-squared goodness-of-fit test was conducted by comparing the observed tuck type distribution for the specific month to the expected truck type distribution, which is averaged truck traffic volume over the year. Table 6 illustrates the observed truck type distribution for months \( (O_{2005jk} ) \) and the expected truck type distribution averaged over the year 2005 \( (E_{2005j} ) \).
To test whether or not the observed truck type distribution in January is similar to the expected truck type distribution in 2005, the Chi-squared test statistic is calculated using Eq. (4):
where \( \chi_{2005k}^{2} \) is the Chi-squared test statistic for the specific month \( k\left( { = {\text{January}}} \right) \) in the year 2005, \( O_{2005jk} \) is the observed truck volume for truck type \( j \) for specific month \( k \) in the year 2005, and \( E_{2005j} \) is the expected truck volume for truck type \( j \) over the year 2005. In the sample test for January, the \( \chi^{2} \) test statistic is calculated as 4.25 and the critical Chi-squared value is 5.99 for 2 degrees of freedom at 0.05 significance level as depicted graphically in Fig. 6. Since the test statistic value of 4.25 is smaller than the critical value of 5.99, there is not enough evidence to reject the null hypothesis. It is significant to indicate that the observed truck type distribution of January is similar to the expected truck type distribution in the year 2005 for Leduc study site. The same analysis is conducted repeatedly sixty times for all months included in 5-year study period, and the results are summarized in Table 7.
It is indicated that 8 months (i.e., Apr–Jun, Aug–Dec) play a key role in making variations in truck type distribution for the year 2005. For the year 2007, 5 months (i.e., Feb, Jun, Sept, Oct, Dec) and for the year 2008, 6 months (i.e., Jan, Apr, Jun, Sept, Oct, Dec) are also identified as contributing months, respectively. The variation of the truck type distribution by month can be clearly observed by checking the physical distance between two distribution patterns for the years 2005, 2007 and 2008 through Fig. 5a, c, d, respectively, and the variation is statistically verified through this statistical test.
In the following section, the month of the year is divided into two seasons, winter and non-winter, and the statistical significance of the seasonal variation of the truck traffic pattern is investigated. This section compares and analyzes the distribution patterns of truck types between winter and non-winter (or summer) seasons. Based on weather data from Environment Canada Climate Database (ECCD 2010), the months from November to March are categorized as winter season with severe snow and cold temperatures, and the remaining months are classified as non-winter season.
The observed average daily truck type distribution and its expected value are summarized in Table 8 for winter and non-winter seasons for the year 2005 as an example.
The calculated Chi-squared test statistic is 8.71, and the threshold for the Chi-squared test is 5.99 for two degrees of freedom at a significance level of 0.05. Since 8.71 is greater than 5.99, the hypothesis that truck type distribution is same between seasons, winter and non-winter, is rejected in the 2005 example. The same statistical analysis was repeated for the remaining 4 years, and the results are summarized in Table 9.
The binomial tests were performed using the results of the 5-year Chi-squared test to arrive at a comprehensive conclusion on all data. As a result, seasonal change in the truck type distribution pattern at the Leduc site during the 5-year study period was not statistically observed. It is statistically indicated that the truck type distribution remains stable even in severe winter weather conditions.
Seasonal changes in truck type distribution can also be verified by comparing the average truck type distribution for each season with the yearly expected truck type distribution. Table 10 shows the truck type distribution for each season and the expected truck type distribution for the year 2005. Table 11 shows the goodness-of-fit test results for truck type distribution in winter season compared to the expected truck type distribution using the 5-year study period.
Table 11 shows that there is no reason to reject the hypothesis that the distribution of truck type during the winter season is the same as the expected truck type distribution for 5 years. The variation in truck type distribution was not observed in the same analysis extended to the non-winter as well. Table 12 shows the Chi-squared goodness-of-fit test results for the two seasonal groups. The number of significant (or rejected) years is “0” for all seasonal groups. The truck type distribution maintains a stable distribution regardless of the season. It is the same analysis results as the previous section.
6 Microscopic impact analysis of cold on truck type distribution
This section uses only the traffic data collected in winter season to microscopically examine the impact of cold and snow on the truck type distribution pattern. The months of November–March were classified as winter season in Canada. A total number of 490 days was sampled from 5 years of study period. And then the 490 days are categorized into 7 cold categories based on the daily average temperature. The next step is to conduct a calculation of the average daily traffic volume for each type of trucks traveling in each cold category. The 7 cold categories with a 5 °C equal interval are: baseline (over 0 °C), CC1 (− 5 – 0 °C), CC2 (− 10 – − 5 °C), CC3 (− 15 – − 10 °C), CC4 (− 20 – − 15 °C), CC5 (− 25 – − 20 °C) and CC6 (below − 25 °C). Table 13 is prepared for Chi-squared test, and Table 14 summarizes the Chi-squared test results for all study years to arrive at comprehensive conclusion on the effect of cold on the truck type distribution pattern through the binomial test.
The test Chi-squared statistic calculated from Table 13 for the year 2005 is 5.53, and the critical Chi-squared value searched in Fig. 7 is 21.03 for 12 degrees of freedom at the significance level of 0.05. Since 5.53 is less than 21.03, the null hypothesis cannot be rejected. It is statistically indicated that truck type distribution pattern does not change over between cold categories for the year 2005.
Test results of all 5 years are presented in Table 14. The results show that the truck type distribution is affected by the cold only for 2 years (i.e., 2006 and 2008) out of the five test years. In conclusion, the distribution of truck types is not affected by severe cold weather even in winter season.
The impact of cold on truck type distribution can also be tested by comparing the average truck type distribution \( \left( j \right) \) for each cold category \( \left( k \right) \) represented by \( (O_{2005jk} ) \), with the truck type distribution expected in winter season represented by \( (E_{2005j} ) \). Table 15 shows the truck type distribution for each cold category and the expected truck type distribution throughout the winter season for the year of 2005 regardless of the severity of cold. Table 17 shows the goodness-of-fit test results for truck type distribution for baseline cold category compared to the expected truck type distribution during the 5-year study period using Eq. (4).
Test results in Table 16(a) show that truck type distribution for baseline cold category is similar to the expected truck type distribution pattern. Table 16(b) shows all test results for all 7 cold categories for 5-year study period. None of truck type distribution under 7 cold categories is varied much from the expected truck type distribution pattern measured in winter season (490 days). It is again verified that truck type distribution is not affected by severe cold weather in winter season and stays in stable condition.
7 Microscopic impact analysis of snowfall on truck type distribution
Snowfall is an important factor affecting variations of traffic volumes in winter season. In the research conducted by Roh et al. [24, 25], it is indicated through regression modeling techniques that traffic volumes for both passenger cars and truck decrease with an increase in the amount of snowfall on the ground for regional long-distance-type road facilities. However, interestingly, it is also indicated that truck traffic volumes on the commuter-type road are not greatly affected as much as those of long-distance-type road. The current research confirms the results in the previous studies [24, 25] on the variations of truck traffic volumes in winter season on the commuter road.
As mentioned in the previous section, 490 days are sampled from the months of November to March for the 5-year study period to collect the records of snowfall. The amount of snowfalls varies widely ranging from 0 to 16.2 cm. The snowfall is aggregated with 3 levels: SC1 (SC = 0 cm), SC2 (0 < SC ≤ 3 cm) and SC3 (SC > 3 cm) considering snowfall frequency and amount. As a sample calculation, the observed and expected truck type distributions with respect to 3 snowfall levels for the year 2005 are given in Table 17.
The Chi-squared test statistic is calculated out to be 1.19 from the Table 17, as depicted in Fig. 8, the critical value is located at 9.49 for given 4 degrees of freedom at 0.05 significance level. Since 1.19 is less than 9.49 and p value is greater than 0.05, falling in non-rejection region, null hypothesis is accepted. It is significant with 95% confidence to say that snowfall is not a factor causing variations on truck type distribution for the year 2005 in Leduc study site.
A comprehensive conclusion for all 5 years is drawn from Table 18 using binomial test. Truck type distribution remained stable, not affected by any amount of snowfall even in winter season, specifically, for this kind of commuter-type road facility.
The impact of each snowfall category on truck type distribution can be verified by comparing the average truck type distribution \( \left( j \right) \) for each snowfall category \( \left( k \right) \) represented by \( (O_{2005jk} ) \), with the truck type distribution expected in any amounts of snowfall in winter season represented by \( (E_{2005j} ) \). Table 19 shows the truck type distribution for each snowfall category and the expected truck type distribution throughout the winter season for the year of 2005 irrespective of the amount of snowfall. Table 20 (a) shows the goodness-of-fit test results for truck type distribution for the most severe snowfall category SC3 compared to the expected truck type distribution during the 5-year study period using Eq. (4).
Test results in Table 20(a) show that truck type distribution for SC3 snowfall category is similar to the expected truck type distribution pattern. Table 20(b) shows all test results for all 3 snowfall categories for 5-year study period. None of truck type distribution under 3 snowfall categories is varied much from the expected truck type distribution pattern measured in winter season (490 days). It is indicated that truck type distribution is not affected by the amount of snowfall on the ground in winter season and stays in stable condition.
8 Summary and conclusions
It has been clearly indicated in many of the studies conducted in the past that the weather conditions are major factors affecting variations of traffic volumes in highway. However, previous studies in this area have been limited to studies using only total traffic volume, and even studies on truck traffic have considered only the total truck traffic volume. Understanding the patterns of truck type distribution in severe weather conditions during the winter can provide valuable insights to extend the truck monitoring program, which is usually conducted during the summer, to winter. An investigation of the impact of months and seasons (i.e., winter vs. non-winter) on the variations of truck type distribution was presented as macro-level analysis. Micro-level analysis was further carried out to investigate the impact of severe weather conditions (i.e., snowfall and temperature) on the variations of truck type distribution as well, specifically for the winter season. Five-year weigh-in-motion (WIM) data were collected from Highway 2A site located south of the City of Leduc in Alberta, Canada. Three truck types, namely straight unit truck, single trailer and multi trailer unit, have been classified based on information on axle number and spacing.
This paper focuses on the method of using nonparametric analysis method in truck traffic data analysis, which has a few related studies. In addition, the parametric method can be easily applied as an analytical technique. In fact, it is revealed through regression modeling method that the total truck traffic volume was not significantly affected by winter weather conditions compared to passenger car traffic in several studies [3, 5, 24, 25]. Therefore, the nonparametric modeling results presented in this study seem to be consistent with the parametric modeling results obtained in previous studies. The use of truck type distribution patterns in the analysis of the impact of winter weather conditions on the variations of truck traffic volumes is a contributing part of this study.
In the preliminary analysis of study data as depicted in Figs. 1 and 2, the number and distribution of each truck type included in the mixed traffic flow at the study site varies monthly and seasonally and also varies with various colds and snowfall. However, the results of combined Chi-squared and binomial statistical significance tests indicated that the truck type distribution was not related to the months (or seasons) and, furthermore, was not affected by the inclement winter weather conditions such as severe cold and snowfall. In other words, the proportion of each truck type in the mixed truck traffic, i.e., straight unit truck, single trailer and multi trailer unit, remained essentially stable at the Leduc study site during the 5-year study period from 2005 to 2009. The results of this study show that there is ample evidence that a sustainable truck traffic counting program can be planned throughout the year. For example, the short-duration truck traffic count for periods ranging from a few days to several weeks but less than a month can be carried out even during winter seasons to get reasonably good estimates of transportation parameters such as truck annual average daily traffic (TAADT). However, in order to actually apply the study results in estimating precise truck traffic parameters, in-depth research on “what is the optimal schedule and duration” should be conducted for all periods of the year, including the winter period.
To confirm the findings of this study and to compare the characteristics of truck traffic on other highways, further studies are underway using other WIM sites installed on highways that are used for a variety of purposes other than commuting. Consequently, it becomes possible to design truck traffic monitoring programs optimized for various types of highway facilities in terms of counting frequency and duration, which further can be performed throughout the year for efficiently operating the resources allocated.
References
Robert H, Emily S, Daniel K, Hesham R, Mohamadreza F (2006) Empirical studies on traffic flow in inclement weather. FHWA, U.S. Department of Transportation
Sandeep D, Satish S (2008) Impact of cold and snow on temporal and spatial variations of highway traffic volumes. J Transp Geogr 16(5):358–372. https://doi.org/10.1016/j.jtrangeo.2007.12.003
Hyuk-Jae R, Satish S, Sandeep D (2014) The impact of cold and snow on weekday and weekend highway total and passenger cars traffic volumes. Open Transp J 8:62–72. https://doi.org/10.2174/1874447801408010062
FHWA (2001) Traffic monitoring guide. U.S. Department of Transportation Federal Highway Administration Office of Highway Policy Information
Hyuk-Jae R, Sandeep D, Satish S (2012) Impact of severe winter conditions on highway truck traffic. In: 9th International Transportation Specialty CSCE Annual Conference, Edmonton, Alberta, Canada
Zhaobin L (2006) Study of highway traffic peaking due to statutory holidays. Dissertation, University of Regina
Rashad MH, David AK (1993) Traffic volume reduction due to winter storm conditions. J Transp Res Board 1387:159–164
Al Hassan Y, Derek JB (1999) The impact of unseasonable or extreme weather on traffic activity within lothian region, Scotland. J Transp Geogr 7:209–213. https://doi.org/10.1016/S0966-6923(98)00047-7
Keith K, Leland S (2000) Winter storm event volume impact analysis using multiple-source archived monitoring data. J Transp Res Board 1700:10–16. https://doi.org/10.3141/1700-03
Kevin K, Ian S (2005) The association of rainfall and other weather variables with road traffic volume in Melbourne, Australia. Accid Anal Prev 37:109–124. https://doi.org/10.1016/j.aap.2004.07.005
James C, Li Z, John H (2003) Identifying and assessing key weather-related parameters and their impacts on traffic operations using simulation. In: 73th Annual Meeting of Institute of Transportation Engineers, Washington, DC
Pamela JM (1999) Adverse weather traffic signal timing. In: 69th Annual Meeting of Institute of Transportation Engineers, Las Vegas
Markku K, Heikki S (2007) Effects of weather and weather forecasts on driver behavior. Transp Res Part F 10:288–299. https://doi.org/10.1016/j.trf.2006.11.002
Thomas M, Manish A, Garrett B (2006) Whether weather matters to traffic demand, traffic Safety, and traffic operations and flow. J Transp Res Board 1948:170–176. https://doi.org/10.3141/1948-19
Stanley AC (1996) Effects of summer precipitation on urban transportation. Clim Change 32:481–495. https://doi.org/10.1007/BF00140357
Peter K (2008) Alberta infrastructure and transportation weigh in motion report. Alberta Transportation
ECCD (2010) Environment Canada’s Climate Database. Gatineau, Quebec, Canada. www.climate.weatheroffice.gc.ca/climateData/canada_e.html. Accessed 20 May 2014
ArcGIS 10 (2010) Environmental system research institute, ArcGIS 10 help library, Redlands, California
John HW, Gary AB, Robert IS (1985) Field evaluation of FHWA vehicle classification categories. FHWA, U.S. Department of Transportation
Renatus M, Valerian K, Majura S (2006) Probabilistic neural networks application for vehicle classification. J Transp Eng 132:293–302. https://doi.org/10.1061/(ASCE)0733-947X(2006)132:4(293)
RFSC (2010) R Development Core Team: a language and environment for statistical computing. R Foundation for Statistical Computing, Vienna
Hyuk-Jae R, Satish S (2017) Combined nonparametric Chi squared and binomial statistical test on truck traffic volume changes in Canadian provincial highway network. Transport (forthcoming)
Wayne WD (1990) Applied nonparametric statistics, 2nd edn. PWS-KENT Publishing Company, Boston
Hyuk-Jae R, Satish S, Prasant S (2016) Modeling snow and cold effects for classified highway traffic volume. KSCE J Civ Eng 20:1514–1525. https://doi.org/10.1007/s12205-015-0236-0
Hyuk-Jae R, Prasant S, Satish S, Sandeep D, Babak M (2016) Statistical investigations of snowfall and temperature with passenger car and truck traffic on primary highway in Canada. J Cold Regions Eng. https://doi.org/10.1061/(ASCE)CR.1943-5495.0000099
Acknowledgements
The author is grateful toward the Natural Science and Engineering Research Council of Canada (NSERC) and Saskatchewan Government Insurance (SGI) for their financial support. The author also thanks Alberta Transportation for providing the WIM data used in this study. It is also acknowledged that the portion of this paper is taken from the conference paper presented in the 12th Transportation Planning and Implementation Methodologies for Developing Countries.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Roh, HJ., Sharma, S. Microscopic and macroscopic diagnosis of the effect of winter weather conditions on distribution pattern of truck types in regional commuter road. J. Mod. Transport. 26, 57–71 (2018). https://doi.org/10.1007/s40534-017-0153-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40534-017-0153-7