1 Introduction

Precast deck panels are capable of improving durability and quality of the deck thorough casting in a controlled environment. Full-depth precast deck panels are usually developed for accelerating bridge construction. Use of these panels to bridge construction has gained wide acceptance because they can offer several advantages such as rapid construction, minimal onsite formwork and scaffolding, reduced labor and structural costs, and improved quality and durability [1–4]. In addition, these bridge decks may require lower maintenance and life-cycle costs [5].

Currently, full-depth precast deck panels are connected to supporting girders through shear pockets. Void spaces are placed within the precast panels when they are fabricated at the prestressing yard. When full-depth precast deck panels are transported and installed at the construction site, shear pockets are aligned with the mechanical shear connectors of the supporting beam and set in place. The shear pockets are generally through the panel thickness. However, the opening for shear studs could also be on the bottom side only, allowing smoother riding surface. After placement, the pockets are filled with grout to connect deck panels to the supporting girders. An illustration of the current practice is shown in Fig. 1 [6]. Leveling bolts are also incorporated into precast deck panel, allowing the achievement of desired deck profile. Various transverse joint types have been utilized in practices [7, 8], such as match cast joints with shear keys, and joints with mild or post-tensioned reinforcement. Field experiences indicate that achieving the final deck profile using “leveling bolts,” in general, is an easy task.

Fig. 1
figure 1

Full-depth precast deck panel system

Full size image

However, there are still two issues associated with the current practice that should be investigated to enhance the constructability of bridge superstructures with full-depth precast deck panels. First, in the current practice, grouting is usually required to fill both shear pockets and the “haunch”—the interstice between the panel and supporting beam. Such practice can be difficult in practice because quality control inspections and repair require access to the underside of the bridge deck after grouting. Consequently, researchers have reported that void spaces exist between supporting girders and deck panels after grouting even in laboratories [7, 9]. The connection between precast deck panel and supporting girder is a field operation and as such should not compromise the durability and result in service life reduction. Second, the maximum spacing for shear connectors is 60.96 cm as stipulated by AASHTO LRFD Specifications [10]. Badie and Tadros [7] reported that a very limited amount of testing was conducted with stud spacing greater than 60.96 cm. In addition, the majority of these tests were made for cast-in-place (CIP) slabs, where the studs are uniformly spaced across the specimen and not clustered in groups, as is the case with precast panel construction.

In order to deal with these weaknesses, an innovative deck panel shown in Fig. 2 was proposed. In the proposed system, the deck panels were connected to the girder by the discrete shear connections. Different to traditional deck panels, the proposed system improved the connection by fully connection strips with bigger spacing in transverse direction. As a result, the increased spacing of connectors and ungrouted haunches would be developed. On one hand, to minimize the number of the shear pockets in the proposed system, the shear connectors are grouped in clusters and spaced within the transverse panel joint. As a result, a large shear capacity will be obtained at these discrete locations. In addition, when the stud connections were originally developed for composite girder, most slabs, particularly within buildings, do not require a haunch between the slab and the girder. On the other hand, the haunch in the proposed system will not be grouted between the shear connectors, and the slab and the beam will behave differently when compared to those of the traditional composite system. The deck panels deflect between the shear connectors, and therefore the grouted connectors act as short “column” subjected to an axial load and bending moments. The concrete in the miniature columns may experience high stresses due to end rotation and the eccentricity of the applied load. Thus, the behavior of the miniature columns, subjected to a combined axial load, shear, and bending moment (Fig. 2), is essential to the capability of the shear connector to perform satisfactorily in the proposed system (i.e., a similar capacity predicted by previous research for beams and decks designed with full composite action).

Fig. 2
figure 2

Schematic of force transfer in grouted connectors’ region

Full size image

Traditional bridge decks continuously supported by girders are designed to resist one-way bending and are considered as continuous beams in the transverse direction. Bridge girders act as the support for the continuous beams. In Fig. 3, bridge girders do not provide continuous support as gaps exist between the deck panels and the bridge girders. The precast deck panels are supported by the discrete shear connectors; therefore, they do not behave as one-way slabs as those in traditional deck systems. Instead, these deck panels are more comparable to two-way flat plates in buildings. Therefore, the design of precast deck panels in this system should be reevaluated. Specifically, the condition under which the precast deck panels may be treated as two-way slabs or one-way slabs should be studied.

Fig. 3
figure 3

Proposed shear connection of deck panels and girders (plan view)

Full size image

These critical issues will be addressed in the proposed project through numerical analyses. Investigation of the methodologies developed in the past and current applications of full-depth panels in the Unites States and around the world, and the current construction practices will be studied. Then the key parameters relevant to each identified issue will be identified as well as the punching shear failure.

The design procedures for the bridge girders in the proposed deck system should be reevaluated, including the impact of the gap (similar to a small “web opening” at the juncture of deck and girder top flange) on vertical shear resistance, load distribution factors, dynamic allowance factors, and effective flange width.

This paper introduces a simplified full-depth precast concrete deck panel system for accelerating bridge construction. In addition to the introductory section, this paper consists of four other sections. Section 2 introduces the concept of simplified full-depth precast concrete deck system and its practice. Section 3 analyzes the static response. Section 4 deals with the dynamic response. The last section summarizes some conclusions and discusses some issues for attention.

2 System description and current practice

A full-depth precast deck system employs a series of precast concrete panels that are full depth in thickness—as required by structural design—with the length and width determined by specific geometry. The length of the panel along the roadway is typically 244–366 cm. The width of the panels can be equal to the width of the bridge; both panel dimensions are typically determined by transportation considerations. The general preference of precast component manufacturers and bridge contractors is to use prestressed concrete panels to alleviate cracking potential from transportation and handling. Historically, the design of an effective full-depth precast bridge deck system consisted of the following:

  • precast panels with pockets or block-outs to accommodate girder to panel shear connections;

  • allowance for grouting between the supporting girder and the precast panel;

  • temporary support and forms along the girder to retain grout;

  • transverse joints detailing between panels; and

  • an overlay system to improve the rideability.

The proposed example new deck concept is further illustrated in Fig. 4 for both steel and prestressed concrete superstructures. Note that the deflection of the steel girder and the camber of the prestressed concrete girder are magnified to demonstrate the idea. In the new deck system, the precast concrete deck panels are supported on the girders only at the transverse connections on the top of the girder.

Fig. 4
figure 4

New precast deck system with steel and prestressed concrete girders

Full size image

The following behavioral considerations have been identified regarding the use of the new precast deck system:

  1. (1)

    The concrete decks are currently treated as one-way slabs supported by the girders in traditional deck systems, while the decks in the new system are two-way slabs supported by the grouted connections with variable haunches (acting as discrete short columns). The analysis, design, and construction of the deck panels thus need to be updated.

  2. (2)

    The transverse connections for full-depth precast deck systems have been well developed through previous research, especially through the NCHRP Project 10–71 [8]. However, the two-way actions in the deck panels of the new system cause negative bending moments at the transverse connections, especially near the supports on the top of the girders. The well-developed transverse connections may need to be updated to accommodate the negative moments [11].

  3. (3)

    The two-way actions in the deck panels may also create bending moments along the longitudinal connections. The well-developed longitudinal connections through NCHRP Project 10–71 may need to be checked for the differences in the internal forces near the connections [12].

  4. (4)

    A large length of the deck panels is desirable to facilitate the fabrication and installation of the deck panels. The elimination of the intermediate shear pockets poses a challenge to the design of horizontal stud connections to ensure full/partial composite action. Specifically, stud groups at a large distance (e.g., up to 244 cm) may not be able to provide the same shear transferring mechanism and capacity as that provided by the continuous grouted haunches with studs spaced traditionally 30.48–60.96 cm.

It may be viable for the bridge design to rely on full composite action under the service loading while only partial composite actions at the ultimate limit state. The design assumption should be verified.

The static response and dynamic response of the traditional full-depth precast concrete deck panel systems and the new full-depth precast deck panel system were investigated by finite element method (FEM), and compared to each other in sequent sections.

3 Static response

In the static analysis, the bridge models were established using ABAQUS. The load distribution factor, the effective slab width, and the force/moment distribution in the slab were investigated.

The bridge shown in Fig. 5 was considered and analyzed using the FEM for static evaluation.

Fig. 5
figure 5

Cross section of concrete girder–concrete deck bridge [13]

Full size image

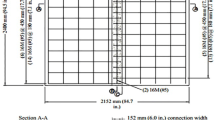
The span of the bridge for this model was 18.3 m, and a 19-cm-thick concrete deck panel was supported on the AASHTO Type III girders, as shown in Fig. 5. A haunch of 127 cm was included in the analysis. The spacing of the discrete connectors connecting the girders and the deck panel was 122 cm. As shown in Fig. 6, a tri-axle, HS20-44 truck with tire loadings of 35, 145, and 145 kN was used as the static loading for this analysis. In the longitudinal direction, the mid-wheels were located directly above the mid-span of the girders. In the transverse direction, the truck was symmetrically loaded on the middle girder.

Fig. 6
figure 6

HS20-44 truck [13]

Full size image

Two different systems were compared: a FE model of the conventional deck system (no haunch gap) and a deck system supported only at discrete locations. The defected contour shapes for both of these models are presented in Figs. 7 and 8. In the model, the two surfaces of the girders and the deck panel are tied together to simulate the fully composite action at the interface.

Fig. 7
figure 7

Deflected shape with discrete connectors at 122 cm

Full size image
Fig. 8
figure 8

Deflected shape with slab fully supported on beam

Full size image

The shapes of the deflection contour for both systems are very similar; however, the results tabulated in Table 1 reveal that the mid-span deflection of the middle girder containing discrete connections at 122 cm is approximately 10 % larger than that in the fully supported model.

Table 1 Deflection of girders at mid-span (mm)
Full size table

In this static analysis, the load distribution factor (DF) was investigated and the results are shown in Fig. 9. It reveals that the middle girder (girder 3) will take the most truck load, while the side girder will not contribute much to resist the load in the case of the given load position. By comparison, the DF for two bridge deck systems is very close.

Fig. 9
figure 9

DF comparison of the two bridge models

Full size image

Also, the static response of the bridge slab was investigated by examining the normal stress distribution of the slab at the mid-span. The spacing between the left interior girder and the middle girder is 213 cm. The slab within this spacing was investigated, and the results are shown in Fig. 10. At the load position, the normal stress reaches the maximum tension stress, then gradually decreases, and finally changes to compression stress at the girder. Comparison reveals that the shapes of the normal stress distribution in both models are similar, although the peak tension stress using the discrete connector model is greater than that in the fully supported model, and the peak compression stress in the former model is smaller than that in the latter model.

Fig. 10
figure 10

Slab normal stress distribution between two interior girders

Full size image

The effective flange width (b e) of a flanged member was investigated by examining the normal stress distribution of the slab in between girders. This distribution is shown in Fig. 10. The effective flange width can be defined using Eq. (1). This equation captures the maximum normal stress and converts it into flange width based upon the normal stress distribution in the slab.

$$b_{\text{e}} = \frac{1}{{\sigma_{\hbox{max} } }}\int\limits_{y\,=\,0}^{b} {\sigma_{x} }\,{\text{d}}y ,$$
(1)

where b e is the effective flange width, b is the width of the flange, σ x is the normal stress in the flange, and σ max is the maximum normal stress in the flange.

At the mid-span, the total tension flange width of the discrete connector model is greater than that of the fully supported model, while the total compression flange width of the discrete connector model is smaller. By comparison, the effective tension flange width (the width of the green rectangle) of the discrete connector model is greater than that of the fully supported model; the effective compression flange width (the width of the purple rectangle) of the discrete connector model is significantly smaller than that of the fully supported model.

The force and moment in the panel were also analyzed. The definitions of forces/moments within the shell element in ABAQUS are as follows:

SF1—direct membrane force per unit width in local 1-direction (x-axis);

SF2—direct membrane force per unit width in local 2-direction (z-axis);

SM1—bending moment force per unit width about local 2-axis (z-axis);

SM2—bending moment force per unit width about local 1-axis (x-axis).

These forces and moments can be calculated as follows:

$$\left( {{\text{SF}}1,{\text{SF}}2} \right) = \int_{{ - \frac{{h}}{2}\,-\,{z_{\text{o}}} }}^{{\frac{h}{2}\,-\,{z_{\text{o}} }}} {\left( {\sigma_{11} ,\sigma_{22} } \right)}\,{\text{d}}z ,$$
(2)
$$\left( {{\text{SM1}},{\text{SM}}2} \right) = \int_{{ - \frac{{h}}{2}\,-\,{z_{\text{o}}} }}^{{\frac{h}{2}\,-\,{z_{\text{o}} }}} {\left( {\sigma_{11} ,\sigma_{22} } \right)}\,{{z\,d}}z ,$$
(3)

where z o is the offset of the reference surface from the mid-surface, h is the depth of the slab, σ 11 is the normal stress in 1-direction (x-axis), σ 22 is the normal stress in 2-direction (z-axis), and z is the distance from the reference surface.

In these FE models, the offset was zero. The locations and directions of SF1, SF2, SM1, and SM2 are shown in Fig. 11. If the slab is designed as a one-way slab model, SM1 is considered because the spacing of the girders is the length of each single span of the slab.

Fig. 11
figure 11

Location and direction of the slab force/moment

Full size image

The typical slab force/moment contours are shown in Figs. 12, 13 and 14. In the contours for the discrete connector model, the locations of the connection to the girder and deck panel are shown as the dented rectangular shell elements. By comparison of the slab force/moment distributions, the difference between the two bridge deck systems is revealed. Comparison of the maximum responses of the slab in the two deck systems is shown in Table 2. It is shown that the difference of maximum responses is more than 10 % for most parameters except the bending moment along the longitudinal direction (SM1). Note that the slab longitudinal compression (SF2) differs by approximately 80 %. Based upon this model, a larger deflection of the slab is expected for the new full-depth precast concrete deck panel system. The bending moment along the transverse direction SM2 in the new system is approximately 10 % higher than that in the conventional fully supported system; therefore, SM2 must be considered although it is ignored in the one-way slab design. For safety consideration of design of a real structure, increasing panel thickness and reducing spacing of shear connectors would be suggested to reduce the deflection and the interior forces.

Fig. 12
figure 12

Transverse force SF1 in the slab. a Discrete connector model—connectors at 122 cm. b Fully supported model

Full size image
Fig. 13
figure 13

Longitudinal force SF2 in the slab. a Discrete connector model—connectors at 122 cm. b Fully supported model

Full size image
Fig. 14
figure 14

Moment along the longitudinal direction SM1 in the slab. a Discrete connector model—connectors at 122 cm. b Fully supported model

Full size image
Table 2 Maximum responses of the slab in the two deck systems
Full size table

4 Dynamic response

A steel girder–concrete deck bridge is analyzed by FEM. The span of the bridge is 18.288 m. A 19-cm-thick concrete deck panel is supported on the steel girders (W36 × 232). There is a 1.27-cm gap between the girders and the deck panel. The spacing of the connectors connecting the girders and the deck panel is 121.9 cm.

As shown in Fig. 15, a two-axle truck is considered as a moving load. The major parameters of the vehicle are shown in Table 3. The load position in the transverse direction is shown in Fig. 16. The speed of the vehicle is 20 m/s.

Fig. 15
figure 15

Vehicle model [14]

Full size image
Table 3 Major parameters of vehicle for IM analysis [14]
Full size table
Fig. 16
figure 16

Transverse position of the truck load in IM analysis

Full size image

A FE model of the bridge is established with ANSYS. Both the steel W-shape girders and the concrete slab are simulated by BEAM4. The interaction of the moving vehicle and bridge is considered using APDL in ANSYS. Three different models (fully supported model, connector@122 cm model, and connector@244 cm model) are investigated to study the effect of connector numbers/spacing on the dynamic response of the bridge deck system. In the connector@122 cm model, there are 611 nodes, 845 beam elements, and 80 connection elements which are used for the simulation of girder–deck connectors.

The time history of the dynamic response of each steel girder is analyzed. The impact factor is calculated with Eq. (4):

$$1 + \mu = \frac{{A_{\text{dyn}} }}{{A_{\text{st}} }},$$
(4)

where µ is the impact factor, A dyn is the maximum dynamic deflection at the mid-span, and A st is the maximum deflection at the mid-span under the corresponding static load.

Because the dynamic response of the side girder is significantly smaller than that of the interior girders, the impact factor for the side girder is not evaluated. The impact factor of the interior girders is about 10 %, as shown in Fig. 17. The impact factors in both the fully supported model and the connector@122 cm model are very close. For the middle girder (girder 3), the impact factor is about 13 % higher in the connector@244 cm model than that in the fully supported model. Thus, the spacing of the girder–deck connectors affects the dynamic response. When the spacing of connectors increases to 244 cm, the impact factor of the new full-depth precast concrete deck system will be different from that of the conventional deck system. The limit of connector spacing will help the full-depth precast concrete deck panel systems act similar to the fully supported model (conventional bridge deck system).

Fig. 17
figure 17

Impact factor of interior girders in three FE models

Full size image

5 Conclusion and discussion

A simplified full-depth precast deck panels is developed for accelerating bridge construction. The static response and dynamic response have been investigated by FEM and compared to the traditional full-depth precast deck panels. Some conclusions can be drawn from the analysis as follows:

  1. 1.

    The concrete decks in the new system act as two-way slabs supported by the grouted connections with variable haunches (acting as discrete short columns), which is a far cry from that of the traditional one-way slabs supported by the girders. The analysis, design, and construction of the deck panels thus need to be updated.

  2. 2.

    Due to the two-way actions in the deck panels of the new system, the negative bending moments at the transverse connections as well as the longitudinal connections, especially near the supports on the top of the girders, might be a problem for the traditional connections developed for full-depth precast deck systems. The well-developed transverse and longitudinal connections may need to be updated to accommodate the negative moments.

  3. 3.

    The load distribution factors of girders in two kinds of deck systems are close to each other. However, the longitudinal nominal stress at the mid-span increases a lot for the new deck system. And the effective flange width of the new deck system differs from that of the traditional deck system.

  4. 4.

    The dynamic analytical results show that the impact factor will increase significantly when the spacing of the girder–deck connections increases, suggesting that the spacing of connections might be limited to guarantee the dynamic response of the new deck system.

In addition to the concerns mentioned above, attentions also need to be paid to the following issues to facilitate the application of simplified full-depth precast concrete deck panel systems:

  1. 1.

    The deck panels are supported by short columns created by grouting the transverse connections on the top of the girders as shown in Fig. 4. Design concerns such as punching shear should be considered in the design of transverse connections similar to all other slab-on-column systems. The punching shear problem has been studied for a long time, and the fiber reinforcement concrete or shear reinforcement in punching shear zone are proved helpful to increase punching shear strength. The possibility of punching shear failure will be investigated in further studies. If these failure modes are deemed likely, then slab-on-column connection details will be optimized.

  2. 2.

    The elimination of gap grouting as illustrated in Fig. 4 also impacts the behavior and efficiency of the stud connection. The grout near the studs may crack, causing the combined shear, bending, and even tension in the studs, which has been shown to greatly reduce the rigidity and strength of the studs. The push-out tests of studs subjected to combined tension and shear, as well as stud cluster with haunch, are recommended to investigate the behavior of connections.

  3. 3.

    Impact of gap (small “web opening”) on vertical shear resistance needs to be investigated. As discussed earlier, the gap between discrete connector clusters might have an impact on the vertical shear resistance similar to beams with web openings. Thus, the test of small-scale reinforced T-beams with openings in shear-critical zone is suggested to research the effect of the following parameters: the distance of the opening to the beam edge, the length of the opening, and the height of the opening.

  4. 4.

    System behavior would change with the relative stiffness between the slab and beam. Parametric analysis is necessary to study the relationship between system behavior and the relative stiffness of the slab and beam.

  5. 5.

    Lateral torsional buckling concerns, concrete localized crushing effects, and steel localized yielding effects are essential for the full-depth precast deck panels. In the following studies, determinations will be made regarding the likelihood of buckling, crushing, and yielding problems associated with the full-depth precast deck panels. If these failure modes are deemed likely, then connection details will be optimized.