1 Introduction

With the rapid development of economy, steel bridges are widely used in transportation due to the advantages of light weight, convenient and fast construction, and large span, etc. Fatigue cracks often initiate in of welded joints for steel bridges under cyclic traffic loading. Fracture mechanics as a useful tool is widely taken to assess fatigue life according to the initial and the final crack sizes. The stress intensity factor is the most important parameter in fracture mechanics, and it can be described by the stress field of crack tip. Loading conditions, geometric shapes, and crack sizes and positions have effects on the stress intensity factor. In general, the stress intensity factor can be obtained by analytical method, numerical method, or test method [1]. Since the numerical method can consider the effects of various geometric shapes and complex loadings, it is widely used in fracture mechanics.

A large number of studies on the stress intensity factor of welded joints have been done by scholars using numerical methods [2–6]. Al-Mukhtar et al. [7] evaluated the stress intensity factor of load-carrying cruciform welded joints using 2D finite element method, considering the effects of weld size and plate thickness ratio. The results show that the weld size has a major effect on the stress intensity factor, while the plate thickness ratio has nothing to do with the stress intensity factor. The comparisons between FE solutions and analytical solutions show a good agreement. Chung et al. [8] analyzed the effects of lack-of-penetration crack size, weld leg size, and main plate thickness on mixed-mode stress intensity factors of load-carrying fillet welded cruciform joints using the finite element method and the least-squares method, and the general formulae of modes I and II stress intensity factors obtained from numerical results were verified by experimental results. Pasca et al. [9] determined the 3D stress intensity factors along the crack growth path of quarter-elliptical corner cracks for T joint using FRANC3D in tension and bending loadings; crack growth paths were obtained from Paris’ law based on the maximum tensile stress criterion. Pang et al. [10] studied the 3D stress intensity factor and weld toe magnification factor of a semielliptical weld toe crack for T-butt joint using the three-dimensional extended finite element method. They investigated the modeling of fatigue crack growth of weld toe semielliptical surface cracks for initial surface cracks with crack depth to plate thickness ratio (a/T) of 0.01 and three different crack aspect ratios (a/c) of 0.25, 0.5, and 1.0. The above studies did not consider the effect of corrosion damages on the stress intensity factor. Ghidini et al. [11] simulated corrosion-damaged areas of the specimen surface using a single semielliptical surface crack and a single through edge crack. Cerit [12] modeled the corrosion pit as a semielliptical notch based on the finite element analyses. Generally, corrosion pits can be modeled as cracks or notches in numerical simulation. In all the aforementioned research, however, the effects of corrosion and complex stress fields on the stress intensity factor were studied separately. To date, the stress intensity factor of welded steel joints has never been studied with the simultaneous presence of prior corrosion and complex stress fields.

This paper studies the stress intensity factor of full penetration, load-carrying, fillet cruciform welded joints with 45° inclined angle under prior corrosion and complex stress fields. A numerical model of welded joints is established using FRANC3D, considering the effects of pit depths, crack aspect ratios, and crack depths. Some useful conclusions are obtained for the numerical simulation of crack growth of welded joints under prior corrosion and complex stress fields.

2 Computation of the stress intensity factor

It is assumed that u, v, and w are the displacement components along the x-, y-, and z- directions, respectively. The element near crack tip using a polar coordinate system is shown in Fig. 1.

Fig. 1
figure 1

Model of a 3D crack

Full size image

According to the linear elastic fracture mechanics, the stress and displacement fields near the crack tip can be expressed as follows.

Mode I:

$$\sigma_{x} = \frac{{K_{\text{I}} }}{{\sqrt {2{{\pi }}r} }}\cos \frac{\theta }{2}\left[ {1 - \sin \frac{\theta }{2}\sin \frac{3\theta }{2}} \right],$$
(1)
$$\sigma_{y} = \frac{{K_{\text{I}} }}{{\sqrt {2{{\pi }}r} }}\cos \frac{\theta }{2}\left[ {1 + \sin \frac{\theta }{2}\sin \frac{3\theta }{2}} \right],$$
(2)
$$\tau_{xy} = \frac{{K_{\text{I}} }}{{\sqrt {2{{\pi }}r} }}\sin \frac{\theta }{2}\cos \frac{\theta }{2}\cos \frac{3\theta }{2},$$
(3)
$$\tau_{xz} = \tau_{yz} = 0,$$
(4)
$$\left\{ \begin{aligned} \sigma_{z} = \nu \left( {\sigma_{x} + \sigma_{y} } \right)\;\;\;\;\;{\text{for}}\;{\text{plane}}\;{\text{strain,}} \hfill \\ \sigma_{z} = 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\text{for}}\;{\text{plane}}\;{\text{stress,}} \hfill \\ \end{aligned} \right.$$
(5)
$$u = \frac{{K_{\text{I}} }}{4\mu }\sqrt {\frac{r}{{2{{\pi }}}}} \left[ {\left( {2\kappa - 1} \right)\cos \frac{\theta }{2} - \cos \frac{3\theta }{2}} \right],$$
(6)
$$v = \frac{{K_{\text{I}} }}{4\mu }\sqrt {\frac{r}{{2{{\pi }}}}} \left[ {\left( {2\kappa + 1} \right)\sin \frac{\theta }{2} - \sin \frac{3\theta }{2}} \right],$$
(7)
$$\left\{ \begin{array}{ll} w = 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\text{for}}\;{\text{plane}}\;{\text{strain,}} \hfill \\ w = - \int {\frac{\nu }{E}\left( {\sigma_{x} + \sigma_{y} } \right){\text{d}}z\;\;\;\;\;\;\;{\text{for}}\;{\text{plane}}\;{\text{stress;}}} \hfill \\ \end{array} \right.$$
(8)

Mode II:

$$\sigma_{x} = { - }\frac{{K_{\text{II}} }}{{\sqrt {2{{\pi }}r} }}\sin \frac{\theta }{2}\left( {2 + \cos \frac{\theta }{2}\cos \frac{3\theta }{2}} \right),$$
(9)
$$\sigma_{y} = \frac{{K_{\text{II}} }}{{\sqrt {2{{\pi }}r} }}\sin \frac{\theta }{2}\cos \frac{\theta }{2}\cos \frac{3\theta }{2},$$
(10)
$$\tau_{xz} = \tau_{yz} = 0,$$
(11)
$$u = \frac{{K_{\text{II}} }}{4\mu }\sqrt {\frac{r}{{2{{\pi }}}}} \left[ {\left( {2\kappa + 3} \right)\sin \frac{\theta }{2} + \sin \frac{3\theta }{2}} \right],$$
(12)
$$v = - \frac{{K_{\text{II}} }}{4\mu }\sqrt {\frac{r}{{2{{\pi }}}}} \left[ {\left( {2\kappa - 2} \right)\cos \frac{\theta }{2} + \cos \frac{3\theta }{2}} \right],$$
(13)
$$\left\{ \begin{array}{ll} w = 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\text{for}}\;{\text{plane}}\;{\text{strain,}} \hfill \\ w = - \int {\frac{\nu }{E}\left( {\sigma_{x} + \sigma_{y} } \right){\text{d}}z\;\;\;\;\;\;\;{\text{for}}\;{\text{plane}}\;{\text{stress;}}} \hfill \\ \end{array} \right.$$
(14)

Mode III:

$$\tau_{xz} = - \frac{{K_{\text{III}} }}{{\sqrt {2{{\pi }}r} }}\sin \frac{\theta }{2},$$
(15)
$$\tau_{yz} = \frac{{K_{\text{III}} }}{{\sqrt {2{{\pi }}r} }}\cos \frac{\theta }{2},$$
(16)
$$\sigma_{x} = \sigma_{y} = \sigma_{z} = \tau_{xy} = 0,$$
(17)
$$w = \frac{{K_{\text{III}} }}{\mu }\sqrt {\frac{2r}{{{\pi }}}} \sin \frac{\theta }{2},$$
(18)
$$v = u = 0,$$
(19)

where \(r\) and \(\theta\) are polar coordinates at the crack tip; \(\sigma_{x}\), \(\sigma_{y}\), \(\sigma_{z}\), \(\tau_{xy}\), \(\tau_{xz}\), and \(\tau_{yz}\) are stress components; \(\mu\) is shear modulus; E is Young’s modulus; \(\nu\) is Poisson’s ratio; \(K_{\text{I}}\), \(K_{\text{II}}\), and \(K_{\text{III}}\) are stress intensity factors of modes I, II, and III, respectively; and \(\kappa\) is expressed as

$$\left\{ \begin{array}{ll} \kappa = 3 - 4\nu \qquad \qquad \; {\text{for}}\;{\text{plane}}\;{\text{strain,}} \hfill \\ \kappa = {{\left( {3 - \nu } \right)} \mathord{\left/ {\vphantom {{\left( {3 - \nu } \right)} {\left( {1 + \nu } \right)}}} \right. \kern-0pt} {\left( {1 + \nu } \right)}} \quad {\text{for}}\;{\text{plane}}\;{\text{stress}} .\; \hfill \\ \end{array} \right.$$
(20)

Stress intensity factors of modes I, II, and III can be defined by the corresponding stress and displacement fields as

$$K_{\text{I}} = \mathop {\lim }\limits_{r \to 0} \sqrt {2{{\pi }}r} \sigma_{y} \left( {r,0} \right),$$
(21)
$$K_{\text{II}} = \mathop {\lim }\limits_{r \to 0} \sqrt {2{{\pi }}r} \tau_{xy} \left( {r,0} \right),$$
(22)
$$K_{\text{III}} = \mathop {\lim }\limits_{r \to 0} \sqrt {2{{\pi }}r} \tau_{yz} \left( {r,0} \right).$$
(23)

3 Numerical simulation of stress intensity factors of welded joints under prior corrosion and complex stress fields

FRANC3D can be conveniently used for crack simulation, and it uses the boundary element method and linear elastic fracture mechanics to analyze cracked structures [13, 14]. With FRANC3D, the geometry of three-dimensional structures with nonplanar cracks, multiple cracks, and user-defined cracks with arbitrary shape can be simulated [15]. The simulation process is as follows. Firstly, an uncracked finite element model is usually created using commercial finite element software, such as ABAQUS, ANSYS, and NASTRAN. Secondly, the model is imported into FRANC3D, and then a crack is inserted into the model according to its location. The user can remesh the model using 3- or 6-node triangular elements, or 4- or 8-node quadrilateral elements. Finally, the stress and displacement analysis is carried out with commercial finite element software. According to the results, stress intensity factors for all points along the crack front are computed using FRANC3D based on the interaction integral method or the displacement correlation method. In this paper, the stress intensity factor is calculated by FRANC3D with ABAQUS.

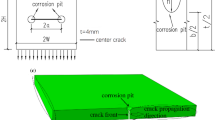
To simulate the complex stress fields, full penetration, load-carrying, fillet cruciform welded joints with 45° inclined angle were prepared with Q345qC steel according to [16], as shown in Fig. 2. A power exponential relationship between pit depth and time in atmospheric corrosion environment [17, 18] can be expressed as

$$d = 0.062t^{0.862} ,$$
(24)

where d is pit depth (mm); t is time (year). Different artificial spherical pits were fabricated on the surface of joints to conveniently simulate the prior corrosion. Dimensions of cruciform welded joints with pits are shown in Fig. 3, and sizes of the pits are shown in Table 1.

Fig. 2
figure 2

The specimen structure of the cruciform welded joint (unit: mm)

Full size image
Fig. 3
figure 3

Dimensions of cruciform welded joints with pits (unit: mm)

Full size image
Table 1 Sizes of pits (mm)
Full size table

In general, fatigue cracks are more likely to occur at the position of weld toe or root of welded steel structures. According to literature [16], most of cracks form at the end of weld toe of short side close to the direction of loading. It is assumed that an initial crack is a quarter-circular corner crack. The crack depth a and half-length c are assumed to be 0.25 mm [19, 20]. A uniform axial tensile stress of 160 MPa is applied at one end of the plate, and the fixed constraint is applied at the other end of the plate. The numerical model of a welded joint with corrosion pits is shown in Fig. 4.

Fig. 4
figure 4

Numerical model of a welded joint with corrosion pits

Full size image

4 Sensitivity analysis of stress intensity factors for welded joints under prior corrosion and complex stress fields

It is sufficient to describe the surface crack as a quarter ellipse with depth a and half-length c and to know the stress intensity factor at the surface point and at the deepest point only. The surface point and the deepest point of the crack are shown in Fig. 4. According to literature [21] and [22], pit size, crack aspect ratio (a/c), and crack depth (a) are the main factors influencing the stress intensity factor under prior corrosion and complex stress field. The sensitivity of stress intensity factors to these aspects is analyzed in this section. The parameters of pit radii (R = 1.0 and 2.0 mm), pit depths (d = 0.0, 0.5, 1.0, and 2.0 mm), crack aspect ratios (a/c = 0.4, 0.6, 0.8, and 1.0), and crack depths (a = 0.25, 0.30, 0.35, 0.4, 0.45, and 0.50 mm) are considered.

4.1 Effect of pit size

It is assumed that a = 0.25 mm; a/c = 0.4, 0.6, 0.8, and 1.0; R = 1.0 and 2.0 mm; d = 0.0, 0.5, 1.0, and 2.0 mm. Firstly, stress intensity factors under different pit radii are calculated and shown in Table 2. It can be seen from the table that the maximum of \(K_{\text{II}}\) and \(K_{\text{III}}\) at the surface point is about −5.8 % of \(K_{\text{I}}\), and the maximum of \(K_{\text{III}}\) at the deepest point is about −8.9 % of \(K_{\text{I}}\). Therefore, the effects of \(K_{\text{II}}\) and \(K_{\text{III}}\) at the surface point and \(K_{\text{III}}\) at the deepest point are neglectable. With an increase in the crack aspect ratio, \(K_{\text{I}}\) decreases at the deepest point, but decreases at the surface point. With an increase in the pit radius, \(K_{\text{I}}\) increases at the deepest point, but decreases at the surface point. Generally, the effect of pit radius on the stress intensity factor is relatively small.

Table 2 Stress intensity factors under different pit radii (MPa·mm1/2)
Full size table

In order to study the effect of pit depth on stress intensity factor, different pit depths are considered at the same pit spherical radius R = 2.0 mm. The effects of pit depth on stress intensity factors under different crack aspect ratios are shown in Figs. 5, 6, and 7.

Fig. 5
figure 5

The relationship between \(K_{\text{I}}\) at the deepest point and pit depth d under different crack aspect ratios

Full size image
Fig. 6
figure 6

The relationship between \(K_{\text{II}}\) at the deepest point and pit depth d under different crack aspect ratios

Full size image
Fig. 7
figure 7

The relationship between \(K_{\text{I}}\) at the surface point and pit depth d under different crack aspect ratios

Full size image

It can be seen from Fig. 5 that \(K_{\text{I}}\) at the deepest point decreases slightly at first and then increases with an increase in pit depth. \(K_{\text{I}}\) at the deepest point reaches its minimum and maximum at d = 0.5 and 2.0 mm, respectively. When the pit depth varies from 0.5 to 1.0 mm, \(K_{\text{I}}\) at the deepest point increases by 7.3 %, 4.3 %, 3.7 %, and 3.3 % at a/c = 0.4, 0.6, 0.8, and 1.0, respectively. In contrast, \(K_{\text{II}}\) at the deepest point decreases with an increase in pit depth (Fig. 6). When the pit depth varies from 0.0 to 2.0 mm, \(K_{\text{II}}\) at the deepest point decrease by 27.4 %, 22.0 %, 18.6 %, and 16.3 % at a/c = 0.4, 0.6, 0.8, and 1.0, respectively. As observed from Fig. 7, \(K_{\text{I}}\) at the surface point also increases with an increase in pit depth. When the pit depth varies from 0.0 to 2.0 mm, \(K_{\text{I}}\) at the surface point increases by 28.6 %, 18.5 %, 13.9 %, and 11.5 % at a/c = 0.4, 0.6, 0.8, and 1.0, respectively.

4.2 Effect of crack aspect ratio

Assuming a = 0.25 mm, and a/c = 0.4, 0.6, 0.8, and 1.0, the effects of crack aspect ratio on stress intensity factors under different pit depths are shown in Figs. 8, 9 and 10.

Fig. 8
figure 8

The relationship between \(K_{\text{I}}\) at the deepest point and crack aspect ratio a/c under different pit depths

Full size image
Fig. 9
figure 9

The relationship between \(K_{\text{II}}\) at the deepest point and crack aspect ratio a/c under different pit depths

Full size image
Fig. 10
figure 10

The relationship between \(K_{\text{I}}\) at the surface point and crack aspect ratio a/c under different pit depths

Full size image

As can be seen, \(K_{\text{I}}\) at the deepest point decreases with an increase in the crack aspect ratio (Fig. 8). When the crack aspect ratio varies from 0.4 to 1.0, \(K_{\text{I}}\) at the deepest point decreases by 19.0 %, 19.2 %, 19.5 %, and 22.2 % at d = 0, 0.5, 1.0, and 2.0 mm, respectively. By comparison, \(K_{\text{II}}\) at the deepest point decreases with an increase in the crack aspect ratio when \(d \, \le\) 0.5 mm (Fig. 9). When \(d \, \ge\) 1.0 mm, with the crack aspect ratio increasing, \(K_{\text{II}}\) at the deepest point increases at first and then decreases. \(K_{\text{I}}\) at the surface point increases with an increase in the crack aspect ratio. When the crack aspect ratio varies from 0.4 to 1.0, \(K_{\text{I}}\) at the surface point increases by 40.8 %, 35.2 %, 30.3 %, and 22.0 % at d = 0, 0.5, 1.0, and 2.0 mm, respectively.

4.3 Effect of crack depth

Assuming a = 0.25, 0.30, 0.35, 0.40, 0.45, and 0.50 mm, and a/c = 1.0, the effect of crack depth on stress intensity factors under different pit depths are shown in Figs. 11, 12, and 13.

Fig. 11
figure 11

The relationship between \(K_{\text{I}}\) at the deepest point and crack depth a under different pit depths

Full size image
Fig. 12
figure 12

The relationship between \(K_{\text{II}}\) at the deepest point and crack depth a under different pit depths

Full size image
Fig. 13
figure 13

The relationship between \(K_{\text{I}}\) at the surface point and crack depth a under different pit depths

Full size image

We can see that \(K_{\text{I}}\) at the deepest point increases with an increase in the crack depth (Fig. 11). When the crack depth varies from 0.25 to 0.50 mm, \(K_{\text{I}}\) at the deepest point increase by 14.8 %, 15.2 %, 15.7 %, and 16.5 % at d = 0, 0.5, 1.0, and 2.0 mm, respectively. Also, \(K_{\text{II}}\) at the deepest point increases with an increase in the crack depth except d = 2.0 mm (Fig. 12). When the crack depth varies from 0.25 to 0.50 mm, \(K_{\text{II}}\) at the deepest point increases by 5.7 %, 4.7 %, and 1.7 % at d = 0, 0.50, and 1.0 mm, respectively, but decreases by 8.1 % at d = 2.0 mm. At the surface point (Fig. 13), \(K_{\text{I}}\) increases similarly with an increase in the crack depth. When the crack depth varies from 0.25 to 0.50 mm, \(K_{\text{I}}\) at the surface point increases by 15.2 %, 17.5 %, 20.1 %, and 22.2 % at d = 0, 0.5, 1.0, and 2.0 mm, respectively.

5 Conclusions

Based on the computation theory of stress intensity factor, the stress intensity factor of welded joints with 45° inclined angle under prior corrosion and complex stress fields is simulated using FRANC3D. The sensitivity of stress intensity factors to pit size, crack aspect ratio, and crack depth is analyzed through a numerical simulation based on the above computation theory. From the numerical results for the cruciform weld joints with 45° inclined angle, some conclusions can be drawn as follows:

  1. 1.

    Pit depth plays an important role in stress intensity factor, while the effect of pit radius is relatively small. The cracking modes of the surface and the deepest point are mode I, and mixed modes I and II, respectively.

  2. 2.

    The effect of pit depth on \(K_{\text{I}}\) at the deepest point is not significant. A decrease in the crack aspect ratio induces a larger effect of pit depth on \(K_{\text{II}}\) at the deepest point and \(K_{\text{I}}\) at the surface point. The effect of crack aspect ratio and crack depth on \(K_{\text{II}}\) at the deepest point is both relatively small, but a decreased pit depth induces a larger effect of crack aspect ratio on \(K_{\text{I}}\) at the surface point.

  3. 3.

    In general, effects of pit depths, crack aspect ratios, and crack depths on stress intensity factor at the surface point is greater than at the deepest point.