Abstract
Stiffness is one of the basic performance parameters for railway track. The efficient and accurate stiffness measurement has been considered as the foundation for further development of railway engineering, and therefore has great theoretical and practical significance. Based on a summary of the connotation and measurement of track stiffness, the state of the art of measurement methods for track stiffness was analyzed systematically. The standstill measurement of track stiffness can be performed with the traditional jack-loading method, impact hammer method, FWD (falling weight deflectometer) method, and track loading vehicle method. Although these methods can be adopted in stiffness measurement for a section of railway track, they are not desirable owning to small range and low efficiency. In the recent 20 years, researchers have proposed many methods like unbalanced-loading laser displacement method, deflection basin deformation rate method, and eccentricity excitation method to continuously measure track stiffness; however, these methods have drawbacks like poor accuracy, low speed, and insufficient data analysis. In this work, the merits and demerits of these methods were summarized, and optimization suggestions were presented. Based on the wave transmission mechanism and principle of vibration energy harvesting, an overall conception on continuous measurement of stiffness and long-term stiffness monitoring for special sections was proposed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Track structure, a load bearing and transmitting structure of railway system, has stiffness to provide necessary elasticity. Track structure comprises several layers and each layer has its own stiffness, namely the track component stiffness. The overall track stiffness is usually adopted to characterize the total stiffness of all layers and reflect the stiffness characteristics of the whole track structure [1, 2]. The stiffness measurement of a track, generally, refers to measuring the overall stiffness. In laboratory tests, the stiffness of certain track component can be measured, such as fastener stiffness and ballast stiffness [3, 4].
Discrete rail support model and continuous rail support model are two classical models for the traditional mechanical analysis of railway track [1, 2]. In the discrete rail support model, the stiffness of fastener supporting track is a spring constant, while in the continuous rail support model, it is denoted by track modulus, which is calculated with the spring constant divided by the spacing between centers of discrete supports. The stiffness measurement method based on the Winkler elastic foundation model uses track modulus to characterize the overall track stiffness.
The track stiffness can also be classified into dynamic stiffness and static stiffness [2, 5, 6]. The resistance of track structure to deformation under a static load is called as static stiffness, which, usually, is determined by the deformation degree of track structure under the static load. The dynamic stiffness refers to the resistance of track structure to deformation under certain dynamic excitation, which is determined by the natural frequencies of track structure. The track dynamic stiffness reflects the supporting performance of the vibrating track structure and therefore is an important factor influencing the wheel–rail interaction and train running performance. However, the static stiffness is always adopted instead for the traditional mechanical analysis of the wheel–rail system. The rapid development of high-speed railway passenger transportation, heavy-loaded train transportation, and railway engineering technologies makes the theoretical analysis and practical measurement of dynamic stiffness significant.
Suppose that under load P the rail beam will deform. If the deformation amount is y, the track static stiffness K will be
Track structure is characterized by material nonlinearity and geometrical nonlinearity [7]. For example, the rubber pad in the fastening system is of material nonlinearity, and voids are distributed between the sleeper and ballast. Thus, the track static stiffness is also nonlinear, as shown in Fig. 1.
In order to take into account the nonlinearities of track structure, the track static stiffness is usually calculated by the slope of the linear part of the loading history curve [2, 8]. In this sense, the tangent stiffness and secant stiffness on the loading curve or unloading curve can be defined:
where a and b can be defined according to the specific requirement. For example, define b as the final loading state and a as the exact release state of the fastener clamping force.
The dynamic stiffness is influenced by many factors, such as the applied load and the frequency of excitation [9–11]. In order to conduct a quantitative study on the influence of the factors like loading frequency and amplitude on the track dynamic stiffness, a vertical harmonic force P = P 0ejωt is exerted on the rail. If the dynamic displacement at the force acting point is Z = Z 0ej(ωt+φ), the track dynamic stiffness can be defined as the ratio of the acting force amplitude to the dynamic displacement amplitude:
Under this definition, the track dynamic stiffness can be adopted to reflect the stiffness characteristics in steady forced vibration at a certain frequency.
In mechanical engineering, the dynamic stiffness is always studied in frequency domain. Similarly, the dynamic force and dynamic displacement can be processed through Fourier transform or to use the transfer functions by assuming that the stiffness is linear to some extent. Thus, the track dynamic stiffness can be defined as the ratio of dynamic load to dynamic displacement in frequency domain:
Now, the track dynamic stiffness is a complex value, with the amplitude and phase [8, 12]. The track dynamic stiffness can also be measured and analyzed through its reciprocal, namely the track dynamic flexibility.
2 Significance of track stiffness measurement
Track stiffness is an important factor influencing the safety and stability of train operation and the vibration and deformation of track structure as well as the dynamic response of substructures like subgrades and bridges [13–22].
Researches in relation to track stiffness mainly focus on three aspects: ① the analysis of the influence of track stiffness on the vehicle-track-substructure coupled dynamics; ② the nonlinear characteristics of track component stiffness, such as the nonlinearities of the rubber pad; and ③ the evaluation methods of track stiffness and the reasonable stiffness for track structure and its components.
2.1 Stiffness design of new railway lines
Stiffness design of new railway lines is to determine overall track stiffness and track component stiffness to meet the operation conditions of new railways. The measurement of track stiffness can help evaluate the stiffness design of new railways and present the relevant modification opinions.
2.2 Daily maintenance of railway lines
Track stiffness is also an important parameter for maintenance of railway lines in addition to the track geometric irregularity [23]. For most maintenance methods, the track geometric irregularity of railway lines is always adopted as the diagnostic parameter. The track geometry can be adjusted by ballast tamping to keep it within the limited range. However, the performance of ballasts, mostly, is dependent on the performance of bottom subgrade or other substructures. Ballast tamping cannot help improve the performance of substructures, such that track geometric irregularity repeatedly occurs.
The measurement of track stiffness for maintenance purpose covers four aspects:
-
(1)
Low track stiffness The railways built in soft soil areas and bad soil zones tend to experience serious rail displacement and fast cracking of track components after a period of operation. These diseases are mainly caused by poor stiffness of soil subgrade and therefore it should be strengthened. It is very important for checking the railway lines in time to keep safe train operation.
-
(2)
Variable track stiffness The stiffness always changes abruptly at the railway–bridge, railway–tunnel, and bridge–tunnel sections, and therefore transition zones shall be set [24]. Besides, when track geometric irregularity is deteriorated, support for the track will be uneven.
-
(3)
Virtual track stiffness Diseases, such as dirty ballast, hanging sleepers, and loose fasteners, can cause deformation and holes, leading to virtual stiffness for the rail support. The virtual stiffness represents potential risk to safe train operation.
-
(4)
Assortative stiffness The unmatched supporting stiffness of the right and left rails will result in uneven rail displacement, which can cause center bending of sleepers as well as the other unreasonable stress and cracking problems of track components.
The measurement of track stiffness can help direct the routine maintenance of railway lines and provide a reliable basis for making optimal maintenance strategies.
3 Track stiffness measurement methods
3.1 Standstill measurement
The standstill measurement of overall track stiffness means that a measurement point is decided in advance, and then the overall track stiffness can be calculated by measuring displacement and vertical force exerted on this point.
The overall track stiffness, generally, can be measured based on four methods: (1) traditional hydraulic jack-loading method [1, 2], (2) impact hammer method [25, 26], (3) FWD method [9, 27], and (4) TLV method [2, 5, 28–31].
In the traditional hydraulic jack-loading method, a certain force is exerted on the rail and then rail deflection is measured with a displacement meter or a dial indicator, and thus the force–displacement curve can be obtained (see Fig. 2). The overall track stiffness can then be calculated according to stiffness definitions like secant stiffness or tangent stiffness.
The traditional hydraulic jack-loading method has been adopted since the beginning of the twentieth century. Figure 3 shows a flatbed trailer loaded with I-typed bars used by the Talbot Committee as a reaction wall to measure the track stiffness in 1918 [1].
In the impact hammer method, the track vibration is measured with acceleration transducers installed on rail or sleepers (track plates) after an impulse load is exerted on the track with an impact hammer. The hammer head is equipped with a force transducer to measure the impulse and thus the transfer function of the track can be obtained. At last, the track component stiffness and the overall track stiffness can be calculated through parameter identification (see Fig. 4). Typically, the impact hammer method can cover a frequency interval of 50–1,500 Hz, which depends on the material of the hammer head [32]. A soft-rubber hammer head is suitable for lower frequencies than a hard-metal one. The impact hammer method is not reliable for the frequencies less than 50 Hz.
In the FWD (falling weight deflectometer) method, a mass impacts a track and the vibration response is measured at the same time. Afterwards, the track stiffness characteristics can be explored through transfer function calculation or other methods. The FWD method, to a certain extent, can reflect the impact effect on a track when a train is running at a high speed. The standard FWD method uses a 125 kN free-falling mass to impact the track. The vibration response of track is generally measured with velocity transducers or geophones.
The principle for the track loading vehicle (TLV) method is the same as that of the traditional hydraulic jack-loading method. However, this method is easier and can provide a larger vertical force (see Fig. 5). Organizations that have TLVs include Transportation Technology Center, Inc. (TTCI) and DECAROTOR of the USA, the South Africa BSSM, Delft of Holland, the railway department of Sweden, etc.
Queensland University of Technology in Australia improved a movable track stiffness measurement vehicle based on common TLV. This vehicle is composed of three cars. The front one is a six-axle towing locomotive (weight of 90 tons) to tow the vehicle to the specified measurement point. The middle one is a buffer car for buffering the influence of the front car on the rear one during the measurement. The rear car is equipped with measurement instruments and is the key part of the vehicle. The rear car weighs 57 tons totally (each part of 14.3 tons) and is equipped with hydraulic jacks and displacement transducers to exert vertical force and measure track deflection basin. When the vehicle reaches the specified measurement point, the hydraulic jacks extend from both sides of the rear car and act on the track separately. The deflection basin is recorded by 22 transducers to calculate the track modulus.
3.2 Continuous measurements
By the time of November 2015, there are 61 high-speed railway lines in China, and the total mileage has reached 12,000 km. The rapid development of high-speed railway lines has made the accurate and continuous measurement of track stiffness extremely important.
The above methods for standstill measurement of overall track stiffness are arduous, time consuming, and not suitable for a long-distance and multi-point measurement. The maintenance of railway lines requires continuous track stiffness measurement equipment. Therefore, many organizations have started to develop vehicles for continuous track stiffness measurement.
As early as in 1997, China Academy of Railway Sciences (CARS) put forward the conception of a vehicle for track elasticity measurement [33]. This vehicle comprises a heavy car in the front and a light car in the rear. The axle load of the heavy car can be varied by adjusting the number of concrete blocks in the range of 150–250 kN. Thus, the influence of different train axle loads on the measured results can be obtained. The light car weighs 40 kN and is used to eliminate the clearances between the rail and sleeper as well as between the sleeper and ballast bed. The measurement equipment on both heavy and light cars is the same except for the axle load.
This vehicle measures track geometric irregularities, which is similar to the chord measurement method. The main purpose of the vehicle is to measure the elastic deformation y K of tracks, as shown in Fig. 6.
Principle for track elasticity measurement of CARS-stiffness equipment. a Measurement with no wheel load on track. b Measurement with the wheel load of heavy car a on track. c Measurement with the wheel load of light car b on track. △ is reference line error. y 0 rail surface irregularities when there is no load on track, y 1 hidden gaps between rail, sleeper, and ballast, y 2 sum of triangle, y 0, and y H chord measured value under the wheel load of heavy car a, y L chord measured value under the wheel load of light car b, y KH track elastic settlement under wheel load of heavy car a, yKL track elastic settlement under wheel load of light car b
As shown in Fig. 6, the track stiffness can be expressed as
Transportation Technology Center, Inc. in Pueblo, Colorado (USA), also developed a stiffness measurement vehicle, with similar measurement principle to CARS [34, 35]. As shown in Fig. 7, this vehicle comprises a heavy car, a light car, and a towing locomotive. The loading range of the heavy car is 1–55 kips (4–267 kN). The stiffness is measured under 10 kips (44 kN) or 40 kips (178 kN). The load for the light car is less than 3 kips, and the track geometric irregularity is measured under 2 kips (8.9 kN). This vehicle operates twice, under the static loads of 178 and 44 kN, respectively, and in two cases the static track irregularity must be excluded. In the dynamic measurement, it finds out areas with high or low stiffness (especially low-stiffness areas to identify ballast or subgrade diseases) and then sprays yellow coatings for performing standstill stiffness measurement. Under the load of 178 kN, the displacement measurement involves the whole track and subgrade, while under the load of 44 kN, it includes the rail, sleeper, and ballast. The measurement speed can reach 16 km/h.
In addition, the measurement principle for the stiffness measurement vehicle developed by Swiss Federal Railways (SBB 2007) is also similar to the above-mentioned ones [8]. This vehicle comprises a light car and a heavy car (see Fig. 8). The weight of the light car can be neglected. The weight of the heavy car is 20 tons. The vehicle speed is 10–15 km/h. Heidenhain LS 220 transducers are used for low-pass (cut-off wavelength of 10–20 m). The accuracy of displacement measurement can reach 0.2 mm.
At the beginning of the twenty-first century, the University of Nebraska (USA) commenced the research on track modulus measurement system [8, 36, 37]. This measurement system can also be used to explore the track modulus through measuring the vertical rail displacement according to the laser measurement method. The measurement vehicle is equipped with two laser sources, the vertical rail displacement can be obtained through measuring the distance between two laser lines, and then the track modulus could be calculated. The measurement system is shown in Figs. 9 and 10.
The measurement principle is shown in Figs. 11 and 12, where d is measured according to the camera view analysis and L 1, L 2, θ 1, θ 2, and H are all known values. After y r is obtained, an equation is established based on the Winkler foundation model. Solving this equation, one can obtain the track modulus.
The ZOYON Technology Co., Ltd of Wuhan University (China), is now investigating a deformation rate-based track stiffness measurement method to be applied in the movable stiffness measurement vehicles [38]. This method was first introduced by scholars of Delft University of Technology in Holland; however, no prototype car has been made [2, 39–41].
According to this method, during load moving, the deflection basins at load-acting points are similar to each other. The ratio of the vertical track deflection rate at one point of a deflection basin to the load moving rate along the railway line is the slope of track deflection line at this point (see Fig. 13). Namely,
where w′(x) refers to the vertical track deflection rate obtained based on the Winkler foundation beam model.
To measure the track deflection rate, the high-speed deflectograph system adopts laser Doppler sensors attached to a moving railway vehicle traveling at speeds of up to 130 km/h. The sensor layout and laser projection positions are shown in Fig. 14.
The European Research for an Optimised BALlasted Track (EUROBALT II) project indicates that track stiffness is another import parameter for optimal long-term maintenance strategies in addition to track geometric irregularity (Meissonnier 2000).
This project promotes Banverket (a railway department of Sweden) to develop a trolley for continuous measurement of vertical track stiffness, the measurement principle of which is shown in Fig. 15 [8, 36, 42–49].
The static load, dynamic load, and maximum speed of this trolley are 60 kN, 20 kN, and 30 km/h, respectively. This trolley can only run on straight sections and not on narrow curves or switches. This trolley can be excited with different frequencies but only one frequency for each run. This trolley has been used for many on-site measurements, which shows good repeatability and reproducibility.
Royal Institute of Technology (KTH) in Sweden built a new vehicle, called rolling stiffness measurement vehicle (RSMV), a rebuilt two-axle freight wagon. The RSMV, much more advanced than the prototype trolley, has one battery plate, one hydraulic system, and two oscillating mass bodies (see Fig. 16). The parameters of RSMV are listed: weight of each body of 4,000 kg, measurable axle weight of 180 kN or higher, max. oscillating amplitude for dynamic load of 60 kN, and measurement frequency of 50 Hz. The measurement speed can reach up to 50 km/h. Figure 17 shows the measurement principle of the RSMV, and its two sides are symmetrical. The measurement principle is similar to that of the trolley.
In order to compare the measurement results of the RSMV with that of the prototype trolley, a comparison test was performed, showing that, for those railway sections with the overall track stiffness less than 150 kN/mm, the results were almost the same, while for those hard sections, the results are quite different.
Sponsored by the Innotrack project (D2.1.9 INNOTRACK 2009), Portancemetre for measuring the overall track stiffness [8, 50, 51] was developed by the Centre d’Experimentation et de Rechrche (CETE–NC, Grand Quevilly, France) and Engineering Department (SNCF, Paris, France). This measurement vehicle comprises two parts, one is the core measurement system of demonstrator and the other is the technical carriage system. The technical carriage system carries the energy supply equipment, hydraulic system, and electronic devices. The core measurement system is installed with Type 417 single-axle wheel pairs. The technical carriage system is installed with Y25C bogie wheel pairs. The main transducers of the Portancemetre include unsprung mass accelerometer, chassis accelerometer, phase sensor (synchronous signal), and incremental distance encoder. Figure 18 shows the on-site Portancemetre measurement in Rouen, France.
A camera with a linear CCD sensor is mounted under the technical carriage to record and monitor the measured track surface. All measurements are monitored by the portable computer placed in the locomotive.
Figure 19 shows the measurement principle for Portancemetre.
The force of the measurement system exerted on a rail can be calculated by
where M 1 refers to the total mass, M 0 the unsprung mass, Г b the vertical acceleration of the vibrating wheel, Г c the vertical acceleration of the suspended mass, m·e the eccentric moment of the unbalanced system, ω the angular velocity of rotation, and φ the angle of rotation.
The vertical displacement z can be obtained by calculating the double integration of the vertical acceleration of the unsprung mass:
The overall track stiffness, over an average time period, can be obtained according to wheel–rail force and vertical displacement.
Figure 20 shows the typical force–displacement hysteresis curve. The static load and dynamic load per rail are about 50 and 20 kN, respectively.
4 Analysis and discussion of measurement methods
The standstill measurement is suitable for monitoring track stiffness and long-term stiffness of special sections; however, the development of continuous track stiffness measurement vehicles is still the main way for realizing long-distance stiffness measurement of whole railway lines. Table 1 shows the performance parameter comparison of the above track stiffness measurement vehicles.
From Table 1, the existing continuous measurements of track stiffness have four problems.
4.1 Inconsistent measurement concepts
At present, the measurement methods target at different stiffness: static stiffness, dynamic stiffness, or the track component stiffness, which makes it rather difficult to compare the measurement results of these measurement methods.
For instance, the exciting frequency is unnecessary for static stiffness measurement, while for dynamic stiffness measurement, it is requisite. Likewise, when the deformation rate (TU Delft and ZONYON) is to be measured, the vehicle shall run as fast as possible; when the steady dynamic stiffness is to be measured (CETE-NC and SNCF), the vehicle speed cannot be too high. Hence, the measurement of track stiffness, firstly, requires a unanimous stiffness notion that can reflect the track stiffness characteristics completely.
Relatively speaking, the track stiffness notions of the RSMV (KTH, Sweden) and Portancemetre (CETE-NC and SNCF, France) are more advanced. The notions indicate that the track stiffness relates to the exciting frequency, which agrees with the conclusions of many literatures [52–54]. Other notions are based on the Winkler support model, which are not suitable for exploring deep information about track stiffness though they may solve some practical engineering problems.
4.2 Incapability for high-accuracy measurement
All the above-mentioned measurement methods are not suitable for high-accuracy measurement. The accuracy of the laboratory test results are acceptable; however, the accuracy of field test results is not satisfactory. The measurement accuracy mainly depends on the accuracy of force and displacement sensors or acceleration measurements. The force measurement includes strain measurement and pressure intensity measurement of hydraulic system. The strain measurement is more sensitive and accurate. Laser method is more suitable for displacement measurement, which provides high accuracy. Although acceleration transducers have high accuracy, in continuous track stiffness measurement, noise (especially low-frequency noise) can greatly affect the measurement. In addition, error cannot be eliminated when the displacement is calculated through the double integration. Hence, for the acceleration measurement method, appropriate data processing and signal analysis technologies are required to ensure high displacement accuracy. In fact, the continuous track stiffness measurement can be graded according to the desired accuracy (10, 1, 0.1 kN/mm and so on) to save cost and reasonably use the measurement sources.
4.3 Low measurement speed
Measurement speed is always very important for continuous track stiffness measurement. Theoretically, high measurement is likely to produce more accurate results. The track deformation rate measurement method (TU Delft and ZONYON) has the quickest measurement speed. However, it has two defects: the static stiffness notion takes no account of the influence of railway stiffness irregularity and geometric irregularity, and it is hard to deal with the dilemma between the measurement speed, transducer accuracy, and equipment operation reliability. These problems limit the application of this measurement method.
The measurement speeds of the methods designed by the University of Nebraska (USA) and CARS are moderate, which are limited by the accuracy of laser displacement transducers. The RSMV designed by the KTH (Sweden) has rather low measurement speed, which is limited by the reliability of the hydraulic system as well as the accuracy of transducers.
The measurement speed of Portancemetre (CETE-NC and SNCF, France) cannot be too high because the force–displacement hysteresis curve is to be measured.
4.4 Insufficient data analysis
From the perspective of the excitation-response measurement, the system transfer characteristics (the stiffness information) can be obtained regardless of the excitation type as long as there is sufficient response information. Hence, the track stiffness information, to a great extent, depends on the analysis technology of data.
KTH (Sweden) takes the leading position in the analysis technology of data, which has investigated the relation between track stiffness and time frequency/spatial frequency, the phase information of track stiffness, and amplitude information.
In fact, the laser measurement method (University of Nebraska, USA, and CARS, China) can also collect more data because the real-time track vibration can be reflected through the laser displacement data.
Up to now, no quantitative research on the relation between track stiffness and exciting frequency, exciting intensity as well as the running speed has emerged, which is the main reason for inadequate analysis of the measurement data of continuous track stiffness.
5 Conclusions and suggestions
This paper summarizes the significance of track stiffness measurement, takes a wide view of track stiffness measurement methods around the world, including the standstill measurement and the continuous track stiffness measurement, and performs a comparison analysis of all the measurement methods.
-
(1)
Track stiffness is an important factor influencing the safety and reliability of train operation, the vibration and deformation of track structures, and the dynamic response of substructures like subgrades and bridges. The track stiffness measurement is of great theoretical and practical significance to the design of new railway lines and especially the railway maintenance works. The measurement of track stiffness for maintenance relates to four stiffness problems: low stiffness, variable stiffness, virtual stiffness, and assortative stiffness problems.
-
(2)
The standstill measurement of overall track stiffness is time consuming and hard to realize a long-distance and multi-point measurement for whole railway lines. The existing methods for continuous track stiffness measurement have four problems: a. inconsistent measurement concepts. A unified stiffness notion has not been proposed to reflect the track stiffness characteristics completely; b. poor ability for high-accuracy measurement. The measurement accuracy for force, displacement, or acceleration is hard to ensure, especially for high-speed measurement; c. low measurement speed. It is difficult to solve the dilemma between the measurement speed, transducer accuracy, and equipment operation reliability; and d. insufficient data analysis. Much more stiffness information is expected to explore using the advanced analysis technology of the measurement data.
The following suggestions are proposed considering the imperfection of existing stiffness measurements:
-
(1)
A definite stiffness notion should be established to completely reflect the track stiffness characteristics.
-
(2)
A theoretical and systematic research should be performed on the quantitative relation between track stiffness and the factors like exciting frequency, running speed, and vehicle axle load, as well as the influences of track stiffness and track geometric irregularities on the vibration response of the vehicle-track-substructure coupled dynamics, respectively.
-
(3)
In view of the accuracy requirement for stiffness measurement, the track stiffness measurement can be categorized based on three grades, namely low accuracy (10 kN/mm, substructure disease identification, for heavy haul railways mainly), medium accuracy (1 kN/mm, potential safety hazard checking), and high accuracy (0.1 kN/mm, evaluation of track regularity, for high-speed railways mainly). For example, for continuous measurement vehicle with low measurement accuracy, single-axle vehicle can be used. The axle load should be more than 150 kN to ensure the vertical measurement for subgrade, and one span length (sleeper pitch) along the railway line can be the measurement unit. For the continuous measurement with medium measurement accuracy, it is advised to use double-axle vehicle with axle loads of 20 and 100 kN, the vertical measurement range is limited to the track structure, and the measurement unit ranges from 1 to 4 span lengths. For continuous measurement vehicle with high measurement accuracy, it is advised to use double-axle vehicle with axle loads of 10 and 50 kN, the vertical measurement range is limited to the rail and fasteners, and 4–10 span lengths can be adopted as the measurement unit.
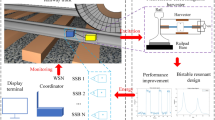
For transition zones (railway–bridge, railway–tunnel, and bridge–tunnel areas), turnouts, and small-radius curve sections, the track stiffness characteristics are more complicated than those of straight lines [2, 49]. Thus, apart from the measurements, the stiffness of special track sections can be monitored.
In recent years, the features of wave propagation in track structures have attracted a wide attention, and the wave theory is applied to the high-frequency vibration of rails [55]. Rail support conditions affect the transfer laws of track vibration waves, and thus continuous track stiffness measurement equipment can be developed based on the wave transfer mechanism.
In addition, the vibrations of track components and vehicle components can be collected for power generation [56–58]. Different track stiffness values cause different vibration intensities, affecting the collection of electric energy. When the stiffness measurement accuracy is undesirable because of poor noise reduction in vibration displacement and vibration acceleration signals, the vibration energy storage ability or real-time electrical signals (voltage, power, etc.) might be a good index for continuous track stiffness measurement or long-term stiffness monitoring of special sections.
References
Kerr AD (2000) On the determination of the rail support modulus k. Int J Solids Struct 37:4335–4351
Esveld C (2001) Modern railway track (second edition). MRT-Productions, Delft, pp 71–90
Zhang GM (2002) Research on right level of track structure stiffness and track-part stiffness. China Railw Sci 23(1):51–57
Liu L, Wang W, Liu W (2000) Experimental study of the static stiffness of ballast. J Shanghai Tiedao Univ 21(4):1–6
Liu W, Wang W (2002) Study on dynamic stiffness and damp measurement of railway crushed stone ballast. J China Railw Soc 24(6):99–104
Ooi LE, Ripin ZM (2011) Dynamic stiffness and loss factor measurement of engine rubber mount by impact test. Mater Des 32:1880–1887
Sussmann TR, Ebersöhn W, Selig ET (2001) Fundamental nonlinear track load-deflection behavior for condition evaluation. Transp Res Rec 1742:01–2916
Berggren E (2009) Railway track stiffness—Dynamic measurements and evaluation for efficient maintenance. Ph.D. Thesis, Royal Institute of Technology (KTH), Stockholm
Wu TX, Thompson DJ (1999) The effects of local preload on the foundation stiffness and vertical vibration of railway track. J Sound Vib 215(5):881–904
Chen XP, Wang P (2006) Distribution regularity and homogenization of track rigidity for ballastless turnout. J Southwest Jiaotong Univ 41(4):447–451
Chen XP (2008) Study on theory and application of track stiffness in high-speed turnouts. Ph.D. Thesis, Southwest Jiaotong University, Chengdu
Liu XY (2004) Effect analysis of track stiffness on dynamic characteristics of wheel–rail system and its dynamic optimization. J Southwest Jiaotong Univ 39(1):1–5
Lopez Pita A, Teixeira PF, Robusté F (2004) High speed and track deterioration: the role of vertical stiffness of the track. J Rail Rapid Transit 218:31–40
Cai CB, Xu P (2010) Dynamic analysis of key design parameters for ballastless track of high-speed railway. J Southwest Jiaotong Univ 45(4):493–497
Li D, Selig ET (1995) Evaluation of railway subgrade problems, Transportation Research Record 1489, TRB. National Research Council, Washington DC
Selig ET, Li D (1994) Creating track modulus: its meaning and factors influencing it. In: Transportation Research Record: Journal of the Transportation Research Board, No. 1470, Transportation Research Board of the National Academies, Washington, DC, pp 47–54
Frohling RD, Scheffel H, Ebersohn W (1996) The vertical dynamic response of a rail vehicle caused by track stiffness variations along the track. Veh Syst Dyn 25:17–31
Zhai JQ (2007) Test and analysis of vibration propagation caused by the subway train. Dissertation, Tongji University
Wu JZ (2012) The impact of vibration on the building structure caused by metro and isolation research. Dissertation, South China University of Technology
Wang P, Xu JH, Wang L (2014) Effect of track stiffness on frequency response of vehicle-track coupling system. J Railw Eng Soc 9:46–52
Robinet A, Hosseingholian M, Quibel A, Froumentin M (2008) Track stiffness assessment. In: 8th World Congress on Railway Research, Seoul, Korea, pp 1–8
Zhai WM, Cai CB, Kai KY (2000) Effect of track stiffness on train running behavior. J China Railw Soc 22(6):80–83
Ebersöhn W (1995) Substructure influence on track maintenance requirements. Ph.D. Dissertation, Department of Civil and Environmental Engineering, University of Massachusetts at Amherst
Konstantinos G, Spyridon T (2012) Transition zone between ballastless and ballasted track: influence of changing stiffness on acting forces. Proc Soc Behav Sci 48:3548–3557
Kaewunruen S, Remennikov A (2005) Application of experimental modal testing for estimating dynamic properties of structural components. In: Proceedings of Australian structural engineering conference 2005, Newcastle
Kaewunruen S, Remennikov A (2005) Monitoring structural degradation of rail bearing pads in laboratory using impact excitation technique. In: Proceedings of the 1st international conference on structural condition assessment, monitoring, and improvement, Perth, pp 389–394
Burrow MPN, Chan AHC, Shein A (2007) Falling weight deflectometer based inverse analysis of ballasted railway tracks. In: Geotechnical engineering, proceedings of the Institution of Civil Engineers, Issue GE3, pp 169–177
Kerr AD (1983) A method for determining the track modulus using a locomotive or car on multi-axle trucks. In: Proceedings AREA, vol 84
Kerr AD (1987) On the vertical modulus in the standard railway track analysis. Rail International, November Issue
Kerr AD On the reduced area method for calculating the vertical track modulus. In: Proceedings AREA, vol 86
Esveld C (1980) Track stiffness measurements using an adapted tamping machine. Rail International
D2.1.9 INNOTRACK (2009) Adapted “Portancemetre” for track structure stiffness measurement on existing tracks, Paris
Wangqing W, Geming Z, Kaiming Z, Lin L (1997) Development of inspection car for measuring railway track elasticity. In: Proceedings from 6th international heavy haul conference, Cape Town
Li D, Thompson R, Kalay S (2002) Development of continuous lateral and vertical track stiffness measurement techniques. In: Proceedings from railway engineering, London
Thompson R, Marquez D, Li D (2001) Track strength testing using TTCI’s track loading vehicle. Railw Track Struct 97:15–17
McVey B, Norman C, Wood N, Farritor S, Arnold R, Fateh M, El-Sibaie M (2005) Track modulus measurement from a moving railcar. In: Proceedings of the AREMA annual conference, Chicago, September 25–27, 2005
Norman C, Farritor S, Arnold R, Elias SEG, Fateh M, Sibaie ME (2004) Design of a system to measure track modulus from a moving railcar. In: Proceedings from railway engineering, London
Information from http://old.zoyon.com.cn
Rasmussen S, de Man AP (2000) The high speed deflectograph and the hammer excitation test: two measurement techniques for determining track performance. Rail Eng Int 2000(1):13–16
Rasmussen S, Man AP (1999) Measurement techniques for track performance. In: Proceedings of conference on innovations in the design and assessment of railway track, Technical University of Delft, Delft
Rasmussen S, Krarup JA, Hildebrand G, Non-contact deflection measurement at high speed. In: 6th International conference on the bearing capacity of roads, railways and airfields, 24–26 June, 2002, Lisbon
Berggren E, Jahlénius Å, Bengtsson B-E (2002) Continuous track stiffness measurement—an effective method to investigate the structural conditions of the track. In: Proceedings of the conference railway engineering—2002, London, 3–4 July, 2002. ISBN: 0-947644-49-0
Berggren E, Jahlénius Å, Bengtsson B-E, Berg M (2005) Simulation, development and field testing of a track stiffness measurement vehicle. In: Proceedings of 8th international heavy haul conference, Rio de Janeiro, 13–16 June, 2005. ISBN: 0-646-33463-8
Berggren E, Kaynia A, Dehlbom B (2010) Identification of substructure properties of railway tracks by dynamic stiffness measurements and simulations. J Sound Vib 329:3999–4016
Berggren E (2006) Measurements of track stiffness and track irregularities to detect short waved support conditions. In: Proceedings of international conference on railway track foundations, Birmingham, 11–13 September, 2006. ISBN: 0-704426-00-5
Berggren E, Li M, Spännar J (2006) A new approach to the analysis and presentation of vertical track geometry quality and rail roughness. In: Proceedings of 7th international conference on contact mechanics and wear of rail/wheel systems (CM2006), Brisbane, 24–27 September, 2006. Also in journal of WEAR, vol 265, pp 1488–1496
Berggren E (2009) Efficient track maintenance—methodology for combined analysis of condition data, submitted to the conference IHHA 2009. Candidate paper to Special Issue of J Rail Rapid Transit
Li M, Berggren E (2009) A study of the effect of global track stiffness and its variations on track performance: simulation and measurement, submitted to the conference IHHA 2009. Candidate paper to Special Issue of J Rail Rapid Transit
Smekal A, Berggren E, Silvast M (2006) Monitoring and substructure condition assessment of existing railway lines for upgrading to higher axle loads and speeds. In: Proceedings of 7th World Congress on Railway Research, Montreal, 5–7 June, 2006
Alexander R, Sakdirat K Laboratory measurements of dynamic properties of rail pads under incremental preload. In: 19th Australasian conference on the mechanics of structures and materials, Christchurch, pp 319–324
Hosseingholian M, Froumentin M, Robinet A (2006) Feasibility of a continuous method to measure track stiffness. In: Proceedings from railway foundations conference, Birmingham
Fenander A (1997) Frequency dependent stiffness and damping of railpads. Proc Inst Mech Eng Part F 211:51–62
Fenander A (1998) A fractional derivative railpad model included in a railway track model. J Sound Vib 212(5):889–903
Frohling RD (1998) Low frequency dynamic vehicle/track interaction: modeling and simulation. Veh Syst Dyn 28:30–46
Ryue J, Thompson DJ, White PR, Thompson DR (2008) Investigation of propagating wave types in railway tracks at high frequencies. J Sound Vib 315:157–175
Pourghodrat A, Nelson CA, Hansen SE, Kamarajugadda V, Platt SP (2014) Power harvesting systems design for railroad safety. Proc IMechE Part F 228:504–521
Wang JJ, Penamalli GP, Zuo L (2012) Electromagnetic energy harvesting from train induced railway track vibrations. In: Proceedings of IEEE/ASME international conference on mechatronics and embedded systems and applications (MESA), pp 29–34
Gao MY (2015) Design and verification of a rail-borne electromagnetic transducer for railway energy harvesting. Research report, Key Laboratory of High-speed Railway Engineering, Ministry of Education, Southwest Jiaotong University, Chengdu
Acknowledgments
This research was supported by the project (51425804) of the National Science Fund for Distinguished Young Scholars of China and the National Natural Science Foundation of China (NSFC) under grants U1234201, U1334203, and 51378439.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Wang, P., Wang, L., Chen, R. et al. Overview and outlook on railway track stiffness measurement. J. Mod. Transport. 24, 89–102 (2016). https://doi.org/10.1007/s40534-016-0104-8
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40534-016-0104-8