1 Introduction

Traffic flow models were developed to simulate and understand traffic operations. The models are mathematically theory-based or simulation-based [1]. Within these two categories, microscopic traffic flow models are extremely popular. It is believed that one of the earliest microscopic models is the car-following model proposed by Reuschel and Pipes [2]. This model regards vehicles as discrete particles and uses differential equation to capture the rule of motions of each vehicle under the situation that no overtaking behavior happens [4]. So the car-following model is basically a mathematical theory-based model. The original model was revised in the 90s by Bando [5] based on the dynamical non-linear effects proposed by Newell [6], after which a series of modifications were studied to optimize the model. More revised car-following models like generalized force model [7] were put forward and some revisions were made to take comfort factors during driving into account [8]. One revised psychological-and-physiological car-following model is now adopted by Vissim [9], a well-known microscopic traffic simulation software.

After the proposal of the car-following model, a cellular automation (CA) model was put forward by Cremer and Ludwig [10]. The model is discrete in both time and space, which is an effective simplification to approximate to the solution of differential equations. Compared with many car-following models, CA model can well simulate overtaking behaviors in highway with unidirectional two lanes [11]. In general, CA model belongs to simulation-based models for its clear evolution rules of vehicle operations. It is easy to implement on computer for its discreteness. With the rapid development of modern computers, this model becomes increasingly popular in the 90s [12]. Its popularity gains partly due to its flexible framework to incorporate traffic control and many other interesting components. For example, Horni et al. (2013) used CA model to conduct parking simulation, and they incorporated agent-based techniques as well [13]. Chai et al. (2015) made use of CA model to simulate traffic streams at signalized intersections. The thing incorporated is fuzzy logic, and results show the model can well replicate decision-making processes [14]. CA model can even be used to evaluate vehicle load effect in bridge construction [15].

Mathematically, theory-based models are appealing since they can promote the understanding of the mechanism how traffic streams evolve over time and space. However, these models sometimes are hardly accessible, which makes it difficult to put into practice. As for simulation-based ones, CA model is widely used for microscopic simulation of vehicles on freeway though defects exist as well. Efficient as CA model is, its feature of temporal and spatial discreteness is not in coincidence with real situations, which probably leads to inaccuracy in simulation results. In addition, it is the traffic flow characteristics like speed, density, and delay that most traffic flow models lay emphasis on, including the CA model. But these models are unable to evaluate vehicle safety condition that ought to be seriously considered. Actually, safety is the most important factor concerning traffic operations on freeway where high speed may cause serious accidents [16].

Based on the analysis above, a micro-simulation traffic flow model is put forward in this paper. The model is aimed at two-lane freeway that is quite common. It is the simplest form of freeway, which acts as the foundation of potential models targeted at the freeway with more than three unidirectional lanes. The proposed model is discrete in time, but continuous in space. This is more close to real situations than that of CA model. Besides, the model takes into consideration different types of drivers in terms of their overtaking behaviors. Compared with incorporating human factors into classic car-following models [17], it is much easier for the proposed model to achieve, which is understandable and has no trouble in solving more complicated equations. Finally, the safety coefficient in our model can conveniently make an evaluation of safety condition.

The remainder of this paper is organized as follows. In Sect. 2, all aspects of the proposed model are overviewed. Section 3 provides a preliminary test of the model, and Sect. 4 shows how the model evaluates safety condition on freeway. Some discussions are presented in Sect. 5 which is followed by a conclusion section.

2 Model overview

2.1 Basic assumptions

  1. (1)

    The freeway section is homogeneous.

  2. (2)

    Vehicles travel on the right lane unless they are steered to pass the front car. The left lane gets used when vehicles are overtaking others, in which case they move one lane to the left, pass, and return to their former travel lane. This is what is called the keep-right rule, which is quite common in the United States.

  3. (3)

    The arrival of vehicles conforms to Poisson distribution and we use the parameter of Poisson distribution to represent different traffic volume conditions.

  4. (4)

    All vehicles are able to be classified into three types: small car, medium car, and large car. Each kind of vehicle has its own speed limits and vehicle length.

  5. (5)

    Vehicles can be abstracted to a straight line from its tail end to head end. The crashes only happen at these two end points, or only rear-end crashes are considered.

  6. (6)

    Traffic safety on the two-way freeway is assumed to only have something to do with lane-changing behavior while the effects of speed are ignored.

2.2 Explanation of terminology

Key parameters to the model are summarized as follows:

V 0: the speed of the vehicle backward in the left lane.

V 1: the speed of the vehicle backward in the right lane.

V 2: the speed of the vehicle ahead in the left lane.

V 3: the speed of the vehicle ahead in the right lane.

D 1: the distance of the two adjacent vehicles ahead in the left lane.

d 2: the distance of the two adjacent vehicles ahead in the right lane.

δ: the discount factor of safety coefficient.

C(t): the safety coefficient at time t.

2.3 The micro-simulation model

Vehicle operation on two-lane freeway is determined by the driver behavior such as their driving skills, preferences, and so on. Besides, the type of vehicle, distance between two vehicles, speed limit, etc. also make a difference to traffic operations. Owing to these complicated factors, simplifications are needed to establish the micro-simulation model while it is indispensable to capture driver behaviors.

The simulation is set on a freeway section. Vehicles enter from one end of the section and exits from the other end. This model is discrete in time. In order to obtain accurate results from the simulation, the time interval cannot be too long. We set the time interval as 1 s. However, unlike cellular automata, our model is not spatially discrete. According to the basic assumptions, the arrival of vehicles conforms to Poisson distribution, so it is not difficult to figure out the probability of vehicle arrival in 1 s at the end where vehicles enter. We use a random number ranging from 0 to 1. When its value is bigger than this probability, there is a vehicle entering the section. The type of vehicle is determined by the percentage of various vehicle types. Thus, the actual situation of vehicle arrival is well simulated. The operations of vehicles will be updated every 1 s, including the instantaneous velocity of vehicles, the travel distance from the start, and the lane each vehicle occupies. Real-time traffic operations on the freeway section are reproduced in this way. Finally, a vehicle gets removed when its travel distance exceeds the length of the virtual section. The simulation ends when its operating time meets the requirement set by researchers.

The model has some application conditions. First, the freeway has just unidirectional two lanes. Second, the freeway section for simulation is supposed not to contain weaving areas or ramps. The proposed model can basically conduct simulation on any basic segment of two-way freeways. Anyway, basic segments constitute the most part of a freeway.

2.3.1 Explanation of parameters

  1. a.

    The affected distance

    The distance is defined according to which a driver decides whether to follow or overtake the front vehicle. The farthest distance that the driver can see under a certain speed is suggested to determine the affected distance in this paper.

  2. b.

    The safety distance

    The safety distance ensures there will approximately not be a crash even if drivers take extreme dangerous strategies to pass a car.

  3. c.

    The feasible-passing distance

    The feasible-passing distance determines whether or not a driver will brake when overtaking the front vehicle. If the actual distance between them is shorter than the feasible-passing distance, the driver should brake first and then speed up.

  4. d.

    The critical distance

    The critical distance is the minimum distance to pass a vehicle which ensures there will not be a crash if a driver takes safe strategies to make overtaking. It can be understood in another way that if the actual distance is shorter than the critical distance, no driver will choose to overtake.

  5. e.

    The extreme distance

    The extreme distance is the shortest distance that every two adjacent cars have to keep under any circumstance. The vehicle length is recommended to well characterize it.

Note that the distances defined above are all called “characteristic distance” in this study. They are some of the most important parameters to vehicle state update in the simulation.

  1. f.

    The safety coefficient

    We define the safety coefficient that ranges from 0 to 1. When the coefficient is close to 1, it means the vehicle operation is safe. The initial value of the coefficient is 1, and it will get lower and lower if vehicles meet safety problems. Mathematically, C(0) = 1, and the formula for updating the coefficient is

    $$C\left( {t + 1} \right) = C\left( t \right)\,{ \cdot }\,\delta .$$
    (1)
  2. g.

    The discount factor of safety coefficient

    δ is defined to reflect the degree of safety during lane-changing process based on assumption (5). Considering the safety is closely related to the distance between two adjacent vehicles while drivers change a lane [18], the method to figure out δ is determined as given below:

    1. (1)

      Lane changing aimed at overtaking, then

      $$\delta = k_{ 1}\, { \cdot }\,k_{ 2}\, { \cdot }\,k_{ 3} ,$$
      (2)

      k 1 = 0 when the distance between two adjacent cars lies between the critical distance and the feasible-passing distance. Although drivers are able to overtake, it is very dangerous under this circumstance.

      k 1 = 0.5 when the distance lies between the feasible-passing distance and safety distance. In this case, it is not safe enough to pass a car but there is little ground to blame drivers for this.

      k 1 = 1 when the distance is longer than the safety distance, which means it is absolutely safe for drivers to make overtaking.

      Similarly but slightly differently, k 2 has something to do with the front vehicle in the passing lane. Then the rule for determining k 2 is the same with that of k 1. In addition, the overtaking behavior will be affected by the vehicle behind in the passing lane. In this case, it should be more conservative of drivers who want to overtake to make judgments because errors are bigger when figuring out the condition of vehicle operation behind. Meanwhile, the speed of the vehicle behind in the passing lane is probably not as low as that of the car which is to be overtaken. In summary, the passing behavior had better been finished within the feasible-passing distance. When the distance between two adjacent vehicles is shorter than the feasible-passing distance, k 3 = 0; when the distance lies between the feasible-passing distance and safety distance, k 3 = 0.5; otherwise, k 3 = 1. Accordingly, δ can be calculated in the end.

    2. (2)

      Lane changing without overtaking

      It is much safer when a vehicle changes back from the left lane to the right lane, which is only affected by the car in the front because it is much faster than the car behind. Similarly, when the distance lies between the critical distance and safety distance, δ = 0.5, which means it is rather unsafe to change a lane; when the distance is longer than the safety distance, δ = 1.

  3. h.

    The average safety coefficient

    The safety coefficient is used to evaluate the safety condition of a single vehicle. To make safety evaluation aimed at the whole traffic flow entering the section in simulation, the average safety coefficient is defined to be the arithmetic mean of the safety coefficients of all vehicles.

2.3.2 The rule of lane changing

  1. a.

    Lane changing for overtaking

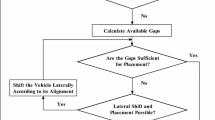
    The lane-changing conditions are more complex when the aim is to overtake than that of non-overtaking lane changing. First, a driver needs to judge the distance and speed concerning the vehicle in front of him. Only if the distance is shorter than the affected distance and the speed is not lower than that of the front car, the driver will choose to overtake or follow the car. Once the driver chooses to make overtaking, he has to determine whether the conditions of passing are satisfied. The passing behavior is permitted only if the distance between his and the vehicle in front of him in both right and left lane is longer than the critical distance, and the distance between his and the car backward in the passing lane is longer than the feasible-passing distance. He, otherwise, can only choose to follow the car ahead, which suits the case in real life well.

  2. b.

    Lane changing without overtaking

    The normal situation is that vehicles drive on the right lane under the keep-right rule. As a result, the conditions for lane changing back to the right lane is given below: There is no vehicle ahead in the right lane, or the distance away from the vehicle ahead exceeds the affected distance, or this distance is within the affected distance but beyond the extreme distance while the speed of the vehicle ahead is higher than the instantaneous speed when the overtaking is just finished. A detailed explanation of the lane-changing rules will be seen in the flow chart below. Note that in the simulation process, the speed when a vehicle changes to the passing lane is a mathematical expectation. The expected value of speed is random that lies between the minimum and maximum speed limits of the passing lane.

2.3.3 The rule of speed update

In the driving process, it is impossible for any driver to maintain a certain speed, especially when following a vehicle in the front. Speed fluctuation is also influenced by the driving behavior of the front car. In order to characterize this speed fluctuation in the simulation, we formulate the following four rules of speed update: the rule of traveling freely, the rule of car-following with reference, the rule of normal car-following, and the rule of close car-following.

  1. a.

    The rule of traveling freely

    The rule is that there is no vehicle beyond the affected distance in front of a driver. In this case, the speed fluctuation only relates to the driver himself. According to the psychological characteristics of drivers, the variation of speed can be determined as positive and negative 3 km/h.

  2. b.

    The rule of car-following with reference

    The rule is that the distance away from the front vehicle is between the critical distance and the affected distance, and the speed is lower than that of the vehicle ahead. In this case, fluctuation characteristics of speed have something to do with the driver and the front vehicle. Less distance away from the front vehicle causes less speed variation. In addition, the driver will slightly accelerate with a tendency to reach the same speed as that of the vehicle ahead according to “reference dependence,” a theory of behavior psychology. Consequently, the variation of speed is less than that of the rule of traveling freely, and the positive variation is dominant compared with negative variation.

  3. c.

    The rule of normal car-following

    The rule is that the distance away from the front vehicle is between the critical distance and the affected distance, and the speed is higher than that of the vehicle ahead. In this case, fluctuation characteristics of speed are related to the driver and the front vehicle as well. Therefore, the variation of speed is less than that of the rule of traveling freely, but unlike the rule of car-following with reference, the positive and negative variations are of the same.

  4. d.

    The rule of close car-following

    The rule is that the distance away from the front vehicle is shorter than the critical distance and the speed is not lower than that of the vehicle ahead. In this case, the driver and the front vehicle also both have effects on the speed fluctuation. Moreover, the driver becomes the most cautious for the distance between the two vehicles is sufficiently small. Therefore the variation of speed is less than that of the rule of normal car-following.

Considering the precision of speed fluctuation does not make a great effect on simulating vehicle operations, the variation of speed can be produced using random number generation method while it coincides with those rules of speed update above.

2.3.4 The rule of distance update

Because a vehicle’s trajectory is in two-dimensional plane, it is complex to determine the running distance of a vehicle directly. The traffic operations are approximate to be in one dimension. Therefore, the time interval is multiplied by the average speed at time t and t + 1 so as to obtain the running distance of a vehicle between the time t and t + 1.

The detailed framework of this simulation model is shown in the flow chart (Figs. 1 and 2). Through the simulation, traffic flow characteristics including speed, density, delay, and safety condition of different types of vehicles are obtained.

Fig. 1
figure 1

The rule of vehicle state update in the right lane

Full size image
Fig. 2
figure 2

The rule of vehicle state update in the left lane

Full size image

3 Partial test

The model is partially tested by comparing the simulation results with some qualitative analysis. On the basis of the analysis above, the extreme distance can be set as the maximum length of different types of small cars. Hence, the extreme distance is set to be 6 m in this test according to the official definition of small cars. Suppose that the critical distance, the feasible-passing distance, the safety distance, and the affected distance are 1.5, 2.0, 2.5, and 3.0 times as long as the extreme distance. The values of these distances are set solely to make a partial test to conduct a preliminary verification on the validity of our model. The annual average daily traffic volume of a two-way and four-lane freeway ranges from 25,000 to 55,000 veh/d [19], or 521 to 1,146 veh/h. Therefore, the traffic volume in this test is set to 1,050 veh/h, which is randomly picked out from the range [521, 1,146]. In this way, the saturation of traffic flow is not low without congestion occurring. We make the speed limit 80–100 km/h for small cars, and 60–80 km/h for medium and large cars for the right lane. With regard to the left lane, the speed limit is 100–120 km/h for small cars, and 80–100 km/h for medium and large cars. Meanwhile, the ratio of probability of the arrival for large cars, medium cars and small cars is 1:2:6.

After the simulation, the results of the delay are shown in Figs. 3, 4, and 5. From the three figures, it is found that the delay of small cars is the largest while that of large cars is the smallest. The reason is probably that the speed of small cars is affected by the medium and large cars ahead of them to a great extent. Chances are that it causes the difficulty in keeping normal speed for small cars based on the previous analysis that the saturation of traffic flow is not low. The number of points on these three graphs is different, which the ratio of arrival probability of all types of vehicles can account for. The number of points of small and large cars are the biggest and smallest, respectively.

Fig. 3
figure 3

The distribution of delay of small cars

Full size image
Fig. 4
figure 4

The distribution of delay of medium cars

Full size image
Fig. 5
figure 5

The distribution of delay of large cars

Full size image

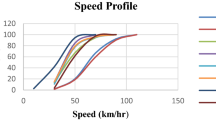
The results of the speed can be obtained at the same time. Some statistics are calculated and listed in Table 1. It is obvious the average speed of the three types of cars is all within the range of speed limit, and the mean of small cars is larger than that of medium cars as with the case of medium cars and large cars. Furthermore, the variance of the speed for small and medium cars is larger than that of the large cars, meaning that the speed of large cars has the least fluctuation. It is known drivers of large cars have little tendency to make overtaking in general. Therefore, these results all have coincidence with common sense.

Table 1 The mean and standard deviation of speed of different kinds of cars (unit: km/h)
Full size table

Last but not least, the validity of the proposed model can be tested using traffic fundamental diagram that captures the relationship between the density and flow (volume) of vehicles. Plenty of points can be determined by changing the traffic volume parameter in our model. Given the basic capacity of one vehicle lane that is about 2,000 veh/h according to the Ref. [20], the capacity of two-lane freeway is around 4,000 veh/h unidirectionally. Accordingly, the input of the mean demands (unit: veh/h) for each simulation are determined as is shown in the set S:

$$S \, = \, \left\{ {q|q \, = { 5}0x \, + { 2,}0 50, \, x \, \in \, \left\{ {0,{ 1},{ 2}, \, \ldots \, ,{ 36}} \right\}} \right\}.$$
(3)

In these 37 simulations, each time the traffic density can be figured out. Then the scatters are plotted in flow-density graph shown in Fig. 6. It can be concluded that these scatters generally accord with a triangular fundamental diagram. The critical density is about 44 veh/km and the maximum flow that just indicates the actual capacity of the freeway section is about 3,900 veh/h. Because 3,900 veh/h is smaller than 4,000 veh/h, this actual capacity seems fairly reasonable though hard to be proved. In general, the approximate reproduction of the fundamental diagram further verifies the validity of the proposed simulation model.

Fig. 6
figure 6

The scatters obtained by micro-simulation

Full size image

4 Safety evaluation

The safety coefficient defined in Sect. 2 is taken advantage of to make safety evaluation. The coefficient of each vehicle is recorded during the simulation, so the safety condition of different vehicles can be compared so that an evaluation is accessible. In addition, the average safety coefficient is able to reflect the safety of traffic flow. Some insights are expected to be made through having the traffic volume vary from light flow to heavy flow. The volume 1,050 veh/h discussed in Sect. 3 is continued to be used so as to represent a light flow whose V/C (the ratio of traffic volume to road capacity) is about 0.25 in this work. A medium flow and a heavy flow are also determined by random sampling like the way to determine 1,050 veh/h, and the results are shown in Table 2.

Table 2 The average safety coefficient under different flow levels
Full size table

According to the results, the average safety coefficient is the highest when the traffic flow is light, and the most dangerous situation takes place when a medium traffic volume is observed. This summary is likely to be reasonable because when there is a little traffic, the safety condition should be good for a great distance between every two adjacent cars. The safety is not bad under the situation of heavy flow because drivers start to become cautious to avoid crashes and their speed is passively reduced for a fairly high vehicle density. The most dangerous condition on the freeway is that there exists a medium traffic flow while vehicle speed keeps at a quite high level. As a consequence, assuming the proposed model has been proved to be valid in Sect. 3, the average safety coefficient that is put forward is effective in evaluating traffic safety condition.

5 Discussions

The key parameters to the proposed simulation model is the four characteristic distance: the affected distance, the safety distance, the feasible-passing distance, and the critical distance when the extreme distance is determined to be the vehicle length. Although it is not involved how to determine these distances in this paper, the implications of them are clear, resulting in potential mathematical models to figure out the formulas for solving them.

The keep-right-except-to-pass rule is the premise of our work, but the proposed model is also applicable in countries like Britain where vehicles run on the left. In this case, the only alternation is to interchange the right lane and left lane. Besides, the rule is common in countries like the United States but not dominant in many other countries. In any case, the framework of our model is flexible and some rules for the evolution of vehicle operations can be modified to approximate to other similar driving rules.

It is the continuity in space that makes our model significantly differ from CA model, which is more coincident with real situations. Besides, the driver behavior used in this model is also close to real life. To be specific, drivers first decide whether to overtake a car according to the distance and speed difference. Then they judge whether the conditions for overtaking are all satisfied. Finally they take actions staying in the origin lane or changing a lane. Hereby our model is a typical simulation about decision-making process in lane changing. In addition, the proposed model can make a market segmentation on drivers. Different types of drivers behave distinctively in overtaking, which is significant in obtaining reasonable results from the simulation. Finally, the safety condition can be simply obtained in our simulation. These are the key advantages of the proposed model.

Weaknesses, however, exist in our model at the same time. First, there are many assumptions for the model. Tenable as many of these assumptions may seem, a few of them such as assumption (5) is not really grounded because speed difference has something to do with safety. And it is hard to assess the impacts they have on the accuracy and precision of the proposed model while the validity of model is solely preliminarily tested in this study. Second, the rules of state update for driving is quite complex. Consequently, it is uneasy to achieve the simulation through programming, or extend the proposed model to freeway sections that have more than two lanes in one direction. Some simplifications could be made while valid model outputs are guaranteed.

6 Conclusions

In this paper, a micro-simulation model is put forward to make evaluation of traffic flow characteristics including safety condition. The model has some advantages over the classic CA model. A partial test has been conducted and the validity of our model is preliminarily verified. Future work can focus on the following aspects. First, some basic assumptions can be loosened. The probability distribution of the arrival of vehicles, for example, can be calibrated through real traffic flow data instead of Poisson distribution assumption. Second, methods to determine the model parameters can be focused on. Visibility is probably one of the most important factors that make a great difference to the proposed four characteristic distance. Third, the validity of our model requires further and more rigorous verifications. One possible method is to calculate the actual capacity of targeted freeway section on the basis of basic capacity, and comparison can be made between the calculation and the results obtained by our simulation. Another method is based on real flow data. Comparing, the data with the simulation results including speed, density, and delay, the validity of the model will be more strictly proved. Finally, multilane freeway traffic simulation can be achieved though the rules of vehicle state update in this study ought to be slightly revised. Taking three-lane freeway as an example, rules such that small cars never run in the right (nearside) lane while large cars never run in the left (fast) lane are necessary to make an extension of the proposed micro-simulation model.