Abstract
The road weather information system (RWIS), which collects and monitors weather and pavement surface conditions, has been proven effective to support winter road maintenance by improving safety, mobility, and efficiency. Although the geographic information systems are being widely applied for facility siting, traditional practices of sitting RWIS stations still heavily rely on the experiences of maintenance and operation personnel, which is time-consuming and subjective. This study develops a linear model to determine the optimal RWIS locations subject to three selection criteria: weather, traffic condition, and distance to existing RWIS sites, while considering practical constraints to satisfy specific requirements of various agencies (e.g., different weights of weather/traffic factors, various available budgets, etc.).
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Adverse weather significantly affects the safety and mobility of traveling public and the operations of road maintenance, especially during the winter season. It was estimated that on average, 24 % of all crashes are weather-related, resulting in the deaths of over seven thousand people annually [1]. Almost 20 % of the state department of transportation (DOT) maintenance budgets was used for winter road maintenance, and over 2.5 billion U.S. dollars has been spent on snow and ice control operations each year [2].
Accurate and timely weather and pavement surface information, which enables the capability of pro-active responses to roadway incidents, is therefore vital to reduce weather-related accidents and increase the effectiveness of road maintenance. During the last few decades, many states have deployed the road weather information system (RWIS) to capture weather and monitor road surface information. The data collected from RWIS stations could be applied to assist road maintenance decisions for snow and ice control operations. Thus, costs of staffing, material/chemicals and equipment, degradation of the surrounding environment, corrosion effects, and infrastructure damage may be significantly reduced [3–6].
The state DOT could benefit from the RWIS application not only by means of improving road safety and mobility, but also reducing maintenance cost. Analyses showed that the benefit–cost ratio of RWIS ranged from 2:1 to 10:1 [3, 5, 7]. For example, RWIS saved the state of Utah $2.2 million each year, which was 18 % of the annual winter maintenance budget in labor and material costs for snow and ice control activities [8].
ARWIS station could be characterized as ‘regional’ or ‘local’ based on its associated geographic and weather conditions [9]. A regional site would be placed in a location so as to represent general weather condition for a large area, while a local site would be placed in a spot-specific location of interest, such as historically cold locations prone to standing water or slippery conditions. Therefore, different criteria should be applied to determine the locations of regional and local sites. In this study, the optimization analysis focuses on regional stations, and the objective is to determine the optimal number and locations of stations, considering some practical user-defined criteria such as budget and station distance constraints.
Geographic information systems (GIS) have been widely applied in the facility siting and have proven to be a capable tool in assisting facility planning [10–13], which significantly enhances location planning and decision making [14]. ArcGIS 10.0 [15] is applied in this study to provide and gather required data and display the optimization results. To test the model applicability, a case study in New York State (NYS) is conducted, in which the candidate sites were identified along major highways based on various weather and traffic conditions.
2 Literature review
The planning and deployment of RWIS used to involve challenging and complicated processes. Traditional planning relied much on the experience of maintenance and operation staff, which focused more on local sites where adverse weather (i.e., snow and ice) caused safety concerns at problematic locations and sometimes made the selection of priority locations subjective and time-consuming. A study among 13 state DOTs [16] indicated that the deployment of RWIS was seriously impeded by lack of standards and available budget. Although a RWIS environmental sensor station siting guidelines [9] was developed, it focused more on individual stations than network planning. Very little research was found in optimizing RWIS considering heterogeneous road surface and weather conditions.
Planning RWIS may begin with identifying candidate sites via interviewing road maintenance and operation staff, and residence engineers. The suitability of each site may be evaluated against a set of criteria. A previous study conducted in Alaska [17] indicated that the evaluation criteria can be developed by gathering roadway, meteorological, and engineering perspectives; however, they were descriptive and required lots of inputs from key personnel. Alternatively, site evaluation can be conducted using criteria from the perspectives of natural environment (e.g., regional meteorology, topography, and vegetation) and operational features (e.g., highway networks, collision statistics, and traffic volume) [18]. The evaluation process included validating candidate sites and assessing the site suitability. Although the assessment was logical, the accuracy is highly dependent on the experience of maintenance staff.
Facility siting with GIS has been applied in a number of fields, which always involves multiple candidate sites, various constraints, and multiple objectives. For example, Liu et al. [19] optimized the siting of fire stations using GIS and a heuristic algorithm. Garcia-Palomares et al. [20] identified the optimal locations of bike stations within the environment of GIS. Farhan and Murray [13] proposed a multi-objective spatial optimization model for locating park-and-ride facilities, which compared the optimal sites with and without existing facilities. To evaluate the feasibility of potential landfill sites, Mahini and Gholamalifard [12] applied a weighted linear combination method in a GIS environment, which was characterized by tradeoff among the evaluation factors.
In related to siting the RWIS stations, however, few studies have been focusing on developing a procedure to optimize RWIS sites. Eriksson and Norrman [21] analyzed the locations of RWIS stations based on a slipperiness index, which was developed by combining several meteorological variables. Kwon and Fu [22] proposed a framework to evaluate possible locations for deploying RWIS, in which weather (i.e., variability of surface temperature, mean surface temperature, and precipitation) and traffic (i.e., traffic volume, accident rates, and highway type) factors were considered. The existing sites were used to evaluate the optimal results generated from different combinations of pre-defined factors. However, the potential sites were ranked without considering other factors, such as user needs on the deployment of criteria and practical constraints (e.g., relative importance of factors, locations of existing sites, etc.).
The contributions of this study are threefold. First, in contrast to previous planning of RWIS network which mainly focused on local sites, the proposed approach is applied to optimize regional sites for state wide road weather monitoring and forecasting. Second, a survey was conducted for determining the feasible RWIS sites, evaluation factors, and the associated factor weights. Therefore, the unique needs and locations of RWIS stations per jurisdiction could be integrated in the optimization process. Third but not the least, for practical RWIS planning and deployment, the proposed model also considered traffic condition and the constraints of available budget and existing weather stations into the optimization processes.
3 Methodology
To determine the optimal RWIS locations which yield the maximum total score subject to budget and site distance constraints, a linear model consisting of an objective function and a set of constraints is developed. In supporting winter road maintenance, the weather and pavement surface temperatures of heavy traffic routes shall be collected and monitored constantly to ensure road safety based on timely decision making in salt spreading and snow plowing.
Let I be a set of candidate sites and x i is a binary variable to represent the decision for siting a station at location i, where i ∈ I. Thus,
The objective total score function denoted as S is the weighted sum of all site scores. Previous studies [17, 18] suggest that the RWIS sites should be located in the area experiencing severe weather and heavy traffic conditions. In this regard, the average annual snowfall accumulation (AASA) can be considered as an index of winter weather severity [23], while the annual average daily traffic (AADT) can be used to represent traffic conditions. For planning a RWIS network, the distance to the existing RWIS stations (DIST) is also an important factor for determining new sites. Therefore, AASA, AADT, and DIST are employed for determining the score of each candidate site.
Let \(s_{{w_{i} }} , \, s_{{t_{i} }} , \, \text{and} \, s_{{d_{i} }}\) represent the scores of AASA, AADT, and DIST, respectively, of site i, and the associated weights are denoted as \(\alpha_{w} , \, \alpha_{t} ,{\text{ and }}\alpha_{d}\). Therefore, the objective total score function for all site can be formulated as
The total available budget, if there is, clearly is a constraint which limits the number of optimal sites. Note that, the selected sites may incur different costs of installation and maintenance depending on the required sensor types, the availability of power and communication services, and the proximity to staffed facilities. To this end, the budget constraint could be formulated as
where \(c_{i}\) is the cost of site i (i.e., the sum of initial installation cost and annual maintenance cost) and \(U\) represents the total budget.
According to FHWA’s siting guidelines, the spacing between the RWIS sites ranges between 32 and 50 km. Therefore, two constraints are formulated, considering the distance from a new station to adjacent stations (i.e., both existing and new stations). Equation (4) defines that the distance between any two optimal sites should be longer than the recommended distance denoted as D, and Eq. (5) ensures that the distance from an optimal site to the nearest existing site longer than D.
where \(d_{ij}\) is the distance between sites i and j; \(d_{ir}^{\prime}\) is the distance from site i to the nearest existing RWIS site. Note that R is a set of existing sites and r is an index of a site.
As discussed earlier, the regional sites are designed to provide road surface conditions and weather observations for a large area, which should be located on flat terrain to minimize local weather effects. Therefore in the proposed model, the area coverage designated to a candidate site is determined based on the spatial weather variability by means of the standard deviation (Std) of AASA.
As a cell with a resolution of 1.6 by 1.6 km centered in a specified neighborhood (9 cells in this example) as shown in Fig. 2, the Std of AASA denoted as \(\sigma\) can be calculated by Eq. (6).
where n is the number of cells, \(V_{k}\) is the AASA of cell k, and \(\mu\) is the mean AASA of all cells in the neighborhood (Fig. 1).
Considering the recommended RWIS site spacing of 32 km, a rectangular neighborhood shape with a side length of 32 km around each candidate site is selected to calculate the representativeness of that site. A threshold of Std denoted as \(B\) can be applied via Eq. (7) to ensure that each optimal site can properly present regional weather condition.
where \(\sigma_{i}\) is the AASA Std of site i. Finally, the proposed model consisting of an objective total score function and a set of constraints can be developed and formulated as
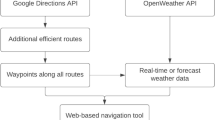
As illustrated in Fig. 2, a five-step procedure is executed to process collected data, generate required inputs, and then optimize the RWIS sites. The characteristics of candidate sites are quantified and reclassified into comparable values. Based on the pre-defined factor weights, the score of each site can be calculated. Then, a number of sites can be quantitatively optimized, subject to practical constraints.
A five-step procedure is developed to determine the optimal locations for deploying RWIS sites and explained below:
-
Step 1 Identify candidate sites and evaluation factors. Since the needs and requirements for RWIS stations will vary by jurisdiction, the personnel suggestions are valuable for cost-effective decision. For example, if an RWIS site is established at the location with available power sources and infrastructure, the cost of RWIS deployment will be significantly reduced. Therefore, the user needs and requirements for planning RWIS should be realized at the beginning of this study, which can be achieved by interviewing key personnel, so that the feasible RWIS sites, the evaluation factors, and the associated weights can be determined.
-
Step 2 Data collection. After determining key factors and weights, the data associated with each factor should be collected for evaluating candidate sites. In this study, three factors (i.e., AASA, AADT, and the locations of existing RWIS) were identified in Step 1 and the data for them are collected for analysis.
-
Step 3 Process data in ArcGIS. AASA, AADT, and DIST associated with the candidate sites are determined in this step. Then, the candidate sites are classified into 10 equal groups based on percentiles and assigned with scores running from 1 to 10 corresponding to the lowest to the highest score groups, respectively. To determine the weather, traffic, and distance information of the candidate sites, the input data are processed by the following steps:
-
(a)
Overlay the candidate site locations onto the highway network with AADT information, and thus the AADT associated with each site can be determined.
-
(b)
Since the original AASA data is station-based (i.e., locations of weather stations), the inverse distance weighting method [24] is applied to interpolate that data for the whole study region. By overlaying the candidate site locations onto the interpolated AASA data, the AASA associated with each site can be determined.
-
(c)
The Euclidean distance from each candidate site to the nearest existing site is calculated in ArcGIS, and the DIST attributed to every site can be determined.
-
(a)
-
Step 4 Calculate the scores of candidate sites. The total score of each site is calculated based on weighted sum of the scores generated from Step 3. A site with a higher score would be deemed as a more favorable site based on the defined factors.
-
Step 5 Optimize RWIS sites. In this step, the budget constraints and the minimum accessible distance between stations [Eqs. (4) and (5)] will be integrated, so that practical situations could be taken care of in the developed optimization model [Eq. (3)].
4 Case study
The purpose of this section is to test the proposed model applicability with the data collected in the State of New York (excluding New York City) where 386 candidate sites were arbitrarily selected based on weather and traffic conditions. There are 31 NYSDOT’s RWIS stations located in the study region. Three factors discussed earlier, including AASA, AADT, and DIST, are applied for determining the scores of the candidate sites. The weights associated with these factors in the analysis are assumed identical, meaning equally important, and the sensitivity of each factor to the optimal solution is analyzed and discussed in this section.
4.1 Model inputs
The model inputs applied to optimize RWIS sites include the following:
-
(a)
The locations of candidate sites, which are selected and assigned with latitude/longitude information in ArcGIS.
-
(b)
NYS boundaries, which are collected from U.S. Census Bureau [25, 26].
-
(c)
AASA data, which are collected from National Climatic Data Center [27].
-
(d)
NYS highway network with AADT information, which is collected from NYSDOT Traffic Data Viewer [28].
-
(e)
The locations of existing RWIS sites, which are collected from Meteorological Assimilation Data Ingest System [29].
The total score of each candidate site, which is the weighted sum of the scores associated with AASA, AADT, and DIST, is applied to rank the sites in a descending order (see Fig. 3 ).
AADT associated with NYS highway system is shown in Fig. 4, where interstate highways experiencing high traffic volumes are represented by bold brown lines. A sample map of candidate sites with roadways is provided in Fig. 5. The geographic distribution of AASA is represented in Fig. 6 showing that severe weather conditions exist in the west and north-central of NYS. Figure 7 represents the boundaries of NYSDOT regions.
4.2 Optimal solution
The installation and maintenance costs associated with the candidate sites may vary, depending on the accessibility of sites to maintenance yards, the availability of communication and facilities, and different requirements for sensors of RWIS sites. Due to limited budget for which most State DOTs are experiencing, a maximum of 50 new sites is assumed in the case study. The sites were optimized with LINGO 9 [30] and displayed in ArcGIS 10.0 (see Fig. 8). Of all the optimal sites (shown in blue square symbol), 60 % are located on the NYS highways, 30 % on the interstate highways, and 10 % on US highways. It is also noticed that half of the optimal sites fall in the area where the average annual snowfall accumulation is over 80 inches, and some of the sites recommended by the key personnel via survey are part of the optimal sites.
Table 1 illustrates the number of the existing and optimal sites and the associated densities (i.e., km2/station) from regions 1 through 10. The existing densities of RWIS sites in the regions are significantly fluctuated; for instance, the density is around 1,000 km2/station in region 6, but almost 23,000 km2/station in region 7. With such limited number of RWIS stations, it is hard to conduct statewide road weather monitoring and forecasting. After adding the optimal sites, the new RWIS stations fill the gaps of the existing network, and improve the coverage of weather forecast of the network. All the regions, except region 6, have new sites. Regions 1, 2, 5, and 7 have the highest increment—8 new sites in each region. The new densities get closer among most regions, which are in the range of 1,000–1,800 km2/station.
The combined effects of three factors (weather, traffic, and existing sites) contribute to the distribution of optimal sites. For example, region 6 has a significant amount of existing sites; therefore, no candidate sites in this region are presented in the optimal results. Conversely, many optimal sites are located along the major highways in regions 5 and 7 because of more adverse weather conditions and fewer existing sites.
5 Result analysis
5.1 Representativeness of regional weather
Considering the FHWA recommended distance between two RWIS sites (i.e., 32 km), the weather variability within 16 by 16 km around the optimal sites are generated to evaluate site representativeness, which is denoted as the Std of AASA in this study.
Figure 9 shows the distribution of AASA Std across the NYS. The results indicate that about half of the optimal sites fall in the area where the Std of AASA is smaller than 7.5 cm, and 80 % are within 0–11 cm; some of the optimal sites are located in the area with high AASA Std (i.e., high weather variability). If regional weather forecasting is deemed as a more important factor while allocating RWIS sites, the threshold for the weather variability should be investigated to ensure site representativeness during the optimization process.
5.2 Factor weights
While evaluating the influential factors for locating RWIS stations, one may regard monitoring pavement surface condition as essential while others may consider forecasting regional weather more important. This issue can be solved by surveying the RWIS users. In this analysis, three scenarios are analyzed based on three sets of factor weights (see Table 2), which result in varying optimal solutions:
-
Scenario 1 Default weights of weather, traffic, and distance of existing RWIS sites are identically equal to 1, assuming that these factors are of equal importance in the site decision.
-
Scenario 2 If monitoring pavement surface condition is vital in the area with heavy traffic volume, the importance of traffic factor should be more emphasized than other factors while locating RWIS sites. Thus, the weights setting for these three factors are high weight for traffic (2), and low weights for weather (0.5) and distance to existing RWIS sites (0.5).
-
Scenario 3 If more concerns are placed on monitoring and forecasting weather conditions, weather should be given a higher weight. Thus, the weights of the factors are high weather weight (2), and low weights for traffic (0.5) and distance to existing RWIS site (0.5).
The results show that more sites with high AADT are preserved under Scenario 2, as opposed to those under Scenario 1. The shift of optimal sites into heavy traffic roadways can be observed in Fig. 10, where more sites are located in the interstate highway segments—35 % of new sites are located on interstate highways compared to 30 % under Scenario 1.
Although most locations for optimal sites are the same, more sites experiencing severe weather conditions are preserved when a high AASA weight is set in Scenario 3 (see Fig. 11). For instance, the minimum AASA of optimal sites is 94 cm, compared to 66 cm under Scenario 1 and 69 cm under Scenario 2.
6 Conclusions
This paper proposes a general framework of applying GIS to optimize regional RWIS sites based on the pre-defined criteria. Within this framework, it is very effective to determine optimal sites by integrating traffic and regional weather conditions. While this study mainly focuses on developing an optimization model and solution framework, more practical conditions, such as administration factors (e.g., regional support and training, willingness to adopt the technology, or leveraging investment), should be considered while implementing this model.
The case study demonstrates a preliminary application of the proposed methodology. With the assumed locations of candidate sites and factor weights, this model is applied for conducting scenario-based analysis. Although three major factors are currently being considered, the model is capable of integrating other criteria (e.g., population density, accident rates, and availability of power/communication sources) and constraints (e.g., representativeness of regional weather or traffic volume/roadway functional classification constraints). Several issues will be considered in the immediate extension of this study:
-
(1)
Other weather factors (e.g., land surface temperature, number of weeks with transition temperature, and duration of freezing rain) and traffic factors (e.g., accident rate and population density) that might affect the locations of RWIS sites will be considered in the optimization process.
-
(2)
The microclimates will dictate some of site inter-distances as being much closer than 32 km (which is recommended by FHWA siting guidelines), while the stations in many typical zones can be spaced further apart. Therefore, the impact of weather variability—analyzed from the combination of all the weather parameters listed in (1)—on the optimization of RWIS sites will be further investigated.
-
(3)
The RWIS implementation costs and the associated benefits (e.g., travel time, accident cost, and winter maintenance cost savings) may vary among sites. Therefore, incorporating a life-cycle cost–benefit analysis in the optimization process is essential to the development of a statewide RWIS network.
References
FHWA (2013) How do weather events impact roads? www.ops.fhwa.dot.gov/weather/q1_roadimpact.htm. Accessed. 20 Dec 2013
Rall J (2010) Weather or not? state liability and road weather information systems. National Conference of State Legislatures
Boselly SE (2001) Benefit/Cost Study of RWIS and Anti-icing Technologies. National Cooperative Highway Research Program
Pisano PA, Goodwin LC, Stern AD (2006) U.S. Road weather management program: sensor siting and weather information integration projects. In: Proceedings of 13th SIRWEC conference, Turin
Ye Z, Strong C, Fay L, Shi X (2009) Cost benefits of weather information for winter road maintenance. Final report for Iowa Department of Transportation. Western Transportation Institute
Greening K, Johns D, Bridge P, Koeberlein R (2012) A study to determine the effects of employing a well maintained RWIS network on accident rates on major highways in the US state of Idaho. In: Proceedings of 16th SIRWEC conference, Helsinki
Pederson BJ, Christensen FK, Johansen KS (2008) Cost effective monitoring of RWIS: communication and maintenance. In: Proceedings of 14th SIRWEC conference, Prague
ITSJPO (Intelligent Transportation Systems Joint Program Office) (2009) Investment opportunities for managing transportation performance through technology. U.S. Department of Transportation
Manfredi J, Walters T, Wilke G, Osborne L, Hart R, Incrocci T, Schmitt T, Garrett VK, Boyce B, Krechmer D (2008) Road Weather Information System Environmental Sensor Station Siting Guidelines, Version 2.0. FHWA, Washington, DC
Li X, Yeh AG (2005) Integration of genetic algorithms and GIS for optimal location search. Int J Geogr Inf Sci 19(5):581–601
Murray AT, Tong D (2007) Coverage optimization in continuous space facility siting. Int J Geogr Inf Sci 21(7):757–776
Mahini AS, Gholamalifard M (2006) Siting MSW landfills weighted linear combination methodology in a GIS environment. Int J Environ Sci Technol 3(4):435–445
Farhan B, Murray AT (2008) Siting park-and-ride facilities using a multi-objective spatial optimization model. Comput Oper Res 35:445–456
Murray AT (2010) Advances in location modeling: GIS linkages and contributions. J Geogr Syst 12(3):335–354
ESRI (2011) ArcGIS desktop: release 10. Environmental Systems Research Institute, Redlands
Castle Rock Coaqnsultants, Inc. (2002) Road weather information systems (RWIS) data integration guidelines. Portland, OR
Sullivan J (2004) Road weather information system phase II & IIB. Alaska Department of Transportation
Pinet MF, Lo A (2003) Development of a Road Weather Information System (RWIS) Network for Alberta’s National Highway System. Presented at 2003 annual conference of the Transportation Association of Canada, St Johns Newfoundland
Liu N, Huang B, Chandramouli M (2006) Optimal siting of fire stations using GIS and ANT algorithm. J Comput Civil Eng 20(5):361–369
García-Palomares JC, Gutiérrez J, Latorre M (2012) Optimizing the location of stations in bike-sharing programs: a GIS approach. Appl Geogr 35(1):235–246
Eriksson M, Norrman J (2001) Analysis of station locations in a road weather information system. Meteorol Appl 8(4):437–448
Kwon TJ, Fu L (2013) Evaluation of alternative criteria for determining the optimal location of RWIS stations. J Mod Transp 21:17–27
Mewes JJ (2011) Mapping weather severity zones. Final report for clear roads pooled fund study
Shepard D (1968) A two-dimensional interpolation function for irregularly-spaced data. In: Proceedings of the 1968 23rd ACM National Conference, pp 517–524
U.S. Census Bureau (2013) www.census.gov/geo/maps-data/data/tiger.html. Accessed 21 Apr 2013
NYSDOT Regional Offices (2013) www.dot.ny.gov/regional-offices. Accessed 12 Dec 2013
NOAA (1981–2010) Climate normals. www.ncdc.noaa.gov/oa/climate/normals/usnormals.html. Accessed 20 Dec 2013
NYSDOT Traffic Data Viewer (2013) www.dot.ny.gov/tdv. Accessed 20 Dec 2013
Meteorological Assimilation Data Ingest System (MADIS) (2013) https://madis-data.noaa.gov/public/sfcdumpguest.html. Accessed 2 Apr 2013
LINDO Systems Inc (2004) Lingo user’s guide. LINDO Systems Inc., Chicago
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Zhao, L., Chien, S.I., Liu, X. et al. Planning a road weather information system with GIS. J. Mod. Transport. 23, 176–188 (2015). https://doi.org/10.1007/s40534-015-0076-0
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40534-015-0076-0