Abstract
The skip-stop operation strategy (SOS) is rarely applied to Chinese urban rail transit networks because it is a simple scheme and a less universally popular transportation service. However, the SOS has performance advantages, in that the total trip time can be reduced depending on the number of skipped stations, crowds of passengers can be rapidly evacuated at congested stations in peak periods, and the cost to transit companies is reduced. There is a contradiction between reducing the trip time under the SOS and increasing the passengers’ waiting times under an all-stop scheme. Given this situation, the three objectives of our study were to minimize the waiting and trip times of all passengers and the travel times of trains. A comprehensive estimation model is presented for the SOS. The mechanism through which the trip time for all passengers is affected by the SOS is analyzed in detail. A 0–1 integer programming formulation is established for the three objectives, and is solved using a tabu search algorithm. Finally, an example is presented to demonstrate that the estimation method for the SOS is capable of optimizing the timetable and operation schemes for a Chinese urban rail transit network.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
China is rapidly developing its urban rail transit (URT) networks. The Beijing URT network alone provides nearly 10,000,000 person-trips a day. The development of URT networks is increasing the trip distances and travel times of passengers on the networks. Consequently, there is a pedestrian congestion due to a drop in the service levels and increasing security risks. This study investigates the skip-stop operation strategy (SOS) as a means of solving these problems. The SOS can reduce the trip time of most passengers, while also improving the comfort and level of service, which can attract new passengers. More importantly, the problem of unexpected passenger flows needs to be solved for the complex system of popular urban transportation. In particular, the SOS has the ability to evacuate congested stations and temporarily add trains. In other words, the SOS increases the operating speed and the capacity of the URT system while also reducing trip times and the crowding of trains. However, the main issue relating to the SOS is the increased waiting time for passengers intending to board or alight at skipped stations. This is a source of confusion for passengers but the confusion could easily be resolved by providing in-depth information through, for example, broadcasts, guiding signs, and videos. With this background, the present study focuses on minimizing the travel costs for passengers and running trains.
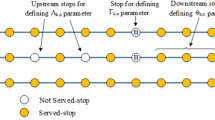
Schemes of the SOS can be classified as either serial or parallel. Parallel schemes demand two or more tracks, allowing different services, such as local trains, rapid trains, and express trains, to coexist (see Fig. 1). These trains are spatially isolated and do not affect each other. Local trains stop at every station, while rapid trains may skip several stations and express trains only stop at major stations. Parallel schemes are thus able to improve transportation capabilities and satisfy the time demands of different passengers. We understand that parallel schemes were introduced to the New York Metro system in the 1950s. Since 2007, SOSs have been implemented in Santiago and for osaka urban rail, Japan. Users quickly adopted the extra services. However, this study focuses on serial schemes of a one-way single-track URT network.
A key component of urban transit operation and management is how to determine arrival and departure times according to passenger demand [1]. Daganzo made an alternative attempt to quantify the operational benefits of skip-stop operation [2]. Freyss tackled the problems of skip-stop operation already described in the literature (Vuchic, 1973, 1976, 2005) [3]. Cost functions have been developed for an all-stop operation, and a continuous approximation approach has been presented [4]. For random bus travel times, stop-skipping has been formulated as an optimization model minimizing the weighted sum of three objectives [5]. Even though a metro network has not yet been established, SOS has still been used to optimize the operation of travel utilities and the provision of convenient trips, such as in the case of the Singapore Metro [6].
The SOS may notably affect passengers when either their stations of origin or their stations of destination are skipped, at which point they have to wait for at least one more train departure interval (hereafter referred to as the headway). To realize the greatest transportation capacity, we assumed that the timetable scheme had a parallel train configuration. The mean speeds of all trains were assumed to be equivalent, which is an assumption that can also be applied to all-stop schemes. Moreover, the total trip time and total number of decelerations and accelerations must affect the operating costs of a metro company. Many previous studies on the SOS focused only on reducing the journey or trip times of passengers, without considering costs to the company, for e.g., Li’s model [7]. Additionally, the time saved largely depended on the difference in headways between the all-stop and SOS schemes in Vuchic’s study [8], yet this may be unrealistic because the headways could be similar. To resolve these issues, a novel estimation method is presented in this paper.
The objective function of the model is a non-convex problem, which is known as an NP-hard (non-deterministic polynomial-time hard) problem. A tabu search algorithm was adopted to solve this problem.
2 Mathematical model
2.1 Assumptions and parameters
Even though the URT network in Beijing is strongly connected and has no skip-stop patterns, a studied train line, denoted as l, can reflect the essence of a skip-stop pattern. The aim of our study is to develop an estimation method for SOS operation that can be used to minimize the total cost to the passengers and companies. The methodology mainly focuses on a Chinese metropolitan URT network during peak hours. Without doubt, the method can also be applied to off-peak hours or the network of a mid-sized city. An SOS can relieve congestion at crowded stations, especially congestion resulting from unexpected passenger flows. Specifically, the method is applicable under the following assumptions which are discussed in detail later.
-
(i)
If train i skips station j, then it does not skip station j + 1; moreover, station j is not skipped by train i + 1.
-
(ii)
The timetable scheme has a parallel train configuration. Furthermore, trains are punctual according to the scheduled timetable.
-
(iii)
There are only two types of train, namely local trains and rapid trains. Express trains are not accessible at the stations leading up to the destination (see Fig. 1).
Assumption (i) is based on the serial scheme of the SOS. Passengers are assumed to have sufficient knowledge of the SOS or experience in using trains to recognize whether the trains they want to board skip stations. Assumption (i) ensures that passengers need not wait too long when a train they intend to board skips their desired station. Assumption (ii) guarantees maximum transportation capacity (see Fig. 2). Because of the serial scheme, it is unusual for a train to skip two or more consecutive stations, and it is not allowed in regular operation. This is expressed by assumption (iii).
The parameters of the method are introduced in Table 1.
2.2 Mathematical formulation
The mathematical formulation describing the SOS problem is introduced in detail. We assume that the dwell time is determined by trains skipping stations depending on the timetable, and does not depend on the arrival of unexpected passengers:
The departure time should be the arrival time plus dwell time:
where the arrival time A i,j is
Here, Di,j−1 is the departure time of train i from the previous stop j−1, r j is the travel time between the two stations, \(y_{i,j - 1} \cdot v_{\hbox{max} } /(432 \cdot \partial )\)is the acceleration time at station j–1, and \(y_{i,j} \cdot v_{\hbox{max} } /(432 \cdot \beta)\)is the deceleration time at station j. Without loss of generality, \(\frac{{v_{\hbox{max} } }}{432} \cdot \frac{1}{\beta } \cdot y_{i,j} + \frac{{v_{\hbox{max} } }}{432} \cdot \frac{1}{\partial } \cdot y_{i,j - 1}\)is the inevitable time loss consisting of both braking and acceleration losses as a result of stopping at one station. The parametric variables are determined experimentally for the URT line; the train travel time between two stations is measured with and without a train stopping in the context of performance. Fundamental statistical data obtained in experiments performed by Vuchic [8] indicate that a single train’s arrival time can be expressed sufficiently and empirically by Eq. (3).
The total number of passengers skipped by train i at station j is
The number of passengers boarding train i at station j is
The number of passengers alighting from train i at station j is
Accordingly, the number of passengers skipped by train i at station j, who expect to alight at station k, is
Conventional approaches simply set the parameters \(\xi\) and \(\eta\) as 0 and 100 %, respectively (i.e., \(S_{i,jk} = W_{i,jk} - W_{i,jk} \cdot y_{i,j} \cdot y_{i,k}\)), which implies that \(S_{i,jk} = 0\) if both the stations k and j are skipped and \(S_{i,jk} = W_{i,jk}\) if only station k or j is skipped. However, these parametric values are inappropriate because of the bounded rationality that passengers do not have full travel information of the SOS for the URT network. The variables \(\xi\) and \(\eta\) take values of 50 % in our study, which means that S i,jk = 0, if both the stations k and j are not skipped as given in Eq. (7). If the departing station j is skipped, then S i,jk = W i,jk . In particular, if k is similarly skipped, the result (S i,jk = W i,jk ) will lead to a circulation deadlock. This means that some passengers do not board train i because their station of departure is skipped. Sequentially, because the station of arrival is skipped by train i + 1, passengers do not board this train, which does not match reality. Normally, some 50 % of passengers traveling to a destination station skipped by a train in fact board the train, as evaluated from survey data. Because the skipping of the destination station prevents those passengers from alighting at their intended station, they alight at the station in advance or following their intended station to transfer to feed service buses or walking corridors. Here, W i,jk is the total number of passengers waiting at stop j expecting to alight at stop k:
When stations where passengers intend to board or alight are skipped, passengers will choose an optimal path with less transfer or a minimum trip time, such as by boarding the next train i + 1. The aim of our study was to develop a method with which the SOS improves train timetables to reduce the costs to passengers and metro companies. Evidently, there is a contradiction between reducing the trip time under the SOS and increasing the waiting time under the all-station scheme. The following section presents a mathematical method that solves the contradiction and establishes relevant constraints.
2.3 Objective function
Assuming passengers arrive at station j heading to station k at a constant rate \(\lambda_{j,k}\), the average waiting time for passengers at station j waiting for train i is denoted as \(\overline{w}_{ij} = h/2\)[9].
If station j is skipped by train i, passengers will need to wait for the next train i + 1. In this case, those passengers arriving at station j before the arrival of train i, denoted as S i,j , have a waiting time of h/2 + h. Hence, the total waiting time for the passengers taking trains i and i + 1 is
The total trip time for passengers boarding train i at station j and alighting at station k is \(\sum\nolimits_{f = j + 1}^{k} {(r_{i,f} + \frac{{v_{\hbox{max} } }}{432} \cdot \frac{1}{\beta } \cdot y_{i,j} + \tau_{i,j} \cdot y_{i,j} + \frac{{v_{\hbox{max} } }}{432} \cdot \frac{1}{\partial } \cdot y_{i,j - 1} } )\). Taking the summation for all trains, the travel time of all passengers is calculated as
Similarly, the total trip time of trains i and i + 1 is
These three objectives are addressed using the weighted sum method:
where c1, c2, and c3 are the weighting values for each objective. Furthermore, the first and last stations cannot be skipped; thus,
For instance, if two successive stations cannot be skipped, then a constraint is added:
During the URT operational period, the constraint that two successive trains do not skip the same station is expressed as
The formulation in Eq. (12) is a complex combinatorial-type problem. The objective function consists of a waiting time component and an onboard traveling time component, which are in conflict depending on the passenger demand matrices in reality. The optimal SOS is able to approximate the equilibrium of mining the total time by increasing the lower proportion of passengers’ waiting time to decrease the travel time, because some stations are skipped. Before the calculation, we qualitatively propose a hypothesis that the demands of passengers departing from and arriving at skipped stations are less. The next section explains the optimal estimation algorithm in detail.
3 Algorithm
The proposed model for SOS optimization is a complicated 0–1 mixed-integer programming problem. To date, traditional algorithms have not been suitable for finding an optimal solution to this problem, and we thus present a computational study of a parametric tabu search as a generic heuristic algorithm. For example, Liu [5] used a genetic algorithm incorporating a Monte Carlo simulation to solve the model of optimizing a bus stop-skipping scheme. Because the number of SOSs is 218 = 262,144 for a single line within 20 stations, the tabu search algorithm can be used to estimate the SOS for a Chinese URT network using Beijing Subway data.
The proposed model for SOS optimization is a complicated 0–1 mixed-integer programming problem. To date, traditional algorithms have not been suitable for finding an optimal solution to this problem, and we thus present a computational study of a parametric tabu search as a generic heuristic algorithm. For example, Liu [5] used a genetic algorithm incorporating a Monte Carlo simulation to solve the model of optimizing a bus-stop-skipping scheme. Because the number of SOSs is 218 = 262,144 for a single line within 20 stations, the tabu search algorithm can be used to estimate the SOS for a Chinese URT network using Beijing Subway data.
-
Step 0
(Initialization) The initial parameters of the algorithm are set. The initial solution is randomly generated according to the constraints (1–8) of the actual problem. At the same time, the tabu list is set at zero and the iteration number num = 0.
-
Step 1
(Setting the goal constraint) First, the goal time of the operation strategy for all stops is calculated; this serves as the maximum for the goal constraint. Iterative calculations num = num + 1 then begin.
-
Step 2
(Optimizing the feasible solution) According to a random search, a feasible solution is found and recorded as one of a number of solutions. Either the feasible solution is optimized for a better consequence, or, to avoid deviating too much from the existing solution, only two elements of the outcome matrix are changed to their alternate value (0 or 1).
-
Step 3
(Finding an optimal solution) To find an optimal solution, the solutions should be judged throughout N × M calculations until the solution cannot be updated.
-
Step 4
(Stopping the test) When the minimal objective function Z cannot be further reduced in the above steps, the matrix Y ij can be considered one of the optimal solutions. Finally, the problem of the SOS, as an NP-hard problem, is solved employing the tabu search algorithm.
4 Numerical simulations
4.1 Data settings
The SOS model and corresponding tabu search algorithm incorporating numerical simulations are verified in detail in this section. The simulation data were acquired from Line 1 of the Beijing Subway. There are 20 stations along this line, and Table 2 gives the OD passenger distribution for those stations. From the survey data in Table 1, we know the number of boarding and alighting passengers at every station, and the objective function can thus be calculated and outcomes updated (Table 2).
The dwell time is \(\tau \, {=}\, 0.5\,\hbox{min}\) in Eq. (1). The operating parameters, \(v_{\hbox{max} } = 70\)km/h, \(\partial = 0.9\) m/s2, and \(\beta = 1\) m/s2 obtained from the literature [10], can be used in Eq. (3). The headway h = 2.5 min. Because the SOS model can be applied to all trains, we compared the objective values of a random train with those for an all-stop strategy. To compute the numerical simulations concisely, we assume that only one train i adopts the SOS.
According to real survey data, the travel times between adjacent stations on Line 1 of the Beijing Subway are (in minutes)
The three weighting values in Eq. (11) are taken as c 1 = 1, c 2 = 1, and c 3 = 1. The weighting values for any follow-up study vary at different situations. When no station is skipped, the calculated result Z0 under the all-stop strategy is 3.2362 × 107 s, i.e., Y ij = 1 for all stations.
4.2 Simulation results
The algorithm was coded in Matlab R2008a and implemented on a personal computer having an Intel (R) Pentium(R) CPU running at 2.90 GHz with 4.00 GB RAM.
4.2.1 Optimal SOS
For the constraints of the SOS model, given by Eqs. (13) and (14), the simulation results are given in Table 3.
The corresponding value of the objective function is Z1 = 3.1876 × 107s = 8,854.4 h. Compared with the all-stop case (Z0 = 8,989.4 h), the total cost is reduced by 135 h, which indicates that the SOS can improve the operational performance of the URT line.
4.2.2 SOS model with different constraints
To solve SOS problems, the mathematical model is provided with a wide range of applicabilities. Considering a practical case, two or more stations might be skipped, such as when the Tiananmen East and Tiananmen West stations are skipped on the Chinese national day. When two or three stations are skipped successively, the results for the SOS model are as given in Tables 4 and 5, respectively. The total times (costs) are Z2 = 8,796.2 h and Z3 = 8,754.5 h.
Throughout these numerical simulations, the objective function cannot be optimized further because of the given constraints. If the stations can be skipped successively in the uncontrolled case, the objective value will be a minimum, which is 8.6103 h. However, 12 stations are skipped in this case, which is only discussed theoretically. Furthermore, these examples fully realize the three objectives.
4.3 Sensitivity analysis
The maximum speed, dwell time, and headway significantly affect the objective, and we thus need to analyze the three parameters for the sensitivity of the SOS model. To establish the trend of the function, we acquire a series of values to observe the changes in the total cost, which are shown in Figs. 3, 4, and 5. The objective is positively related to three parameters, namely the maximum speed, dwell time, and headway. Furthermore, the objective can vary 0.00145, 0.31, and 4.36 % on average when the maximum speed, dwell time, and headway change by 1 km/h, 1 s, and 1 min, respectively. Therefore, the most sensitive parameter, headway, affects the objective through the SOS model, which is important to the URT Operations Management Department.
4.4 Discussion
The simulations carried out in our study only considered the SOS for one train based on the train’s passenger demand matrix. On a continuous basis, the SOSs for subsequent trains may be determinate or stochastic depending on the passenger demands of the trains, which consist of the accumulated, abandoned passengers skipped by the upstream train, even when a subsequent train does not adopt the SOS. However, whatever strategies the downstream trains adopt is up to the operation authorities and empirical passenger situations, and we are able to generalize the operation strategies of all trains using our proposed estimation method.
5 Conclusions
SOSs are almost nonexistent for Chinese URT networks. However, URT operation companies in China face several problems, such as the arrival of unexpected, oversaturated passengers wanting to board trains and trains being delayed. With the intention of minimizing the objectives of the passengers’ total waiting and trip times and trains’ travel times, an SOS model was established and optimized for a Chinese URT network. The model analyzes the microcosmic time behaviors of passengers and trains in detail, and is applied to different situations. However, the NP-hard problem needs resolving, and a tabu search algorithm within a reasonable precision range was thus investigated. In simulations, the objective was calculated in a short time for each train and the SOS optimized the trip time. If stations can be skipped successively, the trip time can be further reduced. Finally, the results of a sensitivity analysis established that the maximum speed, dwell time, and headway are positively correlated with the objective. In addition, the shorter the headway, the better the objective is optimized. A numerical example was presented to fully explain this phenomenon. Future study will focus on exploring the three weighting values in Eq. (11) and whether the parameters in Eq. (7) are realistic.
References
Niu H (2011) Determination of the skip-stop scheduling for a congested transit line by bilevel genetic algorithm[J]. Int J Comput Intell Syst 4(6):1158–1167
Daganzo CF (2005) Logistics Systems Analysis, 4th edn. Springer-Verlag, Heidelberg
Yulong P, Shumin F (2006) Research on design speed of urban pedestrian crossing. J Highw Transp Res Dev 23(9):104–107 (in Chinese)
Transportation Research Board (2000) Highway Capacity Manual 2000[M]. National Research Council, Washington DC, pp 635–640
Liu Z, Yan Y, Qu X et al (2013) Bus stop-skipping scheme with random travel time[J]. Transp Res Part C 35:46–56
Zhichao C, Dewei L (2013) Inspiration from the human-oriented design and security operation of Singapore Metro [J]. Urban Rapid Rail Transit 2:138–142
Li Z, Rui S, Shiwei H, Haodong L (2009) Optimization model and algorithm of skip-stop strategy for urban rail transit[j]. J China Railw 31(6):1–8
Vuchic VR (2005) Urban transit[M]. Wiley, New York
Ceder A, Marguier PHJ (1985) Passenger waiting time at transit stops. Traffic Eng Control 26(6):327–329
2003 G B. Metro design specification [S] [D]. 2003. (in Chinese)
Acknowledgments
This work was financed by the National Basic Research Program of China, under project ID 2012CB725403.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
This article is published under license to BioMed Central Ltd. Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Cao, Z., Yuan, Z. & Li, D. Estimation method for a skip-stop operation strategy for urban rail transit in China. J. Mod. Transport. 22, 174–182 (2014). https://doi.org/10.1007/s40534-014-0059-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40534-014-0059-6