1 Introduction

At 14:28, May 12, 2008, a great earthquake measured Ms = 8.0 hit Wenchuan, Sichuan Province of China. According to field investigation, 53,295 km-long highways were badly destroyed in the earthquake [1]. In order to provide references for reconstruction and further research [2, 3], we have made a lot of field investigation to many highways in the earthquake area. The results of field investigation show that the dominant failure modes of embankments are lateral spreading, surface subsidence, collapse, and dislocation, as shown in Fig. 1.

Fig. 1
figure 1

Embankment slope landslide in Wenchuan earthquake

Full size image

Failure modes, mechanism, and sliding surface of earthquake-induced landslides are studied by means of field investigation and shaking table model tests. The earthquake-induced failure surfaces usually consist of tension cracks and shear which is different from gravity-induced failure surface made by shear zone only. Depth of dynamic sliding surface will be deeper along with the increase of peak ground acceleration, as shown in Fig. 2.

Fig. 2
figure 2

Sliding of road embankment body

Full size image

Because the stability of a slope is affected by geological and engineering factors, and many of the factors can not be obtained directly, we have to use uncertain method to deal with this kind of issues, such as fuzzy math [4], artificial neural network method [5], grey theory [6], support vector machine model [7], and extension method [8]. In these methods, the weight of each factor index directly determines the accuracy to a certain extent.

Catastrophe theory, which originated from the study of the French mathematician René Thom in the 1960s, becomes very popular due to the efforts of Christopher Zeeman [3] in the 1970s. It considers the special case where the long-run stable equilibrium can be identified with the minimum of a smooth, well-defined potential function (Lyapunov function) [9, 10].

In mathematics, catastrophe theory is a branch of bifurcation theory for study of dynamical systems and a particular special case of more general singularity theory in geometry as well. Bifurcation theory studies and classifies phenomena characterized by sudden shifts in behavior arising from small changes in circumstances, analyzing how the qualitative nature of equation solutions depends on the parameters that appear in the equation. This may lead to sudden and dramatic changes, such as the unpredictable timing and magnitude of a landslide [11].

Small changes in certain parameters of a nonlinear system can cause equilibria to appear or disappear, or to change from attracting to repelling and vice versa, leading to large and sudden changes of the behavior of the system. However, examined in a larger parameter space, catastrophe theory reveals that such bifurcation points tend to occur as part of well-defined qualitative geometrical structures. The main feature of the catastrophe progression method is that the weight of indices is not considered, which can avoid the effect of human subjective factor in practice [12].

In this article, the catastrophe progression method is used to evaluate the seismic stability of the embankment slope, and a reasonable result was achieved, indicating that the catastrophe progression method is feasible in predicting the seismic stability of embankment slope.

2 Key evaluation technique and steps of catastrophe progression method

In the catastrophe progression method, we first divide the evaluation system into sub-indexes, then normalize the control variables, and finally calculate the catastrophe affiliated functional value according to the complementary principle and non-complementary principle [13, 14]. The main evaluation steps are as follows.

2.1 Establishment of the hierarchy analysis model

First of all, an overall evaluation system is divided into sub-indices and all indices are grouped in accordance with the purpose of evaluation. In each hierarchy, the indices form a different catastrophe system. The weights of indices are not concerned, but the relative importance of each index is considered. Because the number of control variables could not exceed 4, the number of index in each hierarchy will not exceed 4 either.

2.2 Determination of catastrophe system classification for each hierarchy

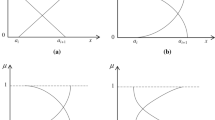
There are seven types of catastrophe systems, wherein the most four common types are folded catastrophe, cusp catastrophe, swallowtail catastrophe, and butterfly catastrophe. The potential functions are shown as follows [15, 16]:

Folded catastrophe:

$$ f_{1} (x) = x^{3} + ax. $$
(1)

Cusp catastrophe:

$$ f_{ 2} (x) = x^{ 3} + ax^{ 2} + bx. $$
(2)

Swallowtail catastrophe:

$$ f_{ 3} (x) = x^{ 5} + ax^{ 3} + bx^{ 2} + cx. $$
(3)

Butterfly catastrophe:

$$ f_{ 4} (x) = x^{ 6} + dx^{ 4} + ax^{ 3} + bx^{ 2} + cx. $$
(4)

In above equations, \( f_{i} (x) \) is the potential function of the state variable x, and a, b, c, and d are control variables of x.

2.3 Normalizing the control variables of the catastrophe model

Lack of proportionality in the indices can be eliminated using a standard transformation method so that the evaluation indices are dimensionless.

For the-larger-the-better indices can be calculated by the following functions:

$$ r = \frac{x}{{x_{ \hbox{max} } }}, $$
(5)

and for the-smaller-the-better indices can be calculated by the following functions:

$$ r = \frac{{x_{\hbox{min} } }}{x} ,$$
(6)

where \( x_{\hbox{max} } \) and \( x_{\hbox{min} } \) are the maximum and minimum value of the measured x, respectively.

If the values of x are within the range [0, 1], the measured values does not need to be normalized and can be directly used in the catastrophe progression computation.

2.4 Normalization formula

Let \( f(x) \) be the potential function of the catastrophe system, and the critical points of the potential function form an equilibrium surface according to the catastrophe theory. We can obtain the equation by calculating the first derivative of \( f(x) \), and obtain its singularity set by setting \( f''(x) = 0 \). The normalization formula is derived from the decomposition forms of the equation of the bifurcation point set. Different states of the control variables in the catastrophe system are then transformed into state variables using normalization formula. Based on catastrophe theory, the decomposition forms of the equation and normalization formulas of three conmen catastrophe systems are obtained as follows [17, 18].

For the cusp catastrophe system, the bifurcation point set equation is

$$ a = - 6x^{2} ,\quad{b = 8x^{3}} , $$
(7)

and its normalization formulas are

$$ x_{a} = \sqrt {\left| a \right|} ,\quad{x_{b} = \root{3} \of {\left| b \right|}}. $$
(8)

For the swallowtail catastrophe system, the decomposition forms of the bifurcation point set equation are

$$ a = - 6x^{2} ,\quad{b = 8x^{3}},\quad{c = - 3x^{4}} , $$
(9)

and the normalization formulas are

$$ x_{a} = \sqrt {\left| a \right|} ,\quad{x_{b} = \root{3} \of {\left| b \right|}},\quad{x_{c} = \root{4} \of {\left| c \right|}}. $$
(10)

For the butterfly catastrophe system, the decomposition forms of the bifurcation point set equation are

$$ a = - 10x^{2} ,\quad{b = 20x^{3}},\quad{c = - 15x^{4} ,d = 4x^{5}} , $$
(11)

and the normalization formulas are

$$ x_{a} = \sqrt {\left| a \right|} ,\quad{x_{b} = \root{3} \of {\left| b \right|}},\quad{x_{c} = \root{4} \of {\left| c \right|}},\quad{x_{d} = \root{4} \of {\left| d \right|}}. $$
(12)

In Eqs. (1)–(12), x a , x b , x c , and x d are values of x corresponding to a, b, c, and d.

2.5 Comprehensive evaluation through normalization formulas

Following the complementary principle and non-complementary principle, the catastrophe progression of each control variable can be computed from the initial fuzzy subordinate function. We find that each control variable of a system tends to reach the average value, so

$$ x = (x_{a} + x_{b} + x_{c} + x_{d} )/4 . $$
(13)

However, the non-complementary principle implies that the control variables cannot offset each other. Therefore, the smallest values of the state variables corresponding to the control variables are chosen to be state variable of the whole system. Based on hierarchical calculation, the value of the overall catastrophe subordinate function can be found in the same way [19, 20].

3 Application of catastrophe progression method to evaluate the seismic stability of embankment slope

3.1 Evaluation system of seismic stability of embankment slope

The control variables influencing the seismic stability of embankment slope are divided into three hierarchies, namely, the strength index, geometry characters of slope, and the earthquake effect. The indices of strength are internal frictional angle and cohesion force; the indices of geometry characters of slope include slope height, slope angle, and surface gradients; and peak acceleration and distance to fault are selected to be the influencing factors of earthquake. The overall evaluation system of seismic stability of the embankment slope is shown in Fig. 3.

Fig. 3
figure 3

Evaluation index system for seismic stability of embankment

Full size image

3.2 Determination of evaluation factors of embankment seismic stability

At present, the seismic fortification principle in the world is that the frame structure can achieve the seismic protective objective of no damage in small earthquake, repairable damage in moderate earthquake, and no collapse in severe earthquake. According to the above principle, the evaluation standard of the seismic damage to embankment slope is presented in Table 1. In addition, based on lots of tentative calculation, the critical values of catastrophe progression are also obtained [21, 22].

Table 1 Evaluation standard of the seismic damage to embankment slope [6]
Full size table

The embankments investigated include normal embankment and high fill embankment. In the high fill embankment, the surface gradient varies and crushed stones are the main filling material. The actual seismic damage to embankment can be described as in Table 2.

Table 2 Measured data for seismic stability of embankment
Full size table

3.3 Determination of utility function values of bottom factors

In order to illustrate the concrete application of the catastrophe method, we take sample 1 as an example. According to formulas (5) and (6), it is easy to get C1, C2, C3, C4, C5, C6, and C7 as follows:

$$ C_{ 1} = 3 8/ 3 8= 1,C_{ 2} = 10/ 1 4= 0. 7 1 4,C_{ 3} = 9/ 3 4= 0. 2 6 5,C_{ 4} = 10/ 1 5= 0. 6 6 7,C_{ 5} = 10/ 1 5= 0. 6 6 7,C_{ 6} = 0. 4 2/0. 4 2= 1,C_{ 7} = 1 7/ 1 7= 1. $$

The slope safety factor can be calculated by rigid limiting equilibrium method, and the catastrophe progression value is calculated by formulas (7)–(13).

Since the units of indexes are not the same, the data in Table 2 should be normalized. The utility function values of bottom factors and the catastrophe progression of the samples are calculated and shown in Table 3.

Table 3 Utility function values of bottom factors
Full size table

3.4 Result analysis

A comparison between the catastrophe progression and safety factor of embankment slope is shown in Fig. 4. We can see that the catastrophe progression and safety factor have an approximately similar change law: the safety factor increases (decreases) with the catastrophe progression value in a similar way. In addition, most of the safety factor values is over 1.2 and the catastrophe progression value over 0.8, which means that most part of the embankment is stable in Wenchuan earthquake except for the part collapsed. The result is in accord with field investigation.

Fig. 4
figure 4

The change law of catastrophe progression value and safety factor

Full size image

The value of catastrophe progression reflects the combination relationship of the influencing factors, which can be used to analyze the synthetic effect of the influencing factors with different combinations on the seismic stability of embankment slope, and thus find the unfavorable combinations. Moreover, based on the field investigation and statistics, the catastrophe progression being employed as a quantitative criterion could avoid the complicated calculation and uncertainty assumption of safety factor.

The catastrophe progression method does not need to assign a weight for each index as required by the fuzzy mathematical method, and hence can avoid the human subjectivity in determining the weights. Even so, subjectivity and fuzziness can not be eliminated completely from damage evaluation and description, thus resulting in some difference between the evaluation results and the actuality. From comparative analysis of the obtained results, however, the estimation model can meet for the demand of engineering practices on the whole.

4 Conclusion

In this article, we introduce the catastrophe progression method to evaluate the seismic stability of embankment, by selecting internal frictional angle, cohesion force, slope height, slope angle, surface gradient, peak acceleration, and distance to fault as evaluation indices. Each objective index is quantified and normalized without need to consider its weight. Compared with the traditional fuzzy mathematical method, the catastrophe progression method is simpler and can avoid the human subjectivity in determining the weights of indices. Comparative analysis of the on-site investigation results show that the method can evaluate the seismic stability of embankment with a high accuracy and therefore has an application potential in predicting the seismic stability of embankment.