1 Introduction

The design of shallow foundations is governed by settlements at serviceability limit state and bearing capacity at ultimate limit state. Mechanisms associated to the bearing capacity at ultimate limit state were investigated (Prandtl 1920; Terzaghi 1943) and empirical formulations for its estimation developed (Brinch Hansen 1970). The proximity of a slope has a great influence on bearing capacity, which is common for the analysis of foundations of retaining structures, bridge abutments, and transmission towers, and is usually materialized in terms of reduction factors decreasing its value. Meyerhof (Meyerhof 1957) proposed a chart to modify load bearing factors (see Eqs. 1 and 2), in terms of the foundation depth and the slope angle. This chart only estimates a small number of cases, being necessary to strongly use interpolation to adapt the chart to day-to-day cases. An alternative is to use the well-known empirical reduction factors (Brinch Hansen 1970; Vesic 1973) that affect the bearing capacity general expression (see Eq. 1). However, their definition is too simple, and they do not take into account the distance from the footing edge to the slope edge. This lack of consideration is also seen when using the Meyerhof (Meyerhof 1957) chart, by this way being these common approaches somewhat restrictive.

Kusakabe et al. (Kusakabe et al. 1981) used the upper bound theorem to analytically develop design charts which provide a global reduction factor of the foundation bearing capacity depending on the slope angle, slope height distance to the slope edge, and mechanical properties of the soil (cohesion and friction angle). Similar charts were proposed by Leshchinsky (Leshchinsky 2015) and Leshchinsky and Xie (Leshchinsky and Xie 2016) using the upper-bound limit state plasticity failure discretization scheme. Based on experimental tests, Castelli and Lentini (Castelli and Lentini 2012) yielded charts similar to the Meyerhof ones (Meyerhof 1957), i.e., modifying the load bearing factors, but considering more parameters (including distance to the slope edge and slope height), while Yang et al. (Yang et al. 2019) also produced such kind of charts but based on an analytical approach using the upper bound limit analysis. Recently, Mase et al. (Mase et al. 2023) conducted a numerical analysis to study the stability of embedded strip footings near a slope, while Shiau et al. (Shiau et al. 2023) and Parimi et al. (Parimi et al. 2023) studied the bearing capacity of footings close to or on a rock slope.

Earthquakes also have a negative effect on shallow foundations bearing capacity (Keawsawasvong et al. 2024; Thottoth et al. 2024; Petchkaew et al. 2023a, b; Hong-in et al. 2023). Richards et al. (Richards et al. 1993) indicated that earthquakes may induce seismic settlements in foundations due to loss of bearing capacity, performing the study by the application of analytical models based on the upper bound approach and assumed a seismic degradation of the soil strength and inertial seismic lateral forces to developed charts that provide seismic bearing capacity factors. Budhu and Al-Karni (Budhu and Al-Karni 1993) developed similar charts but based on the limit equilibrium technique. Dormieux and Pecker (Dormieux and Pecker 1995) showed that the seismic loads strongly affect the bearing capacity of a strip foundation on a cohesionless soil. Knappett et al. (Knappett et al. 2006) studied the mechanisms of failure of shallow foundations under earthquake loading based on a series of experimental tests conducted on a shaking table and compared their results with theoretical ones. Cascone and Casablanca (Cascone and Casablanca 2016) evaluated the seismic bearing capacity factors by using the method of characteristics, extended to the seismic condition by means of the pseudo-static approach. Conti (Conti 2018) used a pseudostatic approach and the upper bound theorem of limit analysis for obtaining a set of formulas for the computation of the seismic bearing capacity of strip footings resting on cohesive-frictional and purely cohesive soils. Hamrouni et al. (Hamrouni et al. 2021) conducted a reliability analysis of the pseudo-static dynamic bearing capacity of a strip footing using the finite difference numerical technique, comparing their results with analytical solutions.

The research regarding the bearing capacity of a foundation considering both the seismic action and the proximity of a slope was performed by Sarma and Chen (Sarma and Chen 1996) that used the limit equilibrium method to provide expressions of the seismic bearing capacity factors in terms of the slope angle, friction angle, and ground acceleration. Kumar and Rao (Kumar and Rao 2003) analyzed the problem using the method of stress characteristics and showed that bearing capacity factors reduce considerably with increase of the seismic action for different ground inclinations. Yamamoto (Yamamoto 2010) used the upper bound approach to develop charts for obtaining such factors. Castelli and Motta (Castelli and Motta 2010) studied the phenomenon by a limit equilibrium method and a pseudo-static approach, obtaining a series of factors to modify the static load bearing factors, while Georgiadis and Chrysouli (Georgiadis and Chrysouli 2011) used an upper-bound plasticity solution to yield empirical equations. More recently, Cinicioglu and Erkli (Cinicioglu and Erkli 2018) conducted a thorough parametric approach using the finite element method to obtain design charts for foundations placed near slope and affected by the seismic action, in the case of a pure cohesion soil (i.e., considering a null friction angle). Lai et al. (Lai et al. 2022) also studied footings close to slopes in cohesive soils and considering the seismic action, while Kumar et al. (Kumar et al. 2023) used various machine learning algorithms to predict the seismic bearing capacity of footings close to slopes.

In this paper, the influence of both the proximity of a slope and the existence of the seismic action are analyzed for a surficial strip foundation on a frictional ground. The seismic bearing capacity (Eq. 4) in this study is estimated in terms of a seismic slope coefficient which affect the classical solutions provided for the static case that could be applied to Eq. 1 (Brinch Hansen 1970). A parametric study is conducted, considering as input parameters the soil strength (friction angle), slope height, slope angle, seismic acceleration (pseudo-static seismic coefficient), foundation size, and its distance to the slope. The results of the parametric study are presented in the form of design charts that could be easily used for the analysis of seismic bearing capacity.

The finite element method (FEM) is used for the analysis, by that way allowing an easy change of geometry and boundary conditions. This allows taking into account a variation of the wide range of parameters considered. In total, the FE parametric study involves 960 models that enable to determine the failure mechanism, by that way analyzing the influence of different parameters on the mode of failure. Additionally, limit equilibrium method (LEM) is used to conduct 240 LE models for the preliminary analysis of the influence of the pseudo-static seismic coefficient on the safety factor of the slope without any load at their crest in order to determine the minimum slope angle necessary for its stability. The consideration regarding the interface between the soil and the surficial footing is represented by a rigid plate element with a rigid soil-footing interaction.

2 Methodology

2.1 Problem Definition

Load bearing capacity of a footing (\({q}_{ult}\)) represents the maximum load that a footing can transmit to the ground prior to the failure. The value can be theoretically obtained, without consideration of deformations, following the classical Brinch-Hansen (Brinch Hansen 1970) expression:

$${q}_{ult}=c{N}_{c}{s}_{c}{i}_{c}{d}_{c}+q{N}_{q}{s}_{q}{i}_{q}{d}_{q}+\frac{1}{2}\gamma B{N}_{\gamma }{s}_{\gamma }{i}_{\gamma }{d}_{\gamma }$$
(1)

where \(c\) is the soil cohesion; \(q\) is the existing load over the foundation plane; \(\gamma\) is the soil unit weight; \(B\) is the foundation width; \({N}_{c}\), \({N}_{q}\), and \({N}_{\gamma }\) are the load bearing factors, defined according to the expressions given in Eq. 2 (Prandtl 1920; Terzaghi 1943; Brinch Hansen 1970; Reissner 1924), and which solely depend on the soil friction angle, \(\phi\); \({s}_{c}\), \({s}_{q}\), and \({s}_{\gamma }\) are factors that take into account the shape of the foundation (for a strip footing, those are equal to 1.0); \({i}_{c}\), \({i}_{q}\), and \({i}_{\gamma }\) are factors that consider the inclination of load applied to the foundation (if load is applied normally, those are equal to 1.0); and \({d}_{c}\), \({d}_{q}\), and \({d}_{\gamma }\) are factors that take into account the depth of the foundation (for a footing placed at ground surface, those are equal to 1.0).

$${N}_{q}={e}^{\pi {\text{tan}}\phi }{{\text{tan}}}^{2}\left(45+\frac{\phi }{2}\right) ; {N}_{c}=\frac{{N}_{q}-1}{{\text{tan}}\phi } ; {N}_{\gamma }=1.5\left({N}_{q}-1\right){\text{tan}}\phi$$
(2)

For the case of a strip footing placed at ground surface with the load applied normally to the base of the footing, Eq. 1 is reduced to:

$${q}_{ult}=c{N}_{c}+\frac{1}{2}\gamma B{N}_{\gamma }$$
(3)

Besides, if the soil has no cohesion (pure granular soil), the term \(c{N}_{c}\) is neglected. This expression is widely used in geotechnical engineering, but it neither considers the problem of a footing resting on or near a slope nor the seismic action. Thus, the load bearing capacity of a footing on a granular soil taking into account the proximity of a slope and a seismic action (\({q}_{ult,se}\)) may be defined as shown in Eq. 4, considering the load bearing capacity \({q}_{ult}\) affected by a “seismic slope coefficient” \({\eta }_{se}\):

$${q}_{ult,se}={\eta }_{se}{q}_{ult}$$
(4)

Factors that control coefficient \({\eta }_{se}\) are the geometry of the footing and the slope and the seismic action defined by the pseudo-static coefficient. The geometry of the slope is defined by its height, \(H\), and the slope angle or inclination, \(\beta\), while the interaction between the footing and the slope depends on the distance from the footing to the slope. Slope height may be parametrized in terms of \(H/B\); similarly, distance from the foundation to the slope may be defined as \(\lambda \cdot B\), being \(\lambda\) the distance between the footing’s near edge and the crest of the slope normalized with \(B\).

Slope angle can also be normalized. Given a particular height, slope stability analyses (e.g., Taylor charts (Taylor 1948)) show that the maximum slope angle in a pure granular soil strongly depends on the soil friction angle. In other words, the same slope angle may be more demanding depending on the friction angle. Therefore, to take into account the mentioned aspects, the slope angle will be normalized by \(\beta\) = \(\frac{{\text{tan}}\phi }{FS}\), where \(FS\) is the static slope safety factor. Note that \(FS\) is only associated with the static performance of the slope without any load at its crest, not being related to the footing bearing capacity.

The seismic action can be considered by a pseudo-static approach by defining the horizontal and vertical acceleration seismic coefficients, \({k}_{h}\) and \({k}_{v}\) respectively, assuming that inertia forces of the structure and the slope are equal. Such seismic acceleration coefficients correspond to the ratio of seismic acceleration over gravitational acceleration (g = 9.81 m/s2). In the following, horizontal acceleration will be considered uniform throughout the whole ground model subjected to constant inertial forces and \({k}_{v}\) = 0.5·\({k}_{h}\), as is normally taken in any pseudo-static calculation in geotechnical engineering (Eurocode 2004; Wyllie 2017).

Thus, the “seismic slope coefficient” \({\eta }_{se}\) defined depends on six geometrical and geotechnical parameters defined by four normalized parameters according to Eq. 5:

$${\eta }_{se}=f\left(H/B,\lambda ,\frac{{\text{tan}}\phi }{FS},{k}_{h}\right)$$
(5)

Table 1 summarizes the values considered for different parameters involved into the analysis by FEM. Footing width \(B\) was set to a constant value of 2.0 m, while selected values for \(H/B\) were 1, 2, 3, and 4 (e.g., maximum slope height was 8.0 m) and magnitudes for \(\lambda\) were 0, 1, 2, 3, and 4 (e.g., value of 0 corresponding to the foundation resting at crest of the slope). By this way, it is considered that the footing is resting on surface without consideration of the embedment of the footing.

Table 1 Values for the different parameters involve into the analysis by FEM
Full size table

Three friction angle (\(\phi\)) values were considered, 30°, 35°, and 40°, being representative for three granular soil compaction cases: loose, medium, and dense. \(FS\) selected values were 1.1, 1.35, 1.6, and 2.0, which correspond to (i) \(FS\) = 1.1 adopted for being a value slightly higher than \(FS\) = 1.0 representing the strict static stability; (ii) \(FS\) = 1.35 as a value slightly higher than the one normally accepted for the slope stability when accounting seismic action by a pseudo-static approach; (iii) \(FS\) = 1.6 being a value slightly higher than 1.5, the value commonly accepted for static slope stability; and (iv) \(FS\) = 2.0 being a value considered high for any slope stability analysis. Those \(FS\) values yield the following approximate slope angles (\(\beta\)): (a) 27°, 23°, 20°, and 16° for \(\phi\) = 30°; (b) 32°, 27°, 23°, and 19° for \(\phi\) = 35°; and (c) 37°, 32°, 28°, and 23° for \(\phi\) = 40°. Horizontal acceleration seismic coefficient (\({k}_{h}\)) considered in the analysis are 0.1, 0.2, 0.3, and 0.4 (g). Therefore, the total number of combinations is equal to 960.

A series of additional parameters are needed to define different simulations conducted. As unit weight (\(\gamma\)) was not expected to have an important influence in the problem studied, this was assumed as a fixed parameter equal to 20 kN/m3 in all cases (Cinicioglu and Erkli 2018). For the finite element analysis, Young modulus values (\(E\)) were defined by transforming \(\phi\) values into SPT ones using Wolff (Wolff 1989) expression and then applying the D’Appolonia et al. (D’Appolonia et al. 1970) relationship between SPT values (N) and Young modulus:

$$\phi =27.1+0.3N-0.00054{N}^{2} \left[in^\circ \right]; E=20+N [in MPa]$$
(6)

Note that SPT values obtained were 10, 28, and 47 for a friction angle \(\phi\) equal to 30°, 35°, and 40°, respectively, corresponding to a loose, medium, and dense granular soil, according to Terzaghi and Peck (Terzaghi and Peck 1948). Poisson ratio (\(\nu\)) was set to 0.3 in all cases while dilation angle (\(\psi\)) was defined as \(\phi\)–30° following Bolton (Bolton 1986).

Finally, to avoid numerical issues in the simulations conducted, a cohesion value equal to 1 kN/m2 was considered. That results in increasing \({q}_{ult}\) by 30 kN/m2, 46 kN/m2, and 75 kN/m2, for a friction angle \(\phi\) equal to 30°, 35° and 40°, respectively, that value being the one corresponding to the term \(c{N}_{c}\) (\({N}_{c}\) as defined in Eq. 2). However, this increment may be considered negligible, as shown later in Sect. 4.3. Besides, it should be noted that a cohesionless material is very rare in reality, since granular soils usually have even small amounts of fines.

2.2 Limit Equilibrium Model

A LE model based on the method of slices was conducted for each case under study. For this model, the commercial software Slide v.9 from RocScience was used. LEM considers only the static mechanical laws to define the stability of a soil slope, neglecting ground deformations. The method of slices is a common LEM which divides the sliding mass into several vertical slices which behave as rigid bodies. Normally, Mohr–Coulomb criterion controls soil failure. The method allows introducing loads on the slope crest. After applying force equilibrium on each slice, the resulting equation system requires additional hypotheses for its solution.

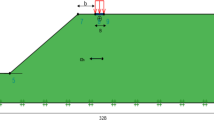
In this work, the Morgenstern-Price method (Morgenstern and Price 1965) was used to solve the static system. Figure 1 shows an example of the model developed. Geometry changed between models, depending basically on the slope height (defined by parameter \(H/B\)) and the slope angle (indirectly controlled by parameter \(FS\)). Seismic force was considered by the pseudo-static seismic coefficients \({k}_{h}\) and \({k}_{v}\).

Fig. 1
figure 1

LE model developed

Full size image

These models were built not to obtain the coefficient \({\eta }_{se}\), but as a preliminary analysis on how the combined parameters given in Table 1 may influence the value of the seismic safety factor of the slope without any load at its crest. Thus, these models analyze how the dynamic parameter \(FS\) is affected by parameters (\(H\), \(\phi , FS, {k}_{h}\)) without considering the slope-footing distance \(\lambda\) and the footing load itself. This means the performance of 192 models out of 960 mentioned above for FEM. Additionally, a LE model considering a null value of \({k}_{h}\) (i.e., no seismic action) was added for each case analyzed. So, in total, 240 LE models were run.

2.3 Finite Element Model

The commercial software RS2 v.11 from RocScience was used to build a FE model for running the 960 simulations defined in Table 1. Figure 2 shows a general scheme of models built. Similar to the LE models, geometry changed between models, depending on the slope height and angle. Left boundary was set to 12.5B from the slope toe. The slope area was mathematically defined by the slope height and angle. The foundation load is applied within the distance of (λ + 4)B from the slope crest. From that point, the right boundary was set at 5B. Dimension from the toe of the slope to the bottom of the model was established in 6B. Horizontal fixities (no movements allowed in X direction) were set at both sides of the model and total fixities (no movements allowed in X and Y directions) at the bottom of it.

Fig. 2
figure 2

FE model developed

Full size image

All models were meshed using 6-node triangular elements, with at least 100 nodes on the boundaries of the model. The model was divided in three meshing zones (Cinicioglu and Erkli 2018). Mesh below the footing extended a distance B and was the finest one (element length around 0.75); in this area, deformations are expected to be higher; besides, application of a horizontal acceleration normally results in shallower bearing failure mechanisms (Richards et al. 1993; Yamamoto 2010). The coarsest mesh corresponded to the area below the slope as well as the area located more than 3B form the edge of the footing, with element length around 3.00; those areas are not expected to have great relevance in the bearing failure mechanism and the bearing capacity. An intermediate zone between the previous ones was defined with an element length around 1.50.

Soil material was considered by an elastic model and a Mohr–Coulomb failure criterion, using the parameters defined in Table 1 for each case simulated. Surficial strip footing was represented by a rigid plate element with a rigid soil-footing interaction (i.e., interface strength coefficient equal to 1.0). The parameters corresponding to the footing involves Young modulus 30 GPa, Poisson ratio 0.2, and thickness 1.0 m.

An initial uniform load applied to the footing corresponds to a quarter of the maximum load determined by Eq. 3 (i.e., ultimate load for a flat surface with no seismic action). This initial load results in 75 kPa, 150 kPa, and 400 kPa for friction angles \(\phi\) equal to 30°, 35°, and 40°, respectively. That load was gradually increased by a 10% until reaching four times its initial value. This final load, when reached by FE model, approximately corresponds to the maximum footing bearing load defined by Eq. 3, i.e., 300 kPa, 600 kPa, and 1600 kPa for friction angles \(\phi\) equal to 30°, 35°, and 40°, respectively.

In all models, seismic action was introduced as a pseudo-static force, applied together with the footing load, and based on the seismic coefficients values given in Table 1.

3 Results

3.1 LEM

Figure 3 shows the results obtained in LE models in terms of the evolution of the slope seismic safety factor vs the horizontal seismic coefficient \({k}_{h}\) and the slope angle (defined in terms of the static safety factor \(FS\)), for given values of the ratio \(H/B\) and three friction angles \(\phi\) considered (30°, 35°, and 40°). Limit values for a seismic safety factor of 1.0 and 1.2 are highlighted; the first one corresponds to a strict stability while the second one to an intermediate value where a slope is considered stable in a typical seismic design (seismic safety factor is normally found between 1.1 and 1.3 depending on guidelines and regulations).

Fig. 3
figure 3

Seismic safety factor vs horizontal seismic coefficient \({k}_{h}\) and slope angle (defined in terms of the static safety factor \(FS\)) for given values of the ratio \(H/B\) and friction angles \(\phi\) (30°, 35°, and 40°). Gray dotted line corresponds to a seismic safety factor of 1.2

Full size image

The effect of the seismic action on the slope causes a clear reduction of the safety factor. This effect is similar for all friction angles. When having steep slope angles (which correspond to a static safety factor \(FS\) values of 1.1 and 1.35) and \({k}_{h}\) ≥ 0.2, the seismic safety factor is very low, even less than 1.0, indicating the slope is unstable. For this reason, it is not recommended to place the foundation beside the slope for \({k}_{h}\) ≥ 0.2 unless a gentle slope (corresponding to \(FS\) = 1.6 and 2.0) is planned for the design. For gentle slopes, the seismic safety factor shows higher values, although for \({k}_{h}\) ≥ 0.3 and ratio \(H/B\) ≥ 3, many of the slopes also display its low values. For \({k}_{h}\) = 0.4, seismic safety factor is close to 1.0 for gentle slopes with \(\phi\) = 40° and for very gentle slopes (i.e., \(FS\) = 2.0) for all studied values of \(\phi\).

Figure 4 shows the results in terms of the evolution of the slope seismic safety factor vs the horizontal seismic coefficient \({k}_{h}\) and the ratio \(H/B\), for given values of the slope angle (defined from the corresponding static safety factor \(FS\)) and the three friction angles \(\phi\) considered (30°, 35°, and 40°). Again, limit values for a slope safety factor of 1.0 and 1.2 are highlighted.

Fig. 4
figure 4

Seismic safety factor vs horizontal seismic coefficient \({k}_{h}\) and ratio \(H/B\) for given values of the slope angle (defined in terms of the static safety factor \(FS\)) and friction angles \(\phi\) (30°, 35°, and 40°). Gray dotted line corresponds to a seismic safety factor of 1.2

Full size image

As observed, the influence of \(H/B\) in the slope seismic safety factor tends to decrease as that ratio increases. Thus, given a slope angle and a \({k}_{h}\) value, the difference in the slope seismic safety factor when varying \(H/B\) is only significant for \(H/B\) < 3, being negligible for \(H/B\) ≥ 3.

3.2 Seismic Slope Coefficient \({\eta }_{se}\)

Figures 5, 6, and 7 show the results obtained in 960 FE simulations in terms of the seismic slope coefficient \({\eta }_{se}\), for friction angles \(\phi\) equal to 30°, 35°, and 40°, respectively. Each figure is presented for a fixed value of \(H/B\) (1, 2, 3, and 4) and \({k}_{h}\) (0.1, 0.2, 0.3, and 0.4), while showing the variation of \({\eta }_{se}\) for different values of \(FS\) (ranging from 1.1 to 2.0) and \(\lambda\) (ranging from 0 to 4). Note that for \({\eta }_{se}\) = 1.0, both the slope distance and the seismic action do not have effect on the footing bearing capacity (maximum bearing load can be achieved). Influence of different variable parameters on \({\eta }_{se}\) is described in the following sections.

Fig. 5
figure 5

Seismic slope coefficient \({\eta }_{se}\) for a friction angle \(\phi\) equal to 30°

Full size image
Fig. 6
figure 6

Seismic slope coefficient \({\eta }_{se}\) for a friction angle \(\phi\) equal to 35°

Full size image
Fig. 7
figure 7

Seismic slope coefficient \({\eta }_{se}\) for a friction angle \(\phi\) equal to 40°

Full size image

3.3 Failure Modes

As it is well known, shallow foundations can experience one of the three types of failure modes: (i) general shear failure; (ii) local shear failure; and (iii) punching shear failure. In the first type, the failure surface is fully developed, with the three common areas: a wedge active zone, just below the footing surface; two radial transition zones located next to the previous one; and two passive zones placed over the previous two and where the soil tends to heave. In a local failure, the passive zones are not totally developed. In a punching shear failure, only the wedge zone is fully developed, and the ground surface does not experience any bulging (Das and Sobhan 2017).

Figure 8 shows the failure modes exhibited by the slope-footing system in some of the FE cases studied in terms of shear plastic deformation, represented in the same range of values for the same value of \(\lambda\) for better analysis and comparison of studied cases. For the sake of brevity, only eight cases were selected to be displayed which are considered representative for the behavior of all studied cases of the surficial strip foundation close to the slope edge. Cases shown in Fig. 8 correspond to a ratio \(H/B\) = 3 and a static factor \(FS\) = 1.6. Figure 8 a to f correspond to the same seismic coefficient, \({k}_{h}\) = 0.1. Figure 8 a and b show the failure mode for the soil with a friction angle \(\phi\) = 30°, while the normalized slope-footing distance \(\lambda\) takes its two limit range values (i.e., \(\lambda\) = 0 and \(\lambda\) = 4, respectively). Figure 8 c and d show the same cases for \(\phi\) = 35°, while Fig. 8 e and f consider \(\phi\) = 40°. Figure 8 g and h correspond to \(\phi\) = 40° with the same kh and \(\lambda\) as in the case presented in Fig. 8 f but for different values of the seismic coefficient, \({k}_{h}\) = 0.2 and \({k}_{h}\) = 0.3, respectively, for its comparison.

Fig. 8
figure 8figure 8figure 8

Failure modes for cases with \(H/B\) =3 and \({\text{FS}}\) =1.60 (shear plastic deformation scale is the same for cases with the same \(\lambda\) value): a case \(\phi\) = 30°, \({k}_{h}\) = 0.1, \(\lambda\) = 0; b case \(\phi\) = 30°, \({k}_{h}\) = 0.1, \(\lambda\) = 4; c case \(\phi\) = 35°, \({k}_{h}\) = 0.1, \(\lambda\) = 0; d case \(\phi\) = 35°, \({k}_{h}\) = 0.1, \(\lambda\) = 4; e case \(\phi\) = 40°, \({k}_{h}\) = 0.1, \(\lambda\) = 0; f case \(\phi\) = 40°, \({k}_{h}\) = 0.1, \(\lambda\) = 4; g case \(\phi\) = 40°, \({k}_{h}\) = 0.2, \(\lambda\) = 4; h case \(\phi\) = 40°, \({k}_{h}\) = 0.3, \(\lambda\) = 4. Note: q represents the maximum bearing load reached

Full size image

As can be observed, when the footing is at the edge of the slope (\(\lambda =0\)) (Fig. 8a, c, e), this has a clear influence on the failure mechanism, involving both the soil mass and the slope. Conversely, when the footing is far from the edge of the slope (\(\lambda =4\)) (Fig. 8b, d, f, g, h), a slope is not affected and a more developed failure takes place below the footing in the form of punching shear failure with potential passive zones scarcely developed. The same failure mode is observed when the seismic coefficient increases (\({k}_{h}\) = 0.2 and \({k}_{h}\) = 0.3) (Fig. 8g, h) in comparison to Fig. 8 f corresponding to lower bearing capacity values, as expected, with the increase of kh.

In fact, the same failure mechanism takes place in Fig. 8 b, d, f, g, and h, but with a different influence area corresponding to different bearing capacity values in function of kh and \(\phi\). Bearing capacity load significantly increases with an increase in the friction angle \(\phi\) (as mentioned above, equal to 300, 600, and 1600 kPa for friction angles \(\phi\) range from 30°, 35°, and 40°, respectively, as shown in Fig. 8b, d, and f); thus, the influence area of the foundation in Fig. 8 f is much greater than that in Fig. 8 b and d, since the maximum bearing load is several times higher. The comparison of cases shown in Fig. 8 f, g, and h correspond to the same geometry, but different seismic action (kh = 0.1, 0.3, 0.4) that have an influence on the maximum bearing load.

However, since the load achieved is high enough (1600, 1480, and 1200 kPa), the influence area of the foundation is still larger than cases shown in Fig. 8 b and d.

Such behavior is not observed in Fig. 8 a, c, and e. In those cases, the location of the foundation close to the slope edge strongly conditions the bearing capacity (or alternatively, \({\eta }_{se}\)) and the global slope performance, as will be seen in the following sections. As a result, plastic shear strains are larger in the case shown in Fig. 8 a, even though the load achieved is lower than that in Fig. 8 c and e corresponding to lower \(\phi\). However, in relative terms with the maximum bearing capacity of the foundation (i.e., \({\eta }_{se}\)), the load reached in Fig. 8 a is much larger, so it develops greater strains corresponding to \({\eta }_{se}\) of about 0.6 in Fig. 8 a, while \({\eta }_{se}\) is about 0.5 for Fig. 8 c and 0.25 for Fig. 8 e. Therefore, the higher this relative load, the higher the plastic strain and the influence area of the foundation (this is also seen in Fig. 8f, g, and h where \({\eta }_{se}\) is 1.0, 0.9, and 0.75, respectively).

4 Discussion

4.1 Influence of Slope-Footing Distance and the Seismic Action

As expected, given a value for coefficient \({k}_{h}\) and ratio \(H/B\), the higher the normalized slope-footing distance \(\lambda\), the higher the value of the seismic slope coefficient \({\eta }_{se}\). Thus, footings placed next to the slope crest significantly affect the stability of the slope, conditioning its maximum load bearing capacity, as previously stated by other authors (Sawada et al. 1994; Salih Keskin and Laman 2013).

Nearly all studied cases lead to \({\eta }_{se}\) equal to or very close to 1.0 when the footing is far from the slope crest, i.e., \(\lambda\) = 4, especially for \({k}_{h}\) < 0.3 (e.g., Figs. 5a, b, e, f, i, j; 6a, b, e, f, i, j; 7a, b) indicating no reduction in the seismic bearing capacity. Thus, when \({k}_{h}\)= 0.2, many cases where the slope angle is not very steep (\(FS\) = 1.1) result in \({\eta }_{se}\) around 1.0 for \(\lambda\) = 4 (e.g., Figs. 5b, 6b, and 7b). For \({k}_{h}\) = 0.3, \({\eta }_{se}\) is in general close to 1.0 for gentle slopes (\(FS\) = 1.6 and 2.0) for \(\lambda\) = 4 as shown in Figs. 5 c, g and k; 6 c and g; and 7 c. Steeper slopes (\(FS\) = 1.1 and 1.35), either achieve a poor performance (low values of \({\eta }_{se}\)) or directly are unstable (\({\eta }_{se}\) = 0) for previously described cases. These results are also in accordance with what was obtained by LEM, as presented in Figs. 3 and 4; i.e., slopes with seismic safety factor lower than 1.0 are unstable, \({\eta }_{se}\) = 0 meaning instability of the slope-footing system. A similar behavior is observed for \({k}_{h}\) = 0.4, although in this case only very gentle slopes (\(FS\) = 2.0) result in \({\eta }_{se}\) around 1.0 (e.g., Figs. 5d; 6d, 6 h, 6 l, 6p; and 7d). Most notable exception to those tendencies is seen for \(\phi\) = 40° and \(H/B\) ≥ 3, where \({\eta }_{se}\) is far from 1.0 for \({k}_{h}\) < 0.3 (Fig. 7i, j, m, and n). However, one should take into account that maximum footing load bearing capacity (\({q}_{ult}\)) for \(\phi\) = 40° is very high when compared to the corresponding values for lower friction angles (\({q}_{ult}\) for \(\phi\) = 40° is more than 5 times such value for \(\phi\) = 30° and about 2.5 times more than it for \(\phi\) = 35°). So, an 80% of the maximum footing load bearing capacity may be considered a very high value. All in all, results indicate that a slope-footing distance of 4B (\(\lambda\) = 4) or higher has a small influence in the footing bearing capacity.

Charts show that a footing can be placed at the slope edge, for \({k}_{h}\) ≤ 0.2 and gentle slopes (\(FS\) = 1.6 and 2.0), as \({\eta }_{se}\) yield values in the range of 0.4 to 0.9 for such cases (e.g., Figs. 5a, b, e, f, i, j; 6a, b, e, f, i, j; 7a, b). Again, some discrepancies are observed for \(\phi\) = 40°, where \({\eta }_{se}\) values are below the mentioned range unless \(H/B\) ≤ 2 (Fig. 7i, j, m, and n). So, these results also point out that when very low seismic action exists (\({k}_{h}\) < 0.1), footings can be placed at the slope edge resulting in a reduction of around 50% of \({q}_{ult}\). However, for great values of \({k}_{h}\), the foundation load is significantly reduced. An inspection of charts makes one to conclude that for \({k}_{h}\) = 0.4, independently of the slope angle, as expected, footings should not be placed at the slope edge.

For values of \(\lambda\) between 0 and 4, the tendency is, as stated above, inverse with \({\eta }_{se}\). Although a very small influence of \(\lambda\) is seen on \({\eta }_{se}\) for \(\lambda\) ≤ 2 when \({k}_{h}\) ≤ 0.2 and \(H/B\) ≤ 2 (e.g., Figs. 5a, b, e, 6a), but in general,\({\eta }_{se}\) shows a clear increment when \(\lambda\) moves from 0 to 4 (e.g., Figs. 5i, m; 6i, m; 7a, e, f, i, m). This behavior also depends on the friction angle \(\phi\). For instance, when \(\phi\) = 30°, \({\eta }_{se}\) appears to reach \({\eta }_{se}\) = 1.0 around \(\lambda\) = 2 for gentle slopes (\(FS\) = 1.6 and 2.0) and \(\lambda\) = 3 for steep ones (\(FS\) = 1.1 and 1.35) as shown in Fig. 5 f and j; while if \(\phi\) = 40°, \({\eta }_{se}\) gradually increases from its minimum value (\(\lambda\) = 0) to its maximum one (\(\lambda\) = 4), as shown in Fig. 7 b and f, except for very gentle slopes (\(FS\) = 2.0) and \({k}_{h}\) ≤ 0.2, where \({\eta }_{se}\) = 1.0 is reached for \(\lambda\) ≥ 3 (e.g., Fig. 7e, i, and m). For \(\phi\) = 35°, an intermediary behavior is seen, sometimes showing \({\eta }_{se}\) = 1.0 for \(\lambda\) ≥ 3 (e.g., Fig. 6b, c, and f).

Here it should be noted again the large difference in terms of \({q}_{ult}\) between \(\phi\) = 40° and the other friction angles; i.e., 40% of \({q}_{ult}\) for \(\phi\) = 40° is a value larger than that reached at 100% for lower friction angles. So, apparently, seismic action affects much greater the performance of a footing on high friction angle soil, but this should be understood in relative figures, given that \({\eta }_{se}\) represents a % of the bearing capacity (e.g., comparison of Figs. 5a and 7a).

All in all, the increasing seismic action (higher values of \({k}_{h}\)) makes values of \({\eta }_{se}\) significantly decrease. This is apparently the parameter which most influences \({\eta }_{se}\) along with \(\lambda\). Only when both \(\lambda\) and \(H/B\) are low (e.g., \(\lambda\) ≥ 3 and \(H/B\) < 2) \({\eta }_{se}\) values are equal or close to 1.00 for gentle slopes (\(FS\) = 1.6 and 2.0) for every \({k}_{h}\), unless, as mentioned above, the slope is unstable due to the seismic action. Thus, when \({k}_{h}\) > 0.3, steeper slopes (\(FS\) = 1.1) show to be unstable, except when \(H/B\) is low and \(\phi\) = 35° or 40°.

Results are in accordance with literature (Lai et al. 2022; Sawada et al. 1994; Salih Keskin and Laman 2013) as the seismic bearing capacity of a footing close to a slope increases with the distance to the slope and decreases as the seismic factor increases.

4.2 Influence of the Slope Height and the Slope Angle

As it is well known, the higher the height of a slope, the lower its factor of safety, as previously stated by other authors (Salih Keskin and Laman 2013). Here, the results presented as normalized slope height \(H/B\) shows a similar influence. In general terms, the greater the value of \(H/B\), the greater the influence of the seismic action on \({\eta }_{se}\), decreasing its value. However, the influence of \(H/B\) gets a higher relevance when \(\lambda\) importance decreases (\(\lambda\) ≥ 3 as seen in the previous section). For instance, given \(\phi\) = 35°, \({k}_{h}\) = 0.2, \(FS\) = 1.35, and \(\lambda\) = 2, the decrease in the value of \({\eta }_{se}\) is about 30% when \(H/B\) increases from 2 (Fig. 6j) to 4 (Fig. 6n), while for both \(H/B\) = 2 (Fig. 6j) and \(H/B\) = 4 (Fig. 6n), \({\eta }_{se}\) changes around 60% when \(\lambda\) varies from 1 to 2. Thus, \(\lambda\) seems to have a greater effect in \({\eta }_{se}\) than \(H/B\). If \(\phi\) = 40°, similar results are obtained, so friction angle appears to have a little relationship here.

Regarding the influence of the slope angle, results show that higher values of the static safety factor \(FS\), while other parameters remain constant, give rise to a significant increase in coefficient \({\eta }_{se}\). This has been analyzed in sections above. Besides, the influence of the slope angle on \({\eta }_{se}\) also depends on the friction angle, i.e., the bearing capacity of the soil itself. For instance, given \(\phi\) = 35°, \({k}_{h}\) = 0.2, \(H/B\) = 2, and \(\lambda\) = 2 (Fig. 6f), \({\eta }_{se}\) increases from 0.3, 0.7, 0.9, and 1.0 for \(FS\) = 1.1, 1.35, 1.6, and 2.0, respectively. However, for the same case but when \(\phi\) = 40º (Fig. 7n), \({\eta }_{se}\) increases from 0.4, 0.5, 0.6, and 0.7 approximately for \(FS\) = 1.1, 1.35, 1.6, and 2.0, respectively. So, even though the slope angle strongly conditions the maximum bearing capacity by a footing located close to a slope edge under a seismic action, the effect is lower for higher friction angle of the ground.

Results are in accordance with literature (Mase et al. 2023; Lai et al. 2022; Salih Keskin and Laman 2013) as the seismic bearing capacity of a footing close to a slope decreases with the increase in both the slope height and the slope angle, while it increases as the friction angle increases.

4.3 Influence of the Apparent Cohesion

As specified in Sect. 2, a cohesion value equal to 1 kN/m2 is included in all simulations to avoid numerical problems, being that a common practice in numerical analysis for geotechnical purposes. That means that the term \(c{N}_{c}\) is introduced in Eq. 3, thus slightly increasing the value of \({q}_{ult}\). Figure 9 shows the comparison of the coefficient \({\eta }_{se}\) computed by the FE simulations and the one obtained if the term \(c{N}_{c}\) was subtracted both from the maximum load and the one obtained running the FE simulations (note \(c{N}_{c}\) is equal to 30, 46, and 75 kN/m2, for a friction angle \(\phi\) equal to 30°, 35°, and 40°, respectively).

Fig. 9
figure 9

Influence of the apparent cohesion (1 kPa) in the results

Full size image

As can be observed, in all the cases analyzed, the influence of the apparent cohesion makes values of \({\eta }_{se}\) with and without considering the cohesion terms match each other in more than 90%. This difference even reaches more than 95% for higher values of \(\phi\) = 40° as well as in many cases for \(\phi\) = 30° and \(\phi\) = 35°. Therefore, results obtained in the numerical simulations can be considered suitable and representative of a pure granular cohesionless soil; i.e., the influence of the apparent cohesion assumed in the analysis is negligible.

4.4 Surficial Footings Close to Slopes Without Seismic Action

The existence of a slope close to a surficial footing may be taken into account by means of correction factors (\({t}_{c}\) and \({t}_{\gamma }\)) applied to the bearing capacity factors. Thus, Eq. 3 is written as:

$${q}_{ult}=c{N}_{c}{t}_{c}+\frac{1}{2}\gamma B{N}_{\gamma }{t}_{\gamma }$$
(7)

As the term \(c\cdot {N}_{c}\) is neglected in this work, as justified in previous Sect. 4.3, Eq. 7 may consider only the second term of the expression, and compare it to Eq. 4, by that way being correction factor \({t}_{\gamma }\) equivalent to coefficient \({\eta }_{se}\), without considering the seismic action (note that the final load bearing capacity is obtained by multiplying \({q}_{ult}\) by either of such factors). Several authors proposed a definition for \({t}_{\gamma }\) based on the slope angle. For instance, Vesic (Vesic 1973) suggests using:

$${t}_{\gamma }={\left(1-{\text{tan}}\beta \right)}^{2}$$
(8)

while Brinch Hansen (Brinch Hansen 1970) indicates:

$${t}_{\gamma }={\left(1-0.5{\text{tan}}\beta \right)}^{5}$$
(9)

Those definitions are simple and very easy to apply, but they do not introduce the footing distance from the slope crest \((\lambda )\). If factor \({t}_{\gamma }\) is computed for slope angles of 16°, 20°, 27°, 32°, and 37° (slope angles used in different performed FE simulations), obtained values are 0.54, 0.40, 0.24, 0.14, and 0.07, respectively, for Vesic (Vesic 1973) proposal; Brinch Hansen (Brinch Hansen 1970) proposal yields similar values. So, this approach may underestimate the bearing capacity of footings for large \(\lambda\) values as demonstrated by FE models.

Alternatively, Meyerhof (Meyerhof 1957) proposed a chart which provided the value of the bearing capacity factor \({N}_{\gamma q}\) for a footing close to a slope on granular soil. Neglecting the term \(c{N}_{c}\) leads the ratio between \({N}_{\gamma }\) factor determined with and without the influence of the slope proximity to being equivalent to coefficient \({\eta }_{se}\), without considering the seismic action. For Meyerhof (Meyerhof 1957), \({N}_{\gamma q}\) depends on both the slope-footing distance \(\lambda\), the slope angle \(\beta\), and the soil friction angle \(\phi\). Only values for (i) \(\phi\) = 30° and \(\beta\) = 30° (\(F\) = 1.0), (ii) \(\phi\) = 40° and \(\beta\) = 20° (\(F\) = 2.0), and (iii) \(\phi\) = 40° and \(\beta\) = 40° (\(F\) = 1.0) are provided in the chart, being the rest of values interpolated. For a surficial footing placed at the slope crest \((\lambda\) = 0), the mentioned ratio approximately yields 0.13, 0.34, and 0.04 for cases (i), (ii), and (iii), respectively. If \(\lambda\) = 1, the ratio approximately yields 0.65, 0.60, and 0.35, respectively. If \(\lambda\) = 2, the ratio approximately yields 1.00, 0.75, and 0.65, respectively. If \(\lambda\) =3, the ratio approximately yields 1.00, 0.80, and 0.75, respectively. And, if \(\lambda\) = 4, the ratio yields 1.00 for all cases. Thus, ratios with and without considering the influence of the slope proximity obtained by Meyerhof (Meyerhof 1957) proposal for \(\lambda\) = 0 are similar to values obtained by Eqs. 8 and 9.

When the previously determined values of \({N}_{\gamma q}\) are compared to \({\eta }_{se}\) values obtained in this work by FE model, classical proposals tend to underestimate the bearing capacity of a foundation close to a slope crest. As previously said, \({\eta }_{se}\) yield values in the range of 0.4 to 0.9 for low seismic coefficient (\({k}_{h}\) = 0.1), so for non-seismic action, at least 0.5 should be considered for \({\eta }_{se}\), sometimes being even greater.

For \(\lambda\) ≥ 1 and \({k}_{h}\) = 0.1, \({\eta }_{se}\) tends to achieve values similar or slightly inferior to the ones given by Meyerhof (Meyerhof 1957) for the corresponding \(\lambda\) parameter, especially when \(H/B\) ≤ 2, while Eqs. 8 and 9 clearly underestimate them. Meyerhof’s (Meyerhof 1957) chart also confirms the general threshold \(\lambda\) ≥ 4 for considering that the slope-footing distance has no influence on the footing bearing capacity. Besides, such threshold also follows the work of Castelli and Lentini (Castelli and Lentini 2012) who set it in \(\lambda\) ≥ 2.5 for \(\phi\) = 30° and \(\lambda\) ≥ 3.5 for \(\phi\) = 40°. An inspection of values of \({\eta }_{se}\) for \({k}_{h}\) = 0.1 shows that those thresholds approximately match the results obtained in this work.

5 Example of Application of the Charts Developed

The charts showed in Figs. 5, 6, and 7 may be used by practitioners to estimate the bearing capacity of a surficial strip foundation next to a slope in a seismic area. To illustrate the use of the charts developed, an example is given.

The foundation to be designed consists of a strip footing of 3.0 m width (\(B\)) located at 3.0 m of the edge of a slope of 9.0 m of height (\(H\)) with an inclination 3H:1 V. The ground is a granular soil, with null cohesion, friction angle \(\phi\) = 35°, and unit weight \(\gamma\) = 18 kN/m3. Horizontal seismic coefficient \({k}_{h}\) is assumed as 0.1, with ratio \({k}_{v}/{k}_{h}\) = 0.5. From this data, the bearing capacity of the foundation located at the ground surface without considering the seismic action and the slope may be obtained using Eq. 3. For computing the bearing capacity factor \({N}_{\gamma }\), Eq. 2 is used. This yields a bearing capacity \({q}_{ult}\) equal to 915.84 kN.

For considering the seismic action and the slope existence, one uses the developed charts. Since \(\phi\) = 35°, ratio \(H/B\) = 3, and \({k}_{h}\) = 0.1, the chart to use corresponds to Fig. 6 e. Inclination of the slope 3H:1 V means approximately a slope angle \(\beta\) = 27°, so the simplified static safety factor will be \(FS\) = tan \(\phi\) / tan \(\beta\) = tan \(35\) / tan \(27\) = 1.37. Parameter \(\lambda\) will result in \(\lambda\) = 1, since the distance from the footing to the slope is equal to the footing width. Using the aforementioned chart for \(\lambda\) = 1 and \(FS\) = 1.37, the chart indicates \({\eta }_{se}\) ≈ 0.63. So, bearing capacity considering both the slope existence and the seismic action will be \({q}_{ult,se}\) = 915.84·0.63 ≈ 577 kN. Figure 10 shows the procedure followed.

Fig. 10
figure 10

Example of the application of the charts developed

Full size image

6 Conclusions

The design of surficial strip footing at ultimate limit state requires checking its bearing capacity. Analytical solutions are commonly used to address the problem for the static case and a plain ground. However, the seismic action and the proximity of a slope reduce the bearing capacity. Until now, there is no clear analytical expression or procedure to use for the design of a surficial strip footing in such cases. In this work, the FEM was used to conduct a thorough parametric study involving 960 models to study the seismic bearing capacity of a surficial strip footing on a frictional soil close to a sloping ground. Input parameters considered included the soil strength (friction angle \(\phi\)), slope height (\(H\)), slope angle (measured in terms of the static safety factor), seismic acceleration (defined by the horizontal pseudo-static seismic coefficient \({k}_{h}\), and assumed relation between vertical and horizontal pseudo-static seismic coefficient \({k}_{v}\) = 0.5 \({k}_{h}\)), foundation size (strip footing of width B), and distance to the slope (measured in terms of the footing width). A cohesion value of 1 kPa was assumed to avoid numerical problems. This cohesion value has been demonstrated to be negligible in the results. Additionally, 192 limit equilibrium models were performed to complement the work and analyze how the seismic action may influence the safety of slopes without any load at the top.

As FE models involved a large number of geotechnical and geometrical parameters, results are given as design charts that provide the seismic slope coefficient \({\eta }_{se}\) (Figs. 5, 6, and 7). This coefficient is a global reduction factor of the foundation bearing capacity depending on the horizontal pseudo-static seismic coefficient \({k}_{h}\), the static safety factor, the slope height/footing width ratio (\(H/B\)), and the distance to the slope. From the work developed and the analyses conducted, the following conclusion can be drawn:

  • The slope-footing distance together with the horizontal pseudo-static seismic coefficient \({k}_{h}\), i.e., the seismic action, are the parameters which most influences the bearing capacity of a surficial strip footing on frictional soils. The proximity of the slope also influences its failure mechanism. When the foundation is very close to the slope edge, the failure includes both the soil mass and the slope. For a slope-footing distance of 4B or higher, the slope has a small influence in the foundation bearing capacity, with a developed punching failure taking place below the footing.

  • Locating shallow foundations on frictional soils close to a slope (i.e., slope-footing distance lower than 4B) when \({k}_{h}\) ≥ 0.2 is not recommended unless gentle slopes are planned (static safety factor equal or greater than 1.6). For \({k}_{h}\) = 0.4, only when \(\phi\) = 40° and the static safety factor of the slope is equal or greater than 2.0, the bearing capacity of a foundation is expected not to be low. Besides, the seismic bearing capacity clearly decreases when slope-footing distance is reduced. If the foundation is placed at the slope edge (null slope-footing distance), for \({k}_{h}\) ≤ 0.2 and gentle slopes, the bearing capacity is about 65% (values range between 40 and 90%) the one corresponding for a static, plain ground case. If \({k}_{h}\) > 0.3, surficial strip footings on frictional soils should not be placed at the slope edge (even for gentle slopes).

  • The greater the ratio \(H/B\), the greater the negative influence of the seismic action on the bearing capacity. A ratio \(H/B\) > 4 has little influence on the bearing capacity of foundations and the dynamic slope behavior. In such cases, chart values for \(H/B\) = 4 can be used. Low values of \(H/B\) may mitigate the effect of both the seismic action and the proximity to the slope in the foundation bearing capacity, but from a ratio \(H/B\) ≥ 3 and \({k}_{h}\) ≥ 0.3, many slopes tend to be unstable. Besides, ratio \(H/B\) has a higher relevance in reducing the seismic bearing capacity when slope-footing distance is equal or greater than 3B.

  • Gentle slope angles (i.e., static safety factor equal or greater than 1.6) tend to have low influence on the seismic bearing capacity. However, this effect is lower for higher friction angles of the ground.

  • When compared to the classical proposal for designing shallow foundations close to slopes without the seismic action, results obtained in FE models show that these analytical solutions clearly underestimate the bearing capacity.

  • The charts developed in this work (Figs. 5, 6, and 7) are a useful tool for the estimation of the influence of different parameters on the bearing capacity of a surficial strip footing considering the seismic action and a slope. Likewise, those charts can be used by practitioners in the first step of the designing process.