Design Charts for Geogrid-Reinforced Granular Working Platform for Heavy Tracked Plants over Clay Subgrade

Abstract

This study investigates the bearing capacity of a geogrid-reinforced granular working platform for heavy tracked plants on clay subgrade using a 2D plane strain finite element method. It substantially extends a case study investigated by incorporating wider soil parameters, depth-to-width ratios and geogrid stiffness modulus. The developed models are first verified by comparing them with the published literature and found to be in good agreement. The parametric modelling results are then used to develop a comprehensive set of design charts with non-dimensional parameters, bearing capacity ratio verses shear strength ratio, so that they can be directly used by practitioners. With the help of a design example, minimum design thickness of the granular working platform is compared and benchmarked with other established design methods. The results show that the proposed design charts and methods are comparable and provide reasonable predictions for the bearing capacity and working platform design thicknesses. A design example shows that thickness of the geogrid-reinforced granular base could be reduced from 1.2 to 55.6% for different geogrid strengths whereas the reduction is very nominal for soft geogrids ranging from only 1.2 to 3.0%.

Introduction

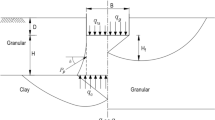
Working platforms are temporary geotechnical structures that provide a stable support during operations to prevent failure and overturning. The supporting ground below the track needs to be stable with adequate bearing capacity to withstand the pressure of the track to prevent failure. Due to the varying nature of soil and complex interaction between the layers, various considerations and simplified assumptions have been used to formulate a particular design method (MIDAS 2017). The purpose of the granular layer above weak subgrade is to provide an all-weather operating surface with a minimum bearing capacity without subgrade failure through excessive deformation. This means that the granular fill needs to be sufficiently thick to dissipate the vertical stresses induced by the applied pressure to a level not exceeding the subgrade shear strength. In order to further improve the bearing capacity, a common ground improvement technique is to place a layer of geosynthetics, particularly geogrid, at the interface between granular fill and soft subgrade as a separation layer both to improve its load carrying capacity and to limit excessive settlement. Therefore, it is feasible to convert the tracked plant bearing capacity problem to that of the traditional bearing capacity problem for surface strip footings on layered soils with a relatively thin top dense granular base layer overlying the semi-infinite depth weak soil subgrade, as shown in Fig. 1.

Fig. 1

Schematic diagram and terminologies of the problem

Failure to comprehend the unpredictable nature of soil and improper working platform design has resulted in a number of track plants toppling over while operating on granular working platforms. Overturning may result in severe injuries and fatalities, delays to the work, potential prosecution, uninsured costs, increased insurance premiums, damage to reputation and loss of business. McCann et al. (2009) reported that 323 fatalities in 307 crane incidents occurred in the USA between 1992 and 2006 and a total of 68 fatalities (21%) which were associated with the collapsed of a crane. In the 10 years from 2004 to 2013, 22 of the total 359 workers died in the Australian construction industry involved the use of a crane (Gharaie et al. 2015). ARTC (2020) reported that between 2003 and 2015, 47 workers were killed in incidents involving cranes.

The conventional bearing capacity calculations (Terzaghi 1943; Meyerhof 1963; Hansen 1970; Vesic 1975; Bowles 1996) in which bearing capacity factors are adopted are mostly for homogeneous soil and isotropic conditions for simplification. The bearing capacity of footings on layered soil is dependent on the properties of the bottom layer, unless the thickness of the topsoil layer is sufficiently large enough to accommodate the entire failure mechanism. The layered soil system can be a strong upper layer and weak lower layer or vice versa. For this study, the upper layer is strong and the lower layer is weak as it resembles dense granular fill over soft clay subgrade for a working platform.

The behaviour of geogrid-reinforced granular working platforms under static tracked plant pressure is analysed using a 2D plane strain finite element method in ABAQUS software. The finite element model (FEM) takes into consideration the applied load, geogrid properties, soil properties and geometric parameters in the analysis. FEM is well suited to investigate such a complex geotechnical engineering problem and the bearing capacity of footings over a two-layered soil system as an experimental approach is time consuming and expensive, and commonly used classical solutions such as limit equilibrium are no longer applicable (Mosadegh and Nikraz 2015). The developed FEM model is first verified using published research data and benchmarked against other methods. Once the verification is complete, the case study purposed by Chua et al. (2021) is extended incorporating wider soil parameters (granular platform friction angle (ϕ = 35 to 45°), clay subgrade cohesion (c_u = 15 to 150 kPa), depth-to-width ratios (H/B = 0.5 to 2.0), and geogrid stiffness modulus, E (weak = 35 MPa, medium = 1970 MPa and stiff = 4730 MPa)) to generate a comprehensive set of dimensionless design charts: bearing capacity ratio (q/γB) vs shear strength ratio (c_u/γB). These design charts are ready to be used by practitioners for the conditions within these wide ranges.

Literature Review

There have been several attempts to estimate and model bearing capacities and settlements of both homogeneous and layered soils over several decades. These attempts have produced a substantial corpus of work covering analytical methods, empirical methods, experimental observations and numerical simulations. The approaches used in the past can be broadly divided into three general categories: limit equilibrium, limit analysis and slip-line methods (Cheng et al. 2016). In limit equilibrium methods for assessing failure in soil, a simple induced failure surface shape of a planar or circular is assumed and is widely used owning to its simplicity and reasonably good predictions. Two commonly used limit equilibrium methods are the semi-empirical methods proposed by Meyerhof (1974) and Hanna and Meyerhof (1980), and the project area method proposed by Yamaguchi (1963). The former method assumes a punching shear failure mechanism with a shearing resistance along the side of vertical block (that is α = 0°). They used limit equilibrium analysis to formulate the design equations by using the punching shear coefficient derived from laboratory model tests at 1 g and presented in charts. These charts were not in non-dimensional form and are only appropriate for the granular layer unit weight and thickness used in this study (Burd and Frydman, 1997). The derived equation for the dense granular layer on soft clay subgrade is expressed in Eq. (1).

$$q_u=c_uN_c+\gamma H^2\left(1+\frac{2D}H\right)K_s\frac{\tan\phi}B\gamma D\leq q_g$$

(1)

Equation (1) assumes dense granular layer on soft clay. As the strength of clay subgrade increases relative to the granular layer, this method is shown to overestimate the ultimate bearing capacity (Shiau et al. 2003). It is worth noting that when q_u/q_g equals unity, the bearing capacity is equal to the granular layer alone and a critical depth ratio is reached at which the clay subgrade has no effect on the bearing capacity. The finite element limit analysis shows a similar result in BR470 (BRE 2004) and over-predicts ultimate bearing capacities for sites with very soft clay subgrade (Eshkevari and Abbo 2014). By considering the surcharge transfer in the granular layer that could extend up to 5B, the bearing capacity may be enhanced by 20–30% and force critical failure surface to be deeper (Madhav and Sharma 1991; Lees 2017).

In the projected area (or load spread) method, the granular layer is assumed to dissipate the load uniformly to the underlying clay subgrade at a constant angle α to the vertical direction without accounting for the shear strength contribution of the granular layer, as in Eq. (2) (Terzaghi et al. 1996; Yamaguchi 1963).

$${q}_{u} = \left(1+\frac{2H}{B}\mathrm{tan}\alpha \right)\left({c}_{u}{N}_{c}+ {p}_{0}^{\mathrm{^{\prime}}}\right)- \frac{W}{B+2H\mathrm{tan}\alpha }$$

(2)

N_c used in Eqs. (1) and (2) is calculated for one rupture figure (failure zone) and the simple superposition of other factors implies that the bearing capacity for the layered soil system is an approximation.

Many load spread angles have been recommended by various authors; 18.4° by Young and Focht (1981); 45° by Myslivec and Kysela (1978); equal to ϕ by Baglioni et al. (1982) and Das and Dallo (1984); 26.6° by Terzaghi and Peck (1948), Kraft Jr and Helfrich (1983), Dutt and Ingram (1984), Chiba et al. (1986) and Tomlinson (1986); 18.4–11.3° by Kellezi and Kudsk (2009); and around 40° for geotextile and greater than 45° for geogrid reinforcement by Palmeira and Antunes (2010). A load spread method assumes that the vertical stress distribution for the two-layer soil system is similar to that of elastic solid estimated by Boussinesq analysis for small deformation and homogeneous material. The arbitrary assumption of positive dispersion angle α and the neglected shear resistance of granular layer is questioned as load spread angle α changes as strains increase towards failure and may result in an unreliable prediction. The value of α is dependent on shear strengths of the soils, stiffness ratio between the layers and the geometry, H/B (Kraft Jr and Helfrich, 1983, Kenny and Andrawes 1997; Ballard et al. 2010; Lees 2017, 2020). Eshkevari (2018) used the limit equilibrium method to develop a new model and found the dispersion angle α can be negative or zero. It shows that there is no consensus in the selection of load spread angle α despite that it has significant influence on the estimation of bearing capacity.

The limit analysis method is used to estimate the upper and lower bounds of the ultimate collapse load without considering the eventual deformations by progressive refinement until the exact solution can be approached (Aysen 2002). In slip-line analysis, a set of differential equations of plastic equilibrium is established at yield and equilibrium conditions accompanied with initial soil stress conditions (Chen 1975). By using the equations of statics and solving the differential equations, the exact solution is determined (Grahnström and Jansson 2016). Slip-line analysis is more complex and is not widely used by practitioners.

Industry Practices in Working Platform Design Methods

Historically, the approach to design the granular working platforms for tracked plant has not been undertaken in a consistent manner across the industry. There are no unified standards or criteria prescribed by the approving authorities. Generally, for small projects, it is based on empirical or past experience of suitable material and thickness. However, for large projects, more formal design methods based on the classical bearing capacity methods for shallow foundations are being used for tracked plant working platforms. These methods are not entirely appropriate considering the differences between building foundations and the tracked plants in terms of load duration, allowable differential settlement, the significance of the project, etc. The building industry is moving away from empirical method in favour of analytical method (BRE 2004). The common working platform design methods used in the building industry are summarised in Table 1.

Table 1 Industry practices in working platform design methods

Finite Element Models

Numerical analysis is an alternative method for predicting bearing capacity of shallow foundations on two-layer soil as demonstrated in previous studies (Burd and Frydman, 1997; Zhu 2004; Helwany 2007; Ballard et al. 2010). Numerical techniques can deal with complicated loadings, geometry of complex shape, anisotropy, layered soils and complex stress–strain relationships. It is also convenient with the added advantage of combining all the parameters into a single problem, less time consuming to set up than experimental models and when commonly used classical solutions such as limit equilibrium are no longer applicable.

There are many studies on bearing capacity of strip footings with 2D plane strain model by FEM methods conducted over the last four decades. However, most of these studies are not limited to footings on the surface of the soil and mostly related to reinforced soil foundation rather than working platforms. Hence, this paper applies FEM to estimate the bearing capacity of strip footings on the surface of the existing soil and develops a comprehensive set of design charts for working platforms for heavy tracked plants.

FEM for Working Platform: Model and Material Properties

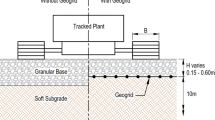
The tracked plant footprint on a working platform has a long length dimension compared to its width like a strip footing and can be analysed assuming 2D plane strain conditions. The granular working platform model dimensions used in the FEM are 10.3 m wide by 150 to 600 mm deep above 10-m-thick clay, as illustrated in Fig. 2(a). The geogrid reinforcement is placed at the interface of clay subgrade and granular layer. The outer model boundaries are chosen to ensure the effects of load dissipated are contained within the model and the stresses at the outer boundaries are less than 0.01% of the applied contact pressure (Abu-Farsakh et al. 2008). Considering the tracked plant elevation view is symmetrical, only one of the tracks is modelled. For the boundary conditions, the vertical sides are fixed in a horizontal direction with vertical displacement, and the bottom of the model is fixed in both vertical and horizontal directions as shown in Fig. 2(b). The track is represented by a weightless rigid body with vertical load applied as uniform pressure over the track footprint. Depending on the test conditions, a displacement method is applied to the footing width (B) equal to 300 mm, as shown in Fig. 2(a).

Fig. 2

Plane strain model geometry and boundary conditions with strip loading

An eight-node biquadratic plane strain quadrilateral shape function and a reduced integration (CPE8R) element type were selected to discretise the subgrade and granular base, while a two-node linear displacement 2D displacement truss element type (T2D2) was used to discretise the geogrid reinforcement. The top granular layer was assumed to be stronger than the bottom clay layer. The mesh topology relating to optimum element mesh size and density including finite element model verification are detailed in Chua et al. (2021). Mohr–Coulomb plasticity models are selected to represent the nonlinear plastic behaviour of the granular base and clay subgrade, where the shear strength developed in soil is a function of internal friction, cohesion and applied stress. The soils are simulated as weightless materials because in situ stress has no effect on elastic settlement (Griffiths 1982).

The interaction simulation for geogrid and soil interface consists of two components. One is hard contact for the normal direction to the interface with no separation allowed between the two interfaces (geogrid-granular and geogrid-clay). Two is in the tangential direction, and a penalty method with a Coulomb friction model is used to simulate the frictional constraints to allow an elastic slip of 0.001 m when the finite value of the interface shear stress is reached (Perkins and Cuelho 1999). The friction model is represented by using geogrid and soil interface friction coefficient and elastic slip input data. This is done using kinematic coupling constraints to constrain the movement of a granular and clay surface to the geogrid movement and ensure that the geogrid stays in place (SIMULIA 2013).

The modulus of the granular base is dependent on the material characteristics, the stress level it operates and the stiffness of the underlying in situ subgrade. Therefore, the modulus of the granular base is influenced by the modulus of the subgrade (Austroads 2018). For design subgrade CBR of 3% or more, modulus stress dependency in the sub-layering rules is applied to address the effect of the underlying support. In the case of subgrade CBR less than 3%, the subgrade materials are unlikely to behave elastically when loaded. Under this scenario, the modulus ratio of the granular base to subgrade soil is usually taken to be 1.0 to 5.0 as recommended by Heukelom and Klomp (1962) and a ratio of 2.0 to 5.0 was selected for the FEM analysis.

The subgrade soil is assumed to behave in an undrained condition and its shear strength is equal to its undrained cohesion c_u. In this study, the value of c_u is deduced from the CBR value of the subgrade soil with CBR less than 5% using the following relationship as suggested by Giroud and Noiray (1981).

$${c}_{u} = {f}_{c} CBR$$

(3)

where f_c = factor equal to 30 kPa. The empirical relationship (Eq. 4) as recommended in Austroads (2018) is used to deduce the stress-dependent subgrade modulus for soils with CBR 3% or more but not exceeding 15%.

$${E}_{sg }= 10 \times CBR$$

(4)

The nonlinearity behaviour in soil is attributed to dilatancy. In granular soils, dilatancy increases with increasing relative density and decreases with increasing confining stress levels. The influence of the associated flow rule is significant for higher friction angle (ϕ > 30°) up to 15% as demonstrated in Loukidis and Salgado (2009). The failure mechanism is deeper and wider when the dilation angle is higher (Potts et al. 2001; Mosadegh and Nikraz 2015). Therefore, numerical analysis is performed assuming associated flow. The selection of dilatancy angle ψ is based on the approximation used in Plaxis analysis and studies by Shiau et al. (2003) and Ameratunga et al. (2016).

$$\psi = \phi - 30^\circ$$

(5)

where ψ = 0 for ϕ < 30°. Other presumptive material constitutive model input parameters considered in this parametric study are based on published data from Leng and Gabr (2005), BRE (2004) and Bowles (1996) as summarised in Table 2. Geogrid in the model exhibits, in general, components of elasticity, plasticity and directional dependency and creep is direction, time and temperature dependent. But this is not practical for use in the numerical simulations because it requires many input parameters which are not readily found in the product datasheets and design manuals produced by the manufacturers. It is for this reason that geogrid reinforcement is modelled as a linear elastic material. The geogrid properties are chosen to encompass the full range of geogrid available in today’s market (Erickson and Drescher 2001).

Table 2 Material properties for FEM analysis for developing working platform design charts

Table 2 shows a band of granular base modulus values 10–200 MPa being used in the modelling. The modulus of the granular base is dependent on the inherent characteristics of the materials, the stress level at which they operate, the thickness of the base layer and the modulus of the underlying subgrade layer. The ability to compact the granular base is dictated by the degree of support provided by the underlying subgrade layer. Therefore, the modulus of the base layer can be significantly lower when placed over soft subgrade. For a loose granular base overlying soft subgrade with CBR less than 3%, the lower bound of the modulus ratio of a granular base to subgrade ranging from 2 to 3 has been adopted. In the case of a dense granular base over stiff subgrade with CBR greater than 3%, the modulus ratio of 3 to 5 has been used, as used in several past studies. Heukelom and Klomp (1962) recommend using a modulus ratio of a granular base to subgrade soil between 1.0 and 5.0. Hammitt (1970) used from 1.7 to 17 with a ratio of 5.23 based on linear regression. Leng and Gabr (2002) generated a stress distribution angle versus modulus ratio chart for a two-layer system. The chart infers that the modulus ratio is between 3.0 and 6.5 for the granular base with ϕ ranging from 35 to 45°.

The granular working platforms analysed are summarised in Table 3. Based on the number of pavement configurations premutation, a total of 288 cases have been analysed in this parametric study to generate enough data to produce the design charts. For each granular working platform type, the critical compressive stress on the top of the granular layout directly underneath the applied vertical displacement is extracted from the finite element model after each numerical computation.

Table 3 Granular working platform configurations

FEM for Working Platform: Results and Discussions

Modelling of Strip Footing on Surface over Two-Layered Soils

Past researchers (Craig and Chua 1990; Michalowski and Shi 1993; Burd and Frydman 1997) have shown that the bearing capacity and the performance of shallow foundation on a granular base layer underlying a soft clay are governed by dimensionless groups as shown in Eq. (6).

$$\frac{q}{\gamma B}=f\left(\frac{H}{B} , \frac{{c}_{u}}{\gamma B} , \phi , E\right)$$

(6)

The bearing capacity ratio (q/γB) represents the average pressure under a strip footing which is a function of four groups of parameters. The work done by weight of the soft clay must be zero considering the incompressibility of the soft clay and the geometry of the failure mechanism. Therefore, the bearing capacity of the footing is independent of the unit weight of the clay. FEM is first used to compare design charts with published studies followed by a compressive set of design charts. Minimum design thicknesses using several methods are also compared and discussed.

Comparison of FEM Results with Published Studies

Sample design charts for a working platform granular base are first developed using FEM models and are compared with published results. The comparison is done for applicable cases available in the published literature for specific conditions and shown in Fig. 3(a) to Fig. 3(d).

Fig. 3

Comparison of FEM models with published studies

Design charts for an unreinforced granular base shown in Fig. 3(a)–(c) are compared with the displacement finite element method solutions of Burd and Frydman (1997), the analytical kinematic predictions of Michalowski and Shi (1993), semi-empirical results proposed by Hanna and Meyerhof (1980), the advanced upper and lower bound techniques suggested by Shiau et al. (2003), the limit equilibrium analysis proposed by Al-Shenawy and Al-Karni (2005), the FEM upper bound multi-block solutions by Huang and Qin (2009), the discontinuity layout optimisation method by Zheng et al. (2019) and the rigid-plastic finite element method by Pham and Ohtsuka (2021). For the case of an unreinforced granular base with internal friction angle (ϕ) equal to 35°, 40° and 45° and depth-to-width ratio (H/B) equal to 1.0 and 2.0, FEM modelling results closely align with the other studies. It is worth noting that most of the past studies are limited to low c_u/γB values.

The geogrid-reinforced granular base results (q/γB) are compared with results by Shahkolahi and Crase (2012) which is based on BR470 (BRE 2004) and the surcharge transfer design method (now called T-value method) by Lees and Matthias (2019). For the case of a geogrid-reinforced base with friction angle (ϕ) equal to 40° and depth-to-width ratio (H/B) equal to 1.0, Fig. 3(d) shows FEM results about the bearing capacity ratio (q/γB) at larger values of shear strength ratio (c_u/γB) which are comparable to the T-value method by Lees and Matthias (2019). For c_u/γB greater than 3, the results (q/γB) by Shahkolahi and Crase (2012) are comparatively lower. This could be attributed to the safety factor of 2 being applied to the ultimate tensile strength of the geogrid reinforcement. In addition, by assuming the mobilised friction angle of α = 2ϕ/3 regardless of granular platform, soil parameters and the relative strength of the two layers might have resulted in a conservative estimate of the actual resistance. Nonetheless, the FEM modelling results are closely comparable with these studies.

For unreinforced and geogrid-reinforced (geogrid stiffness modulus E = 1970 MPa) granular base estimates of the bearing capacity ratio (q/γB) values, the results trend towards upper bound solution. Overall, the results as indicated in Fig. 3 show that the design charts developed using FEM give a comparable bearing capacity estimate with those published previously.

Design Charts for Working Platform for Heavy Track Plants

The effects of the shear strength of the clay subgrade or the shear strength ratio (c_u/γB) on the bearing capacity ratio (q/γB), for the various values of ϕ for unreinforced and geogrid-reinforced granular base working platforms with the allowable settlement of 50 mm, are illustrated by the design charts as shown in Figs. 4, 5, 6, and 7. The results represent q/γB as a function of the dimensionless quantities H/B, c_u/γB, ϕ and E and independent of the unit weight of the clay. In each figure, separate diagrams are shown for the internal friction angle of the upper granular base layer: 35°, 40° and 45° are denoted as (a), (b) and (c) respectively. These plots are based on the average value of bearing capacity obtained from ABAQUS FEM analysis with different H/B values ranging from 0.5 to 2.0 for soil parameters summarised in Table 2. It is clear from Figs. 4(a)-(c)–7(a)-(c) that the bearing capacity ratio increases with shear strength ratio for constant H/B. In the case of H = 0 (when there is no working platform), the bearing capacity increases proportionally to the clay strength. The general pattern of these results for an unreinforced granular base is broadly aligned with past researchers (Florkiewicz 1989; Michalowski and Shi 1993; Burd and Frydman 1997).

Fig. 4

Dimensionless limit pressure on unreinforced granular base over soft clay subgrade

Fig. 5

Dimensionless limit pressure on soft geogrid-reinforced granular base over soft clay subgrade

Fig. 6

Dimensionless limit pressure on medium geogrid-reinforced granular base over soft clay subgrade

Fig. 7

Dimensionless limit pressure on stiff geogrid-reinforced granular base over soft clay subgrade

In practice, these design charts can be used to estimate the bearing capacity of a granular base working platform with track plant width B trafficked on the granular base layer thickness H with internal friction angle ϕ and the unit weight of granular base γ rest on the clay subgrade with undrained shear strength of c_u. The estimated bearing capacities from these design charts satisfy structural performance requirements and serviceability criterion of 50 mm allowable rut depth.

Comparison of Minimum Design Thicknesses of the Working Platform

The developed design charts for unreinforced and geogrid-reinforced granular working platforms are used to calculate minimum design thicknesses and are compared with existing methods (BR470 by BRE (2004), CIRIA SP123 by Jewell (1996) and Okamura et al. (1998), several load spread methods by Eshkevari (2018) and Lees (2020) with the help of a design example). The intent of this is to benchmark against these methods to determine the minimum platform thicknesses. The track plant loading conditions and soil data used in this design example are based on published data from Scotland et al. (2019) as summarised in Table 4.

Table 4 Material properties for working platform design example

The comparison of minimum platform thickness using the FEM design charts and other methods’ results is summarised in Fig. 8. It shows that the minimum platform thickness required for the loading condition varies widely depending on the method considered.

Fig. 8

Comparison of platform thicknesses (UR, unreinforced; R, geogrid-reinforced)

For unreinforced cases, BR470 (BRE 2004) shows the thickest platform thickness for c_u greater than 35 kN/m² followed by CIRIA SP123 (Jewell 1996; Okamura et al. 1998) and the load spread method (Eshkevari 2018; Lees 2020). The results show that the BR470 method is conservative in comparison to other methods resulting in uneconomic platform thicknesses. This is attributed to conservative input parameters used in the BR470 method. This finding is in good agreement with the observations by the Federation of Piling Specialists (2005) and EFFC/DFI (2019). In the case of Okamura et al. (1998), the assumed positive load spread angle α between the failure planes and vertical direction is inconsistent with the behaviour of layered soils whereby the failure planes’ inclined angle increases as the strength of the granular base relative to clay subgrade increases. In addition, the simplified assumption of using Rankine’s passive coefficient to estimate horizontal stresses in the failure plane has underestimated the mobilised resistance of the granular layer. The discrepancy in predicting α and use of Rankine’s passive coefficient in the formulation could have been attributed to the more conservative designs. Furthermore, the superposition formulas Okamura et al. (1998) used were a positive dispersion shear angle in their failure model, which may have attributed to the underestimation of the bearing capacity for the high shear strength of the clay subgrade. On the contrary, Eshkevari (2018) found that the shear angle α in the failure mode showed either a positive or negative is possible depending on the model geometry and relative strength of the two-layer soils. This may have explained Eshkevari’s (2018) method that resulted in no significant difference in minimum platform thickness for c_u greater than 35 kN/m².

The value of the load spread angle assumed in the computation has significant influence on the estimated bearing capacity and the required platform thickness. This is attributed to shear strength and load spreading of the overlying granular layer has not been accounted for resulting in the in accurate estimation of bearing capacity. It is apparent from this design example that that is not the case which explains the traditional load spread method is the thinness by comparisons with other methods and may result in unsafe prediction of bearing capacity. It shows that with the increase in load spread angle there is a decrease in the load transfer to the lower clay layer and vice versa. This result reveals that the load method gives a conservative prediction of bearing capacity.

In the case of soft geogrid reinforcement, it is not effective in reducing granular base thickness in all cases. This shows that soft geogrid reinforcements with a low tensile strength is not effective in enhancing the structural strength of the working platform. The medium and stiff geogrid reinforcement results from the design charts are comparable to CIRIA SP123 (Jewell 1996). The geogrid-reinforced platforms are thinner than unreinforced platforms in all cases except for the load spread method. This is attributed to the uplift forces generated by the geogrid reinforcement during the deformation and the mobilisation of the axial tensile forces of the geogrid reinforcement layer. The transfer of a part of the vertical load to a horizontal load carried by the reinforcement thereby prevents shear failure of the soil resulting in overall increase in bearing capacity of the reinforced layered soil system. The FEM design chart approach for the unreinforced case shows closer agreement when compared with Lees’ (2020) value method for soft subgrade conditions up to around c_u = 30 kN/m². Overall, this design example illustrates the difficulty of obtaining exact solutions for a two-layer soil system.

Table 5 shows that the reduction in the thickness of the granular base attributed to the stiff geogrid reinforcement is more than that of the medium geogrid followed by the soft geogrid for 610-, 495- and 410-mm granular base layer thicknesses. The granular base thickness reduction from a loose to dense granular base varies from 1.2 to 55.6%. This infers that irrespective of the granular base layer thickness, the stiff geogrid is more effective than soft and medium geogrids in the reduction of the granular base layer thickness. In all cases, soft geogrid reinforcement yields nominal reduction in granular base thickness ranging from 1.2 to 3.0%.

Table 5 Granular base reduction values for q/γB = 50 and c_u /γB = 5 for 50 mm surface deformation

Conclusion and Recommendation

This study uses a 2D plane strain finite element analysis technique to model a two-layer soil system reinforced at the interface and subjected to surface applied loading and to simulate the soil behaviour of unreinforced and geogrid-reinforced granular layers over the clay subgrade under tracked plant pressure. It is an extension of a previous case study by Chua et al. (2021) for wider material properties. The results of the analysis are verified with the results from published literature and shown to be comparable. The parametric results are then used to generate a comprehensive set of dimensionless design charts (q/γB vs c_u /γB) for a wide range of material parameters that go beyond the coverage in previous studies. These charts could be used by practitioners directly to evaluate the cost-effectiveness of a geogrid-reinforced granular base as compared to conventional unreinforced granular working platforms. The design charts can also be used for surface strip footings on layered soils.

The comparison of minimum platform thicknesses with existing methods also shows a relatively close agreement. A closer look at the amount of reduction in the thickness of a granular working platform for a specific case revealed that there is hardly any reduction in thickness by using soft geogrids (less than 3%) whereas the reduction in the thickness is substantial (up to 55%) for stiff geogrids. As the proposed design charts are verified by a relatively small literature database due to lack of sufficient previous studies resembling the problem investigated in this study, it would be beneficial to verify them by using field tests.