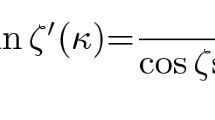Abstract
We present the conjecture that the fundamental notions of physics, including such basic concepts as spin, charge(s), mass and spacetime, emerge from a mathematical theory having to do with fluctuations in the metrics of 2-manifolds. This involves looking at a set of 2-manifolds whose metrics depend on a global parameter \(t\), where each manifold is also associated with a set of six parameters whose values change continuously along \(t\) depending on the metrics and associated parameters of all the other manifolds. More intuitively, and specifically, what we do is define objects that generate oscillations on affine planes in \(R^3\), parameterized by the global parameter \(t\), where the plane associated with each object changes continuously along \(t\) depending on the oscillations that are generated by similar objects on other affine planes. We study some typical structures that arise when the oscillations’ amplitudes tend to zero, and show that the state of each such structure at any value of \(t\) can be associated with a real parameter \(0 \leqslant \beta < 1\), and that a special type of interaction with other similar structures exists which results in readjusting the value of \(\beta \). We go on to think of \(R^3\) at any value of \(t\) as corresponding to a hypersphere in \(R^4\) via the stereographic projection, where \(t\) is identified as the logarithm of hypersphere radius in the foliation of \(R^4\) in concentric hyperspheres. This leads to interpreting some curves arising from the structures we study as corresponding to certain \(S^2\) curves. We use both sides of that last correspondence to derive the free Dirac equation as the classical equation of motion of an abstract point particle, where our typical structures and their interactions are understood in connection with electrons interacting with an em radiation field, and the emergent description of any point in spacetime typically involves an infinite number of discrete values of \(t\). The Dirac equation is thus derived from the Frenet equations of our special family of curves, and the physical meaning is determined by the identification of physical and geometrical entities required by the derivation. We propose that the origin of the infinitesimal oscillations in our theory has to do with the axiomatization of the Euclidean plane and the construction of the real numbers. We briefly discuss the relevance of these ideas to the strong interaction and to gravity.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction and general outline
The conjecture presented here is that the fundamental notions of physics, including such basic concepts as spin, charge(s), mass and spacetime, may emerge from a mathematical theory having to do with rotations in \(R^4\) and fluctuations in the metrics of 2-manifolds. The work is in its early stages, and my purpose is to point out the direction which, I believe, needs to be explored, and present a few of the questions that arise. The first preliminary fragments of a possible physical picture that are starting to emerge seem to hold the promise of good (though not perfect) agreement with some physical theories, especially QED. Although the crux of the current work is the possible connection with QED, more unsettling implications already seem to be indicated in respect to some other subjects. We begin with a general outline of these ideas, starting with an introductory discussion of the mathematical concepts involved.
An object called an “Elementary Metric Oscillator” (EMO) will be introduced, alongside the related concept of “Elementary Metric Oscillator Space”. Many questions still need to be answered before EMO space and the language we use to discuss it can be said to be well defined. Much of what we do here is a first effort to elucidate these questions.
Let’s first think of stereographically projecting the punctured hypersphere \(S^3\backslash ( - 1,0,0,0)\) onto \(R^3\):
We think of this as a way of representing the unit hypersphere in \(R^3\): The point \((1,0,0,0)\) is represented by \((0,0,0)\), and \(( - 1,0,0,0)\) is represented as the limit at infinity in all directions. Any straight line through \((0,0,0)\) represents a punctured great circle on the plane \(x_1\), \(y\), where \(y\) is a unit vector in the hyperplane \(x_2\), \(x_3\), \(x_4 \). The unit sphere in \(R^3\) represents the unit sphere in the hyperplane \(x_2\), \(x_3\), \(x_4 \). Any plane through \((0,0,0)\) represents the punctured unit sphere in a hyperplane \(x_1\), \(y\), \(z\), where \(y\), \( z\) is a basis of a plane contained in the hyperplane \(x_2\), \(x_3\), \(x_4 \).
Take the standard basis of \(R^3\) and choose a point in \(R^3\) and an orthonormal right-handed affine basis with the chosen point as origin. The choice of point and basis determines a translation and a rotation of the standard basis. All the possible choices constitute the group of solid motions \(R^3\times SO(3)\). Considering \(R^3\) as representing \(S^3\backslash ( - 1,0,0,0)\) we get a group of diffeomorphisms from \(S^3\) onto itself isomorphic to \(R^3\times SO(3)\).
The group we’ve just defined induces a group of diffeomorphisms between punctured spheres which is also isomorphic to \(R^3\times SO(3)\): We choose as a convention a plane spanned by 2 of the vectors in the standard basis of \(R^3\), and think of the 2 basis vectors as a basis of the plane. We look at the translation and rotation that this basis undergoes as a result of a given translation/rotation of the \(R^3\) basis. Considering \(R^3\) as representing \(S^3\backslash ( - 1,0,0,0)\) this determines a mapping between a punctured unit sphere contained in \(S^3\) and some punctured sphere of radius \(0 < r \leqslant 1\) contained in \(S^3\). Similarly looking at all the possible translations/rotations of the standard basis in \(R^3\) we get a group of mappings between punctured spheres, isomorphic to \(R^3\times SO(3)\).
Let us now define a global parameter \(t \in R\) so that instead of \(R^3\) representing \(S^3\backslash ( - 1,0,0,0)\) we now have \(R\times R^3\) representing \(R\times S^3\backslash ( - 1,0,0,0)\). We also think of this in the following, more elaborate, way: We take the foliation of \(R^4\) in concentric hyperspheres, and denote the hyperspheres by a parameter \(t = \ln r\), where \( r\) stands for the radius in \(R^4\). Given a value of \(t\), we normalize the hypersphere with radius \(\mathrm{e}^t\) to radius 1, and then stereographically project the punctured normalized hypersphere onto \(R^3\). We can thus think of \(R\times R^3 \) as representing \((0,\infty )\times S^3\backslash ( - 1,0,0,0) \). We will occasionally need to refer to this point of view, while on other occasions we’ll just think of an \(R\times S^3\backslash ( - 1,0,0,0) \) structure.
The mappings between punctured spheres we’ve defined are of special interest, because defining them is the first step toward a definition of an Elementary Metric Oscillator. That definition too will involve determining an affine plane in \(R^3 \) and a basis for that plane. The origin of the affine basis will be called the EMO focal point. Similarly to the notions we’ve already seen, manipulating EMOs will involve translating the focal point and rotating the basis vectors, so that the state of a given EMO corresponding to a given value of the parameter \(t \) will be determined by the 6 parameters of \(R^3\times SO(3) \). We will shortly introduce 2 additional parameters which determine the way a given EMO acts on other EMOs.
It is convenient to use the metaphor of \(t \) being “the time in EMO space”, so that we can talk of the state of a given EMO at a given time, or equivalently, of the momentary state of a given EMO. This is just a convenience of language, and \(t \) must not be confused with physical time. We will discuss continuous changes in the states of EMOs, and, using the language where \(t \) is thought of as time, we will think of these changes as continuous motions of EMO focal points and rotations of EMO planes.
It follows that the momentary rate of change in the state of a given EMO is given by six parameters—the momentary linear velocity of the focal point (a vector in \(R^3) \) and three angular velocities determining the rotation that the EMO plane is undergoing at the given moment. Given these six parameters we can determine a frame of reference where the given EMO is momentarily at rest, that is, its focal point is not moving and its plane is not rotating.
For the sake of the following discussion, let’s assume that we are given a full description of EMO space at a specific value of \(t \), aka a specific moment, and according to this description, EMO space contains exactly 2 EMOs. At this point in our discussion this amounts to saying that we are given 2 sets of 6 parameters, each determining the momentary state of an EMO. As already mentioned, we will soon define the action of an EMO on other EMOs. From that definition it will follow that, given the 2 sets of 6 parameters, it may not be possible to assume that one EMO is at rest relative to the other because, depending on the exact values of the given parameters, one EMO may momentarily act on the other, causing the focal point of the EMO acted upon to move and its plane to rotate. It may also happen that both EMOs momentarily act on each other. We are aiming at a picture where, given a momentary description of EMO space with a finite number of EMOs in it, there should exist one and only one reference frame, which we shall call the natural reference frame, where the momentary velocities of the focal points and angular velocities of the planes of all the EMOs should be accounted for by the action of the EMOs on each other, that is, the interaction between EMOs. In other words, we aim at a picture where the motion of EMO focal points and rotations of EMO planes can be construed as emanating from the interaction between EMOs. In the case of the above example, where we assumed EMO space contained exactly 2 EMOs, we should be able, in the natural reference frame, to deduce the 12 parameters pertaining to the rate of change of the EMO states from the 12 parameters determining the states, together with the (not yet specified) parameters determining each EMOs action.
The phrasing used above, where I considered the number of EMOs in EMO space to be a part of some given initial conditions, may be a little misleading: In fact, we will work on the assumption that the number of EMOs does not depend on \(t \), that is, we will not consider the possibility of EMOs being created or destroyed, but rather, we will study some typical structures that occur as a result of the interaction between EMOs, and we will think of these structures as EMO combinations, which, in turn, can be created or destroyed. We will eventually see that our results may depend on assuming a finite number \(n \) of EMOs in EMO space and studying the typical structures that can be observed under certain assumptions, which imply, among other things, that \(n \) be large, in a sense that will be discussed.
Since we assume the motion of EMOs to be determined by their interactions, it should be possible, given \(6n \) initial conditions at some \(t \) (the momentary states of all the EMOs) together with the parameters that determine all the EMOs’ actions, to determine the EMO states at any other \(t \). The reader is however warned not to expect this to lead to a deterministic physical picture: We will see later that the EMO theory description of any point in spacetime might involve an infinite number of values of \(t \), and these values cannot be assumed to be contained in any one segment of the \(t \) line. So, assuming a finite number of EMOs, we will eventually conclude that physics is non-deterministic because determining the value of any physical variable requires infinite calculations. We shall however propose that the idea of the quantum measurement has to do with something happening at a specific value of \(t \).
The first step toward a definition of EMO interaction is to define the conditions that allow an EMO, which we shall denote (a), to act on another EMO, denoted (b). The basic rule is that, on the side of the acting EMO, EMO action is mediated by the EMO plane, and on the side of the EMO acted upon, EMO action is mediated by the EMO focal point. This means that EMO (a) can act directly on EMO (b) at a given \(t \) only if focal point (b) is in the EMO (a) plane [aka is on plane (a)] at that \(t \). So the focal point of an EMO can be thought of as a handle that other EMOs will take hold of to manipulate it. However, EMO (a) can act on EMO (b) indirectly, by acting on some other EMO (c) whose focal point is momentarily on the EMO (a) plane, if at that moment the (b) focal point is on the (c) plane. And, of course, longer chains of influence are possible.
The exact definition of the EMO action will be given later. We will then start by defining EMO (a)’s effect on the positions of test particles placed randomly on its plane, where the test particles will be understood to be the focal points of EMOs which do not act on EMO (a) or on each other (The question of the rotation of EMO planes, we will later see, is a little more subtle than the question of the motion of focal points). The general idea will be that each EMO generates oscillatory motion along each of the concentric circles on its plane (with the focal point as center). All the test particles placed on any radial half line from the focal point oscillate together, no matter how far they are from the focal point. A phase difference is defined between the oscillations of different half lines so that the structure generated on the EMO plane resembles one cycle of a longitudinal wave (sound wave) which had been bent into a circle. The wave phase progresses azimuthally round the focal point. We’ve said that the EMO state depends on the 6 parameters of \(R^3\times SO(3) \), but it may not have been quite obvious why the EMO would not be invariant under rotations round an axis perpendicular to its plane and intersecting it at the focal point. It is now clear that such a rotation will cause (and be equivalent to) a change of the phase of the oscillations generated by the EMO. Note also that the direction in which the phase of the oscillations progresses as a function of \(t \) can be used to assign the EMO plane an orientation.
Thinking of the correspondence between EMO space and \(R\times S^3 \) we have that, for an EMO whose focal point is resting at the origin of \(R^3 \) and whose plane is not rotating (apart from the rotation implicit in the continual progression of the EMO oscillatory action), the motion generated by the EMO action represents motion along parallels (lines of constant latitude) on the sphere in \(S^3 \) which is represented by the EMO plane. If the EMO is at rest in another state, that is, its focal point has been translated to another point in \(R^3 \) and its plane has possibly been rotated, then to find the motion represented by the EMO-generated oscillations we need to find what the corresponding mapping between spheres in \(S^3 \) (represented by the translation and rotation which produce the new state) does to the lines of constant latitude of the original sphere. Solving this in a general way is not needed for what we do here; I think it is not difficult to see that if the straight line passing through the EMO focal point and the origin of EMO space is perpendicular to the EMO plane, then the mapping between spheres preserves the lines of constant latitude, while taking each such line to another, and that in the more general case the parallels are not preserved.
If the EMO is in motion, that is, if the focal point has a velocity different than zero, which is given as a vector in \(R^3 \), and/or the plane is rotating in some way which is given in terms of angular velocities around axes, we need a rule to tell us if and how the internal structure of the EMO depends on the momentary velocity and angular velocities. In other words, the question is whether the angular velocities that the EMO generates on its plane change because the entire EMO plane is moving, and if so, how. I will later describe the transformation rule of EMO-generated angular velocities which is in fact needed to get the physical results, and I’ll try to make sense of it mathematically. This will involve somehow associating the flow of the EMO phase with the Hopf flow in \(S^3 \). There are still many open questions in this regard.
Similarly to the general description now given, the exact definition of the EMO action will be given in terms of its effect on test particles representing the focal points of other EMOs. But I will also briefly consider a different point of view, thinking of the oscillations generated by an EMO as the oscillations of the geodesics of a 2-manifold formally identified with the EMO plane. That is the origin of the term EMO.
The two parameters which determine an EMO’s action are the angular amplitude of the oscillations generated by the EMO, denoted by \(\varepsilon \), and the maximum angular velocity, achieved in the middle of the oscillations, which is \(\varepsilon \omega \), where \(\omega \) stands for the angular phase velocity of the EMO-generated wave. In the framework suggested here, \(\varepsilon \) and \(\omega \) are considered constants of the EMO, that is, they don’t change with \(t \). For the EMO definition to work we need to stipulate that \(\varepsilon \) be small in relation to any angle involved in the phenomena we wish to study. When talking about the phases of EMO-generated oscillations I will usually use mod\((2\pi ) \) language, for example, referring to the beginning of a cycle as \(\omega t=0\).
Our work will revolve largely around an object constructed as a combination of four EMOs. The term “object” should be taken here with a grain of salt, since what we do is single out a structure involving 4 EMOs from a possibly much more complicated structure these 4 EMOs are a part of. It will be stipulated that all the EMOs in a given object of this kind share the same values of \(\varepsilon \) and \(\omega \), and that \(\varepsilon \ll \frac{\pi }{4}\), since the angle \(\frac{\pi }{4} \) plays an important part in the structure of the new object. We will also need to stipulate \(\varepsilon d = \sqrt{2} \), where \( d \) is the distance between 2 of the focal points defining the new object. We will not stipulate anything about the value of \(\varepsilon \) by itself, except for \(\varepsilon \ll \frac{\pi }{4} \), so we are in fact interested in a range of objects with small \(\varepsilon \)’s and large \(d \)’s, satisfying \(\varepsilon d = \sqrt{2} \) . I’m less clear about the value of \(\omega \). We will in fact see an argument for \(\omega \) being a universal constant of all the EMO combinations of interest, but I’m not sure how strong the argument is, and even if it is strong, it does not preclude the existence of EMOs with other values of \(\omega \), as long as we restrict our study of EMO combinations to one equivalence class of EMOs with a given value of \(\omega \) (where we think of the equality of \(\omega \)’s as an equivalence relation).
We will also deal with a special class of interactions involving our 4-EMO object and an external EMO. The effect of the interaction on the object will only depend on the momentary angular velocity generated by the external EMO at a point identified as the effective focal point of the 4-EMO object. Therefore, these interactions will never depend on the \(\varepsilon \) or \(\omega \) values of the external EMO separately, but only on the product \(\varepsilon \omega \Phi \), where \(\Phi \) is the momentary phase of the external EMO. This is at least one reason why, even if all the EMO combinations studied share the same \(\omega \), there is still need to consider the existence of other EMOs with different \(\omega \)’s.
The 4-EMO combination mentioned above is an example of a stable EMO combination, where, by requiring that the combination be stable, we mean that it have internal degrees of freedom giving it enough flexibility to withstand at least some interactions with external EMOs, without losing those characteristics that make it identifiable as a combination. In naming the parts of the 4-EMO combination I will resort to car imagery: First there’ll be the body of the combination, consisting of two EMOs sharing the same plane, with a distance \(d \) between their focal points, and a specific phase difference between them. And then there’ll be the wheels, which are two additional EMOs on planes perpendicular to the body plane and to each other. The job of the wheels will be to rotate the body plane, keeping the combination intact.
We will divide the interactions involved into 3 types:
-
Type (i): The internal interactions between the 4 EMOs of which the combination consists. Studying these interactions will lead to the identification of a point effectively functioning as the focal point of the entire combination. The internal state of the combination will be given by three discrete binary parameters, two pertaining to the state of the body and one pertaining to the state of the wheels, and additionally, one real parameter \(0 \leqslant \beta < 1 \) describing the relation between the body and the wheels. We will first study the case \(\beta = 0 \) and see that the wheels are then neutralized and that in some sense the effective focal point can be said to be moving in a circle of radius \(\frac{\varepsilon d}{\sqrt{2} } \) on the body plane. In the case \(\beta > 0 \), the wheel action rotates the body plane round the momentary tangent to that circle, and, in the same limited sense, the effective focal point can be said to be moving in EMO space along a helix whose torsion is proportional to \(\beta \).
-
Type (ii): We will identify a special kind of interaction between our 4-EMO combination and an EMO external to the combination. The interaction respects the internal structure of the combination and results in readjusting the value of \(\beta \). Several conditions must be met momentarily for such an interaction to take place: The plane of the external EMO must momentarily be on the plane of one of the wheels, with the external focal point, the wheel focal point and one of the body focal points all positioned on the same straight line, and all this must happen exactly when the phase of the combination is \(n\pi / 2 \). Apart from changing the value of \(\beta \), the interaction might also translate the entire object along a distance which cannot be deduced from the before and after \(\beta \) values. We will mostly be interested in the case where the external EMO is a wheel of a similar combination and the conditions specified are met by both combinations involved. These interactions constitute a very small fraction of the interactions in EMO space.
-
Type (iii): All the other interactions, which will be treated in some limited sense as a background noise of random fluctuations. The fluctuations may be very fast, since the velocities generated by an EMO are proportional to the distance from its focal point.
As we said, in the case \(\beta = 0 \) the curve along which the effective focal point moves can be interpreted in some sense as a circle. Thinking of EMO space as representing \(R\times S^3\backslash ( - 1,0,0,0) \), we might, in principal, find out exactly what curve in \(S^3 \) is represented. We will need, however, a slightly different procedure, which we will call the wandering EMO procedure. This will produce a curve in \(S^2 \) encoding some information, not only concerning the motion of the effective focal point, but also some other aspects of the body plane. My understanding of this step in my argument is still insufficient. Roughly speaking, what we do is ask the following question: supposing that the movement of the effective focal point was caused by rotations and translations acting on a single EMO, rather than the more complicated structure of the body plane, what rotations in \(S^3 \) would then be represented? The curve in \(S^2 \) that we get, given some arbitrary choice of the discreet parameters, and with the additional stipulation of \(\frac{\varepsilon d}{\sqrt{2} } = 1 \), is the following, written here in \(R^3 \) coordinates:
We will study some characteristics of this curve and consider some characteristics of the various curves produced by rotating or reflecting it. We will also ask how these various curves would change if we changed the value of \(\beta \). The answers to these questions will constitute the basis of our physical discussion.
If we think of this curve as describing the motion of an abstract point particle, then at every \(t \) separately the particle can be thought of as rotating with angular velocity \(2\omega \) on the unit circle of the momentary plane \(x,|{\cos (\omega t)}|y + \sin (\omega t)z \). From this point of view, the curve represents a point particle rotating with angular velocity \(2\omega \) round the rim of a rigid disk which in itself is oscillating with angular velocity \(\omega \) round the \(x \) axis, which is contained in the disk. (This simple picture is achieved thanks to the stipulation \(\frac{\varepsilon d}{\sqrt{2} } = 1 \). I think any other radius would have given a more complicated curve. This is expected to eventually determine physical scale and be understood in connection with the electron’s reduced Compton wavelength).
The next step in the argument may seem rather surprising: We identify the momentary plane \(x,|{\cos (\omega t)}|y +\sin (\omega t)z \) with the body plane, and accordingly identify the 3-dimensional space in which this plane oscillates with EMO space, separately at each moment. I suspect this step in the argument may not be as arbitrary as it seems, because it somehow reflects the fact that the correspondence between the momentary picture of EMO space and \(S^3 \) is mediated by EMO planes. In some sense we can think of this as EMO space oscillating with angular velocity \(\omega \) relatively to the abstract \(R^3 \) space the coordinates of which we used to write the curve. We will call that space the wandering EMO space. Note that the oscillation of EMO space relative to the wandering EMO space is determined individually for each EMO combination, so that by identifying the body plane with the momentary \(x,|{\cos (\omega t)}|y+\sin (\omega t)z \) plane we have effectively added a hidden (compact) dimension to our theory.
At this point we shall start discussing the possibility of identifying some of the variables involved with physical variables. The starting point will be to observe that in the \(\beta > 0 \) case, due to the identification of the momentary \(x,|{\cos (\omega t)}|y + \sin (\omega t)z \) plane with the body plane, we can reconstruct the helix along which the effective focal point moves in EMO space as a momentary (imagined) helix with curvature and torsion \(\sqrt{1 - \beta ^2} \) and \(\beta \) in the wandering EMO space, where our \(x,|{\cos (\omega t)}|y+\sin (\omega t)z \) plane is the momentary osculating plane.
The helix torsion will eventually be interpreted as responsible for physical momentum in the direction of the binormal, while the rotation on the momentary \(x,|{\cos (\omega t)}|y + \sin (\omega t)z \) plane (the helix osculating plane) will not be interpreted in terms of movement, but rather, it will be concealed in the dynamic phase of a physical particle, with the osculating plane momentarily identified as the complex plane. This will be made possible by considering all the curves produced by rotations of the original \(\beta = 0 \) curve and assigning them suitable phase differences. Rotating the entire curve through angle \(\pi \) will be interpreted as reversing either the spin direction or the sign of the electric charge, or both, according to the choice of axis, and this will eventually be shown to be consistent with the dynamics.
There are still some questions to answer before we can fully derive the Dirac equation. I will try to show that the momentum terms in the Dirac equation emerge from the torsion terms in the second Frenet equation of our imagined momentary helix, and the mass term in the Dirac equation emerges from the curvature term in Frenet. This would be made possible by the fact that the curvature term becomes independent of \(\beta \) once we correctly identify the flow of physical time, and change variables accordingly. Physical time will thus be identified as flowing in the direction of the momentary tangent to the imaginary helix at the moment of interaction (by moment I still mean a value of \(t) \), or opposite. This last identification will be in fact deduced from the identification of the type (ii) interaction as an interaction with a photon whose wave vector points the direction from the focal point of the external EMO towards the effective focal point of the 4-EMO combination. In this sense we can say that type (ii) interactions interpret the wandering EMO space as the abstract point particle’s past light cone.These interactions are not symmetrical under the reversal of the direction of physical time.
Let me get ahead of myself: There is no identifying the abstract point particle with a physical particle. The momentary state of the EMO combination may be said to play in our description a part somewhat analogous to that which an eigenstate of the momentum operator given as one addend in a representation of the particle wave function (at a given point in space and time) plays in quantum mechanics. On the same level of general analogy, the type (ii) interactions in which the external EMO belongs to a similar combination play the part of interactions with real photons. We must note that it is not possible to establish a one to one correspondence between what we do here and any single existing physical formalism.
In the absence of interactions, the rate of the flow of physical time turns out to depend on \(\beta \) in accordance with special relativity. But consider the following: an EMO combination denoted by (a), and regarded as an observer, has at \(t_1 \) a type (ii) interaction with another combination denoted by (b). Remember that type (ii) interactions interpret (a)’s wandering EMO space as (a)’s past light cone, so from (a)’s point of view, the length of time that passed since the photon had been emitted by (b) is proportional to (b)’s momentary distance from (a) in EMO space (Here the distance between (a) and (b) is understood to be the distance between (a)’s effective focal point and (b)’s effective focal point). Now assume that the (for our purpose, random) fluctuations in EMO space contrive to bring (b) at \(t_2 \) to a distance D from (a) such that, if a type (ii) interaction were to occur at \(t_2 \), it would be regarded by (a) as an interaction with a photon emitted from (b) at the same physical time as the photon involved in the interaction that occurred at \(t_1 \). Thus, (b) can be observed by (a) to have been in two different places at the same physical moment in the past. In fact, (a) may regard (b) as having been in an infinite number of places in the same physical moment, and the values of \(t \) involved may not be contained in any finite segment of the \(t \) line. In principle, to know all the different places (b) had been at, at a given moment in physical time, (a) needs to know the continuous and infinite history at \( - \infty \leqslant t \leqslant \infty \). Actually, of course, (a) only gets discreet pieces of data through type (ii) interactions.
The current paper ends shortly after the connection between EMO space and the Dirac equation is indicated in a preliminary way, because I feel that a more rigorous treatment of all the questions presented here is required before the work can continue. The rest of the outline presented now is intended only as a general scheme for future work.
I already mentioned the analogy with the concept of a particle as a wave packet. This can now be clarified. The same argumentation that has lead us to conclude that the observer (a) may consider the observed EMO combination (b) to be in many places at the same physical moment, also shows that if (a)’s position in EMO space is fluctuating and (a) is “looking” toward one specific location in EMO space, (a) may observe many different EMO combinations coexist at the same place at the same physical time. (The circular movement of the effective focal point of our typical combination leads me to think of the EMO space positions of both observer and observed as fluctuating). This only requires that for each of these EMO combinations there exist some value of \(t \) at which (a) can observe it (that is, its effective focal point) as having been at the required location at the right physical time. Note that my thinking of (a) as “looking” toward a location in space at some moment is only a metaphor: What I mean is that for each of these EMO combinations there should exist some value of \(t \) at which (a) would observe it as having been at the required location at the right physical time, if a type (ii) interaction were to occur. The fact that many EMO combinations could be observed by (a) as being in the same place at the same physical time (but at different \(t \)’s) if a type (ii) interaction were to occur, is understood to account for quantum superposition; But (a) does not get any information about the observed combinations unless a type (ii) interaction really occurs, at one of those \(t \)’s, which is understood to account for the quantum measurement. Since it is clearly impossible to determine by calculation the properties of all, or of any finite fraction, of the observations that (a) could relate to a given point in spacetime if type (ii) interactions were to occur, the emergent physical picture must be essentially non-deterministic and rely on the calculation of probabilities.
I expect that quantum superposition would have to be understood via the vector addition of the velocities of the effective focal points of EMO combinations which are observed sharing a common body plane at a given physical time (but many different values of \(t) \) with their effective focal points effectively at the same point in physical space. This implies that we never add the velocities of the focal points of two EMO combinations that don’t share a body plane: I expect that to be understood in connection with the orthogonality of momentum eigenstates in the quantum formalism. I will comment briefly about the question of probability amplitudes later.
The study of the 4-EMO combination presented here is intended as a first step toward a full understanding of the electron. I suspect that to understand the other leptons, and the hadrons, we may have to study more complex EMO combinations. This idea will be briefly discussed towards the end of the paper, and it will be suggested that such an understanding may make it possible to calculate particle masses. I’ll also add a short discussion concerning the prospect of deducing a theory of gravity from EMO theory, and a few words about the problem of reconciling these ideas with cosmology.
I’ll finish the paper with a brief discussion of the possible origin of EMOs, and propose that EMOs may emerge naturally from a discussion of the construction of the real numbers and the geometric axiomatization of the Euclidean plane.
2 The elementary metric oscillator
We will now see a preliminary definition of a non-interacting EMO. At this stage we will not refer to the idea of EMO space representing \(S^3 \). We start with a semirigorous definition of an EMO in terms of its effect on test particles. Think of a plane P with polar coordinates \(r,\varphi \), and a series of test particles with index \( i \), placed randomly on it, avoiding the origin (of P). If, for a given period of time (aka interval on the \(t \) line) there is an EMO with its plane constantly on P and its focal point resting at the origin, and there are no other EMOs affecting the test particles, then there exist such \(r_0^i,\varphi _0^i,t_0 \) and constants \(\varepsilon ,\omega \) so that during that period the locations of the test particles are dependent on \(t \) in the following way:
\(t_ 0 \) is only needed in the definition because it is not given that the beginning of the given interval on the \(t \) line coincides with the beginning of an EMO cycle . The \(i \)’th particle oscillates on an arc with angular aperture \(2\varepsilon \). The middle of the oscillation is at \(\varphi = \varphi _0^i \). The dependence of this oscillation’s phase on \(\varphi _0^i\) ensures that we get a longitudinal wave progressing azimuthally. The angular phase velocity is \(\omega \), and for each \(\Delta \omega t = 2\pi \) the wave completes a full turn around the focal point, identified here with the origin of the plane.
We generalize this by allowing the plane to be any affine plane in \(R^3 \) with the focal point anywhere on the plane. If the choice of plane and focal point isn’t dependent on \(t \), we say that the EMO is at rest.
We can change a sign in the definition to get \(\varphi ^i(t) = \varphi _0^i + \varepsilon \cos (\varphi _0^i - \omega (t - t_0 )) \). That is equivalent, up to a phase difference, to rotating the EMO plane by \(\pi \) around some axis contained in it and passing through the focal point. If the EMO is defined this way we can call it left handed, as opposed to the right-handed EMO previously defined.
Let us calculate the dependence of the density of the test particles on \(t \).
Consider two particles with indices \(i,j\) with:
and
Mark the momentary length of the arc between the two particles \(\mathrm{dist}(\omega t) \).
Assume that \(t \) is gauged so that \(t = 0 \) coincides with the beginning of a cycle, so that one can take \(t_0 = 0 \).
We get
It follows that
At the limit \(\Delta \varphi \rightarrow 0 \) we have
It follows that the test particle density is bigger or smaller than the test particle density in the absence of an EMO by a factor of
This will be called the densification factor. The momentary velocity of each particle is \(r\omega \varepsilon \sin (\varphi + \omega t) \) (where I neglect to write the particle indices). Each particle’s velocity is maximal in the direction of the progression of the wave when \(\varphi + \omega t = \frac{\pi }{2} \), that is, when the particle is at the maximum densification. The particle’s velocity is maximal in the opposite direction when \(\varphi + \omega t = \frac{3\pi }{2} \), that is, when the particle is at the minimum densification, which means that it is momentarily in the region where the particles are the most spaced (now assuming they’d been initially equally distributed, before the EMO was introduced). At the two ends of the particle’s oscillation we have \(\varphi + \omega t = 0,\pi \) and densification factor 1, which is to say that those are the regions where the particles are distributed as they had been initially distributed.
I will now try to understand the non-interacting EMO in metrical terms. The idea is to interpret the motion of the test particles as resulting from the motion of the geodesics of some abstract 2-dimensional manifold which is identified in some sense with the EMO plane, though, clearly, not by inclusion in \(R^3 \). This implies a double interpretation of the EMO plane: Firstly, we think of it as the plane of the coordinates of some abstract 2-manifold, and secondly, we think of it as representing the manifold itself. In other words, we first think of the plane as \(R^2 \) with polar coordinates \(r,\varphi \), functioning as a static “background plane”, and then we let each radial half line angularly oscillate round its original position, so that the density of the half lines changes according to the densification factor. In the region where the density of the half lines is greater than their density on the background plane, the azimuthal length element of the abstract manifold is larger than that of the background plane. Think of two test particles positioned at the two ends of an \(r\Delta \varphi \) long arc before the EMO starts acting. Assume that at time \(t \) the two test particles are in the region where the densification factor is bigger than 1. It follows that they are closer together at \(t \), that is, positioned at the ends of an arc shorter than \(r\Delta \varphi \), assuming we are using the \(R^2 \) metric, as we are, in EMO space. But using the metric of the abstract manifold, they are always at the ends of a \(r\Delta \varphi \) long arc. So the azimuthal length element of the abstract manifold metric must be proportional to the densification factor. We conclude that the abstract 2-manifold is given by the metric:
The test particle lies on a geodesic line of the abstract manifold and oscillates with it, twice in a cycle finding itself on the associated radial half line of the background plane. There is a lot of room for confusion here, because at different points in my argument I might refer to three different kinds of angles: First, there is \(\varphi \), which denotes an oscillating half line using the angle associated with it on the background plane. Then there’s \(\varphi + \omega t \), which is the momentary phase of the half line’s oscillation. And finally there is the actual momentary angle of the geodesic on the EMO plane, \(\varphi + \varepsilon \cos (\varphi + \omega t) \).
In the next section, we will consider the oscillations generated by EMOs from a slightly different point of view, which I find a little more helpful when trying to understand the behavior of moving EMOs. I don’t yet fully understand how these different points of view correspond, or how they relate to the possibly deeper understanding of the origin of EMOs which will be proposed in the last section of the paper.
3 Interacting EMOs
It is not completely evident in what sense it would be possible to go on identifying EMO space with \(R^3 \) once we allow EMOs to interact. In principle, when studying the simplest interactions, we will want to remain in what we called the natural reference frame, that is, a reference frame where every velocity is accounted for in terms of the azimuthal oscillations generated by one of the EMOs involved. However, the discussion of EMO combinations will also lead us to adopt other, more convenient frames of reference. In EMO space the change of frame of reference will simply involve the vector addition of velocities, plus a transformation rule for the azimuthal angular velocities. But one must remember that even the simplest translation in EMO space represents some diffeomorphism in \(R\times S^3\).
Eventually, after studying our 4-EMO combination in EMO space, we will be faced with the challenge of interpreting our results in terms of some structure in \(R\times S^3 \). At that point we will have to consider using a frame of reference in which some focal point of interest remains immobile and is considered the origin of EMO space, so that the mapping between EMO space and \(R\times S^3 \) be well defined. The current work will only involve one instance of this kind of problem, which will be resolved in a manner slightly different from what I have just suggested, using the wandering EMO procedure. As mentioned before, there is still a great deal that I don’t understand about that particular step in my argument.
We already said that when a focal point of an EMO (a) is found on the plane of some other EMO (b), it is carried around with the oscillations of the (b) radial half line on which it lies [so it moves on a circle whose center is focal point (b)]. I assume that focal point (a) is carried by the (b) half line indefinitely, even if the (b) plane itself is moving under some other influences, unless focal point (a) is eventually snatched away by some third EMO (c) which has (in the natural reference frame), at some moment, a larger velocity at focal point (a) than the velocity of EMO (b) at focal point (a). I am referring here to the momentary linear velocities, not to angular velocities, so generally, EMO (c) has a good chance of snatching (a) if the distance between its focal point and that of EMO (a) is greater than the distance between focal points (a) and (b). The velocities generated by an EMO are proportional to the distance from its focal point, but, assuming for the sake of discussion that focal points are equally distributed in EMO space, the number of influencing EMOs may grow as the square of the distance. Therefore, assuming a picture where EMO (a) is only acted on by other EMOs but does not act on them, one couldn’t reasonably expect EMO (c) to keep its hold on focal point (a) for very long. As we will soon see, all these considerations change considerably if one thinks of EMO (a) reciprocating and acting on focal point (c) or (b). In any case, the question of two EMOs (b) and (c) competing over some focal point (a) is at this time hypothetical, and will not appear in the simple situations we will encounter.
All the situations we deal with will involve mutual interactions, which means that when EMO (a) is acting on focal point (b) EMO (b) is also acting on focal point (a). More specifically, our 4-EMO combination will be based on two basic kinds of interaction. The first is an interaction between two EMOs which share the same plane. Evidently in this case each focal point lies on the other EMO’s plane, and the motion is restricted to that plane, so that in the absence of other influences the plane’s identity is preserved—for example, it remains the \(x\), \(y \) plane at any \(t \). We will only investigate the one situation we need, defined by a \(\frac{\pi }{2} \) phase difference between the two EMOs.
The second situation we’re interested in is the interaction of two EMOs with orthogonal planes where it is given that the focal point of each EMO lies on the other EMO’s plane. In this case the momentary motion can be described in terms of the combination of the momentary rotation of plane (a) round an axis perpendicular to plane (b) and intersecting it at focal point (b) [and contained therefore in plane (a)], and the momentary rotation of plane (b) round an axis perpendicular to plane (a) and intersecting it at focal point (a) [and contained therefore in plane (b)].
In such cases as now described, the question of the rotations of the EMO planes is, in principle, relatively simple: In the first situation the plane is constant, apart from possible rotations around axes perpendicular to it, and in the second situation the overall rotation of the plane can be deduced from the momentary angular velocity of the rotation of plane (a) round an axis perpendicular to plane (b) and that of the rotation of plane (b) round an axis perpendicular to plane (a). However, it is not obvious what the rule is in the general case: Suppose focal point (a) is on plane (b) but focal point (b) is not on plane (a). Focal point (a) has a momentary velocity determined by its distance from focal point (b) and by the angular velocity of the (b) half line it’s on, but what about plane (a)? Is it rotating? The obvious answer seems no, but at this time I know no way of establishing this for certain. Such questions may be in some sense hypothetical: Since the interactions between EMOs cause planes to rotate, and an interaction can only be stopped by some other interaction, the probability of any given EMO being connected to any other given EMO through some chain of influences at a given moment is probably 1. So we can reasonably assume that EMO space contains just one huge connected component. Still, for the sake of practical calculations, one would probably want to have some idea of how EMO planes rotate during non-mutual interactions.
We now address the main subject of this section: We want to know if and how the angular velocities generated by an EMO change when the EMO is in motion. Given a specific EMO with specific values of \(\varepsilon \) and \(\omega \), the momentary states of the EMO constitute an \(R^3\times SO(3) \) group. It is therefore natural to think of the momentary motion of the EMO in terms of the momentary velocity of the focal point, given as a vector in \(R^3 \), and the momentary angular velocities of the EMO plane’s rotation round axes passing through the focal point.
It turns out that the following proposition is required and sufficient for the work we do here, though it may not be detailed enough to deal with any possible EMO motion:
-
(a)
The angular velocities generated by an EMO do not depend on the momentary linear velocity of the focal point and the momentary angular velocity of rotation round an axis perpendicular to the EMO plane and intersecting it at the focal point. This means that if it is given that the focal point has some momentary velocity \({\varvec{u}}\), given as a vector in \(R^3 \), we just do the vector addition at every point on the EMO plane, adding \({\varvec{u}} \) to the linear velocity generated by the EMO oscillation at that point (which is \(\varepsilon \omega r\sin (\varphi + \omega t) \) in the azimuthal direction). If it is given that the EMO plane is rotating with angular velocity \(\mu \) round the axis perpendicular to it at the focal point, in the direction of progression of the EMO phase, we add \(\mu \) to the momentary angular velocity of every radial half line (which is \(\varepsilon \omega \sin (\varphi + \omega t)) \).
-
(b)
If it is given that the EMO plane is momentarily rotating with angular velocity \(\mu \) round an axis contained in the EMO plane and passing through the focal point, all the angular velocities generated by the EMO are diminished by the factor:
$$\begin{aligned} \sqrt{1 - \left( {\frac{\mu }{\varepsilon \omega }} \right) ^2} \end{aligned}$$
I don’t fully understand the reason for this rule (which may simply exist in order to allow the natural reference frame to be differentiated from rotating ones), but the following discussion may help a bit. Let’s consider an EMO at rest on the \(x\), \( y \) plane with the focal point at the origin. The azimuthal angular velocities are \(\varepsilon \omega r\sin (\varphi + \omega t) \), so that at \(\omega t = n2\pi \) the velocity is zero at \(\varphi = 0 \) and maximal at \(\varphi = \frac{\pi }{2} \). Up to an angular deviation of \(\varepsilon \) this means that the velocity is zero on the \(x \) axis and it is maximal on the \(y \) axis. This entire picture rotates round the \(x\), \(y \) plane with angular velocity \(\omega \). Interpreting this as representing flows in \(R\times S^3 \), we get that, up to an angular deviation of \(\varepsilon \), what we see momentarily at each \(t \) is the projection, on the parallels of the sphere represented by the EMO plane, of a flow with angular velocity \(\varepsilon \omega \), which is directed in the \((0,0, - 1,0) \) direction at \(\omega t = n2\pi \). And the entire picture rotates with angular velocity \(\omega \) round the \(x_3,x_4 \) plane. Of course, we can replace \(x_3,x_4 \) by any other plane in the hyperplane \(x_2,x_3,x_4 \), simply by rotating the EMO plane.
This seems to imply that the wave structure of the EMO is designed to represent some flow given by a rotation with angular velocity \(\omega \) on a great circle in \(S^3 \), which, in our example, would be the great circle at the intersection of \(S^3 \) with the \(x_3,x_4\) plane. We need the momentary \(\varepsilon \omega \) flow and its projections on all the directions to generate the bigger picture of the \(\omega \) flow, corresponding to the progression of the longitudinal wave phase in EMO space. The transformation rule suggested above ensures that when we are in the process of rotating the plane, say from \(x_3,x_4 \) to \(x_2,x_3 \), we keep the phase velocity constant, so that at any moment the EMO represents an \(\omega \) flow in the \(x_2,x_3,x_4 \) hyperplane. On the other hand, rotations that only change the phase of the flow on the great circle, leaving the circle invariant, can be added freely, not at the expense of the rate of the original flow. Also, rotations of the entire hyperplane, changing it into another hyperplane, can be added freely.
It is now convenient to recall the idea of EMOs representing some structures in \(R^4 \), with \(t = \ln r \). If we want to assign the parameter \(t \) a direction in \(R^4 \), it has to be the direction of the \(x_1 \) axis, so that all the possible flows on great circles in the \(x_2,x_3,x_4 \) hyperplane be orthogonal to it (otherwise we could not speak of flows at all). So the picture we get for our original example is of a flow along a logarithmic conical helix contained in the \(x_1,x_3,x_4 \) hyperplane, with the \(x_1 \) axis as the helix axis.
If we now think of some general EMO at rest, and we want to see EMO space from that EMO’s point of view, we have to think of that EMO’s focal point as the origin of EMO space and think of the new EMO’s plane as resting on the \(x,y\) plane. What does such a transformation involve, in \(R^4 \)? It now appears that the location of the EMO focal point determines the direction of \(t \) (to replace the \(x_1 \) choice of our original example), and consequently, it determines a hyperplane orthogonal to that direction (as was \(x_2,x_3,x_4 \) determined in our original example). The direction of the EMO plane determines a plane in the above hyperplane (as was \(x_3,x_4\) determined in our original example), and consequently, the hyperplane in which the helix is contained is determined (as was \(x_1,x_3,x_4 \) in our original example).
The idea of a flow on great circles in \(S^3 \) with an invariant angular velocity \(\omega \) seems to resonate with ideas connected with the foliation of \(S^3 \) in Clifford parallels (aka the Hopf fibration). Let’s think of \(S^3 \) in Hopf coordinates:
where \(0 \leqslant \alpha < \frac{\pi }{2} \), \(0 \leqslant \eta < 2\pi \), \(0 \leqslant \theta < 2\pi \).
This specific choice of a Hopf fibration is given by the choice of the two completely orthogonal planes \(x_1,x_2 \) and \(x_3,x_4 \) (planes are completely orthogonal if any vector in one plane is orthogonal to any vector in the other) and by the choice of the phase of the Hopf flow determined by \(\theta \). (Substituting \(\theta + \Delta \theta \) for \(\theta \) would constitute a change of phase). Each Hopf circle is given by a choice of \(\alpha \) and \(\eta \), and has a projection of radius \(\cos \alpha \) on the first of the two completely orthogonal planes and a projection of radius \(\sin \alpha \) on the second. The value of \(\eta \) determines the phase difference between the two projections. The Hopf flow itself is achieved by letting \(\theta \) run from \(0 \) to \(2\pi \) on all the circles.
\(S^3\) is parallelizable since, given some specific Hopf flow, we can find two Hopf flows which are orthogonal to it and to each other at every point. Suppose we choose, as a convention, to always regard the vector \((1,0,0,0) \) as belonging to the first of two completely orthogonal planes, and always choose the phase so that \(\theta = 0 \) coincides, on the first plane, with the direction \((1,0,0,0) \). We then have the two following Hopf fibrations which are orthogonal to the one above and to each other:
First we have
where the two completely orthogonal planes are \(x_1,x_3 \) and \(x_4,x_2\).
And then we have
where the two completely orthogonal planes are \(x_1,x_4 \) and \(x_2,x_3\).
Seeing that we predetermined the phase and the role of \(x_1 \) as a vector in the first plane, these two last fibrations were determined simply by the choice of the second plane: \(x_4,x_2 \) in the first case and \(x_2,x_3 \) in the second. This is equivalent to the situation in EMO space, where, with our original choice of focal point, we could choose our EMO’s oscillations to be generated by a rotation on \(x_3,x_4 \) or, orthogonally, \(x_4,x_2 \) or, orthogonally, \(x_2,x_3 \).
Going back to our logarithmic conical helix, we can now see that the choice of helix axis is equivalent to our predetermination of \(x_1 \) as belonging to the first plane (or equivalently, the choice of \(x_1 \) as the real axis of the quaternions, if we think of the multiplication by \(i \) as generating the Hopf flow). Given a choice of phase, our choice of a plane perpendicular to the helix axis is equivalent to the choice of the second completely orthogonal plane of the fibration. So, the intuitive meaning of our transformation rule seems to be that when you want to move from one fibration to another, inside the \(S^2 \) space of possibilities available to you once the helix axis and phase have been fixed, you need to use the Hopf flow itself to make the transition, rather than introduce some extraneous flow, alien to the structure of \(R^4 \). One reason why I like the idea that the Hopf flow should play such an important role in our discussion is that I hope this could be a first step towards understanding why we are working in \(R^4 \), rather then more generally in \(R^n \), or with some other specific value of \(n \).
4 A stable EMO combination
Let us think of two EMOs denoted by (1) and (2) and coexisting on the same plane. We assume a \(\frac{\pi }{2} \) phase difference between them and a distance \(d \) between the focal points. The directions of the velocities generated by EMO (1) at focal point (2) and by EMO (2) at focal point (1) are parallel or anti-parallel, and perpendicular to the segment between the focal points, therefore \(d\) is constant. (I will often use the term “the EMO’s azimuthal velocity at point \(x\)” interchangeably with “the velocity generated by the EMO at point \(x\)”). These velocities are restricted to the plane of the EMOs, so this plane is constant too. We’ll call it the body plane.
Let the position of focal point (1) be \(x_1(t),y_1 (t)\), and that of focal point (2) \(x_2 (t),y_2 (t)\), where \(x,y\) are the coordinates of a static background plane identified at some initial moment with the body plane. Define \(\left( {{\begin{array}{*{20}c} {x_ - } \\ {y_ - } \\ \end{array} }} \right) = \left( {{\begin{array}{*{20}c} {x_1 - x_2 } \\ {y_1 - y_2 } \\ \end{array} }} \right) \). (All the variables depend on \(t)\). We have \(\sqrt{x_ -^2 + y_ -^2}=d\). Define \({\hat{n}} = \frac{(x_ -,y_ - )}{d} \). So \({\hat{n}}\) is a unit vector pointing the direction from focal point (2) to focal point (1). Define \({\hat{m}}=\frac{(y_ -, - x_ - )}{d} \). \({\hat{m}} \) is a unit vector parallel or anti-parallel to the momentary velocities of the two focal points. \(\{{{\hat{m}},{\hat{n}}}\}\) is an orthonormal base of the plane. Define \(\left( {{\begin{array}{*{20}c} {\bar{x}} \\ {\bar{y}} \\ \end{array} }} \right) = \frac{1}{2}\left( {{\begin{array}{*{20}c} {x_1 + x_2 } \\ {y_1 + y_2 } \\ \end{array} }} \right) \). So \({\bar{x}},{\bar{y}} \) is the middle of the line between the focal points. Define \(\left( {{\begin{array}{*{20}c} {x_ + } \\ {y_ + } \\ \end{array} }} \right) = 2\left( {{\begin{array}{*{20}c} {\bar{x}} \\ {\bar{y}} \\ \end{array} }} \right) = \left( {{\begin{array}{*{20}c} {x_1 + x_2 } \\ {y_1 + y_2 } \\ \end{array} }} \right) \). Let’s write equations of motion for \(x_ -,y_ -,x_ +,y_ + \):
Let’s see how we get this. During an infinitesimal interval \(dt \) the two focal points are translated parallel or anti-parallel to the momentary direction of \({\hat{m}} \). To figure out the directions let’s think of an example: Assume \(0 < \omega t < \frac{\pi }{2} \) so that \(\cos (\omega t) > 0,\sin (\omega t) > 0 \). Assume that focal point (1) is at \(( - \frac{d}{2},0) \) and focal point (2) is at \((\frac{d}{2},0) \). We have \({\hat{n}} = ( - 1,0) \) and \(\hat{m} = (0,1) \). Let’s define the relative phase. Suppose that the two EMOs agree that \(\varphi = 0 \) lies momentarily on the \(x \) axis of the background plane. We assume that EMO (2)’s phase is \(\frac{\pi }{2} \) ahead of EMO (1)’s phase. Up to a global phase change we can determine that on the \(\varphi = 0 \) of both EMOs, identified as the positive direction of the \(x \) axis, phase (1) is \((0 - \omega t) \) (assuming here both EMOs are right handed) and phase (2) is \((\frac{\pi }{2} - \omega t) \). But note that EMO (2) effects EMO (1) through its \(\varphi = \pi \) half line, while EMO (1) affects EMO (2) through its \(\varphi = 0 \) line. Therefore, we get that EMO (1)’s phase at focal point (2) is ahead of EMO (2)’s phase at focal point by \(\frac{\pi }{2} \).
It follows that EMO (1) momentarily generates a velocity
\(\sin (0 - (\omega t - \frac{\pi }{2})){\hat{y}} = \cos (\omega t){\hat{y}} \) at focal point (2).
And EMO (2) generates a velocity
\(\sin (\pi - \omega t)( - {\hat{y}}) = (\sin (\omega t))( - {\hat{y}}) = - \sin (\omega t){\hat{y}} \) at focal point (1)
The minus sign in this last statement comes from the direction of progression of EMO (2)’s phase at focal point (1). (This consideration is separate from the phase difference considerations). So one end of the segment between the focal points, at focal point (1) is translated by \( - \varepsilon \omega d\sin (\omega t)\mathrm{d}t{\hat{y}} \), and the other end, at focal point (2), is translated by \(\varepsilon \omega d\cos (\omega t)\mathrm{d}t{\hat{y}} \). For the equation of \(\left( {{\begin{array}{*{20}c} {{\dot{x}}_ - } \\ {{\dot{y}}_ - } \\ \end{array} }} \right) \) we have to think of the translation of one end of the segment in relation to the other segment, which means that translations with equal signs at opposite ends will appear with opposite signs in the equation, and vice versa. Since \({\hat{m}} = \frac{(y_ -, - x_ - )}{d} = \frac{(0, - ( - d / 2 - (d / 2)))}{d} = {\hat{y}} \) and \({\hat{n}} = - {\hat{x}} \) we get the equation as written.
For the equation of \(\left( {{\begin{array}{*{20}c} {{\dot{x}}_ + } \\ {{\dot{y}}_ + } \\ \end{array} }} \right) \) we have to think of the translation of the middle of the segment between the focal points, which means that translations with equal signs at opposite ends will appear with equal signs in the equation, and we get the equation as written. Note that it is dependent on \(\left( {{\begin{array}{*{20}c} {x_ - } \\ {y_ - } \\ \end{array} }} \right) \).
Subtracting the first equation from the second we get
Adding the two equations we get
We might have deduced these equations directly from the infinitesimal translations of the focal points, but I find the reasoning presented here helpful.
If we assume left-handed EMOs we get that EMO (1) generates the velocity
\( - \sin ((\omega t - \frac{\pi }{2}) + 0){\hat{y}} = \cos (\omega t){\hat{y}} \) at focal point (2),
And EMO (2) generates the velocity
\( - \sin (\omega t + \pi )( - {\hat{y}}) = (\sin (\omega t))( - {\hat{y}}) = - \sin (\omega t){\hat{y}} \) at focal point (1).
(There is no reversal of signs because \( - \sin (\pi + \omega t) = \sin (\pi - \omega t))\).
If we go back to right-handed EMOs and change the order of the phases, so that EMO (1) is ahead by \(\frac{\pi }{2} \), we get that EMO (1) generates the velocity
\(\sin (0 - \omega t){\hat{y}} = - \sin (\omega t){\hat{y}} \) at focal point (2), and EMO (2) generates the velocity
\(\sin (\pi - (\omega t - \frac{\pi }{2}))( - {\hat{y}}) = \cos (\omega t){\hat{y}} \) at focal point (1).
If we make both changes together, that is, take left-handed EMOs and let EMO (1) be ahead, and get that EMO (1) generates the velocity
\(-\sin (0 + \omega t){\hat{y}} = - \sin (\omega t){\hat{y}} \) at focal point (2), and EMO (2) generates the velocity
\(-\sin (\pi + (\omega t - \frac{\pi }{2}))( - {\hat{y}}) = \cos (\omega t){\hat{y}} \) at focal point (1).
Let us go on with the equations of motion as written. We note that there is an irregularity in the equations whenever the coefficients (depending on \(\omega t) \) equal zero. Let’s solve the \(\left( {{\begin{array}{*{20}c} {{\dot{x}}_ - } \\ {{\dot{y}}_ - } \\ \end{array} }} \right) \) equation in some domain where it is regular, say \(\frac{3\pi }{4} < \omega t < \frac{7\pi }{4} \). The solution in this domain taken together with a computer simulation will furnish us with sufficient insight to go on.
We have
And a similar reasoning applies for the second term.
We now define
Therefore
Let’s assume, as an initial condition, that at \(t = \frac{\pi }{4\omega } \), \({\hat{n}} \) is on the \(x \) axis and \({\hat{m}} \) on the \(y \) axis. Note that
So that at \(t = \frac{\pi }{4\omega } \) we have
And the solution in the domain \(\frac{3\pi }{4} < \omega t < \frac{7\pi }{4} \) is
Figure 1 is a qualitative simulation depicting the positions of the two focal points along three cycles, with the unrealistic premise of very large \(\varepsilon \), \(\varepsilon \approx 1_\mathrm{rad} \). Each step in the simulation is represented by a black dot. I started the simulation at \(\omega t = \pi / 4 \) in order to get a symmetrical picture. The focal points start at \(( - 1,0) \) and \((1,0) \). Each focal point changes course abruptly every \(\frac{\pi }{2} \) radians, with a phase difference of \(\frac{\pi }{4}\) between the course changes of the two focal points. The velocity that the left EMO generates at the right focal point is proportional to \(\cos (\omega t) \), and the velocity that the right EMO generates at the left focal point is proportional to \(\sin (\omega t) \). The momentary velocities at any given moment are parallel in direction but generally not equal in magnitude.
Note that the symmetry of the picture is misleading, since both focal points undergo an overall “drift” to the right, accompanied by their oscillatory motion. The equation we got for \(\left( {{\begin{array}{*{20}c} {{\dot{x}}_ - } \\ {{\dot{y}}_ - } \\ \end{array} }} \right) \) was simpler than the equation for \(\left( {{\begin{array}{*{20}c} {{\dot{x}}_ + } \\ {{\dot{y}}_ + } \\ \end{array} }} \right) \) because it isolated the oscillatory motion by dealing only with the direction of the segment between the focal points. We will later see that when we take a smaller \(\varepsilon \) the drift becomes less significant in comparison with the oscillation.
If we change the order of the phases the focal points drift to the left instead of the right. Alternatively we can reverse the direction of the drift by reversing the handedness of the two EMOs, as seen in Fig. 2.
We shall come back to the binary parameters later. Let us now think of the action of the two EMOs on a test particle placed at some general point on the body plane, other than the two focal points. In fact, before discussing this let’s consider the case of a test particle placed in the intersection of two EMOs with different planes. It was already suggested that this should be understood as a competition between the EMOs over control of the test particle. Obviously there is no question of adding the velocities generated by such EMOs as vectors in \(R^3 \): Intuitively one feels that doing that would be subversive to the entire logic of EMO space, because it would lead the particle to move outside the domains of both EMOs. Remembering that we are representing some structures in \(R^4 \), or \(R\times S^3 \), the addition of two velocities generated by two EMOs that share a plane can be understood as representing vector addition in the plane tangent to the sphere represented by the EMOs’ common plane, but there is no similar interpretation for the \(R^3 \) addition of velocities from two different EMO planes.
So in the case of the body plane we add the two velocities generated at the momentary location of the test particle by the two EMOs, as vectors in \(R^2 \). And we must also remember to take into account the momentary velocities of the two focal points themselves. (There is some subtlety which I do not fully understand as to how these should contribute to the calculation, as we shall soon see). But things may become a little easier if we assume that the test particle is at distances \(r_1,r_2 \) from the two focal points, where \(r_1 \gg d,r_2 \gg d \). In such a case we can get an approximate solution by assuming that, most of the time, the velocity of the test particle is much greater than the relative velocity between the two focal points, and the direction of the test particle’s motion is almost identical to the azimuthal directions of both EMOs, which are almost the same. So, for a particle very distant from the focal points, we are aiming at an approximation where the two focal points would be replaced by some effective focal point pertaining to the combined system, and the velocity of the effective focal point would be understood as representing the motion of the entire system. Since the two directions of the azimuthal velocities of the original EMOs at any point far enough from the effective focal point would be understood to be one and the same, the magnitude of the azimuthal velocity of this combined, or unified, EMO, at any such point, would simply be the scalar sum of the two azimuthal velocities of the two original EMOs, as real (possibly negative) numbers.
Given the \(\frac{\pi }{2} \) phase difference between EMOs (1) and (2) we get that the unified azimuthal velocity is
where \(r \approx r_1 \approx r_2 \).
So the unified EMO has angular amplitude \(\sqrt{2} \varepsilon \), but apart from that, it can be thought of as an ordinary EMO. The only dependence on \(d \) is in the assumption \(r_1 \gg d,r_2 \gg d \).
We now need to identify the effective focal point of the unified EMO so that we can solve the motion of the entire unified system. The focal point of an EMO is the point where the azimuthal velocity is always zero. So it seems reasonable to demand that the definition of the effective focal point guarantee that a test particle positioned at the effective focal point should remain there. This implies that, given the definition of the effective focal point at some \(t_0\), which we denote by \( p(t_0 ) \), the focal point \(p(t) \) would be defined as a path in the body plane, determined by the action of the body EMOs at \(p(t) \) and the motion of the body focal points (I’m using a rather loose notation here, but we will eventually write the vector \({\dot{\varvec{p}}}(t)\) as a function of \(\hat{m}(t),\hat{n}(t)\)).
We must consider what we intend to use the effective focal point for. As described in the introduction, we will soon add two more EMOs perpendicular to the body plane which we shall call wheels, and these will serve to rotate the body plane around axes contained in it. Obviously the planes of the wheels would have to be positioned in such a way that they can act on body focal points (1) and (2). For the entire structure to be stable we will have to make sure that the movement of the body plane is in its turn communicated back to the wheels. This suggests the idea of positioning the wheel focal points at the body’s effective focal point.
From all this it is becoming clear that the effective focal point should be in some sense at rest in relation to the structure of the body plane. We make this more specific by stipulating that the effective focal point be at rest in relation to the basis \({\hat{m}},{\hat{n}} \). Seemingly, any point on the segment between focal points (1) and (2) would satisfy our stipulations: Imagine, for example, that we choose the middle of that segment to be the focal point. Since this segment lies on the half lines of EMOs (1) and (2) whose interaction determines \({\hat{m}} \) and \({\hat{n}} \), it is guaranteed that a test particle positioned at the middle of the segment will remain at the middle of the segment.
There is however a major drawback there. We will soon want to stipulate that the plane of a wheel acting on a body focal point be orthogonal to the body plane, so that the direction of the velocity that the wheel generates at the body focal point would always be orthogonal to the direction of the momentary motion of the affected focal point on the body plane. But positioning the wheel focal points on the segment between (1) and (2) would require both wheels to intersect the body plane along this segment. If we add the stipulation that the wheel planes be orthogonal to the body plane we end up with only one wheel plane. How much more flexible the system would be if we have two independent wheels, each acting on only one of the body focal points!
This leads to the idea of defining \(p(t_0)\) by raising a \(\frac{d}{2} \) long normal from the middle of the segment between focal points (1) and (2). That implies defining \(p(t_0)\) as the vertex opposite the hypotenuse in an isosceles right triangle where the hypotenuse is the segment between the focal points. Such a construction may enable us to position the two wheels on planes orthogonal to the body plane and to each other, intersecting the body planes along the lines determined by the segments between \(p(t_0)\) and focal points (1) and (2) respectively. There are two ways of constructing this, depending on the direction of the normal. The question is whether any of these constructions satisfies our first stipulation, namely, that a test particle positioned at the end of the normal at \(t_0 \) will remain at the end of the normal at any \(t \).
I propose that one of these constructions does satisfy the stipulation, but only at the limit \(\varepsilon \rightarrow 0 \) . This implies that for \(\varepsilon \ll \frac{\pi }{4} \) it satisfies the stipulation up to some small imprecision. We will start by defining the effective focal point to be the (only) intersection of two radial half lines of EMOs (1) and (2) that have equal phases. We’ll see how this definition unambiguously determines a point on the momentary body plane, and how, at the limit \(\varepsilon \rightarrow 0 \), this point turns out to be at the end of a \(\frac{d}{2} \) long normal from the middle of the segment between focal points (1) and (2). We will define a path p(\(t\)) by separately raising the normal at each \(t \), and then, identifying the point p(\(t_{0}\)) with the intersection of radial half lines with equal phases (assuming \(\varepsilon \ll \frac{\pi }{4}) \), we will try to show that a test object positioned at p(\(t_{0}\)) at \(t_0 \) would really follow the path p(\(t\)). This is not without problems and there are still important open questions.
Given the body plane as defined (the first of our four possibilities) we can assume that focal point (2) is on the \(\varphi =0\) half line of EMO (1) and focal point (1) is on the \(\varphi =\pi \) half line of EMO (2), and that the phase of EMO (2) is ahead by \(\frac{\pi }{2}\). Here I am using \(\varphi \) as an index for half lines, which is a little ambiguous. What I mean is that from EMO (1)’s point of view focal point (2) is on the half line that would oscillate round \(\varphi =0\) if there were no EMO (2), and from EMO (2)’s point of view focal point (1) is on the half line that would oscillate round \(\varphi =\pi \) if there were no EMO (1).
It follows that the equal phase point is at the intersection of the \(\varphi = \frac{\pi }{4} \) half line of EMO (1) with the \(\varphi = \frac{3\pi }{4} \) half line of EMO (2), because this satisfies \(\varphi _1 - (\omega t - \frac{\pi }{2}) = \varphi _2 - \omega t \), where \(\varphi _1 = \frac{\pi }{4} \) and \(\varphi _2 = \frac{3\pi }{4}\). Assuming \(\varepsilon \ll \frac{\pi }{4} \) we neglect the \(\approx \varepsilon \) deviation of each \(\varphi \) half line from its \(\varphi _0 \) position on the background plane, and get that the intersection lies approximately at the end of a \(\frac{d}{2} \) long normal from the middle of the segment between the focal points.
If we now replace the right-handed EMOs with left handed ones, the two half lines are
Satisfying
If we stick with right-handed EMOs but reverse the order of the phases we get
Satisfying
So in both cases the triangle is reflected through the hypotenuse. In the forth case, of left-handed EMOs with reversed phase order, we get the original triangle, with:
By defining p(\(t\)) as the point at the end of a \(\frac{d}{2} \) long normal raised from the middle of the segment between focal points (1) and (2) we immediately get that when the body focal points are translated infinitesimally by \(\varepsilon \omega d\cos (\omega t)\mathrm{d}t\) and \(\varepsilon \omega d\sin (\omega t)\mathrm{d}t\) in the direction parallel to \({\hat{m}} \), p(\(t\)) is translated by \(\frac{\varepsilon \omega d}{\sqrt{2} }\sqrt{\sin ^2(\omega t) + \cos ^2(\omega t)}\mathrm{d}t=\frac{\varepsilon \omega d}{\sqrt{2} }\mathrm{d}t\). It follows that unlike the equations of motion for the body focal points, the equation of motion for p(\(t\)) is regular at all \(t\), and p(\(t\)) moves with constant motion along a differentiable curve. By the definition of p(\(t\)) we have:
And using the equations of motion for \(\left( {{\begin{array}{*{20}c} {{\dot{x}}_ + } \\ {{\dot{y}}_ + } \\ \end{array} }} \right) \) and \(\left( {{\begin{array}{*{20}c} {{\dot{x}}_\_ } \\ {{\dot{y}}_\_ } \\ \end{array} }} \right) \) we get:
We could now in principal write the solution for \(\dot{\varvec{p}}(t)\) by substituting the expressions for \({\hat{m}},{\hat{n}}\) as functions of \(t\). But as a matter of fact, it is this form of the differential equation, giving \(\dot{\varvec{p}}(t)\) in terms of the momentary \({\hat{m}},{\hat{n}}\) basis, which will prove the most useful. It evokes a mental picture in which we forcefully keep \({\hat{m}},{\hat{n}}\) and p(\(t\)) in their place, and ask at each moment separately what would \(\dot{\varvec{p}}(t)\) be if we let go, and the answer we get is a vector of constant magnitude \(\frac{1}{\sqrt{2} }\varepsilon \omega d \) rotating with angular velocity \(\omega \) on the body plane.
Let us now confront the essential question of p(\(t\))’s suitability as a definition of the effective focal point, that is, try to find out if a test particle positioned at p(\(t\)) remains at p(\(t\)). We assume that a test particle is placed at p(\(t\)) at some general moment and try to calculate its momentary velocity. The calculation is based on the identification of p(\(t\)) with the point of equal phases.
We start by calculating the contribution of EMO (1) to the velocity at p(\(t\)). There are two terms, with coefficients that need clarifying:
The first term represents the contribution of the azimuthal velocity of EMO (1) at p(\(t\)), and the second term represents the contribution of the velocity of focal point (1), that is, the azimuthal velocity of EMO (2) at focal point (1). The \(\frac{1}{2} \) factor before the second term represents the fact that we are not working in the rest frame of focal point (2) but in a frame symmetric in regard to focal points (1) and (2), as we previously saw when discussing the equation for \(\left( {{\begin{array}{*{20}c} \dot{{\bar{x}}} \\ \dot{\bar{y}} \\ \end{array} }} \right) \).
The factor \(\frac{1}{\sqrt{2} } \) before the first term is more problematic, and the fact that I do not fully understand it is one of the more troubling points in my entire argument. The idea is a generalization of the argument in the previous paragraph concerning a point of view which has to be symmetrical in regard to focal points (1) and (2). We are interested in the infinitesimal translation caused at p(\(t\)) by the azimuthal velocity of EMO (1), but we consider it not in the rest frame of focal point (1) but in a frame symmetrical in regard to both focal points. Let \(G \) be the middle of the segment between the focal points, and think of a general point \(H \) on the normal raised from \(G \). In our case the distance \(|{GH}|\) is \(\frac{d}{2} \), but let’s think first of the limits \(|{GH}|\rightarrow \infty \) and \(|{GH}|\rightarrow 0 \). We are thinking of the infinitesimal translation caused by EMO (1) at \(H\) and are trying to find the ratio between this translation as seen in the rest frame of \(G\) and the translation as seen in the rest frame of focal point (1).
At the limit \(|{GH}|\rightarrow \infty \) the ratio must be 1, because the velocity of \(G\) in focal point (1)’s rest frame is negligible when compared with the azimuthal velocity generated by EMO (1) at \(H\). At the limit \(|{GH}|\rightarrow 0 \) the ratio is 0, because \(H \) becomes identified with G. If we put forward the conjecture that the ratio is \(\sin \delta \), where \(\delta \) is the base angle of the isosceles triangle whose base is the segment between focal points (1) and (2) and whose vertex is \(H \), we get the ratio \(\frac{1}{\sqrt{2}}\) for the case \(|{GH}|=\frac{d}{2}\).
By similar considerations, the contribution of EMO (2) is:
(where the sign of \(\frac{({\hat{n}} - {\hat{m}})}{\sqrt{2} } \) is derived by considering the positive direction of \(\varphi )\).
We sum the contributions to get:
This is equal to \({\dot{\varvec{p}}}(t) \) as calculated by raising the normal, and it follows that a test particle placed at p(\(t\)) remains at p(\(t\)). This result depends of course on the identification of the point of equal phases with p(\(t\)), and on the as yet questionable \(\frac{1}{\sqrt{2} } \) factor.
Let’s repeat the calculation for the other three possible states of the EMO combination. First let’s reverse the handedness. EMO (1)’s contribution is then
and EMO (2)’s contribution is
Summing the two contributions we get:
which is equivalent to reversing the direction of the normal in our original construction for p(\(t\)).
Taking the original handedness with reversed phase order we get that EMO (1)’s contribution is
and EMO (2)’s is
and summing we get
In this case the final result is identical to our original results but the contributions of the two EMOs have interchanged.
In the fourth case, with reversed handedness and order of phases, we get that EMO (1) contributes
and EMO (2) contributes
and the summation gives
which is identical to the second state but with interchanged contributions.
Figure 3 is the simulation from Fig. 1, with p(\(t\)).
The lower half of every “circle” represents a domain where the equation for \(\left( {{\begin{array}{*{20}c} {{\dot{x}}_ - } \\ {{\dot{y}}_ - } \\ \end{array} }} \right) \) is regular. By reversing the handedness we reverse the direction of rotation of p(\(t\)) (anticlockwise–clockwise) and the direction of the drift (right–left). Reversing the phase order reverses the drift direction but does not reverse the rotation. Reversing both the handedness and the phase order reverses the rotation without reversing the drift.
Taking \(\varepsilon \) 10 times smaller we get Fig. 4, where we see that the drift becomes negligible as \(\varepsilon \) grows smaller.
Let us now define the wheels of the EMO combination. We place the focal points of the two wheels at p(\(t\)) and the wheel planes orthogonally to the body plane and to each other, wheel (1) intersecting the body plane along the line through p(\(t\)) and focal point (1), and wheel (2) intersecting the body plane along the line through p(\(t\)) and focal point (2). By choosing p(\(t\)) for the wheel focal points, we assure that any translations of the body plane in any direction on the body plane be transferred to the wheels. The action of wheel (1) must be to translate focal point (1) in the direction perpendicular to the body plane, and the action of wheel (2) must be to translate focal point (2) in the direction perpendicular to the body plane. Determining what actually happens to the body plane at a given moment would depend on the momentary azimuthal velocity of wheel (1) at focal point (1), the momentary azimuthal velocity of wheel (2) at focal point (2), and the momentary direction of \({\dot{\varvec{p}}}(t) \), as we shall soon see.
Assume the first of the four body states. Without the wheels we have \({\dot{\varvec{p}}}(t) = \frac{1}{2}\varepsilon \omega d[ ( - \sin (\omega t)({\hat{m}} - {\hat{n}}) +\cos (\omega t)({\hat{m}} + {\hat{n}}) ] \). Note that \(\frac{{\hat{m}} + {\hat{n}}}{\sqrt{2} } \) is perpendicular to the plane of wheel (1), and the magnitude of the projection of \({\dot{\varvec{p}}}(t) \) on \(\frac{{\hat{m}} + {\hat{n}}}{\sqrt{2} } \) is proportional to \(\cos (\omega t) \). We now fix the phase of wheel (1) so that the azimuthal velocity generated by wheel (1) at focal point (1) be proportional to \(\cos (\omega t) \). Similarly, we fix the phase of wheel (2) so that its azimuthal velocity at focal point (2) be proportional to \(\sin (\omega t) \). We can add a \(\pi \) phase to both wheels, thus reversing the direction of the velocities they generate at focal points (1) and (2) respectively. This constitutes a third binary parameter of the 4-EMO combination.
Let’s assume that adding the wheels does not change the dynamics of the body plane, and specifically, that \({\dot{\varvec{p}}}(t) \) doesn’t change, and check whether this leads to any contradictions. We note that at \(\omega t = 0,\pi \) the motion of the effective focal point is momentarily equivalent to a rotation with angular velocity \(\varepsilon \omega \) round an axis perpendicular to the body plane and intersecting it at focal point (1), with the direction of rotation reversed between \(\omega t = 0 \) and \(\omega t = \pi \). At \(\omega t = \frac{\pi }{2},\frac{3\pi }{2} \) the motion is momentarily equivalent to a rotation with angular velocity \(\varepsilon \omega \) round an axis perpendicular to the body plane and intersecting it at focal point (2), with the direction of rotation reversed between \(\omega t = \frac{\pi }{2} \) and \(\omega t = \frac{3\pi }{2} \). In fact, at any \(t \) the motion of the effective focal point is momentarily equivalent to a rotation with angular velocity \(\varepsilon \omega \) round an axis perpendicular to the body plane and intersecting it at a point \(q(t) \), \(\frac{d}{\sqrt{2} } \) away from the effective focal point. In the rest frame of \(\hat{m}, \hat{n}\), \(q(t) \) moves in a circle round the effective focal point, with angular velocity \(\omega \). For example, if at \(\omega t = 0\, q(t) \) is at focal point (1), then at \(\omega t = \pi \) it is antipodal to focal point (1) on the \(q(t) \) circle.
The momentary rotation round \(q(t) \) determines a momentary motion of the wheel planes. This can be interpreted, in accordance with what we did when discussing the transformation rule of moving EMOs, as a combination of a momentary linear velocity of the wheel focal point and a momentary rotation of the wheel plane. For example, when \(q(t) \) is at focal point (1), the focal point of wheel (1) has a momentary velocity perpendicular to the wheel plane, and in addition, the wheel plane is rotating with angular velocity \(\varepsilon \omega \) round an axis contained in the wheel plane and passing through the wheel focal point. At the same moment, the focal point of wheel (2) is moving with linear velocity parallel to the wheel plane and the plane of wheel (2) is rotating with angular velocity \(\varepsilon \omega \) round an axis contained in the wheel plane and passing through the wheel focal point. In fact, at any \(t\) both wheel planes are rotating with angular velocity \(\varepsilon \omega \) round axes contained in them. So, according to our transformation rule, the angular velocities generated by the wheels have to be multiplied by the factor
We conclude that the motion of the effective focal point neutralizes the wheels so that they have no effect on the body plane. But is this the only self consistent solution? From our transformation rule we have that if we decrease the angular velocity of the rotation of the wheel planes the wheels awake, possibly causing a rotation of the entire body plane, which, in turn, may account for the decrease in the angular velocity of the rotation of the wheel planes. Let’s see this.
We shall now understand the term \({\dot{\varvec{p}}}(t) \) to signify the projection of the effective focal point’s velocity on the body plane.
We assume
with \(0 \leqslant \beta < 1\).
And check for self consistency.
The transformation factor now is
Therefore, the azimuthal velocity of wheel (1) at focal point (1) is
And the azimuthal velocity of wheel (2) at focal point (2) is
When the two wheels endow the two body focal points with equal velocities, that is when \(\sin (\omega t) = \cos (\omega t) \), the result is a momentary rotation of the entire body plane round an axis parallel to \({\hat{n}} \) and passing through the effective focal point. The angular velocity is
Here the numerator is the azimuthal velocity of each of the wheels, and the denominator is the distance between each of the body focal points and the axis of rotation.
When the two wheels endow the two body focal points with equal velocities in opposite directions, that is when \(\sin (\omega t) = - \cos (\omega t) \), the result is a momentary rotation round \({\hat{m}} \), with angular velocity \(\beta \varepsilon \omega \), calculated in the same manner as above.
When only one wheel is active, that is when \(\sin (\omega t)=0 \) or \(\cos (\omega t) = 0 \), the body plane momentarily rotates round an axis parallel to \(\frac{({\hat{m}}\pm {\hat{n}})}{\sqrt{2} } \) and passing through the effective focal point. The angular velocity is
Here the denominator is the distance between focal point (1) and the axis parallel to \(\frac{({\hat{m}} + {\hat{n}})}{\sqrt{2} } \), or the distance between focal point (2) and the axis parallel to \(\frac{({\hat{m}} - {\hat{n}})}{\sqrt{2} } \).
At a general \(t \), the body plane momentarily rotates round the axis parallel to \(\cos (\omega t)\frac{({\hat{m}} + {\hat{n}})}{\sqrt{2} } + \sin (\omega t)\frac{({\hat{m}} - {\hat{n}})}{\sqrt{2} } \) and passing through the effective focal point. We see this by observing that the distance between this axis and focal point (1) is \(\frac{d}{\sqrt{2} }\left| {\cos (\omega t)} \right| \), and the distance between this axis and focal point (2) is \(\frac{d}{\sqrt{2} }|{\sin (\omega t)}|\). The fact that the distances are proportional to the azimuthal velocities of the wheels at focal points (1) and (2) respectively guarantees that both wheels can be said to generate the same angular velocity, so that the axis can indeed be thought of as an axis of momentary rotation: The angular velocity that wheel (1) causes is \(\frac{\beta \varepsilon \omega \frac{d}{\sqrt{2} }(\cos \omega t))}{\frac{d}{\sqrt{2} }\cos \omega t} = \beta \varepsilon \omega \) and the angular velocity that wheel (2) causes is \(\frac{\beta \varepsilon \omega \frac{d}{\sqrt{2} }(\sin \omega t))}{\frac{d}{\sqrt{2} }\sin \omega t} = \beta \varepsilon \omega \), so that the body plane can be said to momentarily rotate round the momentary axis parallel to \(\cos (\omega t)\frac{({\hat{m}} + {\hat{n}})}{\sqrt{2} } + \sin (\omega t)\frac{({\hat{m}} - {\hat{n}})}{\sqrt{2} } \) with angular velocity \(\beta \varepsilon \omega \).
We now have that at any \(t \) the body plane is rotating round an axis contained in it and passing through the effective focal point with angular velocity \(\beta \varepsilon \omega \). As in the discussion of the rotation of the wheel planes, this also implies that each of the body EMOs is rotating with angular velocity \(\beta \varepsilon \omega \) round an axis passing through its focal point. For example, at \(t = 0 \), the momentary axis is parallel \(\frac{({\hat{m}} + {\hat{n}})}{\sqrt{2} } \) and contains the effective focal point, so it also contains focal point (2), while, in regard to EMO (1), we can interpret the rotation in terms of a momentary linear velocity of focal point (1), perpendicular to the body plane, plus a momentary rotation of EMO (1)’s plane round an axis parallel to \(\frac{({\hat{m}} + {\hat{n}})}{\sqrt{2} } \) and passing through focal point (1).
We therefore apply the transformation rule to get a factor \(\sqrt{1 - \left( {\frac{\varepsilon \omega \beta }{\varepsilon \omega }} \right) ^2} = \sqrt{1 - \beta ^2} \) so that:
And we have confirmed the internal consistency for any \(0 \leqslant \beta < 1 \).
For curves in \(R^3 \), the torsion is the angular velocity of the rotation of the Frenet frame round the tangent. A curve with constant curvature and torsion is a helix, and we get that, in the same sense that we think of the effective focal point as moving in a circle in the case \(\beta = 0 \), we can think of it as moving along a helix with curvature \(\sqrt{1 - \beta ^2} \) and torsion \(\beta \), in the case \(\beta > 0 \).
We now ask what kind of interaction would change a 4-EMO combination with \(\beta = 0 \) into a combination with \(\beta > 0 \). Let’s assume that some external EMO’s plane lies momentarily on the plane of one of the wheels of a \(\beta = 0 \) combination, say wheel (2), with the external focal point on the line determined by focal point (2) and the effective focal point, so that the effective focal point is contained in the segment whose ends are focal point (2) and the external focal point. It follows that the effective focal point and focal point (2) are momentarily on the same half line of the external EMO. The azimuthal velocity of the external EMO at the effective focal point is \(\mathrm{E}\Omega (D)\sin (\Phi ) \), where \(\Omega \) is the phase angular velocity, E is the angular amplitude, \(D \) is the distance between the external EMO and the effective focal point, and \(\Phi \) is the momentary phase of the oscillation of the half line. It follows that the azimuthal velocity of the external EMO at focal point (2) is \(\mathrm{E}\Omega (D + \frac{d}{\sqrt{2} })\sin (\Phi ) \). So the external EMO endows focal point (2) with a \(\mathrm{E}\Omega \frac{d}{\sqrt{2} }\sin (\Phi ) \) velocity relative to the effective focal point, in a direction perpendicular to the body plane. Note that the external EMO does not act on the EMO combination in any other way. We need to assume that this lasts for some \(\Delta t \ll \frac{2\pi }{\omega } \), and I tend to think of this ideally as a momentary event, with \(\Delta t \rightarrow 0 \).
Let’s assume that the interaction with the external EMO takes place at one of the phases when only the wheel involved in the interaction is affecting the body plane, while the momentary azimuthal velocity of the other wheel at its respective body focal point is zero. Since only one wheel is involved in our considerations, and assuming \(\mathrm{E}\Omega \sin (\Phi ) < \varepsilon \omega \), we get that the interaction perfectly mimics the momentary behavior of a 4-EMO combination with \(\beta = \Delta \beta = \frac{\mathrm{E}\Omega \sin (\Phi )}{\varepsilon \omega } \) . It follows that the interaction changes the combination into a combination with \(\beta = \frac{\mathrm{E}\Omega \sin (\Phi )}{\varepsilon \omega } \).
We can explain this by the following chain of causes and effects:
-
1.
Wheel (2) endows focal point (2) with the momentary azimuthal velocity appropriate for the \(\beta = \frac{\mathrm{E}\Omega \sin (\Phi )}{\varepsilon \omega } \) state, and hence endows the body plane with a momentary angular velocity \(\beta \varepsilon \omega \) round the axis parallel to \(\frac{({\hat{m}} - {\hat{n}})}{\sqrt{2} } \) and passing through the effective focal point.
-
2.
Consequently, the azimuthal velocities of both body EMOs are diminished by a factor \(\sqrt{1 - \beta ^2} \) and \({\dot{\varvec{p}}}(t) \) is diminished by the same factor.
-
3.
The change in \({\dot{\varvec{p}}}(t) \) causes the wheels to awaken and make their contribution as expected in a \(\beta = \frac{\mathrm{E}\Omega \sin (\Phi )}{\varepsilon \omega } \) state.
Note that the various elements of the causal chain are in fact simultaneous, and that the entire reasoning depends on the assumption that the interaction happens at a phase when only wheel (2) is active. A similar interaction happening at a different phase would rotate the body plane round an axis parallel to \(\frac{({\hat{m}} - {\hat{n}})}{\sqrt{2} } \) at a phase where it is supposed to be rotating round a different axis, and the resulting dynamic would be different than that of a self consistent \(\beta \) state. It would require further analysis, which I have not done, to determine whether such an interaction would end with the combination stabilizing, but in any case there would be no reason to expect a simple connection like \(\Delta \beta = \frac{\mathrm{E}\Omega \sin (\Phi )}{\varepsilon \omega } \).
Similarly, the value of \(\beta \) may change as a result of some less structured interaction, for instance, if an external EMO momentarily shares a wheel plane but its focal point is not on the line determined by the effective focal point and the respective body focal point. In such a case too, there is no reason to expect a simple connection like \(\Delta \beta = \frac{\mathrm{E}\Omega \sin (\Phi )}{\varepsilon \omega } \). In principle we could get \(\Delta \beta = \frac{\mathrm{E}\Omega \sin (\Phi )}{\varepsilon \omega } \) by generalizing our interaction to a general phase and stipulating that two external EMOs be involved, interacting with the two wheels in a synchronized way, but the case seems too rare to consider.
It therefore seems that if we aim to identify a consistent system of relations between changes in \(\beta \) and the properties of external EMOs, the interactions in which the external EMO shares the plane of a wheel, and its focal point is on the line determined by the effective focal point and the body focal point, at the right phase, are especially interesting. We refer to these as type (ii) interactions. From the current discussion we have that these interactions can occur at the phases \(\frac{n\pi }{2} \), but we will later see a reason to be especially interested in the phases \(n\pi \).
Note that besides endowing the body focal point with a \(\mathrm{E}\Omega \frac{d}{\sqrt{2} }\sin (\Phi ) \) velocity relative to the effective focal point, the interaction also endows the entire EMO combination with a \(\mathrm{E}\Omega D\sin (\Phi ) \) velocity which is not encoded by \(\Delta \beta \). It follows that if we discuss the motion of an EMO combination in terms of the various values of \(\beta \) assigned to it at different \(t \) intervals, we must remember that, as long as we think of the interaction as lasting for \(\Delta t > 0 \), we get that some effectively random fluctuations in position may occur during these interactions.
If we stipulate \(\mathrm{E}\Omega = \varepsilon \omega \) we get \(0 \leqslant \frac{\mathrm{E}\Omega \sin (\Phi )}{\varepsilon \omega } \leqslant 1 \). If, in addition, the external EMO is in itself a part of a similar 4-EMO combination, we have \(0 \leqslant \mathrm{B}\frac{\mathrm{E}\Omega \sin (\Phi )}{\varepsilon \omega } \leqslant 1\), where \(0 \leqslant \mathrm{B} < 1 \) denotes the state of the external EMO combination. In this context it may be interesting to remember that the spectrum of electromagnetic radiation is quite tightly bounded by the electron Zitterbewegung frequency.
In the current paper we will be especially interested in the case where the external EMO is in itself the wheel of a second 4-EMO combination, with the effective focal points of both combinations and the two relevant body focal points all momentarily on the same line, and both objects in suitable phases. Note that in the moment of interaction the two effective focal points are moving along the line determined by them, and the two objects are momentarily rotating round that line as axis. Let’s first assume that the first object changes from \(\beta = 0 \) to \(\beta = \beta _0 > 0 \), and then let’s change a frame of reference so that it is the second object which begins with \(\beta = 0 \). This implies moving from a picture where the first object is moving in a circle round the second object, to a picture where the second object is moving in a circle round the first object. It follows that in the new reference frame the second object changes from \(\beta = 0 \) to \(\beta = \beta _0 > 0\), but the direction of the velocity endowed to its participating body focal point is reversed in comparison with the velocity endowed to the body focal point of the first object in the original reference frame.
5 The wandering EMO procedure and the Dirac equation
We think again of the \(\beta = 0\) combination with
We now define a procedure that will allow us to encode some important aspects of this picture by an \(S^2 \) curve. This procedure is based on our understanding of EMO space as representing \(R\times S^3 \), but it also introduces some new ideas.
Recall a discussion we had when checking the self consistency of the \(\beta = 0 \) state. We first observed that at \(\omega t = 0,\pi \) the motion of the effective focal point can be understood as a rotation round an axis perpendicular to the body plane and passing through focal point (1), and that the same is true at \(\omega t = 0,\pi \), with focal point (2) replacing (1). The angular velocity is \(\varepsilon \omega \). Then we generalized this and interpreted the motion of the focal point at any \(t \) as a rotation round an axis intersecting the body plane at a point \(q(t) \), and noticed that \(q(t) \) can be thought of as moving in a circle of radius \(\frac{d}{\sqrt{2}} \) round the effective focal point, with angular velocity \(\omega \).
Let’s add a small modification to this idea. Instead of a rotation with angular velocity \(\varepsilon \omega \) round an axis intersecting the plane at a point \(\frac{d}{\sqrt{2} } \) away from the effective focal point, let’s think of a rotation with angular velocity \(\omega \) round an axis intersecting the plane at a point only \(\frac{\varepsilon d}{\sqrt{2} } \) away from the effective focal point. So we shrink the \(q(t) \) circle to have a radius \(\frac{\varepsilon d}{\sqrt{2} } \), instead of \(\frac{d}{\sqrt{2} } \), and we get more symmetry in the sense that both angular velocities involved are \(\omega \). Also in the interest of symmetry, we stipulate \(\frac{\varepsilon d}{\sqrt{2} } = 1 \).
Now let’s think of a reference frame where the effective focal point is at rest at the origin of EMO space, and imagine an EMO, referred to as the wandering EMO, whose focal point is positioned at \(q(t) \) at all \(t \), with the effective focal point on a constant point on that EMO’s plane . We ignore here the oscillations generated by this new EMO as we are now only concerned with the transformations that it has to undergo in order to keep the effective focal point (the origin) on a constant point of its plane, while its focal point encircles the origin as required.
As in similar situations we have encountered, we interpret the motion of the focal point of the wandering EMO in terms of a momentary linear velocity and a momentary rotation of the EMO plane. So the momentary motion can be understood as comprising a momentary velocity in the direction of the tangent to the circle of radius \(\frac{\varepsilon d}{\sqrt{2} } \), and a rotation with angular speed \(\omega \) round an axis perpendicular to the EMO plane and intersecting it at the focal point. The direction of this rotation must be the same as the direction of rotation of the focal point round the origin: for example, if the focal point encircles the origin clockwise, then this movement would be interpreted momentarily as linear movement along the tangent plus a clockwise rotation of the EMO plane with angular velocity \(\omega \).
Now if we want to generate \({\dot{\varvec{p}}}(t) \) at the origin at a given \(t \), all we need to do is rotate the new EMO plane round an axis perpendicular to it and intersecting it at its focal point, with angular velocity \(\omega \). Again I point out that we are now thinking only in terms of the transformations that the wandering EMO undergoes. Note that the direction of rotation has to be opposite to the direction of the rotation implicit in the motion of the wandering EMO round the \(q(t) \) circle. Let’s see this: Think back of \(q(t) \) as we first defined it, in the context of the body plane as we positioned it when we wrote the equations of motion. Focal point (1) is at \(( - d / 2,0,0) \) and focal point (2) at \((d / 2,0,0) \). The effective focal point moves at \(\omega t = 0 \) along a line parallel to \(\frac{({\hat{m}} + {\hat{n}})}{\sqrt{2} } \), which is the anticlockwise tangent to a circle whose center is at focal point (1). But in order to implement \({\dot{\varvec{p}}}(t) \) at \(\omega t = \frac{\pi }{2} \) by an anticlockwise rotation, we need an axis of rotation intersecting the body plane at \((d / 2,d,0) \), which is the point antipodal to focal point (2) on the \(q(t) \) circle. In order to get there at \(\omega t = \frac{\pi }{2} \), \(q(t) \) must rotate clockwise.
Going back to the wandering EMO it is now clear that in order to generate \({\dot{\varvec{p}}}(t) \) momentarily at any given \(t \) its plane has to rotate with angular velocity \(\omega + \omega = 2\omega \) relative to the picture where \(q(t) \) is encircling the effective focal point but no velocity is generated at the effective focal point. Let’s now think of this in connection with our understanding of EMO space as representing \(R\times S^3\backslash ( - 1,0,0,0) \). We stipulated \(\frac{\varepsilon d}{\sqrt{2} } = 1 \). Now we assume that the wandering EMO’s focal point is encircling the origin along the unit circle representing a great circle on the \(x_3\), \(x_4 \) plane. At any given \(t \), we can generate \({\dot{\varvec{p}}}(t) \) at the origin by rotating the wandering EMO plane round an axis intersecting its plane at its focal point, which would endow the effective focal point, placed at the origin, a velocity directed along a radial half line starting at the origin. Such a velocity would represent a flow along a momentary great circle on a plane \(x_1,y\), where \(y \) is a direction on the plane \(x_3,x_4 \). If at \(\omega t = 0 \) this is a rotation on the \(x_1,x_3 \) plane, then at \(\omega t = \frac{\pi }{2} \) it’s a rotation on the \(x_1,x_4 \) plane. There seems to be implied a flow defined by a momentary flow with angular velocity \(2\omega \) on a great circle on the plane \(x_1,y\), where \(y \) itself is rotating with angular velocity \(\omega \) on the \(x_3,x_4\) plane. This implies the following curve, written in \(R^3 \) coordinates:
So that the momentary plane of the \(2\omega \) rotation is
We can think of this as a point particle rotating with angular velocity \(2\omega \) round the rim of a rigid disk placed on the \(x,\cos (\omega t)y + \sin (\omega t)z \) plane, so that the disk itself is rotating with angular velocity \(\omega \) round the \(x \) axis contained in it.
One may ask if there isn’t any phase difference between this curve and the picture we had in EMO space. We may perhaps find some confirmation that the phases are compatible, at least up to a \(n\frac{\pi }{2} \) difference, in the fact that our curve is divided in four at \(\omega t = n\frac{\pi }{2} \) by the points where it intersects itself, whereas the motion in EMO space is divided in four at \(\omega t = n\frac{\pi }{2} \) by those moments when \(q(t) \) is at one of the body focal points or at a point antipodal to one of the body focal points on the \(q(t) \) circle.
In the wandering EMO procedure, the fact that the body plane is made of two body EMOs has been suppressed. It turns out that in order to get the physical results we have to bring that fact back to the forefront of our discussion. Here the insufficiency of my understanding of the wandering EMO procedure tells: once again I find myself having to present the result that I need deus ex machina, and then try to make some sense of it.
We now need to replace our curve
With the curve
The points of this curve are of course the same as those of the previous curve, but let’s see what has changed. We cut the last curve in four:
-
A:
\(0 \leqslant \omega t < \frac{\pi }{2} \)
-
B:
\(\frac{\pi }{2} \leqslant \omega t < \pi \)
-
C:
\(\pi \leqslant \omega t < \frac{3\pi }{2} \)
-
D:
\(\frac{3\pi }{2} \leqslant \omega t < 2\pi \)
Note that we get C from A by reflection through the \(x\), \(y \) plane, D from A by reflection through the \(x,z \) plane, B from C by reflection through the \(x,z \) plane and B from D by reflection through the \(x,y \) plane. Our new curve is ABCD and the previous curve was ACBD.
It seems to me that what we did in order to get the new curve amounts to folding the \(q(t) \) circle along a diameter passing through one of the body focal point. Assuming for clarity that there is no phase difference between EMO space and the wandering EMO space, we fold along the diameter passing through focal point (2), so that focal point (1) and its antipode on the \(q(t) \) circle are identified. This creates a distinction between the way the two body focal points are represented in the curve, which we can see if we again consider the self intersections of the curve at \(\omega t = n\frac{\pi }{2} \). In EMO space, at \(\omega t = 0 \) the effective focal point’s momentary velocity points away from focal point (2) and at \(\omega t = \pi \) it points towards it; at \(\omega t = \frac{\pi }{2} \) it points away from focal point (1) and at \(\omega t = \frac{3\pi }{2} \) it points towards it. The first curve reenacts these relations by reversing the direction of the flow between \(\omega t = 0 \) and \(\omega t = \pi \) and once again between \(\omega t = \frac{\pi }{2} \) and \(\omega t = \frac{3\pi }{2} \). But folding the \(q(t) \) circle the way we did implies that though the direction of the flow should be reversed between \(\omega t = \frac{\pi }{2} \) and \(\omega t = \frac{3\pi }{2} \), it should not be reversed between \(\omega t = 0 \) and \(\omega t = \pi \), and that is in fact what’s happening in the second curve, so that the moments \(\omega t = 0 \) and \(\omega t = \pi \) are clearly identified as the moments when \({\dot{\varvec{p}}}(t) \) is tangent to the EMO (1) azimuthal direction. The moments \(\omega t = \frac{\pi }{2} \) and \(\omega t = \frac{3\pi }{2} \), when \({\dot{\varvec{p}}}(t) \) is tangent to EMO (2), are now at the two ends of the oscillation of the \(x,\cos (\omega t)y + \sin (\omega t)z \) “disk” round the \(x \) axis. This oscillation has now replaced what was, in the first curve, a rotation round the \(x \) axis.
So the moments when \({\dot{\varvec{p}}}(t) \) is tangent to EMO (2) now correspond to the two points at the ends of the diameter along which we have folded the \(q(t) \) circle, and as such, they have become in a sense discontinuities (though the second curve is continuous, just like the first, the “disk rotation” has been replaced with an oscillation). On the other hand, EMO (1) has now lost its antipode on the \(q(t) \) circle, so that whenever \({\dot{\varvec{p}}}(t) \) flows tangently to it, it flows in the same direction. I tend to interpret the folding of the \(q(t) \) circle as in some sense choosing to look at things from EMO (1)’s point of view. If this interpretation is in any way valid it might help to justify the most important consequence I would like to draw from the current discussion: From now on we will only consider those type (ii) interactions in which focal point (1) is involved, that is the \(\omega t = 0 \) and \(\omega t = \pi \) type (ii) interactions. This makes at least some sense because if the object we’re studying in the wandering EMO space is defined by EMO (1)’s perspective, then when a type (ii) interaction involving EMO (2) changes the value of \(\beta \), this should be perceived as resulting from EMO (1)’s interaction with wheel (1), rather than an interaction with an external object.
Let’s study the curve a bit. We differentiate and get, up to normalization, the tangent to the curve:
(The minus sign before the last term refers to \(0 \leqslant \omega t < \frac{\pi }{2},\frac{3\pi }{2} \leqslant \omega t < 2\pi \) and the plus sign to \(\frac{\pi }{2} \leqslant \omega t < \frac{3\pi }{2})\).
By differentiating only the functions of \(2\omega t \) we get an expression identical to the first two terms of the previous expression:
This is the flow on the momentary \(2\omega \) circle, which I will refer to as the \(2\omega \) flow. Note that at \(\omega t = \frac{n\pi }{2},n = 0,1,2,3 \), the tangent of the \(2\omega \) circle is the same as the tangent of the curve, since the third term of the first expression is zero.
To acquire some basic intuition regarding the \(2\omega \) flow, we notice that at \(t = 0 \) its direction is \(y \) and the circle is on the \(x\), \(y \) plane; at \(\omega t = \frac{\pi }{4} \) its direction is \(( - x) \) and the plane is \(x,\frac{1}{\sqrt{2} }(y + z) \); at \(\omega t = \frac{\pi }{2} \) the direction is \(( - z) \) and the plane is \(y\), \(z \); and so on. The directions of this flow at the moments \(\omega t = \frac{n\pi }{4},n = 0,1,2,\ldots ,8 \) are:
We now leave the \(2\omega \) flow and go back to the tangent field of the curve. Consider its projections on the planes \(x,y,y,z\) and \(x\), \(z \). The projection on \(x,z\) can be divided symmetrically into two parts, \(\omega t \in (0,\pi ) \) and \(\omega t \in (\pi ,2\pi ) \), with the direction of rotation on the \(x,z\) plane reversed in the second part compared to the first part. The projection on \(y,z\) can be divided in four quarters, with the direction of rotation reversing twice, at \(\omega t = \frac{\pi }{2} \) and \(\omega t = \frac{3\pi }{2} \). The accumulated angle of rotation along a cycle on either plane (\(x,z\) and \(y,z\)) is therefore zero. However, the case of the \(x,y\) plane is different: there is no reversal of the direction of rotation and the accumulated angle is \(4\pi \).
If we were to randomly pick an interval \(\Delta \omega t \ll \frac{\pi }{2} \) and look at the projections of the tangent field on the three orthogonal planes, in the case of the \(y,z\) and \(x,z\) projections we have equal probabilities for both directions of rotation, but the direction of rotation of the \(x,y\) projection is completely determined. This leads to the idea that our curve should play some role in the description of the spin \(z\) eigenstates of a spin half particle. Note that \(x,y\) is the plane of the \(2\omega \) rotation at \(\omega t = 0,\pi \), so there may be some special interest in studying the \(\omega t = 0,\pi \) moments. I have already mentioned in the introduction that the \(2\omega \) flow would have something to do with our understanding of the dynamic phase of physical particles, and we still need to see how these various ideas combine.
I do not completely understand the meaning of the next, crucial, step. The wandering EMO procedure has given us an \(S^2 \) curve and has also lead us to think of the continuum of planes \(\left\{ {x,\left| {\cos (\omega t)} \right| y + \sin (\omega t)z} \right\} \) in \(R^3 \), with a great circle on each of these planes corresponding to the momentary \(2\omega \) flow. Let us call \(R^3 \), in this context, the wandering EMO space. As we said, we can think of our curve as describing a point particle rotating with angular velocity \(2\omega \) round the rim of a rigid disk, which in itself is oscillating with angular velocity \(\omega \) round the \(x \) axis, that is, on the \(y,z\) plane. We will now identify the wandering EMO space, at each \(t \) separately, with EMO space, stipulating that the momentary \(x,|{\cos (\omega t)}|y + \sin (\omega t)z \) plane be identified with the body plane, and that the great circle on this plane be momentarily identified with the circle on the body plane which is momentarily evoked by the equation
This means that in spite of our reasoning when we discussed the wandering EMO procedure, we now in some sense identify the point particle rotating in the wandering EMO space as representing the effective focal point. A \(2 \) factor between the angular velocities is therefore implied, since the \(2\omega \) flow on the momentary \(x,|{\cos (\omega t)}|y + \sin (\omega t)z \) plane is to be understood, each moment separately, as representing the \(\omega \) flow on the body plane. Hence, we interpret the \(\omega \) oscillation of our imaginary disk on the \(y,z\) plane as in some sense representing an oscillation of the wandering EMO space relative to EMO space. This is a bit of an oversimplification, as we must keep in mind that the effective focal point does not really rotate in a circle on the body plane, but rather, the rotation we saw was a property of the \({\dot{\varvec{p}}}(t) \) differential equation. Note also that the wandering EMO space is defined by the specific EMO combination we are looking at, so that, obviously, different objects in EMO space will generally not agree on the oscillations of the wandering EMO space. This means that we have now actually added a hidden compact dimension to our theory.
Now considering the \(\beta > 0 \) case, the above identification allows us to resort to the same arguments we used in EMO space. From the factor \(2 \) in angular velocities it follows that in the case of \(\beta > 0 \), the momentary effect of the wheels is to rotate the entire picture of the wandering EMO space round the momentary tangent to the \(2\omega \) flow, with angular velocity \(2\omega \beta \), while the rotation on the momentary \(2\omega \) plane is slowed down to an angular velocity \(2\omega \sqrt{1-\beta ^2}\). So, considering only the momentary \(2\omega \) flow and the momentary effect of the wheels, we can imagine our point particle as moving along a momentarily defined helix with curvature \(\sqrt{1-\beta ^2}\) and torsion \(\beta \), identifying the momentary \(2\omega \) plane with the helix’s momentary osculating plane. This is of course only a momentary picture, because any interval \(\Delta t > 0 \) involves also the \(\omega \) oscillation, which we have suppressed in this description.
Let’s see this in a little more detail. With \(\beta = 0 \), the point particle would be, at \(\omega t = 0 \), at \((1,0,0) \). The \(2\omega \) plane would be \(x,y\), the direction of the velocity would be \(y\) and the derivative of the velocity, concentrating on the motion on the momentary \(2\omega \) circle and ignoring the oscillation on the \(y\), \(z \) plane, would be in the direction \( - x \). So the Frenet basis of the imagined momentary \(2\omega \) circle would be \({\varvec{t}}=\hat{y},{\varvec{n}} = - \hat{x},{\varvec{b}} = \hat{z} \). Taking the natural parameterization with \(\mathrm{d}s=2\omega \mathrm{d}t\) we have curvature \(\kappa = 1 \) and torsion \(\tau = 0 \). A helix with radius \( a \) and step \(2\pi b \) is given by \((a\cos l,a\sin l,bl) \) where the length element is \(\mathrm{d}s=\sqrt{a^2+b^2}\mathrm{d}l\), the curvature \(\frac{a}{a^2 + b^2} \) and the torsion \(\pm \frac{b}{a^2 + b^2} \). In the case of \(\beta > 0 \), we have \(l = 2\omega t \), \(\mathrm{d}s=\mathrm{d}l=2\omega \mathrm{d}t\), \( a = \sqrt{1 - \beta ^2} \), \( b = \beta \), \(\kappa = \sqrt{1 - \beta ^2} \) and \(\tau = \pm \beta \). The sign of the torsion depends on the binary parameter of the wheels, determining the direction of their rotation. Since our \(2\omega \) plane is the osculating plane, the helix axis is not perpendicular to the \(2\omega \) plane but rather has a \(\sin ^{ - 1}(\beta ) \) tilt.
Wanting to identify type (ii) interactions (or at least type (ii) interactions involving two similar EMO combination) as representing a particle interacting with a photon, we are lead to identify the direction of the line between our point particle and the external focal point at \(\omega t = 0 \) and \(\omega t = \pi \) as the momentary direction of the flow of physical time in our point particle’s view. (Note that the term “momentary”, is used here, as before, on the premise that \(t \) is identified as a metaphorical time. The same goes for any other time-related language, unless differently specified). In the \(\beta = 0 \) case this is \(y \), the direction of the tangent to the momentary \(2\omega \) circle. In the \(\beta > 0 \) case the direction of the flow of physical time is the tangent to the helix. Taking the most natural units for physical time, we have \(\mathrm{d}\mathrm{time}= \mathrm{d}s = 2\omega \mathrm{d}t = \sqrt{a^2 + b^2}\mathrm{d}l\). In the case of \(\beta > 0 \), the magnitude of the projection of the flow of physical time on the plane perpendicular to the helix axis is \(a\mathrm{d}l=\sqrt{1-\beta ^2}\mathrm{d}s\). But when \(\beta \rightarrow 0 \), the osculating plane (the \(2\omega \) plane) becomes identified with the plane perpendicular to the helix axis. Therefore, from the point of view of an EMO combination with \(\beta = 0 \), the flow of physical time of a \(\beta >0\) object is identified as the projection on the plane perpendicular to the helix axis. So we get that from the point of view of the \(\beta = 0 \) object, the flow of physical time of an EMO combination with \(\beta >0\) is slowed down by a factor of \(\sqrt{1 - \beta ^2} \).
Looking again at the \(\beta = 0 \) case, the direction of the momentary tangent is \(y \), and it follows that the direction of the photon wave vector must be \( + y \) or \( - y \). The photon is emitted at some time in the physical past but at the same \(t \), somewhere along the \(\{{(1,y,0)|{-\infty <y}<\infty }\}\) line. When we get to the Dirac equation we shall interpret the helix torsion in connection with physical momentum in the direction of the binormal, so that the interaction we are now discussing will be understood to endow the EMO combination with momentum in either the \( + z \) or the \( - z \) direction, depending on the direction of the rotation of the wheels. We will be concentrating on the \(\omega t = 0\) case for a while, thus initially limiting the discussion to momenta in the spin direction.
Let us go a little deeper into the question of the direction of the flow of physical time: Is it from \(y \) to \( - y \) or vice versa? In our definition and discussion of type (ii) interactions we understood them in terms of a rotation of the body plane round axes contained in it and passing through the effective focal point, so that the interaction rotates the body focal point involved in a circle round the effective focal point, and not the other way round. To get this we had to assume the external focal point to be on the half line starting at the body focal point and passing through the effective focal point. For the photon to have been emitted in the physical past we must understand physical time as flowing from the external focal point toward the EMO combination. It follows that physical time flows from the effective focal point toward the body focal point and never vice versa.
Now, in writing our curve in the wandering EMO space there has been some arbitrariness: I have not gone into the question of how exactly the curve would change if we changed the binary parameters of the body plane. Moreover, I have not gone in detail into, on the one hand, the question of rotating the EMO combination by angle \(\pi \) round axes passing through the effective focal point or reflecting it through planes passing through the effective focal point, and on the other hand, the question of rotating the wandering EMO curve by angle \(\pi \) round axes passing through the origin or reflecting it through planes passing through the origin.
Some of these questions will be soon addressed when we discuss spin and charge, but much remains to be clarified. I’m pointing this out now for the following reason: Because physical time always flows from the effective focal point toward the body focal point, and recalling the folding of the \(q(t) \) circle, we now seem to have that in the wandering EMO space physical time flows in the same direction at \(\omega t = 0 \) and \(\omega t = \pi \), which we can say is \( + y \), depending on a choice of convention. This means that the photon was emitted from a particle in the \( - y \) direction. To get an interaction with a photon emitted in the physical past in the opposite direction we could hopefully make another choice in EMO space, perhaps the one amounting to reflecting the wandering EMO curve through the \({\hat{x}},{\hat{z}} \) plane. More work is required in order to ascertain what would the suitable choice in EMO space be, but my point is just that, I hope, we have not lost the freedom to chose whether the photon arrives from \( + y \) or \( - y \).
The same type of consideration would possibly help to endow the current picture with some other seemingly missing degrees of freedom. For one, on the face of it there appears to be a dependence of the sign of the momentum endowed to the EMO combination, \(z \) or \( - z \), on the sign of direction of the photon spin (the direction of the rotation caused by the wheels?). This however may be solved by taking some other reflection in the wandering EMO space, maybe through the \(y,z\) plane. A more serious problem may be the fact that we are now only thinking of photons arriving from the \({\pm }y\) directions. I imagine that the first step toward getting freed from this constriction would be to explore the question of the \(\omega t = \frac{\pi }{2},\frac{3\pi }{2} \) type (ii) interactions, which I have not done.
Let’s get to the question of rotating the wandering EMO curve by \(\pi \). To keep things simple, we will always assume that the external EMO focal point is in the right direction to be involved in a legitimate type (ii) interaction. Since rotating the curve by \(\pi \) round the \(x \) or \(z \) axis reverses the direction of the \(\omega t = 0 \) tangent from \( + y \) to \( - y \) and vice versa, it is implied that when rotating the curve by \(\pi \) round the \(x \) or \(z \) axes we also change the direction of the external EMO accordingly.
As we have seen, the action of the wheels at \(\omega t = 0 \) is to rotate the curve round the tangent at \((1,0,0) \), which is parallel to the \(y \) axis. Imagine rotating our \(\beta = 0 \) curve through angle \(\pi \) round this axis. That is equivalent to a rotation through angle \(\pi \) round the \(y \) axis, plus a translation by \(2 \) in the positive direction of the \(x \) axis. In the following discussion we will try to describe the momentary rotation round the tangent as a process which aims to transform one object, our original curve, into another object, the curve rotated through angle \(\pi \). We want to study some intrinsic properties of these two objects, properties which are unaffected by translation. This will be easier to do if we identify the second curve with the curve we get by rotating through angle \(\pi \) round the \(y \) axis, ignoring the translation.
Let’s consider then the three curves we get by rotating our \(\beta = 0 \) curve through angle \(\pi \) round the axes \(x,y\) and \(z \) (passing through the origin). For each of these three curves let’s think of the moment \(\omega t = 0 \) and of the infinitisemal rotation round the tangent (not passing through the origin) generated by activating the wheels at \(\omega t = 0 \), and consider the properties of the imagined momentary helices associated with this infinitisemal rotation. Rotating the original curve through angle \(\pi \) round the \(y \) axis gives the new curve \(\cos (2\omega t){\hat{z}} + \sin (2\omega t)\left[ {\left| {\cos (\omega t)} \right| {\hat{y}} - \sin (\omega t){\hat{x}}} \right] \). In this new curve the point particle is at \(( - 1,0,0) \) at \(\omega t = 0 \), instead of \((1,0,0) \), and the tangent at \(( - 1,0,0) \) is parallel to \( + y \). Assuming, as before, that the wheels generate a momentary rotation round the tangent in the negative direction, the momentary helix flow gives the direction \( - z \) when projected on the axis perpendicular to the momentary \(2\omega \) plane, instead of \(z \). Rotating the original curve through angle \(\pi \) round the \(z \) axis also moves the point particle to \(( - 1,0,0) \), but it also reverses the direction of the tangent to \( - y \). Once again, the point particle being at \(( - 1,0,0) \) implies a reversal of the direction of the projection of the momentary helix flow on the axis perpendicular to the \(2\omega \) plane from \(z \) to \( - z \). In addition, the reversal of the direction of the tangent causes the reversal of the handedness of the momentary helix. Rotating the original curve through angle \(\pi \) round the \(x \) axis leaves the point particle at \((1,0,0) \), so there is no reversal of the direction of the projection of the momentary helix flow on the axis perpendicular to the \(2\omega \), which remains \(z \). But in this case the direction of the tangent is reversed, so that the handedness of the momentary helix is reversed too.
We have four \(\beta = 0 \) curves then, divided into two pairs by the position of the point particle at \(\omega t = 0 \) being \((1,0,0) \) or \(( - 1,0,0) \), each pair divided in two by the direction of the tangent being \(y \) or \( - y \), and these two binary degrees of freedom induce two binary degrees of freedom of the imaginary momentary helices describing the momentary motion in the \(\beta > 0\) case, namely, the direction of the projection of the flow on the axis perpendicular to the \(2\omega \) plane, and the handedness. Given one of the two directions of the projection of the flow on the axis perpendicular to the \(2\omega \) plane, say \(z \), reversing the handedness is equivalent to reversing the direction of the rotation on the \(2\omega \) plane. This leads to the idea of identifying the reversal of the projection of the flow on the axis perpendicular to the \(2\omega \) plane as the reversal of the electric charge, and identifying the reversal of the handedness as the reversal of the spin state, say from \( \uparrow _z \) to \( \downarrow _z \).
Let’s make sure the above argument still makes sense if we compare the spins of two particles with opposite charges. Think of the electron magnetic moment. Its sign is reversed if either the spin or the charge signs are reversed, and it is not reversed if both are reversed. In our picture, for the charge to be reversed we have to reverse the direction of the projection of the flow on the axis perpendicular to the \(2\omega \) plane; but this reverses the handedness too, unless we also reverse the direction of rotation on the \(2\omega \) plane. So in order to reverse only the charge, we need to reverse both the direction of the projection of the flow on the axis perpendicular to the \(2\omega \) plane and the direction of the rotation on the \(2\omega \) plane, so that the handedness is not reversed. When calculating the magnetic moment we then have a factor of \(( - 1)( - 1)^2 = - 1 \), as required, where the first \(( - 1) \) factor represents the reversal of the direction of the projection of the flow on the axis perpendicular to the \(2\omega \) plane, pertaining to charge, and the \(( - 1)^2 \) factor represents the fact that the handedness is not reversed, corresponding to the spin not being reversed. In order to reverse both charge and spin we need to reverse only the direction of the projection of the flow on the axis perpendicular to the \(2\omega \) plane, so that the handedness too is reversed, and in the magnetic moment we get a factor of \(( - 1)(-1)=1\), as required, where the first \(( - 1) \) represents the reversal of the direction of the projection of the flow on the axis perpendicular to the \(2\omega \) plane, pertaining to charge, and the second represents the reversal of the handedness, pertaining to spin.
We can see some initial confirmation of the idea that rotating the curve through angle \(\pi \) round the \(y \) axis reverses the electrical charge (the \(C \) transformation) in the following observation: reflecting the curve through the \(x,z\) plane so that \(y\) is reversed to become \( - y \) constitutes a reversal of the direction of physical time (the \(T \) transformation), and indeed, if we rotate the curve through angle \(\pi \) and then reflect the curve through the \(x,z\) plane, we get \(x \rightarrow - x\), \(y \rightarrow - y\), \(z \rightarrow - z\) (the \(P\) transformation), hence \(\hbox {CPT}=\hbox {Identity}\).
Let’s write the second Frenet equation for the momentary helix at \(\omega t = 0 \):
And substitute the curvature and torsion:
We make a change of variables
(which means that we take the laboratory time, not the particle’s proper time).
And we get:
Note that the change of variables from \(t \) to physical time removed the dependence of the curvature on \(\beta \).
We now define a new notation. At first we restrict our discussion to the \(\beta = 0 \) case, and the general idea is to identify the momentary \(2\omega \) circle with the unit circle in the complex plane, separately for each value of \(t \). In fact, our conventions force us to add a minus sign, reversing the direction of rotation round the \(2\omega \) circle by reflecting the complex plane through the real axis: for example, at \(\omega t = 0 \), the \(2\omega \) circle is the unit circle in the \(x,y\) plane, and we now define the unit circle in the complex plane to be the unit circle in the \(x, - y \) plane, so that the point \((1,0,0) \) is the complex 1 and the point \((0, - 1,0) \) is \( i \). At \(\omega t = \frac{\pi }{2} \), we then have \((1,0,0) \) as the complex 1 and \((0,0, - 1) \) as \(i \).
With \(\beta = 0 \) we have
Which can now be written as
where \(\psi \equiv \varvec{n}\) is a complex function and the equation simply represents the momentary rotation round the momentary complex unit circle. Since we define this formalism separately for each \(t\), we have \(\psi \equiv \varvec{n} \) and \(\frac{\mathrm{d}\psi }{\mathrm{d}\mathrm{time}}=- i\psi \) for any value of \(t \).
We now want to move on to the case \(\beta > 0 \). In that case we have a non-zero torsion term in the second Frenet equation, which means that beside the momentary rotation round the momentary \(2\omega \) circle, we have a momentary rotation of the \(2\omega \) circle round the tangent \(\varvec{t} \) as axis. In order to allow our complex formalism to deal with that, we first have to define new coordinates to denote rotations in \(R^3 \), as follows: A rotation by angle \(\theta \leqslant \pi \) in the negative direction round an axis \( a{\hat{x}} + b{\hat{y}} + c{\hat{z}} \) (with \( a^2 + b^2 + c^2 = 1) \) is denoted by 4 real amplitudes \(\psi ^R_1,\psi ^R_2,\psi ^R_3,\psi ^R_4 \) satisfying \((\psi ^R_1 )^2 + (\psi ^R_2 )^2 + (\psi ^R_3 )^2 + (\psi ^R_4 )^2 = 1 \) where \(\psi ^R_1 = \cos \frac{\theta }{2} \), \(\psi ^R_2 = a\sin \frac{\theta }{2} \), \(\psi ^R_3 = b\sin \frac{\theta }{2} \) and \(\psi ^R_4 = c\sin \frac{\theta }{2} \). For example, a rotation through angle \(\theta < \pi \) in the negative direction round the \(y \) axis \((a = 0,b = 1,c = 0) \) is denoted by \(\psi ^R_1 = \cos \frac{\theta }{2} \), \(\psi ^R_3 = \sin \frac{\theta }{2} \) and \(\psi ^R_i = 0,i = 2,4 \), while a rotation through angle \(\theta \leqslant \pi \) in the positive direction round \(y \) is a rotation in the negative direction round \( - y (a = 0,b = - 1,c = 0) \) and is therefore denoted by \(\psi ^R_1 = \cos \frac{\theta }{2} = \cos \frac{ - \theta }{2} \), \(\psi ^R_3 = - \sin \frac{\theta }{2} = \sin \frac{ - \theta }{2} \) and \(\psi ^R_i = 0,i = 2,4 \).
Our complex formalism allows us to express the angular velocity of the rotation of the Frenet frame round the binormal (as axis), namely, the curvature, in terms of the rate of change of the phase of the complex function \(\psi \). We would now like to be able to express the angular velocity of the rotation of the Frenet frame round the tangent, namely, the torsion, in terms of the rate of change of the magnitude of \(\psi \), or, more exactly, the rates of change of the magnitudes of four complex functions \(\psi _{1}, \psi _{2},\psi _{3},\psi _4 \) satisfying \(|{\psi _1}|^2 +|{\psi _2}|^2 + |{\psi _3}|^2+|{\psi _4}|^2=1\). As stated before, our complex formalism is defined separately for each \(t \): So, unifying our definition of the complex unit circle at any specific \(t \) with our new formalism for rotations in \(R^3 \), we get coordinates for a \(R^3\times S^1 \) structure, where we have the complex unit circle as previously defined together with all the circles we get by rotating it. I once again stress that this is defined separately for each \(t\). We also need to add phase differences between the non-rotated complex unit circle and the rotated ones, so that a rotation through angle \(\frac{\theta }{2} \) would dictate a phase difference of \(\theta \). For example, the non-rotated complex unit circle, which at \(\omega t = 0 \) is in the \(x, - y \) plane, is denoted by \(|{\psi _1}|=1,|{\psi _{2,3,4}}|=0 \). Since we have chosen the point \((1,0,0) \) to be the complex 1, that is, have phase (argument) 0, we might expect the point denoted by \(|{\psi _1}|=\frac{\sqrt{2} }{2},|{\psi _2}|=\frac{\sqrt{2} }{2},|{\psi _{3,4}}| = 0 \) and phase \(0\) to be the point \((1,0,0) \) in the unit circle in the \(x, - z \) plane. But, having added a phase difference of \(2*\frac{\pi }{2} \) this turns out be the point \(( - 1,0,0) \) in the unit circle in the \(x, - z \) plane, instead.
The idea of this last definition is that if we now let the point particle rotate through an infinitesimal angle \(\sqrt{1 - \beta ^2} d2\omega t \) on the momentary \(2\omega \) plane, while letting the momentary \(2\omega \) plane rotate (under the action of the wheels) through an infinitesimal angle \(\beta d2\omega t \), the overall phase that the particle passes on the momentary helix is \(d2\omega t\), so that we can think of the particle as rotating round the complex plane with angular velocity \(2\omega t \), just like in the \(\beta = 0 \) case.
We can now go back to the second Frenet equation with non-zero torsion, which, after the change of variables, was:
This is of course a vector equation, while the Dirac equation is a complex scalar equation on a fiber bundle, with the fiber, a copy of the complex plane, defined at every spacetime point. But note that our understanding of the complex formalism and of physical time must lead us to reinterpret Dirac’s equation as a vector equation, since, on the one hand, we momentarily identify the complex plane with a specific plane in the wondering EMO space, and on the other hand, we momentarily identify the flow of physical time with a specific direction, and therefore, a derivative by physical time is in fact a directional derivative in the wandering EMO space.
The torsion term represents the angular velocity of the rotation of the osculating plane round the tangent. If that were the only rotation taking place, that is, if we ignore the rotation on the \(2\omega \) plane, then the momentary tangent would be in the \({\pm }z\) direction (the sign depending on the direction of the rotation of the wheels), and our abstract point particle would be infinitesimally translated in that direction, relative to the center of the momentary \(2\omega \) circle. This leads to the idea of associating the torsion with the \({\pm }z\) momentum term, which works well with the magnitude of the torsion term being \({\pm }\frac{\beta }{\sqrt{1 - \beta ^2} } \). We are therefore aiming at a picture where the \(\frac{\beta }{\sqrt{1 - \beta ^2} }\varvec{b}(s) \) term would be understood as equivalent to the \(\frac{\partial \psi _3 }{\partial z}{\hat{z}} \) term in Dirac’s equation. We have \(\frac{\left| {\partial \psi _3 } \right| }{\partial t} = 2*2\omega \beta \), where I added the extra factor of 2 because a rotation through \(\pi \) rather than \(2\pi \) is required in order to change \(|{\psi _3}|\) from 0 to 1. But I think there’s no problem in assuming that this 2 factor is hidden in the ratio of time units and distance units. The factor of \(\frac{1}{\sqrt{1 - \beta ^2} } \) which is needed in order to have \(\frac{|{\partial \psi _3}|}{\partial z} \propto \frac{\beta }{\sqrt{1 - \beta ^2} } \) comes, I think, from physical length contraction, following physical time dilation through the same considerations as in special relativity. So, using our complex formalism with the right units, we now have:
which is our vector interpretation of the Dirac equation as a deterministic equation of motion in the case of a free particle in a spin \(z \) eigenstate \( \uparrow _z \) and with momentum \(\frac{\beta }{\sqrt{1 - \beta ^2} }{\hat{z}} \).
We already noted that the change of variables from \(t \) to physical time removed the dependence of the curvature on \(\beta \). We have now associated the curvature term with the mass term in the Dirac equation. I will later briefly discuss the possibility that more complicated EMO combinations could have a role in describing hadrons, similar to the role that our 4-EMO combination may have in describing the electron. In the case of such combinations, the motion of the effective focal point is expected to be more complicated and not restricted to one plane. At this point it is mere speculation, but imagine the effective focal point moving, in the case \(\beta = 0 \), along a complicated curve made of many little curls, where the effect of the wheels is to rotate some plane momentarily identified as the plane of the momentary curl, in a way analogous to the way the wheels rotate the body plane in our current case. The momentum endowed to the particle by the wheel-generated rotation may turn out to be proportional to the radius of a typical curl. So this might lead to the idea of mass being proportional to the curvature of the effective focal point’s curve. We will briefly refer to this point when we discuss hadrons and again when we discuss gravity.
We still need to deal with momentum in directions other than the spin direction. Let’s repeat the same discussion we had for \(\omega t = 0 \), this time with \(\omega t = \frac{\pi }{2} \). The momentary \(2\omega \) plane is \(x,z\), and the wheels generate a rotation round the tangent \( - z \). The point particle is at \(( - 1,0,0) \) and is therefore endowed momentum in the \( + y \) direction if the wheels generate a rotation of the \(x,z\) plane round the \(z \) axis in the negative direction. Our discussion of the reversal of the electric charge, which was limited to \(\omega t = 0 \), is still valid, because once again, a rotation through \(\pi \) round either \(z \) or \(y \) would reverse the momentary position from \(( - 1,0,0) \) to \((1,0,0) \) and would therefore reverse the direction of the momentum from \( + y \) to \( - y \), while a rotation round \(x \) would not reverse the momentum. On the other hand, the question of the reversal of the handedness of helices with axes along the \(y \) direction is immaterial to us, because we are dealing with spin \(z \) eigenstates.
So what we get is that in order to generate \(y \) momentum we need a rotation working to reverse both spin and charge, while for \(z \) momentum we only needed charge reversal. It seems then that my basis in \(R^3 \) is rotated by \(\frac{\pi }{2} \) round the \(z \) axis relative to the usual Dirac notation, so that the \( + y \) momentum generated at \(\omega t = \frac{\pi }{2} \) according to my notation is in fact \( + x \) momentum using the usual notation. So, using my notation, we have:
which is our vector interpretation of the Dirac equation as a deterministic equation of motion in the case of a free particle in a spin \(z \) eigenstate \( \uparrow _z \) and with the momentum in the \(x\) direction, now using the usual notation.
Our original \(\beta = 0 \) curve cannot be endowed momentum in the \(x \) direction (my notation) because the \(x \) axis is contained in the \(2\omega \) plane at every \(t \). So let’s start by rotating the original curve through \(\frac{\pi }{2} \) in the negative direction round the \(z \) axis, to get the curve \(\psi _1 = \frac{i}{\sqrt{2} }\), \(\psi _4 = \frac{i}{\sqrt{2} } \) . We got the factor \(\frac{1}{\sqrt{2} } \) because of the way we defined the real amplitudes \(\psi _i \), and the factor \(i \) because of the way we defined the phases of the rotated curves. Let’s now look at the moment \(\omega t = \frac{3\pi }{2} \) of the rotated curve. In the original curve the momentary \(2\omega \) plane at \(\omega t = \frac{3\pi }{2} \) was \(x, - z \), and in the rotated curve it is \( - y, - z \). Rotating this in the negative direction round the \( - z \) axis generates momentum in the \( - x \) direction (my notation). So we have
And multiplying by \((-i)\):
Our \(( - x) \) is the usual notation’s \(y \), and it follows that this is our vector interpretation of the Dirac equation as a deterministic equation of motion in the case of a free particle in a spin \(z \) eigenstate \(\uparrow _z\) and with the momentum in the \(y \) direction (usual notation).
We must note that in order to get the \(x \) (my notation) momentum term we had to assume the superposed state \(\psi _1 = \frac{i}{\sqrt{2}},\psi _4 = \frac{i}{\sqrt{2} } \). I don’t think this is implicit in the Dirac formalism and I’m asking myself if any testable physical predictions are implied. I haven’t followed this up. Note that we could have achieved \(x \) (my notation) momentum by first rotating the curve through \(\frac{\pi }{2} \) round \(y \) and then looking at the \(\omega t = 0 \) moment of the rotated curve, but this, I think, would not fit into the Dirac equation. This too calls for further exploration.
We got momentum in the \(z \) direction by activating the wheels at \(\omega t = 0 \) and momentum in the \(y \) direction (my notation) by activating the wheels at \(\omega t = \frac{\pi }{2} \). Similarly we can get momentum in the \(\cos \alpha {\hat{z}} + \sin \alpha {\hat{y}} \) direction by activating the wheels at \(\omega t = \alpha \), assuming that the wheels generate a rotation round the momentary tangent to the \(2\omega \) flow. For example, at \(\omega t = \frac{\pi }{4} \) the momentary tangent to the \(2\omega \) flow point in the \( - x \) direction and the momentum we get by infinitesimally rotating the Frenet frame round the tangent in the negative direction is in the \(\frac{1}{\sqrt{2} }(z - y) \) direction. We can see this by imagining that the wheel-generated rotation is the only rotation taking place, and projecting the infinitesimal translation of our abstract point particle in the \(\frac{1}{\sqrt{2}}(z - y) \) direction relative to the center of the \(2\omega \) circle, generated by this rotation, on the \(y \) and \(z \) axes, noting that \(\frac{\partial |{\psi _4}|}{\partial y} \) and \(\frac{\partial |{\psi _3}|}{\partial z} \) are proportional to the magnitudes of the 2 projections respectively. Similarly, in the case of momentum in the \(x,y \) plane, the angle on the plane determines the phase coefficient of the \(\frac{\partial \psi _4 }{\partial y} \) term, and I think the generalization to momentum in a general direction follows naturally. I think that Hestenes [1] saw a part of this picture but interpreted it quite differently.
The Dirac equation, in the Dirac representation, is (usual notation):
We’ve discussed the first of the four equations. Ignoring signs for a moment, it is easy to see that we get the other three equations from similar considerations by starting with the rotated curves. Now, four terms have reversed signs that need explaining, namely, the \(\frac{\partial \psi }{\partial x} \) and \(\frac{\partial \psi }{\partial z} \) terms (my notation) of the second and fourth equations. I think the explanation is that the curves we start with in these two equations are the ones created by a rotation through \(\pi \) round \(x \) or \(z \) (my notation), which implies the reversal of the direction of the flow of physical time. Since we are using the same variable “time” as in the other two equations, the reversal of the direction of time implies a reflection \(y \rightarrow - y \). So instead of an equation that looks like \(\frac{\partial }{\partial y} = \cdots + \frac{\partial }{\partial y} + \frac{\partial }{\partial x} + \frac{\partial }{\partial z} \) we have an equation that looks like \(\frac{\partial }{\partial ( - y)} = \cdots + \frac{\partial }{\partial ( - y)} + \frac{\partial }{\partial x} + \frac{\partial }{\partial z} \), therefore we have to reverse the signs of the \(\frac{\partial \psi }{\partial x} \) and \(\frac{\partial \psi }{\partial z} \) terms.
I choose to stop at this point because I feel a more rigorous treatment of the basic issues is required before we can go on. My general idea as to the path on from here and to the full quantum picture has been outlined in the introduction, and I will not repeat it. Let’s just note again that due to the fast fluctuations in position in EMO space, an EMO combination can be observed as being in many places in physical space at the same physical time, and many EMO combinations can be observed at approximately the same physical place at the same physical time and be construed as components of the same physical particle. We may now however develop a slightly clearer notion of how fast these fluctuations need to be. It is reasonable to assume that fluctuations much faster than \(|{{\dot{\varvec{p}}}(t)}|\) in the position of a given EMO combination would make it impossible to continually identify the EMO combination as a component of a given physical particle, while an EMO combination whose position remains constant up to a velocity of \(|{{\dot{\varvec{p}}}(t)}|\) at a given \(\Delta t < \frac{\pi }{\omega } \) interval should in general be continually identified as a component of the same particle, maybe excepting some special cases. This may in a sense be our definition of a physical particle.
This last observation leads me to a guess concerning the quantum postulate regarding probability amplitudes. Think of an observer EMO combination and an observed physical particle. Say that during a continuous interval \((\Delta t)_1 < \frac{\pi }{\omega } \) the physical particle is in one physical state and during an interval \((\Delta t)_2 < \frac{\pi }{\omega } \) it is in a second state. (The discussion can readily be generalized to states defined by series of intervals \(\{{(\Delta t)_i}\}_1 \) and \(\{{(\Delta t)_j}\}_2\), and of course to more states). Let’s think of the picture as seen in the observer’s wandering EMO space, but assume that all the interactions happen at phases \(\omega t = 2\pi n \) of the observer so that we don’t have to consider the observer’s wandering EMO space’s oscillation relative to EMO space (I feel this needs to be said because we haven’t clarified the question of type (ii) interactions occurring at \(\omega t = \frac{\pi }{2},\frac{3\pi }{2}) \). In the wandering EMO space the rotation on the \(2\omega \) plane is explicit, not hidden in the complex phase, so that the observer actually moves with the speed of light along some curve. It occasionally has a glimpse of the observed particle’s state via a type (ii) interaction happening along a line defined by the momentary tangent to that curve. We may reasonably expect the observed particle to fluctuate with the speed of light in all directions, because the particle is made of many fluctuating EMO combinations, and the speed of light is the maximum fluctuation velocity allowed to any combination if it is not to forfeit its status as a component of the particle. (We remember that velocities in EMO space go to infinity, so there’s good reason to expect the speed of light to be reached at almost any \(t \) by at least some components).
Now let’s think of the bundle of segments defined by the observer and observed’s positions during the interactions, taking the curve the observer moves along as base space. The direction of each segment is momentarily parallel to the curve, but of course the curve curves in all directions. So it is not completely absurd to flatten this fiber bundle and approximate it as a plane spanned by a vector representing the direction of the curve and an orthogonal vector representing the direction of the segments. On this plane we have a square of side \((\Delta t)_1 c \) where the particle may be found in the first physical state (\( c \) being the speed of light), and a square of side \((\Delta t)_2 c \) where the particle may be found in the second physical state. Therefore, the probability of finding the particle in the \( j \)’ th state is best approximated by \(\frac{((\Delta t)_j c)^2}{\sum ((\Delta t)_i c)^2} \).
Our discussion so far revolved mostly around the free electron. I would like to end with a few preliminary and more speculative ideas concerning some other subjects. But before going on to that, let me add one last remark about a point which has intrigued me all along the work and in respect to which I have made no significant progress. We saw the concept of physical time emerge, together with other physical concepts, from the study of type (ii) interactions in EMO space. Meanwhile, we circumvented any questions concerning type (iii) interactions, as well as the immediate translations caused by type (ii) interactions (when we think of them as lasting for \(\Delta t > 0) \), and considered them only as a background noise. We didn’t even follow up on the question of the \(\omega t=\frac{\pi }{2},\frac{3\pi }{2} \) type (ii) interactions. Since so much of what is happening in EMO space seems to have only little regard to the flow of physical time, one cannot avoid wondering whether the study of these phenomena might hold some surprises in store, and especially, if superluminal signaling might in any way be implied.
6 More complex EMO combinations and hadron structure
Let’s try to speculate about the possible properties of more complex EMO combinations. We start with an observation concerning the combination we already know: An EMO’s ability to affect other EMOs depends on the angular velocity \(\varepsilon \omega \), and so is \(|{{\dot{\varvec{p}}}(t)}|\). There is therefore reason to expect a positive correlation between the strength of a particle’s action on other particles and the value of \(|{{\dot{\varvec{p}}}(t)}|\). This may all seem a bit nonsensical, since we have worked under the assumption of \(|{{\dot{\varvec{p}}}(t)}|\) being universally constant, and it was in fact implicit in our discussion that the universality of \(|{{\dot{\varvec{p}}}(t)}|\) is expressed in the physical results as the universality of the speed of light. However, the point may be valid if we discuss a combination in which even in the \(\beta = 0 \) case the effective focal point moves along a curve not restricted to a single plane in EMO space, so that \({\dot{\varvec{p}}}(t) \) has various projections on different planes, and the strength of the particle’s action on other particles is analyzed in terms of the contributions of the projections.
We also remember the speculation we brought up in connection with the mass term in the Dirac equation: If, in the case of a more complicated EMO combination, the \(\beta = 0 \) effective focal point moves along a complicated curve made of many little curls, where the effect of the wheels is to rotate some plane momentarily identified as the plane of the momentary curl, then the momentum endowed to the particle by the wheel-generated rotation may turn out to be proportional to the radius of a typical curl, so that mass turns out to be proportional to the curvature of the effective focal point’s curve.
Now let’s do a very naïve units check to connect these two observations: Think for example of the coulomb force, we have \(F = \frac{q^2}{r^2} = ma \), with the electrostatic unit of charge, grams, centimeters and seconds, implying that the units of \(\frac{q^2}{m} \) are \(\frac{\mathrm{length}^3}{\mathrm{time}^2} \), which works perfectly if mass is curvature and charge is velocity (and I’m now taking the risk of confusing \(t \) with time).
Let’s recall that the proton contains two \(u \) quarks and one \(d \) quark, with charges \(\frac{2}{3} \) and \( - \frac{1}{3} \). Obviously \(\sqrt{\left( {\frac{1}{3}} \right) ^2 + \left( {\frac{2}{3}} \right) ^2 + \left( {\frac{2}{3}} \right) ^2} = 1 \). Now imagine an EMO combination whose effective focal point moves in EMO space with a velocity that has a projection of constant magnitude \(\frac{1}{3}\left| {{\dot{\varvec{p}}}(t)} \right| \) on one of three orthogonal planes and projections of constant magnitude \(\frac{2}{3}\left| {{\dot{\varvec{p}}}(t)} \right| \) on the two others. Could this lead to a particle whose components have in some sense electrical charges of magnitudes \(\frac{1}{3} \) and \(\frac{2}{3} \)?
If it turns out that the proton can be explained in such terms, we would get a framework where the color degrees of freedom in QCD correspond to the freedom to choose one of three orthogonal planes in EMO space as representing a given EMO combination in an interaction with another combination, where the second combination also has the freedom to choose a representative out of three orthogonal planes. The fact that the three quarks in a baryon have different colors would correspond to the stipulation that all baryons be made of EMO combinations that have three orthogonal body planes. Quark confinement may be easily explained in such context if the properties of quarks, such as their electrical charges, arise from the interaction between the orthogonal body planes, while each body plane separately may not be identifiable as a quark at all. To make my point clearer I will now present an unexamined speculation as to the structure of the components of the proton, in which I will use three orthogonal body planes, each identical to the electron body plane.
We begin with three body planes of the type we already know, with \(\frac{\varepsilon d}{\sqrt{2} } = 1 \). Place one of the body planes on the \(x,y\) plane so that one body focal point is at \((0, - \frac{d}{\sqrt{2} },0) \) and the other at \((\frac{d}{\sqrt{2} },0,0)\), and the effective focal point is at \((0,0,0) \). Place a second body plane on the \(y,z\) plane so that one body focal point is at \((0,\frac{d}{\sqrt{2} },0) \) and the other at \((0,0,\frac{d}{\sqrt{2}})\), and the effective focal point is at \((0,0,0) \). Place the third body plane on the \(x,z\) plane so that one body focal point is at \((\frac{d}{\sqrt{2} },0,0) \) and the other at \((0,0,\frac{d}{\sqrt{2} }) \), and the effective focal point is at \((0,0,0) \).
The \(x,z\) body plane is intended to act as a link between the two other body planes. One of the \(x,z\) focal points will always move with an \(x,y\) focal point, and the other will always move with a \(y,z\) focal point. Each of the two other body planes has one free focal point, not constrained to move with a focal point belonging to any other plane. I suspect that if we were to move the free \(x,y\) focal point from \((0, - \frac{d}{\sqrt{2} },0) \) to \((0,\frac{d}{\sqrt{2} },0) \), thus constraining the two free focal point to move together, we would be imposing impossible restrictions which would cause the combination to break. My hope is that the suggested structure would allow just enough freedom to guarantee stability.
The relative phases of the three body planes are determined by our discussion of the projections of the effective focal point’s velocity, as we stipulate that the directions of the three projections be pairwise orthogonal at all \(t \). We can for instance fix the phases so that at \(\omega t = 0 \) the \(x,y\) effective focal point move in the \(y \) direction, the \(y,z \) one move in the \(z \) direction, and the \(x,z \) one in the \(x \) direction, and at \(\omega t = \frac{\pi }{2} \) the directions be \( - x,-y \) and \(z \) respectively.
What we need, beside stability, is for the dynamics to guarantee the constant magnitudes of the three projections. Assuming we have that, and denoting the magnitude of the \(x,z\) projection by a fraction \(0<\alpha <1\), we should then expect the magnitude of the two other projections to be \(\sqrt{\frac{1 - \alpha ^2}{2}} \), on symmetry grounds. If we prove \(\sqrt{\frac{1 - \alpha ^2}{2}} = 2\alpha \) we then have it that the fractions are \(\frac{1}{3} \) and \(\frac{2}{3}\) as required. Thinking of the a-symmetry between matter and anti-matter in physics, there’s satisfaction in thinking that, if all this works out and we also get the charge signs right, an EMO combination belonging to a proton and an EMO combination belonging to an electron, taken together, will turn out to contain four similar elements, two of which have positive charges and two negative.
Supposing we get all that, we can then start examining the motion of the entire proton EMO combination, whether this should involve adding wheels, or just manipulating the relations between the body planes. Hopefully, one would be able to distinguish two types of interactions: one similar to our type (ii) interactions, involving external EMOs whose focal points are distant, and the other having to do with the construction of more elaborate structures, where some external body plane attaches itself directly to one of the proton body planes by superposing its focal points on some of the proton focal points. Understanding this last type may, I hope, lead to an EMO theory description of the strong interaction.
7 Gravity
We’ve seen that far away from the body focal points the body plane resembles an EMO with the effective focal point as focal point. To keep things simple let’s approximate the motion of the effective focal point as a rotation on a circle of radius \(1 \) with the origin as center, on the \(x,y \) plane. Let’s assume that no other EMOs share that plane and that no other focal points lie on it. Let’s also assume that the intersections of other EMO planes with the body plane are equally distributed so that they mark an even grid on the body plane, and that the grid is dense so that the distance between grid lines is much smaller than 1.
Now let’s add an external EMO whose plane differs from the body plane and whose focal point is on the body plane and serves as a test particle. We assume that this test particle is far from the body focal points, so that that we can think of the body plane as the plane of a unified EMO and therefore, the unified EMO azimuthal velocity at the test particle is well defined. Our discussion will involve the idea of the test particle being first carried about by some external EMO and than being taken by our unified EMO, only to be snatched away again by some external EMO. Recall that we assumed an EMO (1) would snatch a test particle away from another EMO (2) if the velocity that EMO (1) affected on the test particle were greater than the velocity EMO (2) affected on the test particle, where these two velocities are: 1) The \(R^3 \) vector sum of the velocity of focal point (1) and the azimuthal velocity of EMO (1) at the test particle’s position. 2) The \(R^3 \) vector sum of the velocity of focal point (2) and the azimuthal velocity of EMO (2) at the test particle’s position. In the following discussion we will be interested in the probability of the unified body EMO snatching the test particle away from an external EMO, and therefore our discussion will involve velocities averaged over long periods of time. Since we assume that the test particle is far from the effective focal point of the unified EMO, we will be able to neglect the effective focal point’s velocity and consider just the average azimuthal velocity of the unified EMO at the test particle’s position. As for the external EMO, we will just refer to its velocity at the test particle’s position, neglecting to differentiate the azimuthal velocity contribution from the focal point velocity contribution.
Let’s consider two kinds of events:
-
(a)
The test particle, which has previously been carried by an external EMO, gets caught by the body unified EMO when its path intersects its plane, and this happens at the point \((0,D,0) \), where \(D \gg 1 \), and at a moment when the effective body focal point is at \((0,1,0)\). Let’s also assume for now that the test particle is carried by the body unified EMO for exactly a quarter of a cycle and is snatched away by some external EMO when the effective focal point is at \((1,0,0) \). It follows that the test particle, beside being translated by the oscillation of the body unified EMO half line that carries it, is also translated a distance of \( - 1 \) along the \(y \) axis due to the motion of the effective focal point. (The translation along \(x \) is of no interest to us, as will shortly become evident).
-
(b)
The test particle gets caught by the body unified EMO at \((0,D,0) \) when the effective focal point is at \((0, - 1,0) \) and is carried for a quarter of a cycle. In this case the relevant contribution of the effective focal point’s motion to the test particle translation is a \( + 1 \) translation along the \(y \) axis.
Averaging on many events so that the translations caused by the azimuthal velocities can be ignored, we get that the type (a) events tend to attract the test particle toward the origin, which is the effective focal point’s average position, and the type (b) events tend to repulse it.
The magnitude of the body unified EMO azimuthal velocities involved in type (b) events would tend on average to be a little greater than those involved in type (a) events, because the effective focal point would be closer to \((0,D,0) \) in type (a) events. This leads to two observations:
-
1.
Type (b) events are a little more frequent than type (a) events, since the bigger average body unified EMO azimuthal velocity at \((0,D,0) \) when the effective focal point is at \((0, - 1,0) \) makes for a greater probability of the body unified EMO snatching the test particle from an intersecting EMO plane, compared with the probability of this happening when the effective focal point is at \((0,1,0) \). For the same reason, type (b) events will have a slightly better chance of keeping the test particle on the body plane when crossing intersection lines.
-
2.
If we only compare pairs of type (a) and type (b) events with test particle paths of equal length, the type (a) events will on average have a longer duration than the type (b) events, because the type (a) velocities would on average be smaller.
Now we add the assumption of small \(D \gg 1 \), where by small we mean that there exist \(D' \gg D \) such that a ball of radius \(D' \) round the origin contains only a negligible fraction of the total number of focal points in EMO space. Let \( v(a) \) and \(v(b) \) be the average azimuthal velocities of the unified body EMO at \((0,D,0) \) in the type (a) and type (b) cases, respectively. Let \(u \) be the average velocity at \((0,D,0) \) of all the external EMOs intersecting the body plane there. Under the assumption of a small \(D \gg 1 \) we have:
Let’s ask which observation, (1) or (2) is more significant. We can think of \(\frac{v(b) - v(a)}{u} \) as a measure of the significance of observation (1), and of \(\frac{v(b) - v(a)}{v(a)} \) as a measure of the significance of observation (2).
Under the assumption of small \(D \gg 1 \) we have \(\frac{v(b) - v(a)}{u} \ll \frac{v(b) - v(a)}{v(a)} \), and we therefore conclude that observation (2) is much more significant than observation (1): We can think of type (a) events as being practically as frequent as type (b) events and lasting on average for practically as many grid lines as type (b) events, and therefore lasting longer, on average, than the type (b) events.
Assuming that the grid of intersections with external EMO planes is dense (the distance between grid lines being much smaller than 1), we expect most events to last much less than a quarter of a cycle. The above conclusion concerning the (a) and (b) events can be generalized to events where the test particle gets caught at \((0,D,0) \) at a general phase of the effective focal point’s rotation: the greater the \(y \) value of the effective focal point’s position during the event, the longer, on average, will be the duration before the test particle is snatched away by some external EMO. Thinking of the accumulated effect of many such events, with the test particle being caught and released many times, we conclude that the test particle will tend to be drawn toward the negative \(y\) direction.
It follows that under the assumption of small \(D \gg 1 \) there exists an attractive force between EMO combinations. Since this effect depends on the very slight difference in duration between type (a) and type (b) events, we can reasonably expect it to be small in comparison with the dynamical implications of type (ii) interactions. This also works well with the idea of mass as curvature: If the radius of the rotation of the effective focal point where smaller than 1, the attractive force would be greater, because the path of a test particle carried by the body plane for a very short duration would be less like a straight segment in the tangent direction. Thinking now of the EMO space path of a hypothetic effective focal point as made of many little curls lying on different planes, the smaller the radius of a curl, the greater is the attractive force in its plane. These ideas seem to me to hold the best promise of deducing a theory of gravity from EMO theory.
What leaps to the eye is that gravity deduced this way might turn out to be a medium range phenomenon: On the one hand, since we had to stipulate \(D \gg 1 \), it seems that the attractive force would disappear for very small \(D \) (certainly for \(D < 1) \), and on the other hand, if we assume a finite number of EMOs in EMO space, we encounter a completely new situation whenever the condition of small \(D \gg 1 \) is not met, and though I have not analyzed this situation, there’s reason to expect that on the largest scale, the attractive force will at least weaken, if not disappear or become repulsive. Another thing that one could maybe expect is that such a theory of gravity would strongly depend on the geometry of the specific problem: for instance, the two dimensionality of EMOs and body planes may lead to a stronger attractive force in the case of disk-like objects, compared with the case of spherical symmetry. Things become of course much more complicated when we recall that we are now only discussing attraction and repulsion in EMO space, while we are yet to figure out the implications for physical space.
It is anybody’s guess if such a theory of gravity, should it really be developed, might account for the considerable discrepancy that seems to exist between our understanding of spacetime, as it emerges from EMO theory, and the point of view of big-bang cosmology. I would now like to make a basic observation about EMO space that might perhaps have some bearing on this problem.
We have described the momentary state of EMO space as representing the hypersphere, but, except for the reference we made to this while discussing the transformation rule of moving EMOs, we really only used the correspondence with \(S^3 \) once, in the wandering EMO procedure. Lacking a deeper understanding of EMO space, this may leave us with two very different possible interpretations of the connection between EMO space and \(S^3 \), which can be called the soft interpretation and the hard one. The soft interpretation corresponds to a mental picture where there is a separate hypersphere tangent to EMO space at each focal point. This approach may enable the wandering EMO procedure without enforcing a dependence of the distribution of focal points in EMO space on a distribution of points in the hypersphere. If we adopt the soft interpretation, our only hope of reconciling our ideas with cosmological observation probably lies in the above idea of repulsive large scale gravity. However, the hard interpretation, which seems in some ways more consistent with the overall spirit of this paper, opens a completely different perspective. The hard approach is where we say that EMO space in its entirety represents the hypersphere, so that one can move between the points of view of different focal points in EMO space and maintain a one to one correspondence between the momentary coordinates of all focal points and specific points in the hypersphere.
To start exploring the possible implications of the hard approach, suppose for a moment that the momentary positions of EMO focal points in EMO space correspond to an equal distribution of points in \(S^3 \). Then, choosing any one focal point to be the origin of the axes in EMO space, we get that the density of focal points in EMO space decreases with the distance from the origin, as dictated by the stereographic projection. Choosing another focal point as observer then implies an \(R^3 \) diffeomorphism which rearranges the focal points, so that once again the density is maximal near the observer. Let’s now ask what would follow if we introduced the idea that some physical phenomena may depend on the average density of focal points decreasing with the distance between the observed phenomenon and the observer. Suppose for example that the EMO space discussion of the energy levels of electrons in atoms would in fact involve structures whose typical size depends on the local density of focal points. Since any observer’s point of view would be that the average density of focal points tends to decrease with the distance, we may end up with a picture in which, as the observed atom becomes more distant from the observer, the internal distances grow larger, leading to the emitted photon wavelengths growing longer with distance, so that redshift is observed.
This line of reasoning might in the end beget something a little similar to a tired light cosmology, with the difference that instead of losing their energy along the way toward the observer, distant photons are emitted less energetic to begin with. So according to this, tired light would be understood as a property of spacetime, and the very same property of spacetime would also account for the time dilation of observed astrophysical phenomena. This would not necessarily imply a completely static universe, as one would also have to take into account the cosmological scale predictions of whatever theory of gravity we end up with.
All this is of course mere speculation, but we must note that the consequences of adopting the hard approach may not end there. According to this interpretation, any momentary structure that we observe from a given focal point’s point of view will be deformed when we look at it from the point of view of some other, distant, focal point. Such an approach might make EMO combinations less real, in a sense, and interpret them as patterns that we look for while observing EMO space from the point of view of a given focal point, rather than objective entities that exist regardless of point of view. It seems to me that physically, this might amount to the rather shocking proposition that the information we get when watching distant parts of the universe may be scrambled, and not resemble the picture that we would see if we actually traveled there.
Adopting the hard approach, in spite of the difficulties, may turn out to be a first step towards understanding the origin of EMOs. Remember that in the discussion of our 4-EMO combination, we assumed \(\varepsilon \rightarrow 0,d \rightarrow \infty \), which implies that from the effective focal point’s point of view the points represented by focal points (1) and (2) are close together in \(S^3 \). If we imagine, for argument’s sake, that we start with an equal distribution of focal points in the hypersphere at some \(t \), then thinking of \(\varepsilon \rightarrow 0\), \(d \rightarrow \infty \) leads to the idea of taking the density of points in \(S^3 \) to infinity, or equivalently, taking the density of points in \(R^4 \) to infinity. But as we add more EMOs to EMO space, these EMOs interact, and, in some sense, it becomes increasingly difficult to maintain EMO space self consistency. This might suggest the idea of physical reality emerging from the conflict between, on the one hand, the wish to approximate the continuity of the real numbers in \(R^4 \) by increasing the density of focal points in EMO space, and on the other hand, the demands of EMO space self consistency.
It was the idea of approximating the continuity of \(R^4 \) by increasing the density of focal points, which lead me to make a previous comment about the number of EMOs in EMO space being large. On the other hand, I would like to consider the idea that the density of points in \(S^3 \) which can be represented as EMO focal points may turn out to be bounded by the demands of EMO space self consistency. This speculation doesn’t seem reasonable because as long as we only consider single EMOs, no scale is involved. But, since we expect physical scale to be determined by our \(\frac{\varepsilon d}{\sqrt{2} } = 1 \) requirement, I suspect that there may be a chance of the \(S^3 \) point density turning out to be bounded by the requirements of EMO combination stability. And, assuming that the requirement \(\frac{\varepsilon d}{\sqrt{2} } = 1 \) determines the electron’s Compton wavelength, one can hope to find the Planck length eventually emerging from the implications of the limit on \(S^3 \) point density to the density of the grid of intersections with external EMO planes.
But why would EMOs exist at all? Why would adding a point in \(S^3 \) to be represented as an EMO focal point entail the generation of oscillations on some sphere in \(S^3 \), to be represented by the oscillations on the EMO plane? I’ll suggest a simple explanation which is possibly the most radical idea presented in this paper, and is unfortunately only a germ of an idea, still needing a great deal of thinking through. The discussion will involve oscillations on a circle, and can, perhaps, be applied equivalently either to the oscillations on an EMO plane in \(R^3 \) or directly to the oscillations on the sphere in \(S^3 \) represented by the EMO plane.
Recall the construction of the real numbers. It is motivated, as I understand, by the geometrical notion of the straight line and the observation that the rational numbers can only represent discrete points on such a line. This leads to the various equivalent constructions of the real numbers, which fill the gaps and allow us to identify any point on the line with a real number. Two of the best known constructions, which, like many students, I encountered in a first course in calculus, define the real numbers as equivalence classes of Cauchy series of rationals or as Dedekind cuts in the set of rationals. If, after defining \(R \), we think of the Euclidean plane in terms of the cartesian product \(R\times R \), we seem to have no problem in accepting the idea of continuous plane curves, for instance, the unit circle in \(R^2 \).
I would now like to adopt a different point of view: let’s pursue a similar line of thought, but start from the geometrical notion of a circle of radius 1, instead of the notion of a straight line. So, using the rational numbers, our current mission is to construct a system of numbers that will allow us to identify each point on the circle with a number, that is, an angle. But the geometrical notion of a circle comes with the premise of identifying the angles 0 and \(2\pi \). This simple fact renders our current endeavor incompatible with the definition of the real numbers, since 0 is rational and \(2\pi \) is irrational. Obviously, we can’t define the real angles so that the angle \(0 = 2\pi \) be defined as both rational and irrational.
Of course, any neighborhood of 0 contains irrational numbers, so we can start with the usual construction of the real numbers on the real line, and then identify \(2\pi \) with an irrational number \(x \), as close as we wish to 0. But this line of thinking is symmetrical in regard to the sign of \(x \): we may equally think of the angle \(2\pi \) as being infinitesimally dislocated from 0 in the positive or the negative direction. Another problem is that if we make a change of coordinates by rotating the circle through some real angle \(\theta \), we also move the dislocation from 0 to \(\theta \). These two problems, together with the wish to define a unit circle with perimeter \(2\pi \), lead to the definition of the EMO, where we should think of the unit circle on the EMO plane along the entire cycle as our fundamental geometrical object: a circle of radius 1 and perimeter \(2\pi \) where each point oscillates round the respective fixed point in the background plane. From this point of view we must perhaps interpret the continuous EMO oscillation as an approximation of a non-continuous oscillation on the irrationals, skipping rational numbers. Thinking of EMOs this way, it makes sense that we got all our results by taking \(\varepsilon \rightarrow 0 \): it is by taking the amplitude of the oscillations to zero that we make the dislocation of \(2\pi \) from 0 tend to zero.
What I seem to be proposing is that the geometrical concept of angle can only be formulated as a limit, where some oscillation’s amplitude tends to zero. EMO theory then deals with the structures created by these infinitesimal oscillations, while placing them against the idealized background of \(\varepsilon = 0 \). I have not considered possible generalizations to other numbers of dimensions, but EMO space as we have seen it—corresponding to \(R^4 \)—may perhaps arise from the opportune possibility of, in some sense, identifying the flow generated by these infinitesimal oscillations with the Hopf flow. It’s early days, and as my understanding of EMO theory is still very limited in every respect, I stop here.
Reference
Hestenes, D.: The zitterbewegung interpretation of quantum mechanics. Found. Phys. 20, 10 (1990)
Acknowledgments
Yuval Eitan contributed helpful discussions in the early stages of the work. Rafi and Miriam Eitan sponsored the work. I also wish to thank Gadi Moran, Eliahu Cohen, Shahn Majid, Boaz Klartag, Yakir Aharonov, Uri Kol and Nima Gefen for discussions, support and encouragement.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Eitan, S. Toward a geometrical foundation for physics. Quantum Stud.: Math. Found. 2, 89–129 (2015). https://doi.org/10.1007/s40509-014-0022-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40509-014-0022-6