Abstract
We demonstrate that policies aimed at reducing frictional unemployment may lead to the opposite results. In a labor market with long-term wage contracts and moral hazard, any such policy reduces employees’ opportunity costs of staying on a job. As employees are less worried about losing their job, a smaller share of employees is willing to exert effort, leading to a lower average productivity. Consequently, firms create fewer vacancies, resulting in lower employment and decreased welfare.

Similar content being viewed by others
Notes
Prominent examples are tax deductibility for job search expenses in the US (IRS Publication 529, 2011, p. 5; see also Garrison and Cummings 2010), and unemployment benefit programs with provisions that an individual maintains the status of “job seeker” such as Jobseeker’s Allowance (UK), Newstart Allowance (Australia), Employment Insurance (Canada), and the Unemployment Benefit (New Zealand), to name a few.
This is without taking into account the cost of running such schemes which is an additional toll on the social welfare.
Under certain assumptions, an increase in unemployment benefits can mitigate, rather than aggravate, the incentive problem, by promoting flow into (and creation of) high-productivity jobs (Acemoglu and Shimer 2000) or through increasing the equilibrium performance-based component of the wage contracts (Demougin and Helm 2011).
This role remains qualitatively unchanged when incorporating matching friction and involuntary unemployment, as we discuss in Sect. 2 below.
Other related papers are Guerrieri (2008) and Matouschek et al. (2009). Guerrieri (2008) is concerned about inefficiencies in a dynamic search model where workers’ disutility from labor is subjected to random shocks; Matouschek et al. (2009) study the effect of the separation cost on the willingness of firms and employees to invest into continuation of the relationship after an exogenous shock.
Here, unemployed has its literal meaning of not being employed. This term does not make a distinction between jobless individuals who are looking for a job and who are not.
The search cost is exogenous and it does not include any foregone wages while being unemployed.
This assumption is made for clarity of exposition; it is not crucial for the results (as discussed at the end of this section).
We do not restrict strategies of the market participants to stationary ones—we consider equilibria where deviations to nonstationary strategies are not beneficial.
Assuming that there is a sufficient mass of individuals with high cost of effort who prefer to shirk even if the differential between the initial and subsequent wages is large.
The tie is a zero probability event and thus can be ignored.
We ignore a measure zero of individuals who are indifferent.
For \(s = \beta (\pi -u_0)\) both statements are true.
This can be replaced with \(\lambda ^*\) of individuals with types \(c\ge \alpha \delta s\) participating and the rest staying out, or any of a continuum of payoff-equivalent equilibria that maintain a mass \(\lambda ^*\) of this group participating in expectation. So long as the expected mass \(\lambda ^*\) is preserved, which individuals participate and which stay out is arbitrary (recall that the type of these individuals is irrelevant, since they shirk whenever employed).
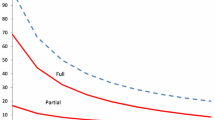
The plot is done for the values of parameters \(\alpha =\delta =0.9\), \(\beta =1/2\), \(\pi =10\), \(u_0=s_F=1\) and F uniform on \([0,\alpha \delta \beta (\pi -u_0)]\).
That is not to say that the process we outline in this paper is the only one contributing to these regularities.
The assumption that firms create vacancies whenever indifferent is standard and can be justified, for example, that creating a vacancy is welfare improving. Note that this assumption has a bite only in the event of very low expected benefit from hiring an employee, \(J=s_F\). The results presented below are unaffected so long as this low threshold is not reached.
See the discussion at the bottom of Sect. 2.
Individuals with type \(c>w\) will not exert high effort. However, these individuals experience negative utility from labor, thus staying out of the labor market in equilibrium.
We assume this simple form of wage determination to keep the analysis straightforward and transparent. The interpretation is that w is a result of negotiations between firms and the employees union; from the perspective of an individual, w is exogenous. The results are not qualitatively affected if we model bargaining as a compromise of the two parties whose disagreement options are endogenously determined in the model.
The tie is a zero probability event and thus can be ignored.
For \(s = \beta (\pi -u_0)\) both statements are true.
This can be replaced with \(\lambda ^*\) of individuals with types \(c\ge \alpha \delta s\) participating and the rest staying out, or any of a continuum of payoff-equivalent equilibria that maintain a mass \(\lambda ^*\) of this group participating in expectation. So long as the expected mass \(\lambda ^*\) is preserved, which individuals participate and which stay out is arbitrary (recall that the type of these individuals is irrelevant, since they shirk whenever employed).
References
Acemoglu, D., Shimer, R.: Productivity gains from unemployment insurance. Eur. Econ. Rev. 44(7), 1195–1224 (2000)
Baily, M.N.: Some aspects of optimal unemployment insurance. J. Public Econ. 10(3), 379–402 (1978)
Blanchard, O.: The economic future of Europe. J. Econ. Perspect. 18(4), 3–26 (2004)
Chetty, R.: Moral hazard versus liquidity and optimal unemployment insurance. J. Polit. Econ. 116(2), 173–234 (2008)
Demougin, D., Helm, C.: Job matching when employment contracts suffer from moral hazard. Eur. Econ. Rev. 55(7), 964–979 (2011)
Diamond, P.A.: Mobility costs, frictional unemployment, and efficiency. J. Polit. Econ. 89, 798–812 (1981)
Diamond, P.A.: Wage determination and efficiency in search equilibrium. Rev. Econ. Stud. 49, 217–227 (1982)
Farber, H.S.: Job loss and the decline in job security in the united states. In: Abraham, K., Spletzer, J.R., Harper, M. (eds.) Labor in the New Economy, pp. 223–262. University of Chicago Press, Chicago (2010)
Fredriksson, P., Holmlund, B.: Improving incentives in unemployment insurance: a review of recent research. J. Econ. Surv. 20(3), 357–386 (2006)
Garrison, L.R., Cummings, R.: Global impact of tax considerations for displaced workers. Int. Bus. Econ. Res. J. (IBER) 9(9), 87–98 (2010)
Gregg, P., Wadsworth, J.: Job tenure in Britain, 1975–2000. Is a job for life or just for Christmas? Oxf. B Econ. Stat. 64, 111–134 (2002)
Grubb, D.: Eligibility criteria for unemployment benefits. In: Labour Market Policies and the Public Employment Service, OECD, pp. 187–216 (2001)
Guerrieri, V.: Inefficient unemployment dynamics under asymmetric information. J. Polit. Econ. 116(4), 667–708 (2008)
Holmlund, B.: Unemploymeny insurance in theory and practice. Scand. J. Econ. 100(1), 113–141 (1998)
Hopenhayn, H.A., Nicolini, J.P.: Optimal unemployment insurance. J. Polit. Econ. 105(2), 412–438 (1997)
Macaulay, C.: Job mobility and job tenure in the UK. Labour Market Trends 111(11), 541–550 (2003)
Manning, A.: You can’t always get what you want: the impact of the UK Jobseeker’s Allowance. Labour Econ. 16, 239–250 (2009)
Marimon, R., Zilibotti, F.: Unemployment vs. mismatch of talents: reconsidering unemployment benefits. Econ. J. 109(455), 266–291 (1999)
Matouschek, N., Ramezzana, P., Robert-Nicoud, F.: Labor market reforms, job instability, and the flexibility of the employment relationship. Eur. Econ. Rev. 53(1), 19–36 (2009)
Moen, E.R., Rosén, A.: Incentives in competitive search equilibrium. Rev. Econ. Stud. 78, 733–761 (2011)
Mortensen, D.T.: The matching process as a noncooperative/bargaining game. In: McCall, J.J. (ed.) The Economics of Information and Uncertainty. University of Chicago Press, Chicago (1982)
Petrongolo, B.: The long-term effects of job search requirements: evidence from the UK JSA reform. J. Public Econ. 93(11), 1234–1253 (2009)
Pissarides, C.A.: Equilibrium Unemploymeny Theory. The MIT Press, Cambridge (2000)
Pries, M., Rogerson, R.: Search frictions and labor market participation. Eur. Econ. Rev. 53(5), 568–587 (2009)
Rayner, E., Shah, S., White, R., Dawes, L., Tinsley, K.: Evaluating Jobseeker’s Allowance: a summary of the research findings. Department of Social Security (UK), Research Report 116 (2000)
Shapiro, C., Stiglitz, J.E.: Equilibrium unemployment as a worker discipline device. Am. Econ. Rev. 74(3), 433–444 (1984)
Shavell, S., Weiss, L.: The optimal payment of unemployment insurance benefits over time. J. Polit. Econ. 87, 1347–1362 (1979)
Tsuyuhara, K.: Dynamic contracts with worker mobility via directed on-the-job search. Int. Econ. Rev. 57(4), 1405–1424 (2016)
Acknowledgements
This paper was conceived during the activities of the Game Theory and Evolution group organized by Sergiu Hart and Avi Shmida and hosted by the Institute for Advanced Studies and the Center for Rationality at the Hebrew University of Jerusalem. We are thankful to the group members, in particular to its organizers and the host institutions. We also thank Tomer Blumkin, Leif Danziger, Tymofiy Mylovanov, and Eyal Winter for valuable comments.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: Proofs
Appendix: Proofs
1.1 Proof of Proposition 1
Proposition 1
In the model with no moral hazard, a reduction of the job search cost is welfare improving.
The proof is divided into four subsections.
1.1.1 Labor demand
Denote by x and y the masses of searching individuals and firms, respectively, and by X and Y the masses of active individuals (that are searching or producing) and active firms (that have a filled job or a vacancy), respectively. Let J and V be a firm’s value of a filled job and a vacancy, respectively. Let \(\mu _F\) be the probability to fill a vacancy in a given period, \(\mu _F= \min \{x/y,1\}\). Then
Assume that firms create vacancies so long as \(V>0\) and withdraw them if \(V< 0\). If \(J< s_F\), then \(V<0\) for all \(\mu _F\), and hence, there will be no labor demand, \(Y=0\). However, if \(J\ge s_F\), then in steady state, \(V=0\) must hold, and hence, \(\mu _F\) must satisfy
Since \(s_F/J=\mu _F\equiv \min \{x/y,1\}\), then either \(s_F/J<1\), and hence \(x/y< 1\), or \(s_F/J=1\), and hence \(x/y\ge 1\). Moreover, in the latter case, it must be \(x/y= 1\), because we have assumed that firms create vacancies so long as the cost of maintaining one, \(s_F\), does not exceed the expected benefit, J.Footnote 18 Therefore, if \(y<x\), then new vacancies will be created until \(y=x\). Consequently, the mass of job searching individuals does not exceed the mass of vacancies, so every individual finds a job immediately with certainty.Footnote 19
Let us now derive the mass of active firms, Y. Denote by \(\gamma \) the fraction of individuals that are employed at the beginning of each period. Then
Combining (A.1) and (A.2) yields:
1.1.2 Labor supply
In the benchmark model, there is no moral hazard, so all employees exert high effort.Footnote 20 Hence, firms will never dismiss workers. The fraction of individuals who lose their jobs and return to the job market is given by job destruction rate \(1-\alpha \). The total revenue created by a filled job position net of the unemployment income (for short, surplus) is, therefore, equal to:
Similarly, a firm’s gross value of filling a vacancy is equal to:
We assumed that a firm’s share of the surplus is \(1-\beta \), so \(J=(1-\beta )S\), and hence, the wage is given byFootnote 21:
Let us now determine the equilibrium behavior of an individual with cost of effort c.
Lemma 5
An individual of type \(c\in {\mathbb {R}}_{+}\) participates in the job market if and only if
Proof
Since we are considering equilibria in steady state only, it is sufficient to compare the lifetime utility of the individual who is always active and the one who is always inactive. The utility of an inactive individual of type c is given by (3) in the main text, restated here:
Now, consider an active individual of type c. Denote by \(U_{\mathrm{H}}(c)\) her lifetime utility starting from a period where she is unemployed (subscript H stands for “high effort” for consistency with notations in further sections). Note that in the period where she is employed, her lifetime utility is simply \(U_{\mathrm{H}}(c)+s\), as in a steady state, the only difference between being employed and unemployed is the job search cost (as we have established above that individuals find a job immediately with probability one). This yields (1) in the main text, restated here:
Consequently, an individual of type c will participate in the labor market if and only ifFootnote 22\(U_{\mathrm{H}}(c)>U_0\), or
which, together with (A.4), yields the result. \(\square \)
Intuitively, an individual will participate in the labor market if her cost of effort is small relative to the expected wage, net of the unemployment income, and expected costs of job search. Denote by \({\bar{c}}(s)\) the critical type who is indifferent between participating or not:
1.1.3 Steady state
We are now in position to find the masses of active individuals and active firms, X and Y, in steady state.
First, by Lemma 5, only individuals of type \(c<{\bar{c}}(s)\) will be active, and hence
Next, a firm’s value of a filled job is given by:
Finally, after every period fraction, \(\alpha \) of active individuals remain employed, and thus, \(\gamma =\alpha \). Consequently, by (A.3):
Note that if the individuals’ search cost is high enough, \(s\ge \beta (\pi -u_0)/(1-\alpha \delta )\), then no individuals participate and the labor market collapses (since in that case \({\bar{c}}(s)\le 0\) and \(F({\bar{c}}(s))=0\), so we have \(X=0\)). Similarly, if the firms’ advertising cost is high enough, \(s_F> J=(1-\beta )(\pi -u_0)/(1-\alpha \delta )\), no firms are willing to open vacancies, so we have \(Y=0\) and the labor market collapses. For the rest of the paper, we assume that \(s_F\le (1-\beta )(\pi -u_0)/(1-\alpha \delta )\).
1.1.4 Comparative statics
Let us analyze the relationship between an individual’s job search cost and the welfare. As in this model, search cost s represents a pure waste, it is very intuitive that a reduction of s leads to welfare improvement.
Indeed, consider a reduction of the search cost from s to \(s'\). Then, the mass of the individuals who search for jobs weakly increases, as \(s>s'\) entails \({\bar{c}}(s)<{\bar{c}}(s')\), and consequently, \(F({\bar{c}}(s))\le F({\bar{c}}(s'))\). Any individual who is participating under \(s'\) is strictly better off relative to s, as her utility has gone up due to the lower search cost. Any individual who is inactive under \(s'\) is indifferent between s and \(s'\), as her utility remains unchanged, \(u_0/(1-\delta )\). Hence, the consumer surplus strictly increases as s goes down.
Next, firms with filled job positions make profit \((1-\beta )(\pi -u_0)\) in a single period. Under \(s'\), the mass of firms engaged in production is larger, and so is the total producers’ surplus. \(\square \)
1.2 Proof of Theorem 1
Theorem 1
-
(A)
There exists an equilibrium with positive participation if and only if \({\underline{s}}\le s<{\bar{s}}\).
-
(B)
The equilibrium with positive participation is unique. If \(s\ge \beta (\pi -u_0)\), then it coincides with that in the benchmark model. If \(s\le \beta (\pi -u_0)\),Footnote 23 then it is characterized by:
-
(i)
the equilibrium wage is \(w=u_0+s\);
-
(ii)
every individual of type \(c<\alpha \delta s\) participates with probability one and exerts high effort; every individual of type \(c\ge \alpha \delta s\) participates with probability \(\lambda ^*\) and exerts low effort,Footnote 24 where
$$\begin{aligned} \lambda ^*=\frac{(1-\alpha )F(\alpha \delta s)}{(1-\alpha \delta )(1-F(\alpha \delta s))}\cdot \frac{\beta (\pi -u_0)-s}{\beta u_0+s}. \end{aligned}$$(4)
-
(i)
1.2.1 Part (B)
We will prove that if there exists an equilibrium with positive participation, then it is unique and satisfies the conditions stated in Part B.
Recall that we focus on stationary equilibria. In particular, the best reply of a firm to a stationary strategy of the individuals (Lemma 1) and the best reply of individuals to a stationary strategy of firms (Theorem 1) are stationary. In other words, no market participants can benefit by deviating to nonstationary strategies.
Denote by p the probability that a newly hired worker has type \(c<c^*(s)\) and thus will exert high effort when employed. Then, surplus S produced by a filled job vacancy is given by:
where \((\pi -u_0)/(1-\alpha \delta )\) is the surplus from an employee who always exerts high effort (as S in Sect. 3) and \((-u_0)\) is the surplus from an employee who shirks in the first period and loses the job at the end of that period.
Similarly, the value J of a filled job vacancy for a firm is given by:
where w is the equilibrium wage. Recall that wage determination rule requires:
As J is strictly decreasing in w and \(J=S\) for \(w=u_0\), for any given p, there exists a unique w that solves (A.8).
Suppose that \(s>\beta (\pi -u_0)\). By the wage determination rule, the wage cannot exceed its feasible maximum \(u_0+\beta (\pi -u_0)\), and hence, \(w<u_0+s\). This corresponds to case (a) in Corollary 1, where all individuals who participate exert high effort, \(p=1\). Then, we have \(S=(\pi -u_0)/(1-\alpha \delta )\) and \(J=(\pi -w)/(1-\alpha \delta )\). Solving (A.8) for w yields \(w=u_0+\beta (\pi -u_0)\). Note that this is the same equilibrium as in the benchmark model.
Next, suppose that \(s<\beta (\pi -u_0)\). Corollary 1 implies the following labor market composition. The total mass of active individuals with type \(c<c^*(s)\) is \(F(c^*(s))\), of which only fraction \(1-\alpha \) lose their jobs and return to the labor market. Hence, the mass of individuals with type \(c<c^*(s)\) on the labor market constitutes \((1-\alpha )F(c^*(s))\). Next, the total mass of individuals with type \(c\ge c^*(s)\) is \(1-F(c^*(s))\), of which some fraction \(\lambda \in [0,1]\) are active. Hence, the mass of individuals with type \(c\ge c^*(s)\) on the labor market constitutes \(\lambda (1-F(c^*(s)))\). Consequently, the probability that a newly hired worker has type \(c<c^*(s)\) and thus will exert high effort is given by:
Consider case (c) in Corollary 1 that stipulates \(w=u_0+s\), so condition (i) holds. Then, there is a unique value of \(\lambda \) that solves (A.8) and it is equal to \(\lambda ^*\) that can be easily verified. Thus, we have proved that the equilibrium must satisfy condition (ii). Yet, we need to verify that \(\lambda ^*\in [0,1]\). We have assumed that \(s\le \beta (\pi -u_0)\), and thus, \(\lambda ^*\ge 0\). Also, we have assumed that F first order stochastically dominates the uniform distribution on \([0,\alpha \delta \beta (\pi -u_0)]\), that is:
for all \(s\in [0,\beta (\pi -u_0]\). Hence, we have \(F(c^*(s))\beta (\pi -u_0)\le s\) for all \(s\in [0,\beta (\pi -u_0)]\). Consequently
Next, let us show that cases (a) and (b) in Corollary 1 cannot occur in equilibrium. It was shown above that case (a) entails \(s>\beta (\pi -u_0)\), a contradiction. It remains to consider case (b) that stipulates \(w>u_0+s\) and \(\lambda =1\). Then, we have:
Equation (A.8) can be rewritten as:
Solving for \((w-u_0)\), we obtain:
where the third line is by (A.10) and the last line is due to:
However, we have assumed \(w>u_0+s\), a contradiction.
1.2.2 Part (A)
First, we show that \(X=0\) for \(s\ge {\bar{s}}\). For \(s>\beta (\pi -u_0)\), the equilibrium (if it exists) is the same as in the benchmark model, and by Lemma 5, an individual of type c participates in the labor market if and only if \(c<{\bar{c}}(s)\). However, for \(s\ge {\bar{s}}\), \({\bar{c}}(s)=\beta (\pi -v_0)-(1-\alpha \delta )s\le 0\), and hence, there is no participation, \(X=0\).
Second, we show that \(Y=0\) for \(s<{\underline{s}}\). Recall that in equilibrium, \(Y>0\) only if \(J\ge s_F\), where
Substituting the value of \(\lambda ^*\) into (A.9), after some manipulations, yields:
Next, substituting \(p(\lambda ^*)\) into the expression for J, after some manipulations, yields:
At last, solving inequality \(J\ge s_F\) for s yields:
\(\square \)
1.3 Proof of Lemma 4
Lemma 4
For all \(s\in [{\underline{s}},\beta (\pi -u_0)]\), the welfare in the model with moral hazard is equal to:
and it is strictly increasing in s.
For all \(s\in (0,{\bar{s}})\), the welfare in the benchmark model is equal to:
and it is strictly decreasing in s.
Let us calculate the welfare in the benchmark model first. In every period, an individual of type \(c<{\bar{c}}(s)\equiv \beta (\pi -v_0)-(1-\alpha \delta )s\) obtains \(w-c\). Also, with probability \(1-\alpha \), she is unemployed at the beginning of the period, so she pays search cost s. Thus, the lifetime utility of an individual of type \(c<{\bar{c}}(s)\) is equal to:
where we used that in equilibrium the wage satisfies \(w=u_0+\beta (\pi -u_0)\). The lifetime utility of an individual of type \(c\ge {\bar{c}}(s)\) is the unemployment income, \(u_0/(1-\delta )\). Hence, the consumer’s surplus (net of the unemployment income) is equal to:
Next, at the beginning of the period, the mass of firms who have a filled position is \(\alpha F({\bar{c}}(s))\). The lifetime utility of any such firm is \((\pi -w)/(1-\alpha \delta )\). Any firm that has an unfilled vacancy or inactive has zero lifetime utility. Hence, the producers’ surplus is equal to:
Summing up \(\overline{CS}(s)\) and \(\overline{PS}(s)\) gives the expression for welfare \({\overline{W}}(s)\). As \({\bar{c}}(s)\) is strictly decreasing in s, it is easy to verify that \(\overline{CS}(s)\) is strictly decreasing and \(\overline{PS}(s)\) is decreasing. Hence, \({\overline{W}}(s)\) is strictly decreasing.
Let us now calculate the welfare in the model with moral hazard. In every period, an individual of type \(c<c^*(s)\equiv \alpha \delta s\) obtains \(w-c\) and also pays search cost s with probability \(1-\alpha \) that she has become unemployed at the end of the previous period. Thus, the lifetime utility of an individual of type \(c<c^*(s)\equiv \alpha \delta s\) is equal to:
where we used that in equilibrium the wage satisfies \(w=u_0+s\). The lifetime utility of an individual of type \(c\ge c^*(s)\) is the unemployment income, \(u_0/(1-\delta )\). Hence, the consumer’s surplus (net of the unemployment income) is equal to:
Next, similarly to in the benchmark model, at the beginning of the period, the mass of firms who have a filled position is \(\alpha F(c^*(s))\). The lifetime utility of any such firm is \((\pi -w)/(1-\alpha \delta )\). Any firm that has an unfilled vacancy or inactive has zero lifetime utility. Hence, the producers’ surplus is equal to:
Summing up CS(s) and PS(s) gives the expression for welfare W(s). Taking the derivative of W(s) (where we have used \(dc^*(s)/ds=\alpha \delta \)) yields:
since by assumption \(s\le \beta (\pi -u_0)<\pi -u_0\) and \(\frac{1}{1-\delta }-\frac{1}{1-\alpha \delta }>0\). \(\square \)
Rights and permissions
About this article
Cite this article
Zapechelnyuk, A., Zultan, R. Job search costs and incentives. Econ Theory Bull 8, 181–202 (2020). https://doi.org/10.1007/s40505-019-00176-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40505-019-00176-2