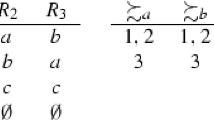Consistent Pareto improvement over the student-optimal stable mechanism

Abstract

We show that there is no consistent Pareto improvement over any stable mechanism. We introduce the following weakly consistent Pareto improvement (over the student-optimal stable matching) requirement: whenever a set of students, each of whom is assigned to a school that is underdemanded at the student-optimal stable matching, is removed with their assigned seats, then the assignments of the remaining students do not change. Our main result is that the efficiency-adjusted deferred acceptance mechanism (Kesten in Q J Econ 125(3):1297–1348, 2010) is the unique weakly consistent Pareto improvement over the student-optimal stable mechanism.

1 Introduction

The tradeoff between efficiency and stability has been a central question in the context of assigning students to schools following the pioneering work of Abdulkadiroğlu and Sönmez (2003). A matching is (Pareto) efficient if there is no other matching in which at least one student is better off and no student is worse off. Efficiency is attained, for example, by a serial dictatorship mechanism (Svensson 1999) or Gale’s top trading cycles mechanism (Shapley and Scarf 1974). On the other hand, stability requires that the matching is individually rational and there is no student–school pair who prefer each other to their current matches. The deferred acceptance algorithm (DA) of Gale and Shapley (1962) produces a stable matching. Furthermore, no mechanism can be both efficient and stable (Roth 1982). Kesten (2010) addresses the tradeoff between efficiency and stability by introducing EADAM, the Pareto of which improves over DA by allowing violation of some student priorities when these violations do not hurt the students.¹

Another desirable property of a mechanism is consistency (Thomson 1990), which states that when a group of students leaves the market with their assigned seats and the mechanism is applied to the reduced market, the assignment for the remaining agents should not change. Consistency can be thought of as a robustness check when students can trade their assigned seats using the same mechanism. It is known that DA is not consistent (Toda 2006; Afacan and Dur 2017). Our first result shows that no mechanism which Pareto improves over DA is consistent (Theorem 1). Since EADAM Pareto improves over DA, an implication of our result is that EADAM is not consistent (Corollary 1).²

Next, we provide a weaker consistency property. Given a matching, we say that a school is underdemanded at the given matching if no student strictly prefers it to his assigned school—underdemanded in the sense that no student prefers those schools to his assigned school. Using this concept, we introduce the following weak consistency property of a mechanism. Run a mechanism for a given market. Consider a subset of the students who are assigned by this mechanism to schools that are underdemanded at the DA outcome. This mechanism is weakly consistent (w.r.t. DA) if removing these students with their assigned seats and applying the mechanism to the reduced market do not change the assignments of the remaining students.³ We take DA as a benchmark and look for Pareto improvements. Since any school that is underdemanded at DA remains underdemanded at any Pareto improvement, and any student who is assigned to an underdemanded school at DA remains assigned to the same school at any Pareto improvement (Tang and Yu 2014, Lemma 1), the requirement that we only remove a set of students, each of whom is assigned to a school that is underdemanded at DA, makes sense, as these schools remain underdemanded for any mechanism that we consider. In other words, the match between a student and an underdemanded school at DA is an irrelevant match, since the same match happens at any Pareto improvement over DA, and such a mechanism should operate independently from these irrelevant matches.

Let us call a mechanism a weakly consistent Pareto improvement over DA, if it Pareto improves over DA and is weakly consistent w.r.t. DA. Our main finding is that EADAM is the unique weakly consistent Pareto improvement over DA (Theorem 2). The proof that any weakly consistent Pareto improvement must be EADAM follows from a simplified definition of EADAM proposed by Tang and Yu (2014). They show that EADAM can be produced as follows: Run DA once and identify underdemanded schools. Make the matches of underdemanded schools permanent and remove them from the market with the assigned students. Rerun this procedure until all students and schools are matched. Furthermore, Kesten (2010) proves that EADAM Pareto improves over DA. The more difficult part of the proof is showing that EADAM satisfies weak consistency w.r.t. DA. By the definition of EADAM, it is easy to see that if all students who are assigned to underdemanded schools at DA are removed with their assigned seats, then the matching for the remaining students does not change. However, it is not clear whether the assignments of the remaining students will change if some of the students, in particular only one, who are assigned to underdemanded schools at DA are removed with their assigned seats, which we establish in Appendix A. One implication of Theorem 2 is that DA is not weakly consistent w.r.t. itself.

Recently, EADAM has received attention in the literature (Dur et al. 2019; Troyan et al. 2018; Tang and Zhang 2017; Ehlers and Morrill 2017). These papers weaken stability and provide a different justification of EADAM. Instead, we introduce weak consistency and characterize EADAM as the unique weakly consistent Pareto improvement over DA.

Kesten (2010), Abdulkadiroğlu et al. (2009), and Alva and Manjunath (2019) show that there is no strategy-proof Pareto improvement over DA. We also study Pareto improvement over DA but instead of imposing strategy-proofness, we impose weak consistency and identify EADAM as the unique mechanism with these properties.

Other related literature includes Toda (2006), who characterizes the core of matching markets using consistency. Ergin (2002) shows that DA is consistent if, and only if, the capacity-priority structure satisfies acyclicity.⁴ In another recent paper, Afacan and Dur (2017) show that no stable mechanism is consistent.

2 Model

There exist a finite set of students, $\mathcal {S}$, and a finite set of schools, $\mathcal {C}$. Each student $s\in \mathcal {S}$ has a preference ranking$R_s$ over $\mathcal {C}\cup \{s\}$,⁵ where s represents an outside option for the student, which can be homeschooling, a private school, or the neighborhood school. The strict part of preference ranking $R_s$ is denoted by $P_s$, so if $c_1,c_2 \in \mathcal {C}\cup \{s\}$, $c_1\ne c_2$, and $c_1\mathrel {R_s}c_2$, then $c_1\mathrel {P_s}c_2$. School c is acceptable to student s if the student prefers it to the outside option, that is, $c\mathrel {P_s} s$. Each school $c\in \mathcal {C}$ has a capacity$q_c\in \mathbb {N}$, which is the maximum number of students that the school can admit, and a priority ranking$\succeq _c$ over the set of students and an empty seat, $\mathcal {S}\cup \{c\}$.⁶ Student s is acceptable to school c if the school ranks the student above the option of having an empty seat, i.e., $s\succeq _c c$.

The admission policy of school $c\in \mathcal {C}$ is represented by a choice rule$Ch_c: 2^{\mathcal {S}} \rightarrow 2^{\mathcal {S}}$, which maps each nonempty set $S \subseteq \mathcal {S}$ of students to a subset $Ch_c(S)\subseteq S$ of chosen students such that the number of chosen students does not exceed the capacity, that is, $|Ch_c(S)|\le q_c$. For each school $c\in \mathcal {C}$, $Ch_c$ is responsive to the priority ranking $\succeq _c$, i.e., for each $S \subseteq \mathcal {S}$, $Ch_c(S)$ is constructed by choosing the highest-priority acceptable students in S until $q_c$ students are chosen or no acceptable student is left.

A market is a tuple $(\mathcal {S},\mathcal {C},(R_s)_{s\in \mathcal {S}}, (q_c,\succeq _c)_{c\in \mathcal {C}})$. Sometimes, we fix the primitives of a market other than the student-preference relation profile $R\equiv (R_s)_{s\in \mathcal {S}}$ and the school-priority ranking profile $\succeq \equiv (\succeq _c)_{c\in \mathcal {C}}$. In this case, we call the pair $(R,\succeq )$ the market.

A matching $\mu$ is a function on the set of all agents such that

• for every student s, $\mu (s)\in \mathcal {C}\cup \{s\}$,

• for every school c, $\mu (c) \subseteq \mathcal {S}$ such that $\left| \mu (c) \right| \le q_c$, and

• for every student s and school c, $s\in \mu (c)$ if, and only if, $c=\mu (s)$.

In words, every student is matched to a school or unmatched, and every school is matched to a set of students that has a cardinality not greater than the capacity of the school. The last condition checks the feasibility of the matching so that a student is matched with a school if, and only if, the student is in the set that is matched with the school.

A matching $\mu$Pareto dominates a matching $\nu$ if every student s weakly prefers $\mu (s)$ to $\nu (s)$ and at least one student strictly prefers $\mu (s)$ to $\nu (s)$. A matching $\mu$ is Pareto efficient if it is not Pareto dominated.

A matching $\mu$ is stable if it satisfies the following two conditions.

• Individual rationality: for every student s, $\mu (s) \mathrel {R_s} s$, and for every school c, $Ch_c(\mu (c))=\mu (c)$, and

• No blocking: there exists no student–school pair (s, c) such that $c \mathrel {P_s} \mu (s)$ and $s\in Ch_c(\mu (c) \cup \{s\})$.

Individual rationality for a student means that the student’s match is weakly better than her outside option. For a school, it implies that the school would like to keep all its students. Since every school’s choice rule is responsive, this means that the number of students matched to a school is weakly smaller than its capacity and that each student matched with the school is acceptable to it. No blocking rules out the existence of a blocking student–school pair such that the student prefers the school to her assignment and the school finds the student acceptable and either it has an empty seat for the student or prefers the student to one of its assigned students.

The deferred acceptance algorithm of Gale and Shapley (1962) produces a stable matching. It has been used in different school districts to match students to schools.

Deferred Acceptance Algorithm (DA)

Step 1. Each student proposes to her top-ranked acceptable school. If there is no such school, then she is assigned to her outside option. Each school c considers the set of proposals that it receives, say $A_1(c)$. It tentatively accepts $Ch_c(A_1(c))$. It rejects all other proposals. If there is no rejection, then stop.

Step ${{\varvec{t}}}\ge {{\varvec{2}}}$. Each student who is rejected at Step $t-1$ proposes to her top-ranked acceptable school among the ones that have not rejected her yet. If there is no such school, then she is assigned to her outside option. Each school c considers the set of students that it tentatively accepted at Step $t-1$ together with students that have proposed at Step t, say $A_t(c)$. It tentatively accepts $Ch_c(A_t(c))$, and rejects other proposals. If there is no rejection, then stop.

DA produces the student-optimal stable matching for any market: this is the most preferred stable matching for all students (Gale and Shapley 1962). As a result, sometimes we refer to DA as the student-optimal stable mechanism. Even though the DA outcome is stable, it may not be Pareto efficient. To improve DA’s efficiency, Kesten (2010) provides another mechanism called efficiency-adjusted deferred acceptance mechanism (EADAM), which works by removing certain schools from the preference orderings of certain students and rerunning DA at the new market. Instead of providing Kesten’s original definition, we use a simplified version provided by Tang and Yu (2014).

Given a matching $\mu$, a school c is underdemanded at$\pmb {\mu }$ if no student s strictly prefers c to $\mu (s)$. The outside option of each student is also underdemanded.

Efficiency-Adjusted Deferred Acceptance Mechanism (EADAM)

Step 0. Run DA for the market $(R,\succeq )$.

Step ${{\varvec{t}}}\ge {{\varvec{1}}}$. Identify underdemanded schools at the outcome of Step $t-1$ of DA. Settle underdemanded schools with their matched students permanently. Remove these schools and students from the market. Stop if there are no remaining schools. Otherwise, run DA for the remaining market and move to the next step, Step $t+1$.

EADAM stops in finitely many steps and the outcome is Pareto efficient (Kesten 2010; Tang and Yu 2014).

We illustrate EADAM using the following example. We come back to this example in the next section.

Example 1

Let $\mathcal {S}=\{s_1,s_2,s_3\}$ and $\mathcal {C}=\{c_1,c_2,c_3\}$. Each school has capacity one. Let the student preferences and the school priorities be as follows.

At Step 0, we run DA. The outcome is $\{(s_1,c_3),(s_2,c_2),(s_3,c_1)\}$.

At Step 1, we first identify the underdemanded schools at the outcome of Step 0. Student $s_1$ prefers school $c_1$ to her matched school $c_3$. Student $s_3$ prefers school $c_2$ to her matched school $c_1$. Therefore, schools $c_1$ and $c_2$ are not underdemanded. However, no student prefers school $c_3$ to her assigned school, so school $c_3$ is underdemanded. Then, match school $c_3$ and student $s_1$ permanently and remove them from the market. Finally, we run DA for the remaining market and obtain $\{(s_2,c_1),(s_3,c_2)\}$.

At Step 2, we identify the underdemanded schools at the DA outcome of Step 1. Since both students get their top schools, both schools are underdemanded. We match these schools and students permanently. Since there are no schools remaining, we end the algorithm. The outcome is $\{(s_1,c_3),(s_2,c_1),(s_3,c_2)\}$.

A mechanism$\varphi$ takes a market $m=(\mathcal {S},\mathcal {C},(R_s)_{s\in \mathcal {S}}, (q_c,\succeq _c)_{c\in \mathcal {C}})$ as an input and produces a matching as an output. Given a market m, let $\varphi (m)$ denote the matching produced by mechanism $\varphi$ at market m. The outcomes for student s and school c produced by mechanism $\varphi$ at market m are denoted by $\varphi _s(m)$ and $\varphi _c(m)$, respectively. A mechanism is stable if it produces a stable matching at every market. A mechanism $\varphi$ is consistent if, for every market $m=(\mathcal {S},\mathcal {C},(R_s)_{s\in \mathcal {S}}, (q_c,\succeq _c)_{c\in \mathcal {C}})$, set of students $S\subseteq \mathcal {S}$, and student $s'\in \mathcal {S}\setminus S$,

$$\begin{aligned} \varphi _{s'}(m)=\varphi _{s'}(\mathcal {S}\setminus S,\mathcal {C}, (R_s)_{s\in \mathcal {S}\setminus S}, (q_c-\left| \varphi _c(m)\cap S \right| ,\succeq _c)_{c\in \mathcal {C}})). \end{aligned}$$

In words, a mechanism is consistent whenever a set of students take their assigned seats under $\varphi$ and leave; the mechanism $\varphi$ keeps the matchings the same for the reduced market with the remaining students and schools with reduced capacities (Thomson 1990). That is, when some students leave with their assigned seats, the mechanism still delivers the same outcome for the remaining students. Consistency can be thought of as a robustness property when any subset of students can trade their assigned seats using the same mechanism.

3 Results

A mechanism $\varphi$Pareto improves over another mechanism $\varphi '$ if at each market m, either $\varphi (m)=\varphi '(m)$ or $\varphi (m)$ Pareto dominates $\varphi '(m)$.⁷ A mechanism $\varphi$ is a consistent Pareto improvement over mechanism $\varphi '$ if mechanism $\varphi$ is consistent and Pareto improves over mechanism $\varphi '$.

We show that no stable mechanism has a consistent Pareto improvement.

Theorem 1

No stable mechanism has a consistent Pareto improvement.

Proof

We prove a stronger result. We show that even on the domain of markets where all students are acceptable at each school, no stable mechanism has a consistent Pareto improvement. Let $\varphi$ be a stable mechanism. Suppose, for contradiction, that mechanism $\varphi '$ is a consistent Pareto improvement over $\varphi$. Since no stable mechanism is consistent (Afacan and Dur 2017),⁸$\varphi '$ is not stable. Therefore, there exists a market m such that $\varphi '(m)$ is not a stable matching. Since $\varphi '$ is a Pareto improvement over a stable mechanism, $\varphi '(m)$ is individually rational for all students. Likewise it is also individually rational for schools since schools find all students acceptable in this domain. Therefore, there exists a blocking pair for $\varphi '(m)$ in market m.

Suppose that there exists a student s who blocks with an empty seat at a school c, i.e., $c\mathrel {P_s}\varphi '_s(m)$, $|\varphi '_c(m)|<q_c$, and $s\mathrel {\succ _c} c$. Let $m'$ be the reduced market after all students except student s leave with their $\varphi '(m)$ assignments. Note that $m'$ includes only student s and at least one seat of school c. There is a unique stable matching in $m'$, which is $\varphi (m')$, such that student s is assigned to a school which he weakly prefers to school c. (In fact, s is assigned to the best school at which he is acceptable and there is an available seat.) Since mechanism $\varphi '$ is a Pareto improvement over $\varphi$, we have $\varphi '_s(m')\mathrel {R_s}c$. Then, $\varphi '_s(m')\ne \varphi '_s(m)$, contradicting consistency of $\varphi '$.

Suppose that there exists a student s who blocks with a school c without an empty seat, i.e., there exists a student $s'$ such that $c\mathrel {P_s}\varphi '_s(m)$, $\varphi '_{s'}(m)=c$, and $s\mathrel {\succ _c} s'$. Let $m'$ be the market after all the students except students s and $s'$ leave with their $\varphi '(m)$ assignments. Note that $m'$ includes only students s and $s'$ and at least one seat of school c. Since in $m'$, student s has the highest priority at c, in every stable matching, in particular in $\varphi (m')$, s is assigned to a school that he weakly prefers to school c. Since $\varphi '$ is a Pareto improvement over $\varphi$, we have $\varphi '_s(m')\mathrel {R_s}c$. Then $\varphi '_s(m')\ne \varphi '_s(m)$, contradicting consistency of $\varphi '$. $\square$

Theorem 1 can also be shown using Lemma 5.7 in Toda (2006). One immediate corollary is the following:

Corollary 1

EADAM is not consistent.

Theorem 1 also implies that some of the mechanisms considered in the literature are not consistent. For example, a mechanism considered is Gale’s top trading cycles mechanism when students use their DA assignments as their initial endowments. Another corollary is that this mechanism is also not consistent.

Even though consistency is a desirable property, it may be too strong for the robustness of a mechanism. Some students may not be able to renegotiate their assignments because they are matched with schools that are deemed undesirable. To this end, we weaken consistency by allowing only a subset of students to renegotiate. We formalize this idea as follows. A mechanism $\varphi$ is weakly consistent w.r.t. mechanism$\pmb {\varphi '}$ if, whenever a set of students, each of whom is assigned to a school that is underdemanded at $\varphi '$, leaves the market with their assigned seats under $\varphi$; the mechanism $\varphi$ keeps the assignments the same for the reduced market with the remaining students and schools with reduced capacities. More formally, for every market $m=(\mathcal {S},\mathcal {C},(R_s)_{s\in \mathcal {S}}, (q_c,\succeq _c)_{c\in \mathcal {C}})$, set of students $S\subseteq \mathcal {S}$ such that $\varphi _s(m)$ is underdemanded at $\varphi '(m)$ for every student $s\in S$, and student $s'\in \mathcal {S}\setminus S$,

$\varphi _{s'}(m)=\varphi _{s'}(\mathcal {S}\setminus S,\mathcal {C}, (R_s)_{s\in \mathcal {S}\setminus S}, (q_c-\left| \varphi _c(m)\cap S \right| ,\succeq _c)_{c\in \mathcal {C}}))$.

Note that, equivalently, a mechanism is weakly consistent w.r.t. $\varphi '$ if, whenever one student who is assigned to a school that is underdemanded at $\varphi '$ leaves the market with his assigned seat, i.e., whenever the student is removed from the market and the capacity of his assigned school is reduced by one, the assignments of the remaining students do not change.

A mechanism $\varphi$ is a weakly consistent Pareto improvement over mechanism $\varphi '$ if mechanism $\varphi$ Pareto improves over mechanism $\varphi '$ and is weakly consistent w.r.t. $\varphi '$.

Our main result provides a characterization of EADAM using weak consistency.

Theorem 2

EADAM is the only weakly consistent Pareto improvement over DA.

Theorem 2 implies that DA is not weakly consistent w.r.t. itself, since DA Pareto improves over itself. Every consistent mechanism is also weakly consistent w.r.t. DA, and, therefore, the well-known Boston mechanism is weakly consistent w.r.t. DA but does not Pareto improve over DA.⁹ On the other hand, Gale’s top trading cycles mechanism, when students use their DA assignments as their initial endowments, Pareto improves over DA, but it is not weakly consistent w.r.t. DA.

The fact that EADAM is the only mechanism satisfying the two requirements follows easily by the definition of EADAM. The difficult part of the proof is to show that EADAM is weakly consistent w.r.t. DA. Again, by the definition of EADAM, it is easy to see that if all students who are assigned to underdemanded schools at DA are removed with their assigned seats, then the matching for the remaining students does not change. However, it is not clear whether the assignments of the remaining students will change if some of the students, in particular only one, who are assigned to underdemanded schools at DA are removed with their assigned seats. We provide the details of the proof in Appendix A.

Note that our weaking of consistency is w.r.t. DA. Alternatively, we can define weak consistency of a given mechanism w.r.t. the mechanism itself as follows. Run the mechanism and identify underdemanded schools at the outcome. Remove the underdemanded schools and their students from the market. Run the mechanism again. Then the outcome for the remaining agents should not change. The next example shows that EADAM is not weakly consistent w.r.t. EADAM, even though it is weakly consistent w.r.t. DA.

Example 2

Consider the setting in Example 1. The DA outcome for the original market is $\{(s_1,c_3),(s_2,c_2),(s_3,c_1)\}$. The only underdemanded school at DA is $c_3$. On the other hand, the EADAM outcome is $\{(s_1,c_3),(s_2,c_1),(s_3,c_2)\}$. If we remove school $c_3$ and its EADAM match student $s_1$ from the market and rerun EADAM, then we get $\{(s_2,c_1),(s_3,c_2)\}$. The outcome does not change for the remaining agents, which is an implication of weak consistency w.r.t. DA.

However, at EADAM outcome, there are two underdemanded schools: $c_2$ and $c_3$. If we remove school $c_2$ and its EADAM match student $s_3$ and run EADAM again, we get $\{(s_1,c_1),(s_2,c_3)\}$. The EADAM outcome for student $s_1$ changes in the reduced market. Therefore, this example also shows that EADAM does not satisfy the alternative consistency requirement that removing underdemanded schools and their assigned students at the mechanism should not change the outcome for the remaining agents. In other words, EADAM is not weakly consistent w.r.t. EADAM.

4 Conclusion

We have introduced a new axiom called weakly consistent Pareto improvement for matching markets. Using this axiom, we have provided a characterization of EADAM (Kesten 2010) as the unique weakly consistent Pareto improvement over DA.

Proof of Theorem 2

Step 0: Auxiliary notions and lemmas A well-known property of the DA mechanism, which we call weak monotonicity, will be useful. It requires the following. If some students leave the market with their DA assignments, i.e., if some students are removed from the market and the capacities of their DA schools are reduced accordingly, then all the remaining students are weakly better off in the new DA outcome. Weak monotonicity of DA is shown in Chen (2017) and called “weak consistency,” which is the terminology that we reserve for our new consistency notion.¹⁰

The following lemmas will be useful to prove our results. Lemma 1 is from Tang and Yu (2014).

Lemma 1

Consider a market m and the DA assignment for this market, DA(m). If DA(m) is Pareto dominated by another matching $\mu$, then each school c that is underdemanded in DA(m) is also underdemanded in matching $\mu$, and each student assigned to school c in DA(m) is also assigned to school c in matching $\mu$.

Lemma 2

Consider a market m and the DA assignment for this market, DA(m). Suppose that market $m'$ is obtained from market m by removing some students who are assigned to underdemanded schools in DA(m) together with their DA(m) assignments. Then each school c that is underdemanded in DA(m) is underdemanded also in DA$(m')$, and each student who is present in the market $m'$ and who is assigned to school c in DA(m) is assigned to c also in DA$(m')$.

Proof

Let S be the set of students who are removed, together with their assignments, to obtain market $m'$. By weak monotonicity, each student who is present in $m'$ weakly prefers his DA($m'$) assignment to his DA(m) assignment. Consider the matching $\mu$ obtained from DA($m'$) by adding S and their DA(m) assignments so that each student in S is matched to his DA(m) assignment at $\mu$, and, for the other students, $\mu$ agrees with DA($m'$). Then $\mu$ weakly Pareto dominates DA(m) and by Lemma 1, each school c that is underdemanded in DA(m) is underdemanded also in $\mu$ and each student assigned to school c in DA(m) is assigned to school c also in $\mu$.

Now, note that DA($m'$) can be obtained from matching $\mu$ by removing students in S with their assignments. Since the assignments of S are underdemanded at $\mu$, the set of underdemanded schools weakly expands, i.e., the set of underdemanded schools in $\mu$ is a subset of the set of underdemanded schools in DA($m'$). (It strictly expands if, at $\mu$, a school is demanded only by students in S). Hence, each school c that is underdemanded in DA(m) is also underdemanded in DA($m'$), and each student assigned to school c in DA(m) is also assigned to c in DA($m'$). $\square$

Lemma 3 states a new property of DA in a similar vein to weak monotonicity, although it is logically independent from weak monotonicity. The property requires that if more students with underdemanded seats leave a market with their DA assignments, then the DA outcome for every other student weakly improves. It does not imply weak monotonicity because it only focuses on the removal of students who are assigned to underdemanded schools. Also, the statement would not hold without the requirement that the removed students are assigned to underdemanded schools.

Lemma 3

Consider a market m with the set of students S and let $S''\subseteq S'\subseteq S$ be such that each student in $S'$ is assigned to an underdemanded school in DA(m). Then, each student in $S\setminus S'$ weakly prefers his DA assignment after the students in $S'$ leave with their DA(m) assignments to his DA assignment after the students in $S''$ leave with their DA(m) assignments.

Proof

Let m be the original market with students S, $m'$ be the market after the students in $S'$ leave with their DA assignments, and $m''$ be the market after the students in $S''$ leave with their DA assignments. Let DA(m), DA($m'$), and DA($m''$) denote the associated DA outcomes.

By weak monotonicity of DA, DA($m''$) weakly Pareto dominates DA(m) for the students in $S\setminus S''$. Since each student in $S'\setminus S''$ is assigned to an underdemanded school in DA(m), the assignments of the students in $S'\setminus S''$ are the same in DA($m''$) and in DA(m) by Lemma 1. Note that $m'$ can be obtained from $m''$ by removing the students in $S'\setminus S''$ together with their DA($m''$) assignments. Then, by weak monotonicity of DA, DA($m'$) weakly Pareto dominates DA($m''$) for the students in $S\setminus S'$. $\square$

Lemma 4

Consider a market m with the set of students S and let $S''\subseteq S'\subseteq S$ be such that each student in $S'$ is assigned to an underdemanded school in DA assignment. Let $m'$ be the market obtained from market m by removing the students in $S'$ together with their DA(m) assignments and let $m''$ be the market obtained from market m by removing the students in $S''$ together with their DA(m) assignments. Then, each school c that is underdemanded in DA($m''$) is underdemanded also in DA($m'$), and each student who is present in the market $m'$ and who is assigned to school c in DA($m''$) is assigned to school c also in DA($m'$).

Proof

By Lemma 2, each student in $S'\setminus S''$ is assigned to the same school in DA(m) and DA($m''$). Consider the matching $\mu$ obtained from DA($m'$) by adding $S'\setminus S''$ and their DA(m) assignments so that each student in $S'\setminus S''$ is matched to his DA(m) assignment at $\mu$ and, for the other students, $\mu$ agrees with DA($m'$). By Lemma 3, $\mu$ weakly Pareto dominates DA($m''$). Then, by Lemma 1, each school c that is underdemanded in DA($m''$) is underdemanded also in $\mu$ and each student assigned to c in DA($m''$) is assigned to c also in $\mu$.

Now, note that DA($m'$) can be obtained from $\mu$ by removing $S'\setminus S''$ with their assignments. Since the assignments of $S'\setminus S''$ are underdemanded at $\mu$, the set of underdemanded schools weakly expands, i.e., the set of underdemanded schools in $\mu$ is a subset of the set of underdemanded schools in DA($m'$). (It strictly expands if at $\mu$, a school is demanded only by students in $S'\setminus S''$.) Hence, each school c that is underdemanded in DA($m''$) is underdemanded also in DA($m'$), and each student who is present in $m'$ and who is assigned to c in DA($m''$) is assigned to c also in DA($m'$). $\square$

Step 1: EADAM is weakly consistent w.r.t. DA Consider an arbitrary market m with the EADAM outcome EADAM(m). Suppose that a student s whose EADAM(m) assignment is underdemanded in the student-optimal stable matching leaves the market with his EADAM(m) assignment, i.e., student s is removed and the capacity of his EADAM(m) assignment is decreased by one. Let us call this market $m'$ and the new EADAM outcome EADAM($m'$).

Since the EADAM(m) assignment of student s is underdemanded at the DA outcome, in the EADAM(m) student s must be permanently matched to and removed with his assignment in Round 1.

The following lemma will conclude that EADAM is weakly consistent w.r.t. DA.

Lemma 5

For each $r\ge 1$, each school c that is underdemanded in Round r of EADAM(m) is also underdemanded in Round r of EADAM($m'$) and the set of students assigned to school c in Round r of EADAM(m) and in Round r of EADAM($m'$) are the same, except that if school c is the EADAM(m) assignment of student s, student s is not assigned to school c in Round 1 of EADAM($m'$). Moreover, each school c that is underdemanded in Round r of EADAM($m'$) but not underdemanded in Round r of EADAM(m) is underdemanded in Round $r+1$ of EADAM(m), and the set of students assigned to school c in Round r of EADAM($m'$) and in Round $r+1$ of EADAM(m) are the same.

Proof

The proof is by induction on r. Note that the DA assignment in Round 1 of EADAM($m'$) can be obtained from the DA assignment in Round 1 of EADAM(m) by removing student s with his DA assignment in Round 1 of EADAM(m) and running DA with the remaining students and schools. By Lemma 2, each school c that is underdemanded in Round 1 of EADAM(m) is also underdemanded in Round 1 of EADAM($m'$) and the set of students assigned to c in Round 1 of EADAM(m) and in Round 1 of EADAM($m'$) are the same, except that if c is the EADAM(m) assignment of s, s is not assigned to c in Round 1 of EADAM($m'$).

Consider any school c that is underdemanded in Round 1 of EADAM($m'$) but not in Round 1 of EADAM(m). Note that the DA assignment in Round 2 of EADAM(m) can be obtained from the DA assignment in Round 1 of EADAM(m) by removing the students who are matched with underdemanded schools, including student s, with their assignments, and running DA with the remaining students and schools, while the DA assignment in Round 1 of EADAM($m'$) can be obtained from the DA assignment in Round 1 of EADAM(m) by removing only Student s with his assignment and running DA with the remaining students and schools. Then, by Lemma 4, each school c that is underdemanded in Round 1 of EADAM($m'$) is underdemanded in Round 2 of EADAM(m). In particular, each school c that is underdemanded in Round 1 of EADAM($m'$) but not underdemanded in Round 1 of EADAM(m) is underdemanded in Round 2 of EADAM(m), and since the students who are assigned to school c in Round 1 of EADAM(m) are present also in Round 2 of EADAM(m), we also have that the set of students assigned to c in Round 1 of EADAM($m'$) and in Round 2 of EADAM(m) are the same.

Suppose that the statement is true for each round before Round $r>1$. Note that, by the induction hypothesis, DA assignment in Round r of EADAM($m'$) can be obtained from DA assignment in Round r of EADAM(m) by removing the students who are matched with underdemanded schools in Round $r-1$ of EADAM($m'$) but not in Round $r-1$ of EADAM(m), together with their assignments, and re-running DA with the remaining students and schools. Then, by Lemma 2, each school c that is underdemanded in Round r of EADAM(m) is also underdemanded in Round r of EADAM($m'$), and the set of students assigned to c in Round r of EADAM(m) and in Round r of EADAM($m'$) are the same. Then, by Lemma 4, each school c that is underdemanded in Round r of EADAM($m'$) is underdemanded in Round $r+1$ of EADAM(m). In particular, each school c that is underdemanded in Round r of EADAM($m'$) but not underdemanded in Round r of EADAM(m) is underdemanded in Round $r+1$ of EADAM(m), and since the students who are assigned to school c in Round r of EADAM(m) are present also in Round $r+1$ of EADAM(m), we also have that the set of students assigned to c in Round r of EADAM($m'$) and in Round $r+1$ of EADAM(m) are the same. $\square$

By Lemma 5, it is clear that when student s leaves the market with his EADAM assignment, the EADAM assignments of the other students do not change.

Step 2: Any weakly consistent Pareto improvement over DA must be EADAM Consider an arbitrary market m. Let $\varphi$ be a weakly consistent Pareto improvement over the student optimal stable mechanism. By Lemma 1, all the students who are matched to an underdemanded school at DA(m) must be matched to the same schools, which are still underdemanded, at $\varphi (m)$.

Consider the market $m'$ obtained from market m after all the students who are matched to an underdemanded school at DA(m) are removed with their assigned seats. Note that the assignments of the removed students coincide with their assignment at EADAM(m). Now, by weak consistency of $\varphi$, the $\varphi (m)$ and $\varphi (m')$ assignments of the remaining students are the same. Again, by Lemma 1, all the students who are matched to an underdemanded school (underdemanded in the market $m'$) at DA($m'$) must be matched to the same schools, which are still underdemanded, at $\varphi (m')$. Then, consider the market $m''$ obtained from market $m'$ after all the students who are matched to an underdemanded school at DA($m'$) are removed with their assigned seats. Note that the assignments of the removed students coincide with their assignments at EADAM(m) (where they are matched at Round 2 of the EADAM(m)). Repeatedly applying the same arguments yields $\varphi (m)=$EADAM(m).