Skip to main content
SpringerLink
Log in

A comment on mixed oligopoly spatial model: the non-uniform consumer distribution

  • Research Article
  • Published:
Economic Theory Bulletin Aims and scope Submit manuscript

Abstract

We allow a general (non-uniform) consumer distribution in a mixed duopoly Hotelling model. We characterize respective conditions under which socially optimal pricing and location are achieved. We find that, while the condition for socially optimal pricing is fairly general, that for a socially optimal location is much more restrictive. Consequently, using a public firm to regulate a market may continue to yield a socially optimal price, but not the socially optimal location. This implies that privatization of the public firm may be desirable.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. Some other studies on mixed oligopoly use a different approach, such as mixed quantity duopoly model with endogenous timing (Amir and De Feo 2014), vertical differentiation model (Grilo 1994), and circular city model (Matsushima and Matsumura 2003).

  2. Other assumptions are the same as Cremer et al. (1991): \(x_1 \le x_2\), zero marginal cost, quadratic transport cost, and covered market.

  3. A general definition of \(\rho \)-concavity is provided in Caplin and Nalebuff (1991) p. 29. Our one-dimensional Hotelling model is a special case with \(\rho =-\frac{1}{2}\). Note that \(\rho \)-concave is a weaker condition than log-concave assumed in Anderson et al. (1997).

  4. The proof that T is quasi-convex in \(p_1\) can be done directly from the definition of quasi-convex. Details are available upon request.

  5. In C&N, the two firms’ objective functions (maximizing profit) are quasi-concave in firms’ own prices. In our model, both firms’ objective functions are still quasi-concave in their own prices, despite that the public firm maximizes welfare instead of its profit. Theorem 2 in C&N continues to hold in our case. One may write a proof similar to the proof of Theorem 2 in C&N. We leave this as an exercise to interesting readers.

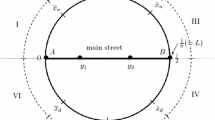
  6. This assumption is a quite common in location model, see Liu and Shuai (2013), and papers cited there. One exception is Anderson et al. (1997), in which consumer distribution is allowed be asymmetric. However, in Anderson et al. (1997), both firms are private firms, their objective functions are symmetric. In our mixed duopoly model, given firms are already asymmetric, introducing another asymmetry in consumer distribution will make the analysis too complex and is beyond the scope of this paper. Nevertheless, it is an interesting direction for future research.

  7. The proof are the same as Anderson et al. (1997), (section 5 on p. 123), and we skip it.

  8. The first inequality comes from the definition of \(\rho \)-concave and the first equality comes from the symmetry assumption.

  9. Liu and Shuai (2013) distinguish these two effects in a private duopoly model. Interesting readers may refer their paper for more details.

References

  • Amir, R., De Feo, G.: Endogenous timing in a mixed duopoly. Int. J. Game Theory 43(3), 629–658 (2014)

    Google Scholar 

  • Anderson, S.P., Goeree, J.K., Ramer, R.: Location, Location. Location. J. Econ. Theory 77(1), 102–127 (1997)

    Article  Google Scholar 

  • Caplin, A., Nalebuff, B.: Aggregation and Imperfect Competition: On the Existence of Equilibrium. Econometrica, 25–59 (1991)

  • Cardenas, O.J.: Mixed oligopoly and spatial agglomeration: a comment. Can. J. Econ. 40(1), 340–346 (2007)

    Article  Google Scholar 

  • Cremer, H., Marchand, M., Thisse, J.F.: Mixed oligopoly with differentiated products. Int. J. Ind. Organ. 9(1), 43–53 (1991)

    Article  Google Scholar 

  • Grilo, I.: Mixed duopoly under vertical differentiation. Ann. d’Economie et de Statistique 33, 91–112 (1994)

    Article  Google Scholar 

  • Inoue, T., Kamijo, Y., Tomaru, Y.: Interregional mixed duopoly. Reg. Sci. Urban Econ. 39(2), 233–242 (2009)

    Article  Google Scholar 

  • Kitahara, M., Matsumura, T.: Mixed duopoly. Product differentiation and competition. Manchester School 81(5), 730–744 (2013)

    Article  Google Scholar 

  • Liu, Q., Shuai, J.: Multi-dimensional product differentiation. Working paper (2013)

  • Matsumura, T., Matsushima, N.: Endogenous cost differentials between public and private enterprises: a mixed duopoly approach. Economica 71(284), 671–688 (2004)

    Article  Google Scholar 

  • Matsushima, N., Matsumura, T.: Mixed oligopoly and spatial agglomeration. Can. J. Econ. 36(1), 62–87 (2003)

    Article  Google Scholar 

  • Shuai, J.: Mixed duopoly with subcontracting. Manage. Decis. Econ. 37, 37–49 (2016)

    Article  Google Scholar 

  • Tabuchi, T., Thisse, J.F.: Asymmetric equilibria in spatial competition. Int. J. Ind. Organ. 13(2), 213–227 (1995)

    Article  Google Scholar 

Download references

Acknowledgments

We would like to thank the Editor (Nicholas Yannelis) and one anonymous referee whose comments improved this paper substantially.

Author information

Authors and Affiliations

  1. Wenlan School of Business, Zhongnan University of Economics and Law, 182 Nanhu Ave., East Lake High-tech Development Zone, 430073, Wuhan, People’s Republic of China

    Jie Shuai

Authors
  1. Jie Shuai
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jie Shuai.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Shuai, J. A comment on mixed oligopoly spatial model: the non-uniform consumer distribution. Econ Theory Bull 5, 57–63 (2017). https://doi.org/10.1007/s40505-016-0101-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40505-016-0101-4

Keywords

JEL Classification

Search

Navigation