A note on values for Markovian coalition processes

Abstract

The Shapley value is defined as the average marginal contribution of a player, taken over all possible ways to form the grand coalition $N$ when one starts from the empty coalition and adds players one by one. The authors have proposed in a previous paper an allocation scheme for a general model of coalition formation where the evolution of the coalition of active players is ruled by a Markov chain, and need not finish at the grand coalition. The aim of this note is to develop some explanations in the general context of time discrete stochastic processes, exhibit new properties of the model, correct some inaccuracies in the original paper, and give a new version of the axiomatization.

1 Introduction

The Shapley value is a well-known allocation scheme for both TU- and NTU-games with numerous applications. It is defined as the average marginal contribution of a player, taken over all possible ways to form the grand coalition $N$ when one starts from the empty coalition and adds players one by one.

In real situations, however, there is no a priori reason for a process of cooperation to end with the grand coalition, nor are all ways of forming the grand coalition necessarily feasible. This explains why the Shapley value can produce counterintuitive results in some cases, as pointed out by, e.g., (Roth 1980; Shafer 1980; Scafuri and Yannelis 1984).

Guided by these considerations, the authors have proposed an allocation scheme for a general model of coalition formation (Faigle and Grabisch 2012) where the evolution of the coalition of active players is ruled by a Markov chain. The classical Shapley value appears then as the particular case where the only transitions possible consist of the addition of a single player to the present coalition and all these transitions are equiprobable.

The aim of this note is to develop some explanations in the even more general context of time discrete stochastic processes that are not necessarily Markovian, exhibit new properties of the model and correct some inaccuracies in the original paper (Faigle and Grabisch 2012). In particular, we give a new version of the axiomatization. We restrict our exposition to the minimum, and refer the reader to the original paper for examples and further details on the Markovian model.

2 Coalition processes and values

We consider a finite set of players $N$, with $|N|=n$. By a scenario $\fancyscript{S}= S_0,S_1,S_2,\ldots$ we mean a sequence of coalitions $S_t\subseteq N$ starting with the empty set $S_0 =\emptyset$. No particular property is assumed on the sequence (there could be repetitions for example). In this note, however, we will restrict ourselves to scenarios of finite length. We call any two-element subsequence $S_t,S_{t+1}$ in $\fancyscript{S}$ a transition in $\fancyscript{S}$ and denote it by $S_t\rightarrow S_{t+1}$.

A scenario $\fancyscript{S}$ arises from the observation of the status of cooperation along (discrete) time $t=0,1,2,\ldots$. We assume that a process of cooperation among players in $N$ starts formally from the empty coalition $S_0=\emptyset$ (no player is active), then coalition $S_1$ is observed, then $S_2$, etc. Coalition $S_t$ is the set of active players (those engaged in cooperation or ready to cooperate) at time $t$. A finite scenario $\fancyscript{S}= S_0,S_1,\ldots , S_\tau$ is said to be of length $\tau$ with $S_\tau$ being the final state of cooperation. Note that we do not necessarily assume $S_\tau =N$.

Example 1

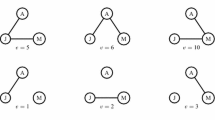
Letting $N=\{1,2,3,4\}$, consider the scenario

$$\begin{aligned} \fancyscript{S}= \emptyset , 1, 14, 1, 123, 34 \end{aligned}$$

with the convention that 123 denotes $\{1,2,3\}$, etc. At time $t=1$, player 1 becomes active and enters the current coalition. Then player 4 enters and is active at time $t=2$ but becomes inactive at time $t=3$ and leaves the current coalition. Next, the players 2 and 3 enter at the same time, while in the last time step $\tau =4$, 1 and 2 leave and 4 enters. So, players 3 and 4 finally cooperate while the other players abstain from the game.

The example illustrates how our model captures the original idea of Shapley and generalizes it (see Faigle and Grabisch 2012 for real examples from exchange economies of and Hart and Kurz 1983; Scafuri and Yannelis 1984).

We assume that scenarios are produced by some stochastic process, ruling the possible transitions between coalitions. In Faigle and Grabisch (2012), we have considered a Markov chain defined by a $2^n\times 2^n$ transition matrix $\mathbf U :=[u_{S,T}]_{S,T\subseteq N}$, where $u_{S,T}$ is the probability of the transition $S\rightarrow T$ to occur if $S$ is the currently active coalition. Therefore, the probability of a scenario $\fancyscript{S}=\emptyset ,S_1,\ldots , S_\tau$ to occur is simply

$$\begin{aligned} \mathrm Pr (\fancyscript{S}) = \prod _{k=1}^\tau u_{S_{i-1},S_i}, \end{aligned}$$

with $S_0=\emptyset$. In general, we have probability distributions $p^{t}$ on $2^N$ with $p^{t}(S)$ being the probability that $S$ is the active coalition at time $t$. $p^{t}$ can be viewed as the state of the coalition formation process at time $t$. Convergence to a limit state can be obtained by standard results in Markov chain theory.

We define an allocation scheme (value) for a general cooperation formation framework as follows. First, for any given scenario $\fancyscript{S}=\emptyset , S_1,\ldots , S_\tau$, we define what we call a scenario value, that is, an allocation scheme for the considered scenario: $\psi ^\fancyscript{S}:\mathcal G (N)\rightarrow \mathbb R ^n$, where $\mathcal G (N)$ is the set of TU-games on $N$. Then, the value $\psi$ is the family $(\psi ^{(\tau )})$ of the expectations of the scenario values at time $\tau$:

$$\begin{aligned} \psi ^{(\tau )} (v) = \sum _{\fancyscript{S}\in \mathfrak S _\tau }\mathrm {Pr} (\fancyscript{S})\psi ^\fancyscript{S}(v), \end{aligned}$$

where $\mathfrak S _\tau$ denotes the collection of all scenarios of length $\tau$. Therefore, it suffices to concentrate on the definition of a suitable scenario value. In Faigle and Grabisch (2012), we have introduced the so-called Shapley II value as follows.

Consider a scenario $\fancyscript{S}=\emptyset ,S_1,\ldots ,S_\tau$, and a particular transition $S_t\rightarrow S_{t+1}$ in $\fancyscript{S}$. The players in the symmetric difference $S_t\Delta S_{t+1} = (S_t\setminus S_{t+1})\cup (S_{t+1}\setminus S_t)$ are active at time $t$ in $S_t\rightarrow S_{t+1}$ as they either leave or enter the current coalition $S_t$. The Shapley II value for player $i$ is the sum of marginal contributions of $i$ in each transition where $i$ is active. We clarify this notion in more detail.

Suppose that $i\in S_t\Delta S_{t+1}$ is active. If $i$ is the only active player at time $t$, the marginal contribution is simply $v(S_{t+1})-v(S_t)$ because $i$’s activity causes this change in $v$. If $|S_t\Delta S_{t+1}| \ge 2$, the Shapley II value decomposes $S_t\rightarrow S_{t_+1}$ into elementary transitions (i.e., transitions such that only one player enters or leaves) and considers all possibilities of doing so. For example, the transition $2\rightarrow 13$, where player 2 leaves and players 1, 3 enter, can be decomposed into $3!=6$ different ways (so-called paths) corresponding to all permutations of players 1, 2, 3:

$$\begin{aligned}&2\rightarrow \emptyset \rightarrow 1\rightarrow 13\\&2\rightarrow \emptyset \rightarrow 3\rightarrow 13\\&2\rightarrow 12\rightarrow 1\rightarrow 13\\&2\rightarrow 12\rightarrow 123\rightarrow 13\\&2\rightarrow 23\rightarrow 3\rightarrow 13\\&2\rightarrow 23\rightarrow 123\rightarrow 13 \end{aligned}$$

In each path, the marginal contribution is computed as the difference $v(T^{\prime })-v(T)$, where $i$ is active in the elementary transition $T\rightarrow T^{\prime }$. For example, the marginal contribution of player 1 is $v(1)-v(\emptyset )$ in the first path, $v(13)-v(3)$ in the second, while the marginal contribution of player 2 is $v(\emptyset )-v(2)$ for these two paths. Averaging on all paths, we obtain the following marginal contributions for transition $1\rightarrow 23$:

$$\begin{aligned} \phi ^{1\rightarrow 23}_1(v)&= \frac{1}{6}v(1) + \frac{1}{3}(v(13)-v(3)) +\frac{1}{3}(v(12)-v(2)) + \frac{1}{6}(v(123)-v(23))\\ \phi ^{1\rightarrow 23}_2(v)&= -\frac{1}{3}v(2) + \frac{1}{6}(v(1)-v(12)) +\frac{1}{3}(v(13)-v(123)) + \frac{1}{6}(v(3)-v(23))\\ \phi ^{1\rightarrow 23}_3(v)&= \frac{1}{6}v(3) + \frac{1}{3}(v(13)-v(1)) +\frac{1}{6}(v(123)-v(12)) + \frac{1}{3}(v(23)-v(2)). \end{aligned}$$

In summary, the Shapley II scenario value is computed as follows:

$$\begin{aligned} \phi ^\fancyscript{S}_i(v) = \sum _{t\mid i\in S_t\Delta S_{t+1}}\phi ^{S_t\rightarrow S_{t+1}}_i(v) \end{aligned}$$

(1)

with

$$\begin{aligned} \phi ^{S_t\rightarrow S_{t+1}}_i(v) = \frac{1}{|S_t\Delta S_{t+1}|!}\sum _{\fancyscript{P} \text{ from } S_t \text{ to } S_{t+1}}(v(S^{\prime }_\fancyscript{P})-v(S_\fancyscript{P})) \end{aligned}$$

(2)

where “$\fancyscript{P} \text{ from } S \text{ to } T$” is any path from $S$ to $T$ in $2^N$, and $(S_\fancyscript{P},S^{\prime }_\fancyscript{P})$ is the unique edge (transition) of $\fancyscript{P}$ such that either $\{i\}=S_\fancyscript{P}\setminus S^{\prime }_\fancyscript{P}$ or $\{i\}= S^{\prime }_\fancyscript{P}\setminus S_\fancyscript{P}$.

Notice that the computation of the marginal contribution in a transition $S\rightarrow T$ resembles the computation of the classical Shapley value relative to the set $S\Delta T$ of active players. We formalize this idea. Consider a transition $S\rightarrow T$. It is convenient to introduce the mapping

$$\begin{aligned} \Gamma _{S,T}:S\Delta T\rightarrow \widehat{ST}, \quad K\mapsto K\Delta S, \end{aligned}$$

where $\widehat{ST}$ is the collection of sets in $S\cup T$ containing $S\cap T$ (observe that $K\Delta S$ always contains $S\cap T$). The inverse mapping $\Gamma ^{-1}:\widehat{ST}\rightarrow S\Delta T$ is simply $K\mapsto K\Delta S$ again, and we have a bijection between $S\Delta T$ and $\widehat{ST}$.

Next we introduce the local game $v_{S,T}$ on the set of active players $S\Delta T$, defined by

$$\begin{aligned} v_{S,T}(K) = v(\Gamma (K)) - v(S) = v(K\Delta S) - v(S), \quad K\subseteq S\Delta T. \end{aligned}$$

Also $v(K)=v_{S,T}(K\Delta S)+v(S)$ on $\widehat{ST}$.

Observe that if $i$ is entering, then we have $\{i\}=S^{\prime }_\fancyscript{P}\setminus S_\fancyscript{P}$ in the above notation. So the marginal contribution in $\phi ^{S\rightarrow T}_i$ is $v(S_\fancyscript{P}\cup i) - v(S_\fancyscript{P})$. Since $i\not \in S$, the marginal contribution is $v_{S,T}((S_\fancyscript{P}\Delta S)\cup i) - v_{S,T}(S_\fancyscript{P}\Delta S)$. If $i$ is leaving, the marginal contribution in $\phi ^{S\rightarrow T}_i$ is $v(S_\fancyscript{P}\setminus i) - v(S_\fancyscript{P})$. Since $i\in S$, however, the marginal contribution in terms of the local game is still $v_{S,T}((S_\fancyscript{P}\Delta S)\cup i) - v_{S,T}(S_\fancyscript{P}\Delta S)$, which is a term of the classical Shapley value of $i$ in $v_{S,T}$, denoted by $\phi ^\mathrm{Sh }_i(v_{S,T})$. Since $\Gamma$ is a bijection, the computation of $\phi ^{S\rightarrow T}_i(v)$ amounts to the computation of $\phi ^\mathrm{Sh }_i(v_{S,T})$. We have shown:

$$\begin{aligned} \phi ^{S\rightarrow T}(v) = \phi ^\mathrm{Sh }(v_{S,T}). \end{aligned}$$

(3)

where $\phi ^\mathrm{Sh }$ is the classical Shapley value.

3 Axiomatization of the Shapley II value

We denote by $\psi :\mathcal G \rightarrow \mathbb R ^{n\times \mathfrak S }$ a scenario value, where $\mathfrak S$ is the set of finite sequences of coalitions (not necessarily starting with $\emptyset$).

Two sequences $\fancyscript{S}=S_1,\ldots , S_q, \fancyscript{S}^{\prime }=S^{\prime }_1,\ldots , S^{\prime }_r$ are said to be concatenable if $S_q=S^{\prime }_1$, in which case their concatenation is the sequence

$$\begin{aligned} \fancyscript{S}\oplus \fancyscript{S}^{\prime } :=S_1,\ldots ,S_q,S^{\prime }_2,\ldots , S^{\prime }_r. \end{aligned}$$

Concatenation (C): Let $\fancyscript{S},\fancyscript{S}^{\prime }$ be two concatenable sequences. Then

$$\begin{aligned} \psi ^{\fancyscript{S}\oplus \fancyscript{S}^{\prime }} = \psi ^\fancyscript{S}+\psi ^{\fancyscript{S}^{\prime }}. \end{aligned}$$

Axiom (C) allows us to restrict our attention to transitions. Indeed,

$$\begin{aligned} \psi ^\fancyscript{S}= \sum _{k=0}^{t-1}\psi ^{S_k\rightarrow S_{k+1}} \end{aligned}$$

holds for every sequence $\fancyscript{S}=S_0,S_1,\ldots , S_t$.

Inactive players in transitions (IP): If $i$ is inactive in $S\rightarrow T$, then $\psi ^{S\rightarrow T}_i(v)=0$ for any game $v$.

Efficiency for transitions (E): For any transition $S\rightarrow T$ and game $v$, we have

$$\begin{aligned} \sum _{i\in N}\psi _i^{S\rightarrow T}(v) = v(T) - v(S). \end{aligned}$$

Linearity for transitions (L): $v\mapsto \psi ^{S\rightarrow T}(v)$ is a linear operator for any transition $S\rightarrow T$.

Symmetry for transitions (S): For any $i\in N$, any transition $S\rightarrow T$ and any permutation $\sigma$ on $N$, one has

$$\begin{aligned} \psi ^{S\rightarrow T}_i(v) = \psi ^{\sigma (S)\rightarrow \sigma (T)}_{\sigma (i)}(v\circ \sigma ^{-1}). \end{aligned}$$

We introduce the signature of a transition $S\rightarrow T$ as the parameter

$$\begin{aligned} \tau (S\rightarrow T) :=(|S\setminus T|,|T\setminus S|,|S\cap T|). \end{aligned}$$

As shown in Faigle and Grabisch (2012), the signature is invariant under permutations, and moreover, two scenarios are equal up to a permutation of the players if and only if they have the same signature.

$i\in N$ is a null player for $v$ if $v(S\cup i)=v(S)$ for all $S\subseteq N\setminus i$.

Null axiom for transitions (N): Every null player $i$ obtains $\psi _i^{S\rightarrow T}(v)=0$ relative to every transition $S\rightarrow T$.

Two players $i,j$ are antisymmetric if $v(K\cup \{i,j\}) = v(K)$ for every $K\subseteq N\setminus \{i,j\}$.

Antisymmetry for entering/leaving players (ASEL): If $i\in S\setminus T$ and $j\in T\setminus S$ are antisymmetric for $v$, then $\psi _i^{S\rightarrow T}(v) = \psi _j^{S\rightarrow T}(v)$.

Antisymmetric players have in some sense a counterbalancing effect: they annihilate each other when entering together a coalition, which can be interpreted by saying that they bring the same contribution but of opposite sign. Therefore, if one is leaving and the other entering, their contribution in the scenario becomes equal and of same sign.

Theorem 1

A scenario value satisfies (C), (L), (IP), (E), (S), (N) and (ASEL) if and only if it is the Shapley II scenario value (see Proof in Appendix).

An important point to note is that, in contrast to the classical case, two symmetry axioms are present. Relative to the transition $S\rightarrow T$, the first one, axiom (S), says that set of players can be freely permuted provided they all belong to one of the groups $S\setminus T$, $T\setminus S$, $S\cap T$, or $N\setminus (S\cup T)$. Now (IP) implies that we do not have to bother about players in $S\cap T$ and $N\setminus (S\cup T)$. The second symmetry axiom (ASEL) tells us how to exchange players between $S\setminus T$ and $T\setminus S$. Interestingly, however, both axioms can be deduced from the application of the classical symmetry axiom to the local game $v_{S,T}$. Indeed, consider two symmetric players $i,j\in S\Delta T$ for $v_{S,T}$, i.e., $v_{S,T}(K\cup i)=v_{S,T}(K\cup j)$ holds for any $K\subseteq (S\Delta T)\setminus \{i,j\}$. In the case $i,j\in S\setminus T$, this yields

$$\begin{aligned} v((K\Delta S)\setminus i) = v((K\Delta S)\setminus j), \end{aligned}$$

or, setting $K^{\prime }=(K\Delta S)\setminus \{i,j\}$, $v(K^{\prime }\cup i)=v(K^{\prime }\cup j)$, which means symmetry of $i,j$ for $v$ for sets in $\widehat{ST}\setminus \{i,j\}$. If $i,j\in T\setminus S$, we have

$$\begin{aligned} v((K\Delta S)\cup i) = v((K\Delta S)\cup j) \end{aligned}$$

which also exhibits symmetry of $i,j$ for those sets. In the case $i\in S\setminus T$ and $j\in T\setminus S$, we obtain

$$\begin{aligned} v((K\Delta S)\setminus i) = v((K\Delta S)\cup j), \end{aligned}$$

or, setting $K^{\prime }=(K\Delta S)\setminus i$, $v(K^{\prime })=v(K^{\prime }\cup \{i,j\})$, for every $K^{\prime }\subseteq \widehat{ST}\setminus \{i,j\}$. But this is precisely antisymmetry.

In the original paper, antisymmetric players were defined as players $i,j$ satisfying

$$\begin{aligned} v(K\cup i) - v(K)&= v(K\cup \{i,j\}) - v(K\cup i)\\ v(K\cup j) - v(K)&= v(K\cup \{i,j\}) - v(K\cup j) \end{aligned}$$

for any $K\subseteq N\setminus i,j$. Then two such antisymmetric players $i,j$ satisfy $\psi ^{S\rightarrow T}_i(v)=-\psi ^{S\rightarrow T}_j(v)$ for any sequence $S\rightarrow T$ with $i\in S\setminus T$ and $j\in T\setminus S$. It can be checked that Shapley II does have this antisymmetric property. However, it is too weak to ensure uniqueness of the scenario value.

Another interesting property is the following one, which was not mentioned in Faigle and Grabisch (2012).

Changing Role (CR): For any $S,T\subseteq N$, for any $i\in N\setminus (S\cup T)$, and any game $v$, we have $\psi ^{S\cup i\rightarrow T}_i(v) = - \psi _i^{S\rightarrow T\cup i}(v)$.

Consider a transition $S\rightarrow T$ where player $i$ is not participating (i.e., $i\not \in S\cup T$). Suppose now that player $i$ joins $T$, that is, $i$ becomes an entering player in the transition $S\rightarrow T\cup i$, then $i$ is active in this transition and has some marginal contribution, say $\alpha$. In contrast, assume now that player $i$ joins $S$ and leaves during the transition, i.e., we consider the transition $S\cup i\rightarrow T$. Then $i$ is active in this transition and has some marginal contribution, say $\beta$. Note that $(S\cup i)\Delta T=S\Delta (T\cup i)$, which means that the set of active players is the same, only the rôle of $i$ has been switched from entering to leaving, and the rest is left unchanged. Under these conditions, axiom (CR) says that the marginal contributions of $i$ in these two transitions are opposite, i.e., $\beta =-\alpha$.

We claim that Shapley II satisfies (CR). To establish the claim, we consider a transition $S\rightarrow T$ with $S\cup T\ne N$, and $i\in N\setminus (S\cup T)$. We know that for any $v$

$$\begin{aligned} \phi _i^{S\rightarrow T\cup i}(v) = \phi ^\mathrm{Sh }_i(v_{S,T\cup i}), \quad \phi _i^{S\cup i\rightarrow T}(v) = \phi ^\mathrm{Sh }_i(v_{S\cup i,T}). \end{aligned}$$

Setting $\ell = |(S\cup i)\Delta T|=|S\Delta (T\cup i)$, $|K|=k$, we find:

$$\begin{aligned} \phi ^\mathrm{Sh }_i(v_{S\cup i,T})&= \sum _{K\subseteq ((S\cup i)\Delta T)\setminus i}\frac{(\ell -k-1)!k!}{\ell !}(v_{S\cup i,T}(K\cup i) - v_{S\cup i,T}(K)) \\&= \sum _{K\subseteq S\Delta T}\frac{(\ell -k-1)!k!}{\ell !}(v(K\Delta S) - v((K\Delta S)\cup i))\\ \phi ^\mathrm{Sh }_i(v_{S,T\cup i})&= \sum _{K\subseteq (S\Delta (T\cup i))\setminus i}\frac{(\ell -k-1)!k!}{\ell !}(v_{S,T\cup i}(K\cup i) - v_{S,T\cup i}(K)) \\&= \sum _{K\subseteq S\Delta T}\frac{(\ell -k-1)!k!}{\ell !}(v((K\Delta S)\cup i) - v(K\Delta S)), \end{aligned}$$

which proves the claim. However, it can be demonstrated that the axiomatization of Shapley II fails if (CR) replaces (ASEL).

Appendix: Proof of Theorem 1

$(\Leftarrow )$ We check that (ASEL) is satisfied by Shapley II, the rest is left to the reader. It suffices to establish the antisymmetry property for a transition $S\rightarrow T$. Let us argue that $i,j$ being antisymmetric for $v$ implies that $i,j$ are symmetric in the classical sense for $v_{S,T}$, i.e., $v_{S,T}(K\cup i)=v_{S,T}(K\cup j)$ holds for all $K$ in $S\Delta T\setminus \{i,j\}$. Indeed, this would yield $\phi ^{S\rightarrow T}_i(v)=\phi ^\mathrm{Sh }_i(v_{S,T})=\phi ^\mathrm{Sh }_j(v_{S,T})=\phi _j^{S\rightarrow T}(v)$, the desired result.

Now, $v(K\cup \{i,j\})=v(K)$ for any $K\subseteq \widehat{ST}\setminus \{i,j\}$ is equivalent to

$$\begin{aligned} v_{S,T}((K\Delta S)\cup \{i,j\}) = v_{S,T}(K\Delta S) \end{aligned}$$

or

$$\begin{aligned} v_{S,T}(K^{\prime }\cup j) = v_{S,T}(K^{\prime }\cup i) \end{aligned}$$

with $K^{\prime }=(K\Delta S)\setminus i$, which proves the claim.

$(\Rightarrow )$ Since (C) is satisfied, it suffices to derive an expression for transitions. Under (L), (S), (N), it is shown in Faigle and Grabisch (2012, Prop. 2) that the value takes the form:

$$\begin{aligned} \psi ^{S\rightarrow T}_i = {\left\{ \begin{array}{ll}\sum _{K\subseteq N\setminus i}a_{\tau (S\rightarrow T),\tau (S\rightarrow T|K\cup i)}(v(K\cup i) - v(K)), &{} \text{ if } i\in S\setminus T\\ \sum _{K\subseteq N\setminus i}b_{\tau (S\rightarrow T),\tau (S\rightarrow T|K\cup i)}(v(K\cup i) - v(K)), &{} \text{ if } i\in T\setminus S\\ 0, &{} \text{ otherwise, } \end{array}\right. } \end{aligned}$$

where $\tau (S\rightarrow T|K):=(|(S\setminus T)\cap K|,|(T\setminus S)\cap K|,|S\cap T\cap K|,|K\setminus (S\cup T)|)$, and $a_{\tau (S\rightarrow T),\tau (S\rightarrow T|K\cup i)}$ and $b_{\tau (S\rightarrow T),\tau (S\rightarrow T|K\cup i)}$ are real coefficients. Then axioms (IP) and (E) imply:

$$\begin{aligned} \sum _{i\in N}\psi ^{S\rightarrow T}_i(v)&= v(T) - v(S) \\&= \sum _{i\in S\setminus T}\sum _{K\subseteq N\setminus i}a_{\tau (S\rightarrow T),\tau (S\rightarrow T|K\cup i)}(v(K\cup i)-v(K))\\&+ \sum _{i\in T\setminus S}\sum _{K\subseteq N\setminus i}b_{\tau (S\rightarrow T),\tau (S\rightarrow T|K\cup i)}(v(K\cup i)-v(K))\\&= \sum _{K\subseteq N}v(K)\left( k_la_{\tau ,k_l,k_r,k_c,k_0} + k_rb_{\tau ,k_l,k_r,k_c,k_0}\right. \\&-\left. (l-k_l)a_{\tau ,k_l+1,k_r,k_c,k_0} - (r-k_r)b_{\tau ,k_l,k_r+1,k_c,k_0} \right) , \end{aligned}$$

with the following notations: $\tau (S\rightarrow T)=:\tau$, $|S\setminus T|=:l$, $|T\setminus S|=:r$, $|S\cap T|=:c$, $|K|=k$, $\tau (S\rightarrow T|K)=(k_l,k_r,k_c,k_0)$, with $k_l=|(S\setminus T)\cap K|$, $k_r=|(T\setminus S)\cap K|$, $k_c=|S\cap T\cap K|$, and $k_0=k-k_l-k_r-k_c=|K\setminus (S\cup T)|$. Let us drop also the subindex $\tau$ since it is present everywhere. This gives by identification:

$$\begin{aligned}&\!\!la_{l,0,c,0} - r b_{l,1,c,0} = -1\end{aligned}$$

(4)

$$\begin{aligned}&-la_{1,r,c,0} + rb_{0,r,c,0} = 1\end{aligned}$$

(5)

$$\begin{aligned}&k_la_{k_l,k_r,k_c,k_0} + k_rb_{k_l,k_r,k_c,k_0} -(l-k_l)a_{k_l+1,k_r,k_c,k_0}\nonumber \\&\quad - (r-k_r)b_{k_l,k_r+1,k_c,k_0} = 0,\quad \forall K\ne S,T. \end{aligned}$$

(6)

Note that $1\le k_l\le l$ for $a_{k_l,k_r,k_c,k_0}$, $1\le k_r\le r$ for $b_{k_l,k_r,k_c,k_0}$, and in (6) the configurations $(k_l,k_r,k_c,k_0)=(l,0,c,0)$ and $(0,r,c,0)$ are excluded.

1. Suppose that $S\subset T$ holds, i.e., $\tau =(0,t-s,s)$. Then $l=k_l=0$, $r=t-s$, $c=s$, and (4), (5) yield $b_{0,1,s,0}=\frac{1}{t-s}$ and $b_{0,r,s,0}=\frac{1}{t-s}$, and the remaining equations become:

$$\begin{aligned} k_rb_{0,k_r,k_c,k_0} - (r-k_r)b_{0,k_r+1,k_c,k_0} = 0,\quad \forall K\ne S,T. \end{aligned}$$

If $K\cap T\setminus S=\emptyset$, this reduces to

$$\begin{aligned} b_{0,1,k_c,k_0}=0,\quad \forall k_c,k_0 \end{aligned}$$

(7)

except the case $(k_c=s,k_0=0)$, which corresponds to $S$. Similarly, $K\supseteq T\setminus S$ yields

$$\begin{aligned} b_{0,t-s,k_c,k_0}=0, \quad \forall k_c,k_0, \end{aligned}$$

(8)

except in the case $(k_c=s,k_0=0)$, which corresponds to $T$.

So it remains to examine the case where all $K$ satisfy $K\cap (T\setminus S)\ne \emptyset$ and $K\not \supseteq T\setminus S$ (i.e., $0<k_r<t-s$). We prove by induction that $b_{0,k_r+1,k_c,k_0}=0$ holds for all $0<k_r<t-s$ and $k_c,k_0$, except for $k_c=s,k_0=0$, i.e., for $K=S\cup L$ with $\emptyset \ne L\subset T\setminus S$, where

$$\begin{aligned} b_{0,k_r+1,s,0}= \frac{k_r!}{(t-s)\cdots (t-s-k_r)}. \end{aligned}$$

For $k_r=1$, we have

$$\begin{aligned} b_{0,1,k_c,k_0} - (r-1)b_{0,2,k_c,k_0} =0. \end{aligned}$$

From (7) we get $b_{0,1,k_c,k_0}=0$ except if $(k_c=s,k_0=0)$, which entails $b_{0,2,k_c,k_0}=0$ for all $k_c,k_0$ except $b_{0,2,s,0}=\frac{1}{(t-s)(t-s-1)}$, the expected result. Assume that the assumption is true up to $k_r$ and compute the case $k_r+1$, assuming $k_r+1<t-s$. We find

$$\begin{aligned} (k_r+1)b_{0,k_r+1,k_c,k_0} - (r-k_r-1)b_{0,k_r+2,k_c,k_0} =0 \end{aligned}$$

By the assumption, the first term vanishes for all $k_c,k_0$, except for $k_c=s$ and $k_0=0$. This implies the second term to vanish except when

$$\begin{aligned} b_{0,k_r+2,s,0} = \frac{(k_r+1)!}{(t-s)\cdots (t-s-k_r)(t-s-k_r-1)}. \end{aligned}$$

Therefore, the expression of $\psi ^{S\rightarrow T}_i$ becomes

$$\begin{aligned} \psi ^{S\rightarrow T}_i(v) = \sum _{\begin{array}{c} K\supseteq S\\ K\subseteq T\setminus i \end{array}}\frac{(t-s-k_r-1)!k_r!}{(t-s)!}(v(K\cup i)-v(K)), \end{aligned}$$

which is the expression of the Shapley value for a game on the set $T\setminus S$.

2. The case $T\subset S$ is analyzed similarly.

3. It remains to settle the case where $S\setminus T\ne \emptyset$ and $T\setminus S\ne \emptyset$ hold. Take any $i\in S\setminus T$ and $j\in T\setminus S$ and suppose that they are antisymmetric for $v$, i.e., $v(K\cup \{i,j\})=v(K)$ for any $K\subseteq N\setminus \{i,j\}$. This yields

$$\begin{aligned} \psi _i^{S\rightarrow T}(v)&= \sum _{K\subseteq N\setminus i}a_{k_l+1,k_r,k_c,k_0}(v(K\cup i) - v(K))\\&= \sum _{\begin{array}{c} K\subseteq N\setminus i\\ K\ni j \end{array}}a_{k_l+1,k_r,k_c,k_0}(v(K\setminus j) - v(K))\\&+ \sum _{\begin{array}{c} K\subseteq N\setminus i\\ K\not \ni j \end{array}}a_{k_l+1,k_r,k_c,k_0}(v(K\cup i) - v(K))\\&= \sum _{K\subseteq N\setminus \{i,j\}}\left( v(K)(a_{k_l+1,k_r+1,k_c,k_0} - a_{k_l+1,k_r,k_c,k_0}) + v(K\cup i)a_{k_l+1,k_r,k_c,k_0} \right. \\&\left. + v(K\cup j)(-a_{k_l+1,k_r+1,k_c,k_o})\right) . \end{aligned}$$

Similarly,

$$\begin{aligned} \psi _j^{S\rightarrow T}(v)&= \sum _{\begin{array}{c} K\subseteq N\setminus j\\ K\ni i \end{array}}b_{k_l,k_r+1,k_c,k_0}(v(K\setminus i) - v(K))\\&+ \sum _{\begin{array}{c} K\subseteq N\setminus j\\ K\not \ni i \end{array}}b_{k_l,k_r+1,k_c,k_0}(v(K\cup j) - v(K))\\&= \sum _{K\subseteq N\setminus \{i,j\}}\left( v(K)(b_{k_l+1,k_r+1,k_c,k_0} \!-\! b_{k_l,k_r+1,k_c,k_0})\right. \\&\left. + v(K\cup i)(-b_{k_l+1,k_r+1,k_c,k_0}) + v(K\cup j)b_{k_l,k_r+1,k_c,k_o}\right) . \end{aligned}$$

Since $\psi _i^{S\rightarrow T}(v)=\psi _j^{S\rightarrow T}(v)$ for any such game we deduce the system

$$\begin{aligned} a_{k_l+1,k_r+1,k_c,k_0} - a_{k_l+1,k_r,k_c,k_0}&= b_{k_l+1,k_r+1,k_c,k_0} - b_{k_l,k_r+1,k_c,k_0}\\ a_{k_l+1,k_r,k_c,k_0}&= -b_{k_l+1,k_r+1,k_c,k_0}\\ a_{k_l+1,k_r+1,k_c,k_0}&= -b_{k_l,k_r+1,k_c,k_0}, \end{aligned}$$

for $0\le k_l\le l-1$, $0\le k_r\le r-1$, $0\le k_c\le c$, and $0\le k_0\le n-|S\cup T|$, with the above conventions. Remark that the first line is redundant. Substituting in (4), (5) we obtain

$$\begin{aligned} a_{l,0,c,0}=-\frac{1}{l+r},\quad a_{1,r,c,0}= -\frac{1}{l+r}. \end{aligned}$$

(9)

Substitution into (6) leads to

$$\begin{aligned} (k_l+r-k_r)a_{k_l,k_r,k_c,k_0} - (k_r+l-k_l)a_{k_l+1,k_r,k_c,k_0}=0 \end{aligned}$$

(10)

with the restriction $1\le k_l\le l-1$, $1\le k_r\le r-1$. For the remaining cases, we get:

$$\begin{aligned} -(l+k_r)a_{1,k_r,k_c,k_0} + (r-k_r)a_{1,k_r+1,k_c,k_0}&= 0 ,\quad k_l=0,\quad 0\le k_r\le r\end{aligned}$$

(11)

$$\begin{aligned} (k_l+r)a_{k_l,0,k_c,k_0} - (l-k_l)a_{k_l+1,0,k_c,k_0}&= 0, \quad 1\le k_l\le l-1,\quad k_r=0\qquad \quad \end{aligned}$$

(12)

$$\begin{aligned} k_la_{k_l,r,k_c,k_0} - (l-k_l+r)a_{k_l+1,r,k_c,k_0}&= 0, \quad 1\le k_l\le l-1,\quad k_r=r\qquad \quad \end{aligned}$$

(13)

$$\begin{aligned} (l+r-k_r)a_{l,k_r,k_c,k_0} - k_ra_{l,k_r-1,k_c,k_0}&= 0, \quad k_l=l,\quad 0\le k_r\le r, \end{aligned}$$

(14)

where in (11) the case $(k_r=r,k_c=c,k_0=0)$ is excluded, and in (14) the case $(k_r=0,k_c=c,k_0=0)$ is excluded.

We claim that all coefficients corresponding to $K\setminus (S\cup T)\ne \emptyset$ (i.e., $k_0> 0$) or $K\not \supseteq (S\cap T)$ (i.e., $k_c<c$) vanish. Suppose then that $k_0>0$ and $k_c<c$ is given. From (14) with $k_r=0$, we deduce $a_{l,0,k_c,k_0}=0$. Substitution in (12) with $k_l=l-1$ yields $a_{l-1,0,k_c,k_0}=0$. Successive application of (12), again with $k_l=l-2,\ldots ,1$, yields

$$\begin{aligned} a_{k_l,0,k_c,k_0}=0,\quad 1\le k_l\le l. \end{aligned}$$

Since $a_{l,0,k_c,k_0}$ is also present in (14) with $k_r=1$, we have $a_{l,1,k_c,k_0}=0$. Now, in (10), $a_{l,1,k_c,k_0}$ is present with $(k_l=l-1,k_r=1)$, which yields $a_{l-1,1,k_c,k_0}=0$. Applying again (10) with $k_l=l-2,\ldots ,1$ we deduce

$$\begin{aligned} a_{k_l,1,k_c,k_0}=0,\quad 1\le k_l\le l. \end{aligned}$$

$a_{l,1,k_c,k_0}$ is present also in (14) with $k_r=2$. Proceeding as above we get

$$\begin{aligned} a_{k_l,2,k_c,k_0}=0,\quad 1\le k_l\le l. \end{aligned}$$

This can be done until $k_r=r$ in (14), which gives $a_{l,r,k_c,k_0}=0$. Then (13) has to be used with $k_l=l-1$ and so on. This yields

$$\begin{aligned} a_{k_l,r,k_c,k_0}=0,\quad 1\le k_l\le l. \end{aligned}$$

In summary, $a_{k_l,k_r,k_c,k_0}=0$ holds for $1\le k_l\le l$, $0\le k_r\le r$, $0\le k_c<c$ and $0<k_0\le n-|S\cup T|$, and our claim is proved.

Substituting into (10) to (14), we find

$$\begin{aligned} (k_l+r-k_r)a_{k_l,k_r,c,0} - (k_r+l-k_l)a_{k_l+1,k_r,c,0}&= 0,\quad 1\le k_l\le l-1, 1\le k_r\le r-1\nonumber \\\end{aligned}$$

(15)

$$\begin{aligned} -(l+k_r)a_{1,k_r,c,0} + (r-k_r)a_{1,k_r+1,c,0}&= 0 ,\quad 0\le k_r\le r-1\end{aligned}$$

(16)

$$\begin{aligned} (k_l+r)a_{k_l,0,c,0} - (l-k_l)a_{k_l+1,0,c,0}&= 0, \quad 1\le k_l\le l-1\end{aligned}$$

(17)

$$\begin{aligned} k_la_{k_l,r,c,0} - (l-k_l+r)a_{k_l+1,r,c,0}&= 0, \quad 1\le k_l\le l-1\end{aligned}$$

(18)

$$\begin{aligned} (l+r-k_r)a_{l,k_r,c,0} - k_ra_{l,k_r-1,c,0}&= 0, \quad 1\le k_r\le r. \end{aligned}$$

(19)

Observe that the system (16) together with $a_{1,r,c,0}=-\frac{1}{l+r}$ is a triangular system of $r+1$ equations in $r+1$ variables $a_{1,0,c,0},\ldots ,a_{1,r,c,0}$. It has therefore a unique solution. The same observation applies to the systems (17) with $a_{l,0,c,0}=-\frac{1}{l+r}$, (18) with $a_{1,r,c,0}=-\frac{1}{l+r}$, and (19) with $a_{l,0,c,0}=-\frac{1}{l+r}$, which determines in a unique way the variables $a_{1,0,c,0},\ldots ,a_{l,0,c,0}$, $a_{1,r,c,0},\ldots ,a_{l,r,c,0}$, and $a_{l,0,c,0},\ldots ,a_{l,r,c,0}$, respectively.

Substituting into the system (15), we find a system of $(l-1)(r-1)$ equations in the $(l-1)(r-1)$ variables $a_{2,1,c,0},\ldots , a_{2,r-1,c,0},a_{3,1,c,0},\ldots ,a_{3,r-1,c,0},\ldots$, $a_{l-1,1,c,0},\ldots , a_{l-1,r-1,c,0}$, which is triangular and consequently has a unique solution. Since we know that the coefficients of the Shapley II scenario value satisfy (15) to (19), it is the unique solution.