Abstract
Introduction
Risk stratification tools provide valuable information to inform treatment decisions. Existing algorithms for patients with multiple myeloma (MM) were based on patients with newly diagnosed disease, and these have not been validated in the relapsed setting or in routine clinical practice. We developed a risk stratification algorithm (RSA) for patients with MM at initiation of second-line (2L) treatment, based on data from the Czech Registry of Monoclonal Gammopathies.
Methods
Predictors of overall survival (OS) at 2L treatment were identified using Cox proportional hazards models and backward selection. Risk scores were obtained by multiplying the hazard ratios for each predictor. The K-adaptive partitioning for survival (KAPS) algorithm defined four groups of stratification based on individual risk scores.
Results
Performance of the RSA was assessed using Nagelkerke’s R2 test and Harrell’s concordance index through Kaplan–Meier analysis of OS data. Prognostic groups were successfully defined based on real-world data. Use of a multiplicative score based on Cox modeling and KAPS to define cut-off values was effective.
Conclusion
Through innovative methods of risk assessment and collaboration between physicians and statisticians, the RSA was capable of stratifying patients at 2L treatment by survival expectations. This approach can be used to develop clinical decision-making tools in other disease areas to improve patient management.
Funding
Amgen Europe GmbH.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Defining the prognosis of patients with multiple myeloma (MM) is increasingly challenging, and validated prognostic tools are needed in MM to standardize risk stratification of patients and ultimately improve risk assessment. |
Existing algorithms for patients with MM are based on patients with newly diagnosed disease, and these have not been validated in the relapsed setting or in routine clinical practice. |
A risk stratification algorithm (RSA) has been developed for patients with MM at initiation of second-line (2L) treatment, based on data from the Czech Registry of Monoclonal Gammopathies. |
The RSA uses 16 predictors to stratify patients with MM at 2L treatment into four risk groups with profoundly different survival expectations. |
This approach can be used to develop clinical decision-making tools in other disease areas to improve patient management. |
Introduction
Statistical tools capable of predicting risk can provide valuable information for healthcare professionals and patients and can potentially lead to improved outcomes. Widely used examples that have influenced clinical practice include the Kattan prostate cancer nomogram [1], the PREDICT online assessment tool [2, 3], and disease activity indices for systemic lupus erythematosus (SLE) [4, 5]. Recently, a phase 3 trial has shown that a web-based risk assessment tool, which used patient-reported symptoms and was sent to the oncologist between scheduled visits, improved the rate of early detection of relapse in patients with lung cancer, which in turn led to significant increases in overall survival (OS) in patients who used the tool than in those who did not [6].
Assessing the risk of death and predicting survival outcomes for patients with complex diseases can be challenging. Multiple myeloma (MM) is a complex malignancy that is heterogeneous in prognosis, response to treatment, and drivers of disease progression [7, 8]; despite this, staging algorithms have been developed for patients with newly diagnosed MM, such as the International Staging System (ISS). Data from more than 5000 patients were analyzed using a survival tree model to produce the ISS, a three-group staging system. The ISS is based on levels of serum β-2 microglobulin (Sβ2M) and serum albumin [9]. In 2015, a revised ISS (R-ISS) was published that used additional factors, such as cytogenetic abnormalities (CA) and lactate dehydrogenase (LDH) levels, to define the extent of disease progression in patients with newly diagnosed MM [10]. The R-ISS used a Cox proportional hazards model and the K-adaptive partitioning for survival (KAPS) algorithm to define the thresholds associated with each of the three disease stages [10, 11].
Despite recent advances in treatment, almost all patients with newly diagnosed MM will relapse eventually [12, 13]. Prognostic information obtained during first-line (1L) treatment could influence prognosis and treatment decision-making when patients are entering second-line (2L) treatment [7]; indeed, it has been shown that the predictors of OS can change between the initiation of 1L and 2L treatments [14]. Therefore, the first relapse is an important time during which physicians need further evidence of patient frailty and disease severity.
To date, none of the staging algorithms for MM have been validated in the relapsed setting. Herein, we describe the approach taken and statistical methods employed to develop a risk stratification algorithm (RSA) specifically for patients with MM initiating 2L treatment, and we compare the performance of the RSA with that of existing MM staging algorithms.
Methods
Selection of a Suitable Data Source
The Czech Registry of Monoclonal Gammopathies (RMG) is one of the largest of its kind and contains data on a substantial number of patients with MM initiating 2L treatment [15], as well as mature OS data and information on a large number of parameters [15]. This RSA was developed using validated and quality-controlled data that were collected between May 2007 and April 2016. Informed consent was granted in the original study of the RMG [15]. The data in this study are based on a previously conducted study, and informed consent was granted in the original study. Each center contributing to the registry received approval by an Institutional Review Board/Independent Ethics Committee (IRB/IEC). Further information on the ethical approval is detailed in the original study.
Eligibility Criteria
The RSA included individuals aged ≥ 18 years who were given one or more doses of anti-myeloma treatment after first relapse. Eligibility for stem cell transplantation was not considered. Patients who died or were lost to follow-up before initiating 2L treatment were excluded from the analysis.
Development Strategy
Step 1: Selection of Candidate Predictors of OS at the Initiation of 2L Treatment
Predictors of OS (Table 1) were identified by literature analysis and by the findings from a conceptual model of MM progression, which was defined by a Delphi process involving leading experts in MM [16, 17].
Step 2: Defining Parameters to Reflect Clinical Relevance
Splitting predictors into categories can lead to the omission of important information [18]; non-categorical variables were treated as continuous whenever possible. Martingale residuals and restricted cubic splines were used to model the relationships between continuous variables and the risk of death. Fractional polynomials and restricted cubic splines were used to assess the shape of the associations between non-linear variables and risk of death. These methods provide more flexible descriptions of the non-linearity of continuous variables than other procedures [19]. Current literature does not contain data describing the shape of the relationships between prognostic factors and OS in patients with MM. Therefore, the form of the modeled associations between continuous variables and OS was reviewed by experts in MM to assess whether the shape of the relationships between prognostic factors and OS demonstrated clinically meaningful associations.
Step 3: Imputation of Missing Values
Missing data for all but one of the parameters (CA at diagnosis) were added through multiple imputation by chained equations (using MICE, a software package in R) to provide full data sets for all patients in the RMG [20, 21]. Given that data on CA are not routinely collected, a different imputation method was required that would allow the risk of death associated with not having CA data to be captured in the RSA. An indicator method was selected in which missing observations were set to a fixed value, and an extra dummy variable was added to indicate whether the value for that variable was missing. However, patients who were lost to follow-up and those who had not died after initiation of 2L treatment were censored, and dates of death were not estimated in the imputation.
Five data sets were generated from the relapsed/refractory population of the RMG using an imputation algorithm. The selected predictors and predictor effects on OS were generally similar across data sets; however, there is limited information in the literature on methods for pooling the results of (backward) predictor selection from multiple imputed data sets [22, 23]. Therefore, the third imputed data set was chosen at random and used for development of the optimized RSA.
Step 4: Selecting Independent Predictors of OS
Covariates that correlated strongly with other candidate predictors (Pearson’s correlation coefficient > 0.40) were excluded. Backward selection was used in combination with clinical judgement for accurate prognostic model building. Clinical judgement via a Delphi process was used to preselect predictors before backward selection and to validate the model [17]. Backward selection was then performed in which multivariable Cox regression models were fitted with OS as the dependent variable, with the predictors that emerged from Pearson’s test as independent variables. The Akaike information criterion was used to select parameters for the RSA; however, studies have demonstrated that automated statistical predictor selection can exclude parameters that are known to have a strong independent effect on survival [18]. To prevent the omission of key variables, a group of predictors with acknowledged links to survival in patients with MM was included in the model regardless of statistical significance (Table 1).
Step 5: Calculating Patient-Specific Risk Scores
Risk scores were calculated for each individual patient for each of the selected predictors. For categorical variables, the hazard ratio (HR) belonging to the patient-specific value was used; for continuous variables, the log HR (β) multiplied by the patient-specific value was used (exp[β × patient value]). The resulting predictor-specific risk scores were multiplied with each other to produce a total risk score for each patient. The resulting patient-specific total risk score is continuous and can be interpreted as the relative risk of death for a given patient compared with a theoretical patient who has the lowest predictor value for each parameter. It is of note that baseline hazards were not relied upon to derive the individual risk scores for the RSA.
Step 6: Defining Risk Stratification Using Patient-Specific Risk Score
A KAPS algorithm was used to define the risk score boundaries between groups that would provide statistically significantly differences in OS for the RSA [11].
Step 7: Measuring the Performance of Cox Models and Risk Stratification
Performance of the optimized RSA Cox model, and the ISS and R-ISS Cox models, when applied to the RMG data set, was assessed using Nagelkerke’s R2 test, Harrell’s concordance index (C-index), and integrated discriminations improvement (IDI) [24]. Given that the optimized RSA was derived from the same data set in which it was tested, results for Nagelkerke’s R2 test, the C-index and IDI data were adjusted for optimism by bootstrapping [25]; the ISS and R-ISS were developed using different data sets.
The RSA was designed to predict survival from the initiation of 2L treatment; therefore, the treatment regimen used after stratification was not considered as a predictor. We assumed that each patient would receive the best possible therapy, meaning that future treatment should not bias the association of the predictors with the outcome. This assumption should have been tested using marginal structural models; however, these were not feasible in the development data set. Nevertheless, based on the similar outcomes achieved by each regimen within risk groups, we believe that the assumption holds.
The optimized RSA, the ISS, and the R-ISS were evaluated in the RMG data set using Kaplan–Meier curves and HRs for OS from the initiation of 2L treatment. P values for statistical significance were obtained for HRs for OS and for comparisons of OS between groups using the log-rank test.
Results
Patients
The RMG contained data on 1418 eligible patients with MM who had begun 2L therapy. Details on prior therapy have been reported previously [26]. The longest duration of follow-up was 103 months, and the median follow-up (considering censoring for mortality) was 27.6 (95% confidence interval [CI] 25.1–30.1) months. Details of baseline characteristics of patients have been reported previously [26].
Identification and Coding of Candidate Predictors
Twenty-nine candidate predictors were identified by literature searches and by the conceptual model (Table 1). Parameters such as the presence of extramedullary disease or Eastern Cooperative Oncology Group performance status at the initiation of 2L treatment are categorical in nature and were treated as such in the RSA (Table 2). Our intention was that none of the continuous variables would be categorized or dichotomized in the optimized RSA, but this was considered to be inaccurate in some cases. For example, the measurement of LDH levels is subject to considerable variation among laboratories. Consequently, LDH could not be regarded as a continuous parameter and was treated as a binary variable for which the reference categories and high-risk categories were below and above the upper limit of normal, respectively. Analysis of the curves plotted to show the relationships between the remaining continuous variables and OS, using restricted cubic splines (Fig. 1), highlighted that some of the other continuous parameters could not be treated as such in the model. The plot for time to initiation of 2L treatment against OS (Fig. 1) appeared to show that risk of death initially increased as time to initiation of 2L treatment increased; this was counterintuitive, and expert opinion suggested that the spike in the curve was not clinically meaningful. To ensure that the HR associated with time to initiation of 2L treatment was clinically meaningful, this variable was dichotomized (> 24 months and ≥ 24 months). When serum calcium level was treated as a fully continuous variable, the slope for risk of death continued to rise into the normal range (2.20–2.75 mmol/L) (Fig. 1). Experts advised that this did not reflect clinical observations and that patients with calcium levels in this range would not be regarded as having an increased risk of death when initiating 2L treatment for MM. Calcium level was, therefore, dichotomized and described in terms of the presence or absence of hypercalcemia (defined as calcium levels > 2.75 mmol/L).
When measured at the initiation of 2L treatment, age and serum albumin both exhibited a linear relationship with risk of death (Fig. 1). However, bone marrow plasma cell count, thrombocyte count, and Sβ2M (both at diagnosis and at the initiation of 2L treatment, unless specified otherwise) exhibited a non-linear relationship (Fig. 1). Bone marrow plasma cell count proved difficult to evaluate non-linearly because values up to 10% were recorded as 0% in the data; therefore, linearity was assumed, and bone marrow plasma cell count was coded as fully continuous. We investigated the use of three- or four-knot restrictive cubic splines and fractional polynomials to define curve shapes that would allow HRs to be assigned for thrombocyte count and Sβ2M. Various fractional polynomial transformations of each variable (x) were considered, including xp in which p was set at − 2, − 1, − 0.5, 0 (i.e. log[x]), 0.5, 1, 2 or 3. The functional form for Sβ2M and thrombocyte count was chosen using a modified backward selection process that identified the transformation with the best fit to the data. Fractional polynomials gave the best fit from a clinical standpoint, and this method was used to define the curve shape for Sβ2M (p set at 2) and thrombocyte count (p set at − 0.5) (Electronic Supplementary Material [ESM] Fig. S1). When cubic splines were applied to Sβ2M level or thrombocyte count, a decline in risk was suggested for extreme values compared with elevated values (10 vs. 5–6 mg/L for Sβ2M; > 400 × 109 vs. 300 × 109 cells/L for thrombocyte count); however, the confidence intervals (CIs) indicated a high degree of uncertainty around the area of decline (Fig. 1).
The ultimate objective when developing the RSA was to create a tool that could be used in the clinical setting. The mathematical transformations required to derive the HRs for Sβ2M and thrombocyte count were deemed to be too complex for clinical use, and a more practical solution was sought. The curve shapes generated by the application of fractional polynomials featured distinct gradient and plateau regions. Based on these curve shapes, threshold values at which the risk of death remained constant could be defined using the devised variable methods (Fig. 2) [27]. The curve for Sβ2M suggested a threshold of approximately 5.5 mg/L (Fig. 2), which was consistent with the value used in the ISS and R-ISS, as well as with expert opinion [9, 10]. No such clinically established threshold exists for thrombocyte count, but risk of death appeared to plateau between 150 × 109 and 200 × 109 cells/L; any value above this range can be considered to be a normal count. Experts agreed that any value in the plateau region would be in line with clinical observations; therefore, to identify the optimum cut-off, Cox models were run with the threshold value set at various points within this range. The best fit was observed when the threshold level was 150 × 109 cells/L, and this value was used in the optimized RSA.
Shape of the association of Sβ2M (a, b) and thrombocyte count (c) with overall survival as used in calculating the risk score in the algorithm. Thrombocyte count was measured at initiation of 2L treatment at which the risk of death remains constant, based on curves derived from fractional polynomials
Independent Predictors of OS from the Initiation of 2L Treatment
Following elimination of parameters that correlated strongly with other candidate predictors in the model and a backward selection process, 16 independent predictors of OS (at initiation of 2L unless stated otherwise) were identified (Table 2). Of the variables that were pre-specified to be included in the RSA regardless of statistical significance (Table 1), only time to initiation of 2L treatment was forced into the model. The calculation formula to measure risk score is included in the Appendix in the ESM.
Cox Model Performance
The Nagelkerke’s R2 test score, which was adjusted for optimism, was 0.23 for the optimized RSA Cox model (possible scores range between 0 and 1), and the C-index was 0.72 (a perfectly discriminating model would have a score of 1; a good discriminating model would have a score of > 0.70) (Table 3) [28].
Comparison of RSA Cox Model with ISS and R-ISS
When analyzed in the RMG data set, the optimized RSA Cox model outperformed the ISS and R-ISS Cox models as measured by Nagelkerke’s R2 test and C-index. The scores in the Nagelkerke’s R2 test for the optimized RSA model (adjusted for optimism), R-ISS, and ISS (not adjusted for optimism) are described in Table 3; the C-indices were 0.72, 0.60, and 0.59, respectively (Table 3).
Comparison of RSA Stratification with that of Existing Risk Algorithms
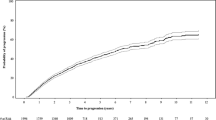
The performance of the RSA in the RMG data set was compared with that of the ISS and R-ISS (Fig. 3). Overlaps were observed in the 95% CIs for the HRs describing differences in OS between patients at each of the three ISS-defined disease stages, and a similar pattern was observed for the R-ISS. However, this was not the case with the RSA, despite the higher number of subgroups.
Discussion
We have developed an RSA that is capable of stratifying patients with MM who have relapsed and are initiating 2L treatment into four risk groups with distinct survival expectations. Multivariable modeling, coupled with guidance from leading experts in the field, was used to identify the strongest predictors of OS. Similar approaches were used to develop the Kattan prostate cancer nomogram [1], the PREDICT breast cancer tool [3], the SLE disease activity indices [4], and the R-ISS [10].
The RSA methodology differs from other risk assessment tools in the way that risk scores are calculated. In the RSA, risk scores are calculated by multiplying the HRs for each predictor; in comparison, the PREDICT tool, for example, calculates the prognostic index for each patient based on the sum of the weighted scores allocated to each of the predictors [3]. Multiplicative scoring is a more robust method for risk stratification than the commonly used predicted probabilities because the scores do not rely on the estimation of a baseline hazard. The baseline hazard often varies across populations, resulting in a low accuracy of risk stratification based on predicted probabilities [29, 30].
The RSA also uses a unique approach for stratifying patients. The R-ISS was developed using a KAPS algorithm to match patients with similar survival expectations with combinations of predictor variables [10]. In the RSA, KAPS was used to stratify individual patients according to their total multiplicative risk score, which allowed information on several parameters to be included and the granular nature of continuous variables to be captured.
Many algorithms categorize continuous variables, and this is the approach that was followed first; however, a body of evidence exists to suggest that the categorization of continuous variables can compromise the accuracy of predictive models [19, 31]. Treating the non-categorical parameters as fully continuous variables [1, 3] produced a more accurate picture of the drivers of disease progression for patients with MM initiating 2L treatment than a model in which all variables were categorized. However, some continuous predictors did not exhibit a linear relationship with risk of death, and HRs per unit for Sβ2M and thrombocyte count were derived after variables were transformed mathematically, and these were supported by expert opinion on the clinical appropriateness of the thresholds. Defining threshold values above which the HR remained constant provided the best balance of statistical accuracy and clinical utility. This approach allowed us to account for the plateaus in risk of death observed with variations in Sβ2 M concentration and thrombocyte count.
Missing values in the data set were handled through multiple imputation and the indicator method, enabling the algorithm to be used in patients for whom data for all predictive parameters were not available, including those for whom there were no CA data. In contrast, the R-ISS and many other staging and predictive algorithms are not designed to cope with missing data. In practice, many patients with MM do not get tested for high-risk CA and, as a result, cannot be staged using the R-ISS algorithm.
When assessed in patients with MM initiating 2L treatment, the Cox model developed for the optimized RSA performed better than the ISS or R-ISS Cox models, as measured using Nagelkerke’s R2 test, the C-index, and IDI. Furthermore, a Kaplan–Meier analysis of OS data from the initiation of 2L treatment illustrated that, in the Czech RMG data set, the optimized RSA stratified patients at first relapse, according to risk of death, more accurately than either the ISS or R-ISS.
The RSA methodology has some limitations. First, while backward selection is a common, validated method in prognostic model building, it is somewhat limited by the fact that all variables must be selected based on clinical significance, which can be generally challenging to assess. Second, further exploration is required to optimize predictor selection methods when analyzing multiple imputed data sets. Only one imputed data set, selected at random, was used, and this data set was employed to check for consistency in the other four data sets. Finally, the patient-specific scores were compared with those of a theoretical patient who had the lowest predictor value for each parameter. Future work could include measurement of the patient-specific score relative to normal laboratory values as baseline values.
Risk group definitions were derived using the KAPS algorithm only. A mechanism that factors in expert opinion when defining the boundaries among risk groups may enhance the clinical utility of the RSA. Comparisons between the performance of the optimized RSA and R-ISS were limited by the number of patients who were able to be evaluated using R-ISS; only 300 of the 1418 patients in the RMG initiating 2L treatment could be staged using the R-ISS owing to the lack of CA data. It must also be acknowledged that the comparison analysis between the optimized RSA and ISS and R-ISS has some limitations as, even though the ISS and R-ISS are often used in trials in relapsed/refractory setting, the ISS and R-ISS were not developed for 2L therapy and have previously not been validated in the relapsed setting.
The RSA was developed and tested using data from one country only (Czech Republic). Several factors are likely to cause regional variations in survival outcomes for patients with MM initiating 2L treatment. Indeed, real-world studies have shown that treatment patterns and outcomes for patients with MM vary across European countries [7, 32]; therefore, the tool has been validated using data sets from France, Germany and the UK in further studies (Hájek et al., in preparation).
Conclusions
In conclusion, we have developed an RSA to assess patients with MM at first relapse and to stratify them into groups with different survival expectations. Once fully validated, this algorithm may provide a framework to assist physicians with making treatment decisions according to survival expectations for patients with MM who are initiating 2L treatment. The methodology designed for the construction of this algorithm has the potential to have wide-reaching applications and could be used to create algorithms that predict risk in other diseases that influence survival.
References
Kattan MW, Eastham JA, Stapleton AM, et al. A preoperative nomogram for disease recurrence following radical prostatectomy for prostate cancer. J Natl Cancer Inst. 1998;90(10):766–71.
Ravdin PM, Siminoff LA, Davis GJ, et al. Computer program to assist in making decisions about adjuvant therapy for women with early breast cancer. J Clin Oncol. 2001;19(4):980–91.
Wishart GC, Azzato EM, Greenberg DC, et al. PREDICT: a new UK prognostic model that predicts survival following surgery for invasive breast cancer. Breast Cancer Res. 2010;12(1):R1.
Bombardier C, Gladman DD, Urowitz MB, et al. Derivation of the SLEDAI. A disease activity index for lupus patients. The Committee on Prognosis Studies in SLE. Arthritis Rheum. 1992;35(6):630–40.
Gladman D, Ginzler E, Goldsmith C, et al. Systemic lupus international collaborative clinics: development of a damage index in systemic lupus erythematosus. J Rheumatol. 1992;19(11):1820–1.
Denis F, Lethrosne C, Pourel N, et al. Improved overall survival in lung cancer patients using a webapplication-mediated follow-up compared to standard modalities: results of a phase III randomized trial. J Clin Oncol. 2016;34 Suppl:Abstr LBA9006.
Yong K, Delforge M, Driessen C, et al. Multiple myeloma: patient outcomes in real-world practice. Br J Haematol. 2016;175(2):252–64.
Moreau P, San Miguel J, Sonneveld P, et al. Multiple myeloma: ESMO clinical practice guidelines for diagnosis, treatment and follow-up. Ann Oncol. 2017;28[Suppl 4]:iv52–61.
Greipp PR, San Miguel J, Durie BG, et al. International staging system for multiple myeloma. J Clin Oncol. 2005;23(15):3412–20.
Palumbo A, Avet-Loiseau H, Oliva S, et al. Revised international staging system for multiple myeloma: a report from International Myeloma Working Group. J Clin Oncol. 2015;33(26):2863–9.
Eo S, Kang H, Hong S, et al. The K-adaptive partitioning for survival data, with an application to cancer staging 2014. https://arxiv.org/abs/1306.4615. Accessed Jul 2017
Hari P. Recent advances in understanding multiple myeloma. Hematol Oncol Stem Cell Ther. 2017;10(4):267–71.
Moreau P. The future of therapy for relapsed/refractory multiple myeloma: emerging agents and novel treatment strategies. Semin Hematol. 2012;49(Suppl 1):S33–46.
Hájek R, Jarkovsky J, Bouwmeester W, et al. Predictors of overall survival in patients with multiple myeloma initiating first- and second-line treatment in the Czech Republic. Blood. 2016;128:Abstr 3607.
Radocha J, Pour L, Spicka I, et al. Registry of monoclonal gammopathies (RMG) in the Czech Republic. Blood. 2015;126:Abstr 4514.
Gonzalez-McQuire S, Campioni M, Bennison C, et al. Development of a conceptual model of multiple myeloma for use in economic modelling: a systematic literature review to identify the evidence base. Value Health. 2015;18(7):A701.
Gonzalez-McQuire S, Dimopoulos MA, Weisel K, et al. Development of an initial conceptual model of multiple myeloma to support clinical and health economics decision making. MDM Policy Pract. 2019;4(1):2381468318814253. doi: https://doi.org/10.1177/2381468318814253.
Royston P, Moons KG, Altman DG, et al. Prognosis and prognostic research: developing a prognostic model. BMJ. 2009;338:b604. doi: https://doi.org/10.1136/bmj.b604.
Collins GS, Ogundimu EO, Cook JA, et al. Quantifying the impact of different approaches for handling continuous predictors on the performance of a prognostic model. Stat Med. 2016;35(23):4124–35.
White IR, Royston P. Imputing missing covariate values for the Cox model. Stat Med. 2009;28(15):1982–98.
van Buuren S, Groothuis-Oudshoorn K. MICE: multivariate imputation by chained equations in R. J Stat Softw. 2011;45(3):1–68.
Heymans MW, van Buuren S, Knol DL, et al. Variable selection under multiple imputation using the bootstrap in a prognostic study. BMC Med Res Methodol. 2007;7:33.
Wood AM, White IR, Royston P. How should variable selection be performed with multiply imputed data? Stat Med. 2008;27(17):3227–46.
Pickering JW, Endre ZH. New metrics for assessing diagnostic potential of candidate biomarkers. Clin J Am Soc Nephrol. 2012;7(8):1355–64.
Pavlou M, Ambler G, Seaman SR, et al. How to develop a more accurate risk prediction model when there are few events. BMJ. 2015;351:h3868.
Hájek R, Delforge M, Raab MS, et al. Development and validation of a novel risk stratification algorithm for relapsed multiple myeloma. Br J Haematol. 2019. https://doi.org/10.1111/bjh.16105.
Steyerberg E. Clinical prediction models. New York: Springer; 2009.
Harrell FE. Regression modeling strategies. New York: Springer; 2001.
Riley RD, Ensor J, Snell KI, et al. External validation of clinical prediction models using big datasets from e-health records or IPD meta-analysis: opportunities and challenges. BMJ. 2016;353:i3140.
Steyerberg EW, Vergouwe Y. Towards better clinical prediction models: seven steps for development and an ABCD for validation. Eur Heart J. 2014;35(29):1925–31.
Royston P, Altman DG, Sauerbrei W. Dichotomizing continuous predictors in multiple regression: a bad idea. Stat Med. 2006;25(1):127–41.
Raab MS, Cavo M, Delforge M, et al. Multiple myeloma: practice patterns across Europe. Br J Haematol. 2016;175(1):66–76.
Acknowledgements
Funding
Sponsorship for this study and the Rapid Service Fee were funded by Amgen Europe GmbH.
Medical Writing and Editorial Assistance
Editorial assistance in preparation for this article was provided by Sarah Petrig of Amgen, Zug, Switzerland. Medical writing support was provided by Matthew Long, PhD, of Oxford PharmaGenesis, Oxford, UK, and was funded by Amgen (Europe) GmbH. The Czech RMG provided the data for analysis in the current study.
Authorship
All named authors meet the International Committee of Medical Journal Editors (ICMJE) criteria for authorship for this article, take responsibility for the integrity of the work as a whole, and have given their approval for this version to be published.
Authorship Contributions
SMG, LDC, and WB performed the research; SMG, LDC, and WB designed the research study; all authors analyzed the data; all authors contributed to writing the paper by providing guidance and comments on its content.
Disclosures
Walter Bouwmeester is an employee of Pharmerit International who received funding from Amgen to conduct this research. Andrew Briggs has received consultancy fees from Amgen in relation to the work reported here. Ben van Hout has received consulting fees from Amgen. Roman Hájek has received research funding from Amgen and Celgene, consultancy fees from Amgen, Celgene, and Takeda, and fees from Amgen, Bristol-Myers Squibb, and Janssen. Sebastian Gonzalez-McQuire is an employee of Amgen Europe and a stockholder in Amgen Inc. Marco Campioni is an employee of Amgen Ltd and a stockholder in Amgen Inc. Lucy DeCosta is an employee of Amgen Ltd and a stockholder in Amgen Inc. Lucie Brozova has nothing to disclose.
Compliance with Ethics Guidelines
The data in this study are based on a previously conducted study and informed consent has been granted in the original study. Each centre contributing to the registry received approval by an Institutional Review Board/Independent Ethics Committee (IRB/IEC). Further information on the ethical approval is detailed in the original study.
Data Availability
The datasets generated and analyzed during the current study are available from the corresponding author on reasonable request.
Open Access
This article is distributed under the terms of the Creative Commons Attribution-NonCommercial 4.0 International License (http://creativecommons.org/licenses/by-nc/4.0/), which permits any noncommercial use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Author information
Authors and Affiliations
Corresponding author
Additional information
Enhanced Digital Features
To view enhanced digital features for this article go to: https://doi.org/10.6084/m9.figshare.10028474.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
This article is published under an open access license. Please check the 'Copyright Information' section either on this page or in the PDF for details of this license and what re-use is permitted. If your intended use exceeds what is permitted by the license or if you are unable to locate the licence and re-use information, please contact the Rights and Permissions team.
About this article
Cite this article
Bouwmeester, W., Briggs, A., van Hout, B. et al. Methodology of a Novel Risk Stratification Algorithm for Patients with Multiple Myeloma in the Relapsed Setting. Oncol Ther 7, 141–157 (2019). https://doi.org/10.1007/s40487-019-00100-5
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40487-019-00100-5