Introduction

Suppose we want to estimate the prevalence of depression among people experiencing homelessness in a particular US city. How might we recruit study participants? We could go to places where people experiencing homelessness gather and attempt to recruit those we encounter. However, since people experiencing homelessness who gather at certain locations may be different from those who do not gather at those locations, this convenience sampling approach would yield an unrepresentative sample. Limited sample representativeness can negatively affect estimates generated for parameters of interest [1]. For example, perhaps people who are experiencing homelessness and depression are less likely to meet with others in public spaces; they would in turn be less likely to be recruited for our study, leading us to underestimate the prevalence of depression among people experiencing homelessness.

Sampling methods are broadly categorized as either probability-based methods or non-probability-based methods (i.e., convenience samples) [2]. The distinction is that in probability sampling, the probability any given individual in the population is included in the sample is known or can be estimated using information about the sampling process [2, 3.••]. Adjustment of selection probabilities enables probability sampling to generate representative samples and estimates [3.••].

Probability-based sampling methods (i.e., simple random sampling, stratified sampling, cluster sampling) require a defined target population where the population size is known or can be estimated [4]. For instance, simple random sampling is a probability-based approach where participants are randomly selected from a list—or sampling frame—of all members of the target population. Simple random sampling has a relatively straightforward design and statistical analyses. Cluster sampling starts from a list of clusters which are mutually exclusive and comprehensively cover all individuals in the population [5]. Because all members of the target population have an equal chance of being sampled, we can use the proportion of individuals in the sample who are depressed to estimate the proportion of individuals in the total population who are depressed. The analytic approach does not require a statistical correction for the sampling method and can provide unbiased estimates of parameters in the original population. In other words, if an estimation process was repeated multiple times, the average of the estimates would be equal to the parameter of interest. Yet for many populations—including people experiencing homelessness—generating a complete sampling frame is challenging and often elusive.

People experiencing homelessness are an example of a so-called hard-to-reach population. Because traditional probability-based methods are rarely feasible, these populations are often studied via convenience sampling. Because the probabilities of inclusion are unknown, no statistical corrections can be applied, so estimates generated from convenience samples cannot produce representative or generalizable estimates and therefore estimates should be interpreted carefully. More rigorous sampling methods are available for hard-to-reach populations.

In this paper, we briefly review the strengths and limitations of sampling methods for hard-to-reach populations and then focus on one of the most popular of these methods—respondent-driven-sampling (RDS)—to provide researcher guidance on when and how to implement RDS. The principal approaches of RDS are not new, yet they continue to evolve as they are applied across multiple disciplines and varied populations of interest [6.••].

What Makes Certain Populations Hard to Reach?

Hard-to-reach populations are underground communities whose members may be reluctant to self-identify and for whom no sampling frame is available or can be constructed [7]. Examples include people who inject drugs, men who have sex with men, and survivors of sex trafficking. These groups are difficult to identify and recruit due to their marginalized status, desire for anonymity, stigma associated with their identities or behaviors, and/or fear of legal repercussions. Hard-to-reach populations may be impossible to fully enumerate with even a hypothetical sampling frame. They frequently constitute a small proportion of the general population and are floating or socially “invisible,” for example, due to their experiences with social marginalization from engaging in stigmatized activities. Some may conceal their group identity or be unwilling to participate in research for various reasons, including mistrust of researchers, who are rarely members of the community under study [8].

There are other subgroups for whom sampling methods for “hard-to-reach” populations can be applicable (i.e., tourists, adolescents with limited access to healthcare, and gig-economy workers) [9–11]. While such populations do not experience the same social marginalization as traditional hard-to-reach groups, sampling frames are usually unavailable. For example, though companies have rosters of gig workers, they may be reluctant to share these rosters with researchers.

Sampling Hard-to-Reach Populations

Effective sampling requires preliminary knowledge about the target population. This information is even more critical when working with hard-to-reach populations. Developing partnerships with community organizations and relationships within the target population can facilitate sampling and ultimately strengthen research quality. For example, community partners can introduce researchers to well-connected members of the target population to serve as initial participants or aid rapport-building to increase the likelihood of people participating in the study. Researchers can deepen their contextual knowledge about their populations of interest by conducting qualitative and ethnographic studies and working with a community advisory board [12]. It is important to plan for extended timelines and higher budgets when conducting research with hard-to-reach populations to accommodate community-engagement activities [13].

Common methods for sampling hard-to-reach populations include non-probability-based approaches (e.g., convenience sampling, snowball sampling) and probability-based approaches (e.g., time-location sampling [TLS], respondent-driven sampling) (Table 1) [14, 15].

Table 1 Methods for sampling hard-to-reach populations
Full size table

Non-probability-Based Approaches

Convenience Sampling

In convenience sampling, the most accessible individuals are selected into the study based on non-random criteria (e.g., through social media advertisements or by flagging down individuals on a street corner) [16]. Each member of the target population often has a different probability of being chosen, which is unknown. Without knowing the probability of inclusion, it is impossible to correct for the fact that some types of individuals are more likely to be enrolled. The sample is not representative of the population [17]. Non-probability-based sampling methods can be valuable during exploratory or formative studies with unresearched populations. But samples generated by non-probability-based sampling methods have limited generalizability, and are thus not intended for hypothesis testing about a broader population [18]. However, such methods are sometimes mistakenly used as if they were based on a probability sample [19].

Snowball Sampling

Snowball sampling was originally used to study social network structures and later adopted by researchers for studies of hard-to-reach populations [20.••••, 21.••••]. This approach relies on peer referral: researchers select initial participants (called seeds) who recruit their peers, who then themselves recruit their peers, and so forth until the target sample size is reached or target demographics are achieved. Peer referral is appealing because the activity of recruitment is placed on members of the population, who presumably have a better understanding of the population than the researchers. Snowball sampling is most useful in formative research where the goal is to generate some information about an understudied population. However, the method has similar weaknesses as convenience sampling, namely its sampling is non-random and there is no ability to know how the study sample resembles the target population, leading to limited generalizability. The selection of initial seeds likely has a strong impact on the overall composition of the sample, it can be logistically challenging and time-consuming, and data obtained from snowball sampling is often mistakenly used as if based on a probability sample.

Probability-Based Approaches

Unlike non-probability sampling methods, probability-based sampling methods, such as simple random sampling, stratified sampling, and cluster sampling, aim to provide more generalizable estimates [2, 3.••]. This is facilitated by a structured sampling process, including having a sampling frame and—in the case of stratified sampling and cluster sampling, for example—statistical adjustment.

Alternative methods have been developed to approximate probability-based samples when no sampling frame is available. Time-location sampling (sometimes referred to as venue-day-time sampling or temporal spatial sampling) and RDS are probability-based approaches used in research with hard-to-reach populations. With these approaches, information collected from study participants about their venue attendance (in TLS) or social network size (in RDS) enables researchers to generate sampling weights and calculate homophily or the tendency of individuals to be associated with similar individuals. These weights are then applied during data analysis to correct for unequal sampling probabilities entailed by the non-random sampling design.

Time-Location Sampling

For TLS, researchers construct a sampling frame of venues where members of the population are known to congregate, and possible times (including day of the week and time of day) when congregating at the venues is possible. The researchers randomly select venues and then times from the list. Researchers then recruit members of the target population at the selected times and locations [22]. In contrast to cluster sampling, where individuals belong to only one cluster (e.g., inpatients clustered by hospital), in TLS, individuals may be found in more than one time-location combination. This flexibility is useful because individuals are often mobile and not necessarily constrained to any one group or location over time. For example, a TLS sampling frame of venues for people experiencing homelessness may include homeless shelters, public parks, specific city blocks, and facilities that provide services. The sampling strategy thus allows researchers to increase coverage of diverse individuals in the population, not just those people who access shelters.

As with cluster sampling, an important step in TLS is estimating the probability of inclusion in order for statistical analysis to apply weights. Because the sampling units are not mutually exclusive, estimation of the probabilities of inclusion often (though not always) includes self-reported information on frequency of venue attendance [23]. This assumes that all members of the target population visit known venues. If some members of the target population do not attend any venues in the sampling frame, then the sample loses representativeness. Insights from community partners before and during recruitment can improve the venue list and reduce potential selection bias.

Respondent-Driven Sampling

RDS is a peer-referral probability-based sampling method developed in 1997 by Douglas Heckathorn via a study of AIDS prevention among people who inject drugs [24.••••]. Another early application of RDS was among jazz musicians in New York City [25]. RDS, like snowball sampling, begins with a small convenience sample of the population of interest, and participants then refer peers into the study. However, unlike snowball sampling, each participant’s network size (called degree) is recorded to facilitate estimation of probabilities of inclusion. An RDS sample can thus be weighted to be representative of the target population, under certain assumptions discussed in the subsequent section [26]. Also unlike snowball sampling, RDS participants use coupons to recruit their peers, which enables researchers to track social ties and assess the extent to which recruiters are recruiting people who are similar to themselves. Each recruiter is given a fixed number of coupons so that the final sample is not biased towards the most popular or connected members of the network.

In deciding between TLS and RDS, researchers should consider the target population’s characteristics: specifically, do members congregate at known locations, or are their social behaviors less visible? [27] If there are no identifiable places where the population of interest congregates and/or if most members of the population do not (at least sometimes) attend those venues, then TLS is not feasible. If the population is believed to be well-networked, RDS may be feasible and preferable to TLS in that it is more equipped to reach the most “hidden” members of the population. Several studies comparing TLS and RDS among men who have sex with men conclude that RDS reached more hidden sub-populations who were often at higher risk (e.g. lower socioeconomic status and non-gay-identifying) and achieved the sample faster and at lower cost [28–30].

Planning and Implementation

When implementing RDS, first evaluate whether the target population is sufficiently networked using formative research and community advisory boards [31]. Successful RDS recruitment requires that the target population must:

  • Consist of individuals who know one another as members of the target population;

  • Be adequately networked to accommodate the chain referral process; and

  • Be large relative to the study sample (given that respondents may only participate once and that each participant’s selection probability is assumed to remain constant over time) [32.••••, 33.••••].

Currently there is no consensus on how to plan sample size for an RDS study. One popular approach, similar to sample size estimation for simple random sampling, is to use a design effect. Design effects are adjustments that quantify the extent to which the expected under simple random sampling, typically resulting in larger sample sizes or wider confidence intervals than would be expected with simple random sampling [34]. For comparison, to estimate the sample size for an ordinary simple random sample, the sample size is multiplied by the hypothesized design effect. In a cluster randomized trial, the design effect is a function of cluster size and intracluster correlation (i.e., a measure of the relatedness of responses within a cluster) [5]. In RDS studies, a hypothesized design effect must be chosen rather than computed and the choice of design effect depends on the network structure in the population. A design effect of 2 is commonly used, such that the required sample size is twice that of a simple random sample [34, 35]. Some evidence indicates that 4 may be a more appropriate design effect for RDS studies [36]. Formative research can inform the choice of design effect.

Next, the research team selects seeds to initiate recruit recruitment. Careful seed selection takes time and may not be possible without formative research and collaboration with community members during RDS design [37]. Seeds are trained to recruit peers from their personal networks belonging to the target population. Successfully recruited individuals are in turn asked to recruit their peers and so forth. Individuals recruited by seeds represent a wave of recruitment. The first wave of recruits contacts their own network members and recruits a subsequent wave and so forth. When selecting initial seeds, researchers are encouraged to identify highly motivated, diverse, and well-connected individuals. All participants are monetarily compensated for study participation and for each peer they successfully recruit. Researchers usually limit the number of peer recruits per person (to three or four, sometimes fewer) to prevent people with larger social networks from dominating the sample.

During recruitment, researchers must track social ties and collect information on participants’ network sizes [38]. Researchers track social ties using paper or digital coupons with unique identification numbers (Fig. 1). Network size is generally measured using self-report. The phrasing of network size questions varies but specifies the population of interest, the type of contact, and some criterion on recency of contact. For example, “How many homeless individuals have you spoken to in-person in the last week?” One assumption of RDS is that recruits are selected at random from their network. Therefore, RDS estimators often rely on network size to derive sample weights for each participant. See the “Analysis” section for more information.

Fig. 1
figure 1

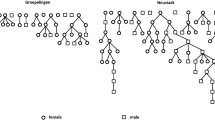
(a) Example of referral voucher to collect peer referral information. A unique coupon number is generated for each participant. (b) Example of recruitment chains resulting from respondent driven sampling, including examples of a likely health chain (originating from seed 1) and likely unhealthy chains (originating from seeds 2, 3, and 4)

Full size image

Also during recruitment, researchers should periodically monitor changes in the sample characteristics using data visualization (plotting cumulative prevalence of primary characteristic by time) to assess seed dependence. Seed dependence refers to the core RDS assumption that the final composition of the sample and inference about the population are minimally dependent on the initial selection of seeds. This concept of stable sample composition, or independence, is sometimes called equilibrium and is essential to the success of RDS in recruiting a representative sample [24.••••]. Nested in this concept is an assumption that homophily in social networks—the tendency of individuals to associate with similar individuals—is weak. A sufficiently large chain of waves will lead to a sample that is theoretically independent of the initial seeds; “sufficient” is defined not by the number of waves of recruitment but by whether the sample’s overall characteristics are still changing from one wave to the next. If the sample’s overall characteristics repeatedly shift from one wave to the next and have not yet stabilized, then more recruitment waves are required. Chain length—the number of waves resulting from a particular seed—often varies between seeds and there is no minimum number of waves required to reach equilibrium; however, consistently short recruitment chains across all seeds suggest that equilibrium has not been reached within the sample [17]. Choosing well-networked, diverse seeds and offering appropriate incentives for recruitment can mitigate issues related to seed dependence [4].

Gile, Johnston, and Salganik recommend assessing for seed dependence using three visualization techniques: convergence plots, bottleneck plots, and all points plots [32.••••]. Convergence plots depict the extent to which the estimate changes as more data are collected: visual evidence of the stabilizing of an estimate indicates lower dependence on initial seed selection. These plots however can mask differences between recruitment chains. As a result, bottleneck plots should also be used to depict dynamics of the estimates from each seed separately. Large differences in estimates between seeds suggest the presence of so-called bottlenecks (Fig. 1), in which populations divide into two or more subpopulations that have few ties with one another and may differ in their prevalence of specific traits. For example, if we included trait characteristics for recent drug use behaviors to Fig. 1 recruitment plot, then a bottleneck may be identified if all participants recruited by seed 2 reported not currently using drugs. RDS performs poorly in such populations because bottlenecks in the underlying social network can increase the effect of seed selection on the estimates, violating the assumption of seed independence [32.••••]. Recruitment chains may start at different times and grow at different speeds, factors that bottleneck plots do not account for; to address this, the all points plot plots unweighted characteristics of respondents by seed and sample order. Gile et al. (2014) [32.••••] recommend that researchers create these three plots for all traits of interest during data collection, even though there may be cases where the plots fail to detect problems.

Recruitment generally ends once the target sample size is reached and the researchers are satisfied with the extent of the sample’s equilibrium [24.••••]. If evidence of unstable estimates or bottlenecks is detected, more data should be collected, or researchers should consider using advanced estimators designed to correct for seed bias [48.••] or presenting estimates from each seed’s recruitment tree individually [39].

Analysis

Numerous methods for analyzing RDS data exist, relying on different sets of assumptions to draw inferences about the population. As described above, most, if not all, require assuming minimal seed dependence and minimal homophily and generally require information on the participants’ network size and the recruitment ties. For simplicity, we focus here on methods for producing univariate estimates, i.e., to describe characteristics of the target population. Multiple RDS estimators for this scenario exist, including RDS-I, RDS-II [40.••], and RDS-successive sampling (SS) [41], but there is no consensus on a single best approach.

RDS-II and RDS-SS estimators dominate the epidemiological literature. The RDS-II estimator leverages the assumption that probabilities of inclusion are proportional to network size and uses data smoothing to minimize potential effects of non-random recruitment. RDS-II performs particularly well when the sample size is much smaller than the population size [33.••••, 34, 42.••]. The RDS-SS estimator is similar to RDS-II but allows for the assumption of sampling with replacement (a consequence of the Markov process models that underlie RDS) to be ignored by correcting for the effect of finite populations. Because of this, the RDS-SS estimator requires an estimate of the total population size. It is not, however, very sensitive to differences in population size, so a rough approximation will usually produce reliable results [33.••••, 34, 42.••].

RDS Limitations, Optimism, and New Directions

As with any method, RDS has its share of limitations. Because RDS is dependent on network connections in the population of interest and relies on peer recruitment, issues with network connection can threaten sampling rigor. The assumption of random selection may be violated if recruited peers may be meaningfully different from nonrecruited peers. Second, selection bias can limit generalizability to the population of interest. Its implementation could have reached only certain segments of the population in a way that is difficult to assess and articulate.

Other challenges with RDS are that it is often difficult to estimate the size of the recruiter’s network (some solutions proposed in [43] [43]) and to estimate the refusal rate and associated potential impact of non-response bias. The basic question “how many people do you know?” suffers from transmission errors (i.e., when the respondent knows someone but is unaware that person belongs to the relevant subpopulation), barrier effects (i.e., when individuals know more or fewer members of a subpopulation than would be expected under random mixing), and recall problems (i.e., people tend to over-recall small subpopulations and under-recall large subpopulations) [44, 45].

Multiple analytic methods are available for univariate estimation and no consensus on a gold standard is established. Though the RDS-SS [43] method displays strong qualities, other methods have been proposed in recent years [42.••, 46]. Continued research is necessary to assess the performance of these methods. Further methodological research is also needed on bivariate or multivariate analysis for RDS data. Researchers have implemented various approaches, including survey-weighted analysis. Under the weighted approach, weights from univariate analysis are extracted and applied to the bivariate or multivariate, under the conventional survey-analysis approach. The analyses are often clustered by chain or recruiter. A recent study found that such approaches do not perform better than “naive” analyses in simulation studies; in fact, the naive analysis outperformed the survey-analysis approach [47.••]. It remains an open question however and there may be other methods that perform better than the naive analysis.

Despite concerns and challenges identified above, RDS remains a valuable tool for studying hard-to-reach populations. Although imperfect, RDS is often superior to other feasible options, such as convenience and snowball sampling. TLS implementations may be relatively easy to describe, but TLS excludes individuals who do not visit venues that are known to the researchers. A new hybrid approach capitalizes on the strengths of TLS and RDS, respectively [48.••], and may be useful for studying populations for whom conventional TLS and RDS do not work (because venues and networks are sparse) and for whom population-based survey methods are unfeasible. Starfish sampling includes random selection of venue-day-time units from a mapping of locations where the population can be found combined with short chains of peer referrals from their social networks at the venue. This more flexible design may have broader applicability for research in other hidden, hard-to-reach populations and in small populations that lack defined sample frames.

Continued research offers reasons for optimism regarding RDS. Studies have found robustness of RDS analysis to violations of assumptions, including assumptions regarding accurate reporting of network size [49]. Studies have also demonstrated robustness of analysis to the analytic method [41]. And, the finding that “naive” multivariate analysis of RDS data performs well eases anxiety regarding complexity of other analytic options. Increased uptake and discussion of RDS has led to more sophisticated use of the sampling method, beginning in the planning stage with formative assessments. Careful consideration is also required in interpreting and presenting RDS findings, with guidance from STROBE [50, 51].

Conclusions

Including historically underrepresented hard-to-reach populations in research is key to improving the representativeness and generalizability of findings and for informing effective interventions. All sampling methods are imperfect—including non-probability-based and probability-based sampling approaches. In some situations, however, TLS, RDS, or a combination may be appropriate for identifying and recruiting samples from diverse and hard-to-reach populations and offer important improvements over fully non-probability-based methods. Careful implementation of these methods will enhance their ability to produce unbiased estimates. This review is intended to inspire researchers in various disciplines to choose sampling methods prudently with respect to the target populations of interest, to expand researchers’ toolkits for sampling hard-to-reach populations, and to encourage investigators to expand their research questions to hard-to-reach populations.