Abstract
The experimental determination of stability lobe diagrams (SLDs) in milling can be realized by either continuously varying the spindle speed or by varying the depth of cut. In this paper, a method for combining both these methods along with an online chatter detection algorithm is proposed for efficient determination of SLDs. To accomplish this, communication between the machine control and chatter detection algorithm is established, and the machine axes are controlled to change the spindle speed or depth of cut. The efficiency of the proposed method is analyzed in this paper.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Material removal rate (MRR) significantly determines the financial viability of a cutting process. In the case of conventional as well as high-speed milling, MRR is mainly limited by the maximum achievable depth of cut without process instability or regenerative chatter. The critical depth of cut during milling can be either estimated by a simulation model or established experimentally for a given combination of machine, workpiece, and tool.
Milling simulation models for predicting instability have been the subject of extensive research in the past decades. The process of regenerative chatter for interrupted cutting, such as milling, where the cutting forces vary periodically, can be modeled using non-autonomous delay differential equations (DDEs). A time-domain numerical solution of these equations gives the stability boundaries as in Ref. [1]. Altintas and Budak [2] proposed a zeroth order approximation of the Fourier terms of the periodic cutting force coefficients. Subsequently, a complex analytical formulation of the relation for critical depth of cut was proposed in Refs. [3, 4]. Although these simulation models of the dynamic milling process are valid for tools with large numbers of teeth and high radial immersion, they still suffer from several disadvantages. Simulative methods require extensive measurement of the dynamics between the workpiece and tool in different directions. Furthermore, several assumption and simplifications regarding material properties, force characteristics, and dynamic behavior are necessary to create a dynamic milling model, which introduces inaccuracies. Despite these simplifications and assumptions, an analytical solution for the stability boundary still requires certain expertise and cannot be readily implemented in the industry.
Experimentally determined stability boundaries, on the other hand, represent the true boundaries and act as a reference for comparing the accuracy of analytical models. However, the experimental determination necessitates several cutting trials covering the variables of spindle speed and depth of cut. Each trial is conducted at a fixed spindle speed and depth of cut. This is a tedious and time-consuming job. In the literature, two methods have been proposed for expediting the experimental determination of stability borders: the continuous variation of depth of cut at constant spindle speed [5], and the continuous variation of spindle speed with constant depth of cut [6]. These correspond to movements along the vertical and horizontal axes in the stability lobe diagrams (SLDs) (see Fig. 1). Both these approaches require an online or real-time detection of the occurrence of instability.
Quintna et al. [5] used a microphone and a frequency-domain based chatter detection algorithm. However, as the detection is based on the fast Fourier transformation (FFT) of the sampled time period, there is always a delay associated with the sampling time period. Additionally, initial milling trails are required to identify the chatter frequency. The frequency-domain identification can be erroneous if the chatter frequency lies at the teeth engagement frequency. Grossi et al. [6] proposed a ramp-up test where the spindle speed was varied linearly, and the feed per tooth and depth of cut were kept constant. Here, as well, a frequency-domain based order analysis technique is used for chatter detection; however, it suffers from the same drawbacks mentioned previously. This paper proposes a time-domain based online chatter detection algorithm that does not suffer from significant time delays and disadvantages associated with frequency-domain methods.
A successive combination of both experimental strategies for reaching instability, along with an online, real time chatter detection algorithm, and a communication with the machine to affect a change in machining parameters would drastically reduce the experimental effort associated with establishing SLDs. This paper proposes such a method so that SLDs can be established rapidly (see Fig. 1). The paper is organized as follows: the online chatter detection algorithm based on the Poincaré map is discussed, together with the necessary signal processing required for achieving sharp trajectories of spindle displacements. Section 3 gives an overview of the measurement setup for combining experimental strategies. Section 4 presents a comparison of the stability boundaries obtained by the conventional method and by the proposed method. Conclusions are presented in Sect. 5.
2 Real time chatter detection algorithm
The online, time-domain chatter detection algorithm proposed in this paper is built on the approach of using Poincaré maps and sections as introduced by Davies et al. [7]. This method is based on vibration of the cutting tool in a two-dimensional plane. The trajectory of the displacement of the tool centerpoint (TCP) in this two-dimensional plane is plotted, and the TCP position at a given angle is sampled once per revolution. Hence, the trajectory is analogous to a Poincaré map and the once per revolution sampling is analogous to a Poincaré section. For a stable process, the motion of the TCP and hence the trajectory repeats itself. Upon the onset of chatter, the trajectory becomes quasi-periodic and does not pass the same point after one revolution (see Fig. 1b). This idea has been used as an indicator for process stability for time domain simulation models of milling process in Refs. [8,9,10] as well as for milling experiments in Refs. [11,12,13]. In reality, the actual TCP position is not known. Hence, for the milling experiments, acceleration signals from a sensor placed at the main spindle were used for the analysis. Despite this approximation, promising results were achieved in Refs. [12, 13].
In this paper, we propose the use of a main spindle-mounted tri-axial acceleration sensor for the creation of Poincaré maps and hence for process stability monitoring. Acceleration signal packages of 0.3 s are analyzed for chatter vibrations. This is a moving window where the calculations regarding process stability are performed every 0.1 s. The latest 0.1 s signal is added to the analysis window, and the oldest 0.1 s is removed from the window. In this way, the maximum delay for detecting chatter is 0.1 s.
The accuracy and reliability of chatter detection is heavily dependent on the quality and sharpness of the spindle displacement trajectory. Therefore, extensive signal processing of the raw acceleration signal is performed to obtain a sharp, noise-free trajectory on the Poincaré map. This is achieved by time integration of the raw acceleration signal, removing of trends, periodic regression, and applying a high pass filter. These processing steps were established through initial trials and are performed in real time every 0.1 s.
Besides the acceleration, the angular position of the tool is also recorded from the control system. This is necessary for creation of the Poincaré section. Each deflection of the spindle in the two-dimensional plane is allocated the corresponding angular position. A particular angular position on the Poincaré map can then be observed every revolution. This point is called the bisection point. For a stable process, the trajectory passes nearly the same point at a given angle, and the bisection points lie close to each other, whereas in case of instability, the trajectory is quasi-periodic and bisection points are scattered (see Fig. 1b). Using the trajectory and the bisection points, the criteria for detecting process stability and instability can be established.
The proposed method with a spindle-mounted acceleration sensor is effective only for modes for which the sensor does not lie on one of the nodes of vibration. In case of long and flexible milling tools, the chatter vibrations may not be observable at the spindle-mounted sensor. Hence, observability of chatter vibrations is a necessity for this approach.
2.1 Chatter indicator and criteria for detecting instability
For detecting the transition from stability to instability, the ratio of the standard deviations of the bisection points, \(s_{{{\text{B}}x}}\) and \(s_{{{\text{B}}y}}\), to that of the complete trajectory, \(s_{{{\text{T}}x}}\) and \(s_{{{\text{T}}y}}\), is used as the chatter indicator (CI) (\(CI_{\text{in}}\)), and is calculated accordingly every 0.1 s [13, 14]
For a stable process, this ratio remains small (below 0.1) and increases owing to instability (above 0.8). The course of the CI during the cut can be used as an indication of the transition from stability to instability, and the various criteria used for the detection are illustrated in Fig. 2.
Four criteria are proposed in this paper for the recognition of instability: positive trend, positive leap, absolute limit, and gradient analysis. These criteria are based on the current and previous values of CI. A sudden increase in the amplitude of the CI can be identified as instability using the positive leap criteria, where the amplitude of the current CI is compared with the mean of the previous five CIs. Here, a limiting leap factor Lp must be defined. A gradual increase in the course of CI can be identified as chatter by the positive trend criteria. A boundary trend factor Tp defines the factor by which the present \(CI_{\text{in}}\) exceeds the previous CI. If this occurs for the current and the previous three CIs, a critical trend indicating chatter is detected. In several cases, it was observed that, owing to some unfiltered noise in the acceleration signal, the chatter indicator could not exceed the previous CI by a factor Tp, but an increasing trend was still observed (see Fig. 2d). To cover such cases, a gradient analysis criterion was created where the gradient between the current CI and the fifth last CI was calculated and a limit G was set. Additionally, as a safety measure, an absolute value of Ap was set.
2.2 Chatter indicator and criteria for detecting stability
The proposed method for rapid measurement of SLDs involves not only continuously increasing depth of cut, but also the variation in spindle speed. In case of the latter, the process may pass through one or more stability lobes. Therefore, the detection of the transition from instability to stability is also relevant. For this, the criteria for detecting instability were modified such that negative leaps Ln, trends Tn, and absolute limits An could be detected (see Fig. 2).
It was observed that the application of the stability detection criteria to the CI described in Eq. (1) led to inconsistent and erroneous results. During chatter, the spindle trajectory and bisection points are distributed quasi-periodically and non-deterministically, the CI fluctuates significantly and a transition to stability is difficult to establish. An alternative chatter indicator is proposed here which relates the current Ic to the CI during stable cutting conditions Is:
In other words, it is the ratio of the current chatter indicator to that during stability. In this manner, a reference to the process condition during stability is maintained, and the detection of the transition to stability is easier. As soon as chatter is detected using the Iin from Eq. (1), the CI for the time package preceding the current CI is chosen as the indicator during stability CIs, and the indicator is switched to Ist from Eq. (2) until stability is detected. The complete chatter and stability detection algorithm is implemented as a software in a Matlab environment.
3 Experimental setup
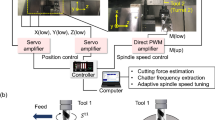
The milling experiments were conducted on a 5-axis machining center carrying a four-toothed milling cutter head of diameter 50 mm with coated carbide cutting inserts (R390-18 06 08 M-PM 4230). C45 steel work pieces with dimensions of 217 mm × 217 mm, fixed with four M12 screws, provided a basis for the different milling operations, as shown in Fig. 3. A tri-axial acceleration sensor was mounted on the spindle housing. An external interpolator was used to extract the current angular position of the spindle from the machine control.
Firstly, an SLD within the range 1 200–1 500 r/min was obtained conventionally. The measurement points with different combinations of depth of cut and spindle speed lead to the stability lobe that is shown in Fig. 3b.
For the rapid determination of stability boundaries, two cuts with different cutting parameters were performed successively. In the first cut, the depth of cut, starting at 2.5 mm with a constant spindle speed of 1 300 r/min, was continuously raised until chatter was detected. This was possible owing to the inclination of the workpiece created by rotating the B-axis (see Fig. 3). After a pause of 5 s, where the chatter detection software reinitializes, the second cut was initiated by increasing the spindle speed and keeping the depth of cut constant. Here, the spindle speed was varied starting from 1 300 r/min till the edge of the workpiece for different rates of spindle speed variation. Furthermore, as communication is required between the chatter detection software and the NC program, the digital input/output interface X142 of the Siemens numerical control unit (NCU) was utilized. Synchronous commands continuously monitored the digital signal from the chatter detection algorithm and switched to a spindle speed variation subroutine as soon as it received the signal.
4 Results and discussions
Five experiments were conducted with the same parameters as mentioned in the previous chapter to roughly analyze the repeatability and consistency of the detected stability and instability boundaries. An example analysis of trial 3 is described in this section (see Fig. 4).
Figure 4 shows the two consecutive milling cuts with the corresponding acceleration signals and calculated chatter indicators. In the case of Cut 1, where the depth of cut is increased continuously on account of the inclined workpiece, Iin is used as an indicator for detecting instability. As can be seen in Fig. 4a, the onset of chatter seen in the acceleration signal is accompanied by a clear increase in Iin. This increase is recognized as instable by the gradient analysis criteria. A digital signal is then sent to the machine control system. The software also calculates the critical depth of cut based on the feed rate and the time of chatter (see Table 1). Owing to the inclined workpiece, the tool experiences minimum and maximum depths of cut (see Fig. 5). The average of the two is taken as the effective depth of cut and is listed in Table 1 as the calculated critical depth of cut \(a_{\text{p, calculated}}\).
It is observed that there is a constant delay of 0.3 s until the feed and spindle are stopped after recognition of chatter. This means that the process is stopped at a higher depth of cut of an additional 0.16 mm for the used feed rate, workpiece inclination, and spindle speed. The process stops at a point around 0.16 mm above the detected stability boundary.
After a pause of 5 s, the spindle speed variation is automatically initiated at the same depth of cut. For this cut, the indicator Ist from Eq. (2) is calculated online, and the criteria for negative leap, trend, and absolute limit are applied. Stability is detected at 1 465 r/min by the negative trend criteria, but the spindle speed is varied till the end of the workpiece. After this point, the chatter indicator is switched back to Iin, as the transition to instability will now be searched.
The five milling trials were carried out for the same workpiece inclination angle, but for different spindle accelerations (\({\text{r}}/\left( {\hbox{min} \cdot {\text{s}}} \right)\)), as can be seen in the Table 1. As far as Cut 1 is concerned, a very high agreement can be seen between the calculated and measured critical depths of cut. In general, however, the critical depth of cut for an inclined workpiece seems to be marginally higher than in the case of a conventional slot. For Cut 2, the spindle speed was varied at different rates of change in spindle speed, which is referred to as “spindle acceleration” (\({\text{r}}/\left( {\hbox{min} \cdot {\text{s}}} \right)\)) [6].
For different rates of change in spindle speed, different boundaries were obtained. The conventionally obtained SLD shows that for a cutting depth between 7 mm and 7.5 mm, the stability boundary lies roughly between 1 325 r/min and 1 375 r/min. However, the detected boundaries, taken from the average of the maximum and minimum depths of cut (see Fig. 5) lie slightly lower than the conventionally obtained boundaries (see Table 1 and Fig. 6). Higher spindle revolutions per minute accelerations show a higher deviation from the actual stability boundary. A reasonably accurate stable spindle speed was detected only for the low rate of spindle speed variation of 23.1 \({\text{r}}/\left( {\hbox{min} \cdot {\text{s}}} \right)\). Due to the dimensions of the workpiece, a subsequent Cut 3 with increases in depth of cut was not possible.
5 Conclusions
This study proposes a combination of experimental techniques of continuously increasing the depth of cut and continuously varying spindle speed such that SLD can be obtained rapidly and automatically. For this, a real-time chatter detection algorithm based on the Poincaré section was developed and implemented for detection of instability as well as stability. All mathematical operations regarding calculation of CIs and the criteria can be performed in real time, and stability and instability were detected with a maximum delay in recognition of 0.1 s. A communication with the machining center was established via the digital input/outputs of the NCU.
Promising preliminary results were obtained for the combination of the experimental techniques. The critical depth of cut for a given spindle speed could be identified accurately and quickly. The boundary of stability at a given depth of cut could be identified with reasonable accuracy only in the case of a low rate of change in spindle speeds. This appears to be a limitation of the proposed method as a larger workpiece is required for low revolution per minute accelerations. For larger workpieces, the position dependent machine dynamics may lead to a distortion or falsification of the SLD. Further experimentation is required to analyze the effect of rate of change in spindle speed to find an optimum value for a given process.
References
Tlusty J, Ismail F (1981) Basic non-linearity in machining chatter. Ann CIRP 30:299–304
Altintas Y, Budak E (1995) Analytical prediction of stability lobes in milling. Ann CIRP 44:357–362
Altintas Y, Budak E (1998) Analytical prediction of chatter stability in milling—part I: general formulation. J Dyn Syst Meas Control 120(1):22–30
Altintas Y, Budak E (1998) Analytical prediction of chatter stability in milling—part II: application of the general formulation to common milling systems. J Dyn Syst Meas Control 120(1):31–36
Quintana G, Ciurana J, Teixidor D (2008) A new experimental methodology for identification of stability lobes diagram in milling operations. Mach Tools Manuf 48:1637–1645
Grossi N, Scippa A, Sallese L et al (2015) Spindle speed ramp-up test: a novel experimental approach for chatter stability detection. Mach Tools Manuf 89:221–230
Davies MA, Dutterer B, Pratt JR et al (1998) On the dynamics of high-speed milling with long, slender endmills. Ann CIRP 47:55–60
Surmann T (2005) Geometric-physical simulation of the process dynamics for five-axis milling of free-form surface. Dissertation, Dortmund University
Honeycutt A, Schmitz T (2016) A new metric for automated stability identification in time domain milling simulation. J Manuf Sci Eng 138(7):074501
Schmitz T, Medicus K, Dutterer B (2002) Exploring once-per-revolution audio signal variance as a chatter indicator. Mach Sci Technol 6(2):215–233
Brecher C, Epple A, Fey M (2014) Efficient determination of optimal process parameter. wtWerkstatttechnik online 104:260–265
Brecher C, Kiesewetter C, Epple A et al (2015) Automated creation of stability lobes diagrams for milling. ZWF 110(4):191–195
Brecher C, Chavan P, Epple A (2017) Efficient determination of stability boundaries. wtWerkstattstechnik online 107(5):313–317
Brecher C, Daniels M, Wellmann F et al (2015) Realisation of efficient cutting processes. Result report of the BMBF—joint project ReffiZ. Shaker-Verlag, Aachen
Acknowledgements
The authors wish to gratefully acknowledge the support of the German Research Foundation (Deutsche Forschungsgemeinschaft, DFG). This work was funded as part of the DFG Project “Efficient determination of Stability Lobe Diagrams” (Grant No. BR 2905/73-1).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Brecher, C., Chavan, P. & Epple, A. Efficient determination of stability lobe diagrams by in-process varying of spindle speed and cutting depth. Adv. Manuf. 6, 272–279 (2018). https://doi.org/10.1007/s40436-018-0225-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40436-018-0225-x