1 Introduction

Rotating machinery is an essential asset in many industries such as aviation, power generation, oil, and mining. Increasing the efficiency of rotating machines usually requires higher operating speeds, lighter components, and reduced clearance between moving and stationary parts. However, these requirements may yield the rotating equipment to be prone to various defects such as bent shafts, shaft cracks, and rotor–stator rubbing. Rotor–stator rub is one of the serious malfunctions that may occur in rotating machines as a result of tight clearances between rotating and stationary components along with high vibration amplitudes caused by excessive eccentricity, changes in mass imbalance, passage through critical speeds, or other vibration sources. The resulting vibration response due to rubbing is very complicated and may lead to machine failure. Hence, accurate prediction of the rubbing response is essential to avoid machine damage and maintain safe and reliable operation of rotating machinery. A large and growing body of literature has been published on the rotor–stator rubbing phenomenon. Detailed literature reviews on rotor–stator rubbing are given by [1,2,3,4] to describe the observed phenomena, identify the rub-related vibration characteristics, and summarize the theoretical and experimental research contributions. Recently, Prabith and Krishna [5] presented a comprehensive review of the numerical modelling of rotor–stator rubs showing several kinds of rub and the characteristics of rub responses.

The influence of rotor–stator rubbing interactions on the response of rotor systems has been widely investigated. When a rotating part comes in contact with a stationary part, the rotor experiences impacts, friction, and stiffening [1]. The switching between the contact and non-contact states during rubbing causes a strong nonlinearity in the dynamic response [2]. Consequently, significant changes are observed in the resulting dynamic response of the rotor. Earlier studies focused on developing mathematical models to simulate the rubbing phenomenon and to identify the distinguishing characteristics of rubbing in the frequency spectrum [6,7,8,9]. The presence of subharmonic frequency components in the frequency spectrum was observed and explained by various researchers [10, 11]. Ehrich [12] showed the presence of strong subharmonics as low as (1/32 ×) and super harmonics as high as 9 × in the frequency spectrum of rubbing.

Generally, rubbing has two main forms, partial rubbing and full annular rubbing [13]. In partial rubs, the rotor contacts the stator intermittently at some portions [14,15,16]. Abuzaid et al. [17] showed experimentally and analytically that the vibration waveform becomes flattened in some portions and the fundamental frequency component is attenuated due to the resulting friction from partial rubbing. Ma et al. [18] analyzed the vibration characteristics of a two-disk rotor system with fixed point rubbing and local-arc rubbing conditions. Silva et al. [19] used the continuous wavelet transform (CWT) to analyze vibration acceleration signals of gas turbines for early detection of a single-point rub of a rotor with a flexible casing. Another form of rubbing is the full annular rub motion in which the rotor maintains continuous contact with the inner surface of the stator. Full annular rubbing represents a nonlinear rotor response under the effect of several combined excitation forces; centrifugal unbalance force, contact forces, and elastic force [20]. The whirling vibration due to full annular rubbing can be synchronous, i.e., forward whirl whose frequency equals to the rotor’s spinning frequency. Dai et al. [21] analyzed both the numerical and experimental vibration response of a rotor rubbing with a motion-limiting stop and explained that full rubbing occurred when the amplitude of the excitation force increased past a certain value. Full annular rubbing may also exhibit the self-excited dry friction backward whirl which is the most destructive rubbing scenario. In this severe condition, the rotor whirls in a backward direction to the rotor’s spinning speed with a super-synchronous frequency and experiences very high amplitudes [22, 23]. Choi [13] explained the onset and vanishing of the backward whirl using experimental and numerical approaches. Shang et al. [24] derived the different solutions of the nonlinear rotor–stator rub system taking the dry friction into account to identify the global response characteristics and draw boundaries of the different responses in the same parameter space. Chen et al. [25] studied analytically the forward and backward full annular rubs in a rotor-casing/foundation system.

Owing to the strong nonlinearity associated with the rubbing phenomenon, the dynamic response is very sensitive to initial conditions and changing system parameters [26,27,28,29,30,31,32]. Nonlinear systems are characterized by the coexistence of attractors. Hence, jump phenomena can occur from one attractor to another due to small perturbations, such as changing the running speed, excitation forces, or perturbation conditions. The rotor–stator rubbing system usually encounters this condition [33]. Consequently, a rich profile of periodic, quasi-periodic, and chaotic responses has been observed for rotor–stator rubbing systems in previous literature [34,35,36,37,38]. This was illustrated through orbit plots, Poincare maps, and bifurcation diagrams. Coexisting and alternating periodic and chaotic responses have been reported by many researchers as in Refs. [13, 24, 36]. Chaotic response is characterized by non-repetitive, irregular orbits and dispersed patterns of points in Poincare maps [5]. Several routes to chaos have been observed in rotor–stator rubbing, namely, period-doubling, quasi-periodic, intermittency, and sudden transitions [26, 28]. Bently et al. [39, 40] showed experimentally the effect of the support stiffness on the onset of backward full annular rub. It was indicated that backward full annular rub is likely to occur when the foundation is stiff, while forward annular rub would appear on a flexible foundation. In [13], the role of the coefficient of friction was emphasized in explaining the onset of a backward whirl. Also, the results indicated that the rotor eccentricity is a key parameter in determining the final operating speed of the backward slipping. Zhang et al. [20] studied analytically and numerically the synchronous full annular rub motion (SFARM) of a rotor for the two cases of rigid and flexible stator conditions. The results showed that the running speed, the damping of the rotor, and the coefficient of friction can significantly affect the vibration response nature and stability in the case of the rigid stator. However, for the flexible stator, the important parameters are the running speed, the ratio of the stator stiffness to the rotor stiffness, the damping ratios for both rotor and stator, and the coefficient of friction.

The nonlinear dynamic behavior of rotor–stator rub-interactions has been investigated using several approaches. Mostly, numerical studies are established using lumped parameter models with low degrees of freedom to maintain reasonable computation time as in Refs. [29, 31, 34, 37, 41,42,43]. The contact between rotor and stator is mostly modeled using the piecewise linear force model and the classical Coulomb’s friction model such as [8, 41, 44, 45]. However, some studies have utilized other contact models such as the viscoelastic Kelvin–Voigt model [27, 46] and the piecewise nonlinear force model [47,48,49]. In an interesting recent study, Li et al. [50] studied the effect of viscous friction instead of dry Coulomb friction and found that viscous friction has a significant effect on the region of forward full annular rubbing. However, its effect on the region of backward full annular rubbing is not important. Other approaches for studying the rotor–stator rubbing responses include finite element modeling (FEM) such as [18, 19, 48, 51], and analytical solutions as in [17, 20, 25, 52, 53]. Experimental studies have been conducted to verify theoretical results by simulating rotor–stator rubbing on laboratory rigs. Chu and Lu [54] built an experimental rig with a special stator structure that can be used to simulate full annular rub, and rubbing experiments were performed on it with different conditions. Results demonstrated that periodic responses with 1/2 × subharmonic appeared with multiple harmonic components 2 × , 3 × , etc. In some special cases, the 1/3 × subharmonic series also appeared with multiple harmonics, and the quasiperiodic response was found for special conditions. Moreover, a chaotic response occurred when the rubbing became severe. However, it was difficult to trace the routes to and out of chaos because of the speed fluctuations. Ma et al. [55] carried out experiments to verify the finite element model of a fixed-point rubbing system. Both numerical and experimental results showed that the system experienced a transition from period-1, through period-2, to period-3 motions. They suggested that the 2 × harmonic, 1/2 × , and 1/3 × subharmonics and the normal rubbing forces are diagnostic indicators of rubbing severity. Mokhtar et al. [56] performed an experimental research on the torsional vibration due to rotor–stator rubbing. Most recently, Yu et al. [57] used dual complexity parameters and variational mode decomposition to identify the rub impact fault from measured vibration signals on an aircraft engine rotor tester.

In this paper, experimental work is carried out on a laboratory rig to simulate rotor–stator rub and analyze the nonlinear rub response. Moreover, a two degrees of freedom nonlinear model is presented to study the lateral vibrations of the rotor and perform further parametric analysis. The influence of radial clearance and mass unbalance on the response of the rotor is experimentally and numerically investigated. Also, the effect of varying initial conditions on the rotor rub response is studied.

The paper is outlined as follows: in Sect. 2, the details of the laboratory test rig and the experimental procedure are presented. In Sect. 3, the experimental results are discussed. In Sect. 4, the mathematical model of a Jeffcott rotor is introduced. In Sect. 5, the numerical results are given using the same parameters as the experimental rig.

2 Experimental setup

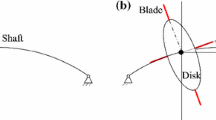
Figure 1a shows the experimental setup used to investigate lateral vibrations of a Jeffcott rotor model. The G.U.N.T® machinery fault demonstrator (PT500) consists of a variable-speed electric motor (0.37 kW) that drives a uniform steel shaft through a flexible coupling. The rotating shaft is supported by two rolling element bearings (SKF 6004-2ZR) at its both ends. A rigid disk is fastened at the midspan of the shaft by a taper lock.

Fig. 1
figure 1

a A photo of the PT500 G.U.N.T® laboratory rig; b a schematic diagram indicating details of the stator device

Full size image

A special stator device is designed and manufactured as shown in Fig. 1b. The stator support is made of steel with high stiffness and is bolted to the base of the test rig. The stator has a central hole in which a tapered ring with a taper ratio of 3:14 is fitted. To protect the rotor from abrasion during the experiments, the inner ring of the stator is made of soft copper alloy. The diameter of the copper ring is slightly larger than the disk’s diameter. The stator device can be moved along the shaft from left to right so the radial clearance between the disk and the stator can be adjusted in the range of 0–5 mm and measured using feeler gauges.

The lateral vibration signals are picked up by the two proximity transducers (FK-452F) located near the disk (see Fig. 1a). The experimental findings are acquired at a sampling frequency of 4000 Hz, and the number of samples is taken as 16,000 samples with a time span of 4 s. Table 1 presents the physical and geometrical details of the laboratory machine.

Table 1 Geometric parameters of PT500 G.U.N.T® laboratory machine
Full size table

3 Experimental results and discussion

In this section, two experiments are conducted to discuss the whirling response with rub fault in the rotor–stator experimental system. First, the effect of changing mass unbalance on the whirling motion is studied to simulate the effect of increasing centrifugal forces on rotor–stator rubbing onset in practical machinery. Excessive lateral vibration due to several practical reasons may cause a reduction in the radial clearance (gap) between the rotor and the stator. Hence, the second experiment illustrates the effect of changing radial clearance on the whirling motion. LabVIEW® software is used to analyze the measured signals. Time waveforms, frequency spectra, orbit plots, and Poincaré’s maps are utilized to observe and analyze the experimental signals.

3.1 Case I: studying the effect of the mass unbalance

The radial clearance \(\delta \) is adjusted to 0.15 mm, and the rotor is run at 3226 rpm. It is found by experiment that the range of speeds where the onset of contact is observed on the test rig is above 2000 rpm. Hence, the rotational speeds are selected above this value. Figure 2 shows the dynamic response of the rotor system with mass unbalance \({m}_{u}\)= 6.588 g. Hence, the resulting orbit plot (Fig. 2i) is almost circular and Poincaré’s points (Fig. 2ii) are clumped together which indicates a period-1 response. Moreover, the spectra show 1 × , 2 × , and 3 × frequency components (Fig. 2iv). When the mass unbalance is increased to 13.2 g with the same radial clearance (0.15 mm) and at the same speed (3226 rpm), the system experiences serious impact, and a heavy chaotic response takes place as shown in Fig. 3. The spectra in Fig. 3iv show a significant change as more harmonics appear up to 5 × component.

Fig. 2
figure 2

Experimental results for the rotor system at speed = 3226 rpm, \({\varvec{\delta}}\)= 0.15 mm, and \({{\varvec{m}}}_{{\varvec{u}}}\) = 6.588 g, i orbit plot; ii Poincaré’s map; iii time waveforms; and iv frequency spectra

Full size image
Fig. 3
figure 3

Experimental result for the rotor system at speed = 3226 rpm, \({\varvec{\delta}}\)= 0.15 mm, and \({{\varvec{m}}}_{{\varvec{u}}}\) = 13.2 g, i orbit plot; ii Poincaré’s map; iii time waveforms; and iv frequency spectra

Full size image

By comparing Figs. 2iv and 3iv, attenuation of the horizontal 1 × amplitude is observed from 0.01695 to 0.01173 mm, which could be attributed to the rotor’s stiffening effect due to heavy rubbing [1, 17]. However, the vertical 1 × amplitude experiences an increase from 0.01398 to 0.01829 mm. This observation, together with the different vibration pattern in both horizontal and vertical time waveforms and corresponding spectra, suggests the presence of misalignment or a slight eccentricity between the rotor and stator geometric centers. Further inspection of Fig. 3 shows low-amplitude 1/2 × , 3/2 × , and 5/2 × components in Fig. 3iv, which may indicate coexisting chaos with period-2 motion.

3.2 Case II: studying the effect of the radial clearance

The following findings present the effect of changing the radial clearance on the rub fault responses. The stator device is moved along the shaft axis to adjust the radial clearance between the disk and the stator’s inner ring. The influence of changing this parameter is significant in the orbit plot, Poincaré’s map, and especially in the spectra, as seen in Figs. 4, 5, and 6 for the following radial clearance values: \(\delta \)= 0.25 mm, \(\delta \)= 0.15 mm, and \(\delta \)= 0.1 mm respectively. These values were measured using feeler gauges. The following results are measured at \({m}_{u}\)= 6.588 g and 3542 rpm. When the radial clearance is 0.25 mm, the orbit plot and Poincaré’s map (Fig. 4i, ii) depict light impact. Moreover, the spectra show high amplitudes at the super-harmonic components (2 × and 3 ×) in the vertical direction (see Fig. 4iv) and a low-amplitude 1/2 × component. From the frequency spectra (Fig. 4iv) and the truncated waveforms (Fig. 4iii), it can be inferred that the resulting signal experiences a chaotic response with coexisting period-2 motion.

Fig. 4
figure 4

Experimental results for the rotor system at speed = 3542 rpm, \({{\varvec{m}}}_{{\varvec{u}}}\)= 6.588 g, and \({\varvec{\delta}}\)= 0.25 mm, i orbit plot; ii Poincaré’s map; iii time waveforms; and iv frequency spectra

Full size image
Fig. 5
figure 5

Experimental results for the rotor system at speed = 3542 rpm, \({{\varvec{m}}}_{{\varvec{u}}}\)= 6.588 g, and \({\varvec{\delta}}\)= 0.15 mm, i orbit plot; ii Poincaré’s map; iii time waveform; and iv frequency spectra

Full size image
Fig. 6
figure 6

Experimental results for the rotor system at speed = 3542 rpm, \({{\varvec{m}}}_{{\varvec{u}}}\)= 6.588 g, and \({\varvec{\delta}}\)= 0.1 mm, i orbit plot; ii Poincaré’s map; iii time waveform; and iv frequency spectra

Full size image

Figure 5 gives the dynamic response of the rotor system at 0.15 mm for radial clearance. The trajectories of the resulting signal show chaotic motion. The spectra demonstrate the same harmonic components as the previous one but with increased amplitude (Fig. 5iv). Likewise, Poincaré’s map (Fig. 5ii) has more forked points than the previous case. Figures 5iv and 2iv represent the rotor response with the same mass unbalance and at the same clearance, but the rotational speed is the only different parameter. Hence, comparing the two figures shows that the increase in the running speed gives rise to an increase in the amplitudes of the 1 × , 2 × and 3 × components. However, the increase of the 2 × , and 3 × harmonics is more pronounced.

When the radial clearance is reduced to 0.1 mm (Fig. 6), it is clear that the rubbing between the rotor and the stator is becoming more severe as the gap between the rotor and stator is getting smaller. The frequency spectra contain the same harmonics (1 × , 2 × , and 3 ×), but their amplitudes show an increase (Fig. 6iv). For instance, the horizontal 1 × amplitude was equal to 0.01172 mm for \(\delta \) = 0.25 mm and increased to 0.01763 mm for \(\delta \) = 0.15 mm. Then, for the third case of \(\delta \) = 0.1 mm, the horizontal 1 × amplitude is 0.02193 mm. The orbit plot, Poincaré’s map, and truncated waveforms confirm the response condition as chaotic with coexisting period-2 motion, as seen in (Fig. 6i, ii, iii). It is apparent from these findings that impacts between the rotor and the stator are very sensitive to the change in the radial clearance. This is reflected in the increase in the amplitude of the harmonic components in both directions. However, the increase of the 2 × and 3 × harmonic components in the vertical direction is easily discernible. Moreover, their increase occurs for the increasing of the mass imbalance and the running speed, and for decreasing the radial clearance as well. Hence, it can be inferred that these components are very sensitive to rubbing aggravation.

4 Theoretical analysis

In this section, a lumped parameter two-degrees-of-freedom model of the experimental rotor–stator system is established. Then, the governing equations of the lateral vibration of the rotor system are formulated. Moreover, the assumptions of the mathematical contact model are presented.

4.1 Rotor–stator model

A Jeffcott rotor model is used to describe the experimental rotor–stator system used in this research. Figure 7a shows the rotor–stator system that is simulated by one disk which represents the total mass of the rotor system, and an elastic shaft with restricted ends. The disk is assumed to be at the midspan of the shaft. Figure 7b represents the whirl of the rotor due to the existence of lateral vibration. As shown in Fig. 7b, mass unbalance is denoted as \({m}_{u}\) and the rotor rotates around the eccentric center \({c}_{p}\) with eccentricity distance e. The rotor rotates with a constant speed \(\omega \) in counterclockwise direction (CCW) and may exhibit impacts with the stator during rotation.

Fig. 7
figure 7

A schematic demonstrating a the lumped mass model of the rotor–stator system; and b the configuration of the contact between the disk and stator

Full size image

The equations of motion of a rotor–stator system is established by using a coordinate system (x–y–z), (as shown in Fig. 7a). The radial clearance between the disk and the stator is denoted by \(\delta \). The radial displacement of the rotor is r = \(\sqrt{{x}^{2}+{y}^{2}}\), hence the equations of motion can be written as:

$$ \begin{array}{*{20}c} {m\ddot{x} + C_{b} \dot{x} + K_{b} x = F_{{\text{x}}} + m_{u} e\omega ^{2} \cos \left( {\omega t} \right)} \\ {m\ddot{y}+ C_{b} \dot{y} + K_{b} y = F_{{\text{y}}} + m_{u} e\omega ^{2} \sin \left( {\omega t} \right) - mg} \\ \end{array} $$
(1)

The physical parameters of the system are m, \({C}_{b}\), and \({K}_{b}\), which represent the mass, damping coefficient, and stiffness of the rotor system, respectively. \({F}_{x}\) and \({F}_{y}\) are the nonlinear forces that are generated from the impact between the rotor and stator. Table 1 provides the values of system parameters.

4.2 Contact model

The impact between the rotor and stator is described by a viscoelastic contact model. Contact may lead to plastic deformation in one of the contact surfaces (see Fig. 7b) and induce the system nonlinearity [5]. According to the Coulomb friction law, a normal force, and a tangential force, i.e., perpendicular to the normal force, as seen in Eqs. (2) and (3) are expressed as follows:

$${F}_{{\text{n}}}=\lambda *\left({K}_{{\text{s}}}*\gamma +{C}_{{\text{s}}}*{V}_{{\text{n}}}\right)$$
(2)
$${F}_{{\text{t}}}={F}_{{\text{n}}}*\mu * \left[{\text{tanh}}\left(\frac{{V}_{{\text{r}}}}{{X}_{{\text{s}}}}\right)+\frac{\frac{{V}_{{\text{r}}}}{{X}_{{\text{s}}}}}{1+{\left(\frac{{V}_{{\text{r}}}}{{X}_{{\text{s}}}}\right)}^{2}}\right]$$
(3)

where \({K}_{{\text{s}}}\) and \({C}_{{\text{s}}}\) are the contact stiffness and contact damping coefficient of the stator device, respectively. The penetration of the rotor into the stator is given as (\(\gamma \) = \(r-\delta )\), and the friction coefficient is µ. To enhance the stability of the numerical analysis, the variation of the friction coefficient µ with the relative velocity \({V}_{{\text{r}}}\) is smoothed using the continuous function shown in Eq. (3). The steepness parameter \({X}_{{\text{s}}}\) is used to define the static friction behavior range. As \({X}_{{\text{s}}}\) approaches unity, the precision of the approximation is enhanced. In this study, it is found that \({X}_{{\text{s}}}\) = 0.5 is sufficient for stable numerical simulation for the given parameters. A switching function \(\lambda \) determines whether the contact has occurred or not as shown in Eq. (4), i.e., contact condition or non-contact condition.

$$\lambda = \left\{\begin{array}{cc}1& \gamma >0\\ 0& \gamma \le 0\end{array}\right\}.$$
(4)

The normal velocity of the rotor \({V}_{{\text{n}}}\) is determined from Eq. (5), while \({V}_{{\text{r}}}\) is the relative contact velocity which is given by Eq. (6). The whirling angle of the rotor axis is denoted by \(\alpha \), where cos \(\alpha \) = \(\frac{x}{r}\) and sin \(\alpha \) = \(\frac{y}{r}\). The outer diameter of the disk is described by \({D}_{{\text{o}}}\). The parameters of the contact model are listed in Table 2.

Table 2 Parameters of the contact model
Full size table
$${V}_{{\text{n}}}= \dot{x}{\text{cos}}\alpha + \dot{y}\mathrm{ sin}\alpha $$
(5)
$${V}_{{\text{r}}}= -\dot{x}\mathrm{ sin}\alpha + \dot{y}{\text{cos}}\alpha + \frac{{D}_{{\text{o}}}}{2}*\omega .$$
(6)

After the normal force and tangential force are calculated, they are projected to the x-axis and y-axis to evaluate the nonlinear forces in both directions by using the superposition technique, so that:

$${F}_{{\text{x}}}={-F}_{{\text{n}}}*{\text{cos}}\alpha +{F}_{{\text{t}}}*{\text{sin}}\alpha .$$
(7)
$${F}_{{\text{y}}}={-F}_{{\text{n}}}*{\text{sin}}\alpha -{F}_{{\text{t}}}*{\text{cos}}\alpha .$$
(8)

5 Numerical results and discussion

In this section, the whirling motion response of the rotating system with the effect of mass unbalance and radial clearance parameters is discussed through two cases studies. The equations of motion given by Eq. (1) are solved using MATLAB®’s ode45 (hybrid fourth/fifth order Runge–Kutta) technique. The used relative tolerance was \({10}^{-5}\), and the absolute tolerance was \({10}^{-12}\). The time step was set to \({10}^{-5}\) and the initial conditions are assigned as the static deflection of the rotor system with zero initial velocity unless otherwise stated.

In addition, bifurcation analysis is carried out to precisely analyze the dynamics of the rotor system over a certain range of rotating speeds that are limited to 4200 rpm to match the speed limit of the experimental rig. In particular, zones with unique features are analyzed through the orbit plot, Poincaré’s points, FFT spectra, and time waveforms. The orange circle and orange line in the orbit plot and waveform, respectively, represent the radial clearance limit.

5.1 Case study 1: mass unbalance variation with constant radial clearance

Here, the obtained results demonstrate the effect of changing the mass unbalance on the whirling vibration of the rotating system. Figure 8 represents the bifurcation analysis that monitors the radial displacement of the rotor with changing the rotational speed where the mass unbalance is set to 6.588 g and \(\updelta \) = 0.15 mm. The control parameter is set as the running speed because, in real industrial applications such as power plant units, rubbing is likely to occur when the speed is increased or when the rotor passes through a critical speed. Bifurcation analysis shows the periodic response of the rotor system without contact from 2500 to 3770 rpm approximately. Then, significant changes are observed in the range from 3770 to 4200 rpm. The onset of rubbing starts with period-1 with coexisting slight chaos at 3775 rpm (see Fig. 8b). This finding is very close to the experimental results represented earlier; however, the speeds are not exactly equal. Experimentally, the onset of rubbing appears earlier than that for the theoretical result. This can be considered acceptable as the theoretical model is idealized when compared with the experimental setup. However, both numerical and experimental findings agree in the presence of coexisting periodic and chaotic responses after rubbing onset.

Fig. 8
figure 8

a Numerical bifurcation analysis of the radial displacement showing the effect of mass unbalance \({{\varvec{m}}}_{{\varvec{u}}}\)= 6.588 g, at \({\varvec{\delta}}\)= 0.15 mm; and b zoomed-in view

Full size image

After that, the mass unbalance is increased to 13.2 g (see Fig. 9). The bifurcation analysis demonstrates that there is a periodic response with no contact from 2500 to 3360 rpm. Meanwhile, the onset of the contact occurs at 3365 rpm, at which the lateral motion is period-1 and is followed by high intensity chaotic response directly after that speed (see Fig. 9). It is noted that the amplitude of rotor–stator rub response at low mass unbalance (Fig. 8) is lower than that at high mass unbalance (Fig. 9). In addition, at high unbalance mass, the rub starts earlier than that at low unbalance mass. This behavior points out that when the centrifugal force due to unbalance is increased, a complex rub response is exhibited as obtained via experimental results.

Fig. 9
figure 9

a Numerical bifurcation analysis of the radial displacement showing the effect of mass unbalance \({{\varvec{m}}}_{{\varvec{u}}}\)= 13.2 g, at \({\varvec{\delta}}\)= 0.15 mm; and b zoomed-in view

Full size image

Figure 10 demonstrates the lateral vibration responses at \({m}_{u}\) = 6.588 g and \(\delta \) = 0.15 mm for different rotating speeds in the range of contact identified by the bifurcation analysis. At 3940 rpm, the resulting response is period-3 where Poincaré’s map contains 3 points (see Fig. 10ia). The whirling vibration becomes more serious and shows a chaotic whirl at 4000 rpm (Fig. 10ii). When the rotating speed is increased to 4135 rpm (Fig. 10iii), the whirling response becomes period-2 motion, as shown by Poincaré’s map and the orbit plot.

Fig. 10
figure 10

Lateral vibration responses at \({m}_{u}\)= 6.588 g and \(\delta \)= 0.15 mm i 3940 rpm, ii 4000 rpm, and iii 4135 rpm a orbit plot and Poincaré’s points; b time waveform; and c frequency spectrum. The orange line represents the clearance limit

Full size image

Figure 11 indicates different lateral vibration responses at \({m}_{u}\) = 13.2 g and \(\delta \) = 0.15 mm. At 3485 rpm, the orbit plot in (Fig. 11ia) illustrates a quasiperiodic response of the rotating system that happened after single-period route. The frequency spectrum (Fig. 11ic) also shows incommensurate frequencies around (1 × , 2 × and 3 ×), and Poincaré’s points form a closed circle of points. A “beat-like” pattern appears in the time waveform (Fig. 11ib). When the rotating speed is slightly increased to 3542 rpm, the behavior changes to a serious chaotic response as shown in Poincaré’s points (see Fig. 11iia).

Fig. 11
figure 11

Lateral vibration responses at \({{\varvec{m}}}_{{\varvec{u}}}\)= 13.2 g and \({\varvec{\delta}}\)= 0.15 mm i 3485 rpm, and ii 3542 rpm a orbit plot and Poincaré’s points; b time waveform; and c frequency spectrum. The orange line represents the clearance limit

Full size image

5.2 Case study 2: radial clearance variation with constant mass unbalance

Herein, additional numerical investigation is conducted to analyze the effect of changing the radial clearance on the whirling response of the rotor system. Bifurcation plot in Fig. 12a exhibits the rotor–stator system response when radial clearance is set to 0.25 mm and \({m}_{u}\)= 6.588 g. Over the specified range of rotating speeds, the bifurcation analysis shows no rub at this radial clearance. Also, studying the dynamics of the rotor–stator system at the radial clearance of 0.15 mm and \({m}_{u}\hspace{0.17em}\)= 6.588 g is performed as shown before in Fig. 8. It is clear that there are random impacts and rub-interactions as indicated in (Fig. 10).

Fig. 12
figure 12

Numerical bifurcation analysis of the radial displacement showing the effect of radial clearance a \({\varvec{\delta}}\)= 0.25 mm; and b \({\varvec{\delta}}\)= 0.1 mm, at \({{\varvec{m}}}_{{\varvec{u}}}\)= 6.588 g

Full size image

Finally, when the radial clearance is decreased to 0.1 mm, a bifurcation analysis (Fig. 12b) indicates that the onset of the contact is at approximately 3695 rpm with period-1 response. The response of the rotating system from 2500 to 3690 rpm is periodic without contact. On the other hand, from 3695 to 3730 the impact is period 1 with contact. After that, when the rotating speed is slightly increased to 3735 rpm, the whirling vibration experiences a sudden transition to chaos as shown in the bifurcation diagram (see Fig. 12b). The observed bifurcation plots highlight a sophisticated dynamic response of the rotor–stator system with complex behavior with radial clearance variation. Moreover, the onset of the impact is very sensitive to the value of the radial clearance, as shown in Figs. 8 and 12b.

Figure 13i indicates the response at 3940 rpm in which a chaotic response is observed with high intensity. When the rotating speed is increased to 4070 rpm, a quasiperiodic response is obtained (see Fig. 13ii). As concluded from the experimental results, decreasing radial clearance has a crucial influence on the dynamic behavior of the rotor–stator system especially the 2 × and 3 × components.

Fig. 13
figure 13

Lateral vibration responses at \({{\varvec{m}}}_{{\varvec{u}}}\)= 6.588 g and \({\varvec{\delta}}\)= 0.1 mm i 3940 rpm; and ii 4070 rpm a orbit plot and Poincaré’s points; b time waveform; and c frequency spectrum. The orange line represents the clearance limit

Full size image

5.3 Case study 3: initial conditions variation

In this section, the observed numerical results illustrate the effect of changing initial conditions on the whirling phenomenon of the rotor system. Figure 14 presents the bifurcation analysis at different initial conditions with mass unbalance 6.588 g and radial clearance 0.1 mm. It is noticed from the bifurcation analysis that the whirling response from 3000 rpm to 3680 is periodic with no contact in the three cases studied. Moreover, the onset of rubbing occurs at 3690 rpm in the three cases, at which the whirling motion is period-1. When the rotating speed is increased from 3700 to 4100 rpm, significant changes occur, and the response characteristics change from period-1 to chaotic response by sudden transition. In addition, bifurcation diagrams present that when the rotating speed increases the intensity of the chaotic response changes from violent to slight. It is noticed from the observed results that at the same rotating speed, the intensity of chaotic response has been affected due to changing the initial conditions (see Fig. 15). Also, quasiperiodic response appears at 4008 rpm for the initial conditions \(({x}_{o}=0.25e-4, {y}_{o}=0.95e-6\)) as shown in Fig. 16b. Qualitatively, the results show the co-existence of different whirling responses such as periodic, quasiperiodic, and chaotic by changing initial conditions for the same operating conditions.

Fig. 14
figure 14

Numerical bifurcation analysis of the radial displacement showing the effect of changing the initial conditions a \({x}_{o}={y}_{o}=0.25e-4\); b \({x}_{o}=0.25e-4, {y}_{o}=0.95e-6\); and c. \({x}_{o}=0.93e-4, {y}_{o}=0.5e-5\)

Full size image
Fig. 15
figure 15

Orbit plot and Poincaré’s points for lateral vibration responses at \({m}_{u}\)= 6.588 g, \(\delta \)= 0.1 mm, and 3755 rpm a \({x}_{o}={y}_{o}=0.25e-4\); b \({x}_{o}=0.25e-4, {y}_{o}=0.95e-6\); and c. \({x}_{o}=0.93e-4, {y}_{o}=0.5e-5\)

Full size image
Fig. 16
figure 16

Orbit plot and Poincaré’s points for lateral vibration responses at \({m}_{u}\)= 6.588 g, \(\delta \)= 0.1 mm, and 4008 rpm a \({x}_{o}={y}_{o}=0.25e-4\); b \({x}_{o}=0.25e-4, {y}_{o}=0.95e-6;\) and c. \({x}_{o}=0.93e-4, {y}_{o}=0.5e-5\)

Full size image

6 Conclusions

In this paper, the rotor–stator rub phenomenon has been investigated experimentally and numerically. The experimental analysis was carried out on the laboratory rig (G.U.N.T® PT500) which simulated the Jeffcott rotor model. A special stator device was manufactured to simulate rubbing between a rotating part and a stationary part. The experimental results showed chaotic response with coexisting periodic response in several case studies. Increasing the value of the mass unbalance was shown to yield more complex chaotic behavior. The 1 × component dominated the spectrum for all the case studies. The 1/2 × subharmonic family appeared with a very low amplitude in the frequency spectra indicating period-2 motion with chaos. Changing the radial clearance has a crucial effect on the rub responses. It was noticed from the frequency spectra that decreasing clearance gave rise to a noticeable increase in the amplitudes of the 1 × , 2 × , and 3 × harmonic components. However, the 2 × and 3 × harmonic components have been found to be very sensitive to increasing the rub severity and can serve as a diagnostic indicator with the aid of orbit plots and time waveforms.

In the numerical study, a two-degree-of-freedom nonlinear model was established, and the lateral vibration response with rub phenomenon was studied through bifurcation analysis over a wide range of speeds. This numerical analysis illustrated a good agreement with the experimental study in both cases studies. It was shown from the bifurcation analysis that the rotational speed has an essential effect on the rub response characteristics. The observed results have several characteristics and are concluded as follows:

  • When changing mass unbalance, the bifurcation diagrams exhibited a complex dynamic behavior, and the high nonlinearity of the rotor system was obvious as shown in experiments. It was clearly shown that the onset of contact at the large mass unbalance occurs earlier when compared with that at the small mass unbalance. Also, the impact starts with different responses in each case.

  • At the same mass unbalance value, changing the radial clearance showed different responses at the onset of the contact. In addition, it affected the resulting subharmonic and super harmonic frequency components as deduced from the experimental study.

  • It was noticed from the numerical results that 1 × harmonic component was the dominant harmonic in all cases studies which was also observed from the experimental results.

  • In addition, the study showed the coexisting and alternation of several whirling responses due to changing the initial conditions and system parameters.

This study contributes toward a better understanding of the effect of rotor system parameters on the response characteristics of lateral vibrations due to rotor–stator rubbing. In the practical machinery, care should be taken to keep the centrifugal forces within acceptable limits. Moreover, machine health monitoring practices should be applied for the purpose of early diagnosis of faults that cause excessive vibrations and may give rise to rotor–stator rubs. Hence, safe and reliable operation of rotating machinery can be achieved.