1 Introduction

This paper relates to the each servo system of the naval gun system, the Laser Weapon system, and the EOTS (Electro-Optical Tracking System) installed on a ship. Each servo system in the above systems precisely tracks the position of the target. The servo system of the equipment installed on the ship must have servo characteristics that respond well to step, ramp, and sinusoidal input commands. Over the past few decades the position controller consisted of a Type II servo system. Type I is that the steady-state error is zero in the step input command, and Type II is that the steady-state error is zero in the ramp input command. Observing the movement of the target on the ship, it includes all waveforms of step, ramp, and sinusoidal. Step command and ramp command are generated by the movement of the target, and sinusoidal command is generated by the ship motion. In particular, the ship motion has a sinusoidal motion of less than 0.2–0.5 Hz [1,2,3,4]. In the case of the Type II servo system that tracks the position of such a target, the step and ramp commands can be precisely tracked, but the sinusoidal command has many errors. Otherwise, the laser weapon system being studied recently requires a servo system that maintains the position tracking error of the sinusoidal type ship motion to the level of the ramp error in order to focus the energy on the moving target. This paper is about a position control servo system that responds well to driving commands, including step, ramp, and sinusoidal.

In this paper, a new PI controller suitable for a servo controller responding to sinusoidal driving commands is developed using a concept taken from Park’s transformation used in an AC motor’s current controller. This controller achieves the steady-state error of the sinusoidal to the steady-state error level of the ramp.

In this paper we convert the sinusoidal input command frequency into the synchronous frame frequency used in Park’s transformation. The controller is derived from using the relationship between the stationary frame regulator and the synchronous frame regulator studied in [5,6,7]. In order to detect the frequency required for conversion, FDB (Frequency Detection Block) was proposed.

In order to maintain the stability of the servo system, a position controller was constructed in parallel to the existing Type II servo controller by applying the proposed control rule. To apply the control rule, the control zone was divided into a fine zone and a coarse zone and the proposed controller applied only to the fine zone. The proposed controller can verify the results through simulation.

2 New servo controller design specialized for AC input command

2.1 AC input servo controller review using Park’s transformation

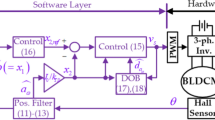
For the past several decades, the position controller of the servo system consists of multi-loop consisting of position loop, speed loop inside it, and current loop inside it. If the bandwidth of the current loop is much higher than that of the speed loop, and the bandwidth of the speed loop is much higher than that of the position loop, the transfer function of the current loop can be set to unity. And the speed loop can be described as a controller that can be included in the power converter in Fig. 1.

Fig. 1
figure 1

Servo control system

Full size image

In the servo control system of Fig. 1, if the control laws are composed of PI and the control input is set to sinusoidal frequency \(\omega_{i}\)(\(\omega_{i} = 2\pi (0.2\sim 0.5\,{\text{Hz)}}\), ship motion frequency), it is unsatisfactory because it has a serious steady-state error. If the input sinusoidal command frequency is known, the concept of Park’s transformation can be applied [5,6,7]. Park’s transformation converts AC sinusoidal input commands into DC quantities of a rotating frame to construct a controller, then the error can be made to zero. Park’s transformation is given as Eq. (1):

$$ \left[ {\begin{array}{*{20}c} {x_{{\text{d}}} } \\ {x_{{\text{q}}} } \\ \end{array} } \right] = T_{{{\text{dq}}}} \left[ {\begin{array}{*{20}c} {x_{\alpha } } \\ {x_{\beta } } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{\text{cos}}\theta } & {{\text{sin}}\theta } \\ { - {\text{sin}}\theta } & {{\text{cos}}\theta } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {x_{\alpha } } \\ {x_{\beta } } \\ \end{array} } \right] $$
(1)

where \(x_{\alpha } , x_{\beta }\) are the stator reference frame, and \(x_{{\text{d}}} , x_{{\text{q}}}\) are the rotor reference frame. \(T_{{{\text{dq}}}}\) is a transformation matrix. Equation (1) can be expressed by Eq. (2) using the complex phasor representation of the vector.

$$ \begin{aligned} \vec{x}_{{{\text{dq}}}} & = x_{{\text{d}}} + jx_{{\text{q}}} = x_{\alpha } \cos \theta + x_{\beta } \sin \theta \\ & \quad + j\left( { - x_{\alpha } \sin \theta + x_{\beta } \cos \theta } \right) \\ & = \left( {x_{\alpha } + jx_{\beta } } \right)\left( {\cos \theta - j\sin \theta } \right) \\ & = \vec{x}_{\alpha \beta } e^{ - j\theta } \\ \end{aligned} $$
(2)

The inverse of Eq. (2) is the same as Eq. (3).

$$ \vec{x}_{\alpha \beta } = \vec{x}_{{{\text{dq}}}} e^{j\theta } ,\quad \theta = \omega t $$
(3)

By applying the concepts of Eqs. (2) and (3), if the controller in the synchronous frame is configured as \(H_{{{\text{DC}}}} \left( s \right)\) and the controller converted into the stationary frame is configured as \(H_{{{\text{AC}}}} \left( s \right)\), the configuration as shown in Fig. 2 is possible.

Fig. 2
figure 2

Organization of the synchronous reference frame controller

Full size image

In Fig. 2, \(\vec{e}_{\alpha \beta }\) represents the sinusoidal error with \(\theta = \omega t\) component in the stator reference frame, when \(\vec{e}_{\alpha \beta }\) is a positive number, multiplying \(\vec{e}_{\alpha \beta }\) by \(e^{j\theta }\) results in a DC component \(\vec{e}_{\alpha \beta } e^{j\theta }\) corresponding to \(\theta = \omega t\) while changing to the rotator reference frame, which is input to the PI controller (\(H_{{{\text{DC}}}} \left( s \right)\)). In order to convert the output of the PI controller (\(H_{{{\text{DC}}}} (s)\)) into the stator reference frame, \(\vec{u}_{\alpha \beta }\) can be obtained by multiplying the inverse conversion operator \(e^{ - j\theta }\). When \(\vec{e}_{\alpha \beta }\) is negative, it is calculated by the bottom path of Fig. 2.

When the transfer function is obtained, the following relation is established:

$$ \frac{{\vec{u}_{\alpha \beta } \left( s \right)}}{{\vec{e}_{\alpha \beta } \left( s \right)}} = \frac{{\vec{u}_{\alpha \beta + } \left( s \right)}}{{\vec{e}_{\alpha \beta } \left( s \right)}} + \frac{{\vec{u}_{\alpha \beta - } \left( s \right)}}{{\vec{e}_{\alpha \beta } \left( s \right)}} = = 2K_{{\text{P}}} + \frac{{K_{{\text{I}}} \omega_{{\text{c}}} }}{{s + j\omega_{{\text{o}}} + \omega_{{\text{c}}} }} + \frac{{K_{{\text{I}}} \omega_{{\text{c}}} }}{{s - j\omega_{{\text{o}}} + \omega_{{\text{c}}} }} = 2K_{{\text{P}}} + \frac{{2K_{{\text{I}}} \omega_{{\text{c}}} s + 2K_{{\text{I}}} \omega_{{\text{c}}}^{2} }}{{s^{2} + 2\omega_{{\text{c}}} s + \omega_{{\text{o}}}^{2} + \omega_{{\text{c}}}^{2} }} $$
(4)

where \(\omega_{{\text{o}}}\) is the synchronous frequency, and \(\omega_{{\text{c}}}\) is the breakpoint frequency of the integral controller.

If assume \(\omega_{{\text{c}}} \ll \omega_{{\text{o}}}\), the Eq. (4) can be simplified into Eq. (5) [7].

$$ H_{{{\text{AC}}}} \left( s \right) = 2K_{{\text{P}}} + \frac{{2K_{{\text{I}}} \cdot \omega_{{\text{c}}} s}}{{s^{2} + 2\omega_{{\text{c}}} s + \omega_{{\text{o}}}^{2} }} $$
(5)

The transfer function of Eq. (5) has frequency response characteristic, as shown in Fig. 3. Each parameter of the Bode Diagram is \(K_{{\text{P}}} = 60\), \(K_{{\text{I}}} = 3623\), \(\omega_{{\text{o}}} = 3.14\,{\text{rad/s}}\), \(\omega_{{\text{c}}} = 0.157\;{\text{rad/s}}\). \(\omega_{{\text{o}}}\) is 0.5 Hz, which is the maximum frequency of ship motion, and \(\omega_{{\text{c}}}\) is 0.025 Hz, which is 5% of \(\omega_{{\text{o}}}\).

Fig. 3
figure 3

Bode Diagram of proposed AC controller Eq. (5)

Full size image

Figure 3 is the Bode Diagram of the stator reference frame compensator performed using the transfer function \(H_{{{\text{AC}}}} \left( s \right)\). The frequency scale is logarithmic, and the vertical scale is linear.

Angular velocity ranges from \(10^{ - 2} \,{\text{rad/s}}\) to \(10^{3} \,{\text{rad/s}}\). The size of the gain according to the angular velocity is 72[dB] at \(\omega_{{\text{o}}} = 3.14\,{\text{rad/s}}\), other than that, it is 42[dB]. The gain is the largest when the angular velocity we want (\(\omega_{{\text{o}}} = 3.14\,{\text{rad/s}}\)), and this gain keeps the sinusoidal error of the angular velocity (\(\omega_{{\text{o}}} = 3.14\,{\text{rad/s}}\)) at zero.

Figure 4 shows a new servo controller specialized for AC to which \(H_{{{\text{AC}}}} (s)\) is applied. If \(H_{{{\text{AC}}}} (s)\) achieves a relatively high gain at the synchronous frequency, then due to the performance of the controller, the steady-state error will be nearly zero.

Fig. 4
figure 4

A proposed servo controller specialized for AC

Full size image

2.2 Control method of proposed servo controller specialized for AC

In servo systems such as a ship-mounted gun system, the laser weapon system, and the EOTS (Electro-Optical Tracking System), the appearance of the target is approximated by a step position input, constant velocity flight is approximated by a ramp position input, and ship motion is approximated by a sinusoidal position input. The ship motion can be expressed as a sinusoidal of 0.2–0.5 Hz that changes every cycle [1,2,3,4].

As shown in Fig. 4, the proposed servo controller specialized for AC is a controller for compensating ship motion. It consists of control law Eq. (5) and FDB (Frequency Detection Block). FDB performs Discrete Fourier Transformation or Fast Fourier Transformation on servo system commands and errors. The sinusoidal component that is ship motion is extracted from the command. Then calculate the synchronous frequency \(\omega_{{\text{o}}}\) from the extracted sinusoidal. Also, the error magnitude, sinusoidal and driving direction are determined from the errors. This can be implemented in a digital signal processor (DSP) or a field programmable gate array (FPGA).

The calculated frequency \(\omega_{{\text{o}}}\) satisfies Eq. (6), and as shown in Fig. 5, after confirming that it is a fine zone in the control zone according to the position error size (mrad), this control law is applied only in the case of steady-state conditions.

$$ \omega_{{\text{o}}} + \omega_{{\text{c}}} < \omega_{{{\text{BW}}}} $$
(6)

where \(\omega_{{\text{c}}}\) is arbitrarily selected at the level of 5% of \(\omega_{{\text{o}}}\), and \(\omega_{{{\text{BW}}}}\) is the bandwidth frequency of the conventional control closed-loop in Fig. 10 Bode Diagram. \(\omega_{{\text{c}}}\) is the frequency selectivity of the controller and may reflect the frequency error calculated by the FDB. 5% is an arbitrarily selected frequency error reflection rate. Equation (6) is a frequency limit to ensure the stability of the controller, which will be explained in Sect. 3.2.

Fig. 5
figure 5

Classification of proposed AC control zone (fine zone) according to Position Error

Full size image

Figure 5 is a graph showing position error and control command (\(\omega_{i}\)). In order to distinguish the steady state according to the position error, a fine zone with a small error is identified, and the proposed controller operates in this zone.

3 Configuration and stability of servo controller

3.1 Configuration of servo controller

If the servo system is composed of a parallel combination of the Type II servo controller used for the past several decades and the proposed AC controller specialized for ac input designed here, the proposed position controller of the servo system can be configured as shown in Fig. 6. In the servo control system in Fig. 1, when the control zone is the fine zone, the transfer function of the power converter can be set as a unity, and the plant is assumed to be a motor control load. In Fig. 6, the conventional controller’s transfer function TC(s) is the same as Eq. (7), and it is a Type II servo controller.

$$ T_{{\text{C}}} \left( s \right) = \frac{{\left( {bK_{{\text{F}}} + bK_{{\text{D}}} } \right)s + bK_{{\text{P}}} }}{{s^{2} + \left( {a + bK_{{\text{D}}} } \right)s + bK_{{\text{P}}} }} $$
(7)
Fig. 6
figure 6

Block Diagram of the proposed position controller

Full size image

To select the values of each coefficient in Eq. (7), applying the optimum coefficients of the transfer function corresponding to the ITAE criterion-based ramp input to Eq. (7), then the transfer function T(s) is the same as Eq. (8) [8]. By comparing Eq. (8) with Eq. (7) with the coefficients, each parameter (\(K_{{\text{P}}} , K_{{\text{D}}} , K_{{\text{F}}}\)) of the controller can be determined.

$$ T\left( s \right) = \frac{{3.2\omega_{n} s + \omega_{n}^{2} }}{{s^{2} + 3.2\omega_{n} s + \omega_{n}^{2} }} $$
(8)

We make the proposed AC controller's integral gain \(K_{{{\text{I}}\_{\text{ac}}}}\) large enough to essentially eliminate all steady-state errors. The larger the proportional gain \(K_{P\_ac}\), the faster the transient response, so adjust it until overshoot.

3.2 Stability of Servo controller

To measure the stability of the proposed AC controller and the proposed position controller, we measure gain margin and phase margin using open-loop Bode Diagram.

Looking at the open-loop Bode Diagram of the proposed AC controller in Fig. 7, the gain margin is infinite, and the phase margin is 42.8° at a frequency of 2 Hz (12.7 rad/s). It can be seen that resonance occurs at 0.5 Hz (3.14 rad/s). The gain parameters of the Bode Diagram are the same as in the case of Fig. 3, after that the plant of all simulations is the same as Eq. (9).

Fig. 7
figure 7

Open-loop Bode Diagram of the proposed AC controller

Full size image

Figure 8 is an open-loop Bode Diagram of the proposed position controller (conventional controller + proposed AC controller) in Fig. 6, and the frequency of the AC controller is 0.5 Hz (maximum frequency of ship motion). The gain margin is infinite, and the phase plot shows a phase margin of over 125° at 2.6 Hz, so the system is definitely stable. The introduction of the proposed AC controller radically changes the Bode Diagram at the resonant frequency, but it has little effect on the crossover frequency of the conventional controller parameters. Therefore, since the phase delay is less than 180°, the proposed AC controller remains stable below the crossover frequency.

Fig. 8
figure 8

Open-loop Bode Diagram of the proposed controller (conventional controller + proposed AC controller)

Full size image

Figure 9 compares the closed-loop Bode Diagram of the conventional controller, which is a stable system, and the open-loop Bode Diagram of the proposed position controller (the conventional controller + the proposed AC controller). It can be seen that the gain of the proposed position controller forms the same gain as that of the conventional controller from before the cut-off frequency of the closed-loop conventional controller.

Fig. 9
figure 9

Closed-loop Bode Diagram of the conventional controller, Open-loop Bode Diagram of proposed position controller (conventional controller with proposed AC controller)

Full size image

As a result, if the \(\omega_{{\text{o}}}\) of the proposed AC controller is not larger than the bandwidth of the conventional controller and is a nearby value, and there is no gain reduction due to the gain peaking, the system is maintained stably. If the frequency is limited by \(\omega_{{\text{c}}}\) to avoid the gain peaking, Eq. (4) holds. Here, \(\omega_{{\text{c}}}\) was selected as 5% of \(\omega_{{\text{o}}}\).

Figure 10 is a closed-loop Bode Diagram to check the bandwidth and gain peaking of a conventional controller. The band width frequency of the conventional controller is 5.6 Hz (35.4 rad/s), and gain peaking does not appear.

Fig. 10
figure 10

Closed-loop Bode Diagram of the conventional controller

Full size image

4 Simulation results

We analyzed the dynamic characteristics of the position controller for step, ramp, and sinusoidal commands using the computer simulation and confirmed the steady-state error and the results are shown in Figs. 11, 12, 13 and 14.

Fig. 11
figure 11

Output response to step input of the proposed position controller

Full size image
Fig. 12
figure 12

Position error to ramp input (10°/s) of the proposed position controller

Full size image
Fig. 13
figure 13

Position error to sinusoidal input (5°sin(3.14t)) of the conventional controller and the proposed position controller

Full size image
Fig. 14
figure 14

Position error to sinusoidal input (30°sin(1.256t)) of the conventional controller and the proposed position controller

Full size image

In order to simulate this controller, the plant is assumed to be Eq. (9), and the natural frequency of the servo system is assumed to be Eq. (10).

$$ G_{{\text{p}}} \left( s \right) = \frac{b}{{s\left( {s + a} \right)}} = \frac{5.23}{{s\left( {s + 65} \right)}} $$
(9)
$$ \omega_{{\text{n}}} = \sqrt {bK_{{\text{P}}} } = 25\,{\text{rad/sec}} $$
(10)

Figure 11 is the position output waveform for the step input. There is about 10% overshoot and converges to the steady-state after 0.5 s.

As it is a step command, the proposed AC controller does not work; only the conventional controller works.

Figure 12 shows the position error for the ramp input (10°/s), and the position error converges to a steady-state condition with less than 0.01 mrad after 0.5 s. Only conventional controller works.

Figure 13 is a position error waveform for sinusoidal input 5°sin (3.14t). The position error of the conventional controller is 2.13 mrad and the position error of the proposed position controller is less than 0.069 mrad, which both controllers are controlled in the fine zone (3 mrad or less). And the repetitive controller is 0.92 mrad, as shown in Table 1. Compared to each other, it can be seen that the steady-state control accuracy of the proposed position controller is improved 50 times that of the conventional controller and 13 times that of the repetitive controller.

Table 1 Position Error of sinusoidal input of the convention controller and the proposed controller
Full size table

Figure 14 is a position error waveform for sinusoidal input 30°sin (1.256t). It can be seen that the position error of the proposed position controller is controlled to less than 0.065 mrad after 0.5 s.

Figure 15 shows the repetitive controller proposed in [9].

Fig. 15
figure 15

Repetitive controller proposed in [9]

Full size image

As shown in Fig. 15, the proposed repetitive controller is formed by the following blocks:

  • A generic delay “\(e^{{ - T_{1} s/n}}\)”: The use of a periodic signal generator formed by generic delay makes possible to compensate harmonics components in the family (\(nk,\quad k \in Z\));

  • A complex gain “\(e^{j\theta }\)”: When implementing a complex gain inside of the periodic signal generator, it allows to shift the frequency response of the controller. Thus, when used along to the generic delay, it is possible to select a harmonic m so that the controller compensates the family (\(nk + m,\quad k \in Z\)) [9].

A repetitive controller is a control algorithm that can track a periodic reference signal and has been recently studied [10,11,12,13].

Figure 16 shows that the position controller is configured by applying the repetitive controller. Using this controller, the position error for the sinusoidal position command was simulated by a computer.

Fig. 16
figure 16

Position controller with repetitive controller

Full size image

Table 1 shows positional errors by amplitude and frequency of sinusoidal input of the conventional controller, repetitive controller, and proposed position controller. The unit of error is milliradian.

The proposed position controller shows the good performance at the amplitude and frequency of all sinusoidal compared to the repetitive controller. Conventional controller shows that the position error increases significantly as the amplitude and frequency increase.

5 Conclusion

In this paper, we propose a controller that can demonstrate the good performance by controlling the steady-state error for sinusoidal commands in a servo system in which step, ramp, and sinusoidal commands are mixed.

In servo systems developed in Type I and Type II, residual errors occur in sinusoidal commands. The proposed controller is a new controller without steady-state errors of sinusoidal commands.

The proposed controller transforms the sinusoidal command into a synchronous frame method based on Park's transformation theory. Through this, “the AC control law” equivalent to PI control at DC input was completed.

The key to control lies in accurate frequency detection and accurate steady-state determination in a frequency detection block (FDB). In this paper, for frequency detection, the frequencies of the command signal and the error signal were detected by using the timer of a digital signal processor (DSP), and the steady-state condition was performed in the fine zone, a precision control section, by dividing the control zone according to the error size. Since the proposed AC controller is added in parallel to the existing stable Type II servo system, the proposed position controller has no major problem with stability, and the stability condition has been proven. We confirmed that the proposed controller has the good performance compared to the repetitive controller.