Skip to main content
SpringerLink
Log in

Convergence and stability of the split-step composite \(\theta \)-Milstein method for stochastic delay differential equations

  • Published:
International Journal of Dynamics and Control Aims and scope Submit manuscript

Abstract

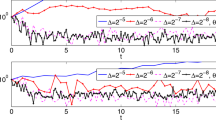
This research analyzes split-step composite \(\theta \)-Milstein (SSCTM) method based on stochastic delay differential equations, with particular focuses on examining its convergence and stability. We prove SSCTM method converges with strong order 1. Sufficient conditions for stability are given. Further, the regions in which SSCTM method exhibits stability are investigated. Numerical simulations validate our theoretical part.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

Data availability

No data was used for the research described in the article.

References

  1. Mao X, Yuan C, Zou J (2005) Stochastic differential delay equations of population dynamics. J Math Anal Appl 304:296–320

    Article  MathSciNet  Google Scholar 

  2. Dung NT (2013) Fractional stochastic differential equations with applications to finance. J Math Anal Appl 397:334–348

    Article  MathSciNet  Google Scholar 

  3. Tian T, Burrage K, Burrage P et al (2007) Stochastic delay differential equations for genetic regulatory networks. J Comput Appl Math 205(2):696–707

    Article  MathSciNet  Google Scholar 

  4. Beretta E, Kolmanovskii V, Shaikhet L (1998) Stability of epidemic model with time delays influenced by stochastic perturbations. Math Comput Simlat 45(3–4):269–277

    Article  MathSciNet  Google Scholar 

  5. Shi J (2015) Optimal control for stochastic differential delay equations with Poisson jumps and applications. Random Oper Stoch Equ 23(1):39–52

    Article  MathSciNet  Google Scholar 

  6. Mao X (2007) Exponential stability of equidistant Euler-maruyama approximations of stochastic differential delay equations. J Comput Appl Math 200:297–316

    Article  MathSciNet  Google Scholar 

  7. Küchler U, Platen E (2000) Strong discrete time approximation of stochastic differential equations with time delay. Math Comput Simulat 54:189–205

    Article  MathSciNet  Google Scholar 

  8. Baker CTH, Buckwar E (2000) Numerical analysis of explicit one-step methods for stochastic delay differential equations. LMS J Comput Math 3:315–335

    Article  MathSciNet  Google Scholar 

  9. Baker CTH, Buckwar E (2005) Exponential stability in p-th mean of solutions and of convergent Euler-type solutions of stochastic delay differential equations. J Comput Appl Math 184:404–427

    Article  MathSciNet  Google Scholar 

  10. Zong X, Wu F, Huang C (2015) Theta schemes for SDDEs with non-globally Lipschitz continuous coefficients. J Comput Appl 278:58–277

    Article  MathSciNet  Google Scholar 

  11. Hu Y, Mohammed SA, Yan F (2004) Discrete-time approximations of stochastic delay equations: the Milstein scheme. Ann Probab 32:265–314

    Article  MathSciNet  Google Scholar 

  12. Mattingly JC, Stuart AM, Higham DJ (2002) Ergodicity for SDEs and approximations: locally Lipschitz vector fields and degenerate noise. Stoch Process Appl 101(2):185–232

    Article  MathSciNet  Google Scholar 

  13. Higham DJ, Mao X, Stuart AM (2002) Strong convergence of Euler-type methods for nonlinear stochastic differential equations. SIAM J Numer Anal 40(3):1041–1063

    Article  MathSciNet  Google Scholar 

  14. Zhang H, Gan S, Hu L (2008) The split-step backward Euler method for linear stochastic delay differential equations. J Comput Appl Math 225(2):558–568

    Article  MathSciNet  Google Scholar 

  15. Guo Q, Xie W, Tao X et al (2012) Convergence of split-step Milstein method for linear stochastic delay differential equations. Commun Appl Math Comput 26(04):456–464

    MathSciNet  Google Scholar 

  16. Ding X, Ma Q, Zhang L (2010) Convergence and stability of the split-step \(\theta \)-method for stochastic differential equations. Comput Math Appl 60(5):1310–1321

    Article  MathSciNet  Google Scholar 

  17. Cao W, Hao P, Zhang Z (2014) Split-step \(\theta \)-method for stochastic delay differential equations. Appl Numer Math 76:19–33

    Article  MathSciNet  Google Scholar 

  18. Rouz OF, Ahmadian D, Milev M (2017) Exponential mean-square stability of two classes of theta Milstein methods for stochastic delay differential equations. AIP Conf Proc 1910:60015–60015

    Article  Google Scholar 

  19. Guo Q, Li H, Zhu Y (2014) The improved split-step \(\theta \) methods for stochastic differential equation. Math Method Appl 37(15):2245–2256

    Article  MathSciNet  Google Scholar 

  20. Zhang Z, Zhang E, Li L (2022) The improved stability analysis of numerical method for stochastic delay differential equations. Mathematics 10(18):3366

    Article  Google Scholar 

  21. Zhou L, Zhang J, Wang H (2007) Convergence of the composite \(\theta \)-method for a linear stochastic differential delay equation. J HLJU 06:778–783

    Google Scholar 

  22. Buckwar E (2000) Introduction to the numerical analysis of stochastic delay differential equations. J Comput Appl Math 125:297–307

    Article  MathSciNet  Google Scholar 

  23. Reshniak V, Khaliq AQM, Voss DA (2015) Split-step Milstein methods for multi-channel stiff stochastic differential systems. Appl Numer Math 89:1–23

    Article  MathSciNet  Google Scholar 

  24. Singh S (2012) Split-step forward Milstein method for stochastic differential equation. Int J Numer Anal Mod 9(4):970–981

    MathSciNet  Google Scholar 

  25. Mao X (2007) Stochastic differential equations and applications. Elsevier

    Google Scholar 

  26. Liu M, Cao W, Fan Z (2004) Convergence and stability of the semi-implicit Euler method for a linear stochastic differential delay equation. J Comput Appl Math 170(2):255–268

    Article  MathSciNet  Google Scholar 

  27. Kloeden PE, Platen E (1992) Numerical solution of stochastic differential equations. Springer, Berlin

    Book  Google Scholar 

Download references

Funding

This work was supported by the [National Natural Science Foundation of China] under Grant [Numbers 61763008, 71762008, 62166015]; and the [Guangxi Science and Technology Planning Project] under Grant [Numbers 2018GXNSFAA294131, 2018GXNSFAA050005].

Author information

Authors and Affiliations

  1. School of Science, Guilin University of Technology, Guilin, 541006, Guangxi, China

    Yuanqiao Lu, Haomin Zhang & Songyu Hong

  2. Guangxi Colleges and Universities Key Laboratory of Applied Statistics, Guilin University of Technology, Guilin, 541000, Guangxi, China

    Haomin Zhang

Authors
  1. Yuanqiao Lu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Haomin Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Songyu Hong
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

YL contributed to conceptualization, methodology, software, formal analysis, writing—original draft, and writing—review and editing; HZ contributed to validation, writing—review and editing, supervision, project administration, and funding acquisition; SH contributed to investigation and visualization.

Corresponding author

Correspondence to Haomin Zhang.

Ethics declarations

Conflict of interest

The authors declare they have no financial interests.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lu, Y., Zhang, H. & Hong, S. Convergence and stability of the split-step composite \(\theta \)-Milstein method for stochastic delay differential equations. Int. J. Dynam. Control 12, 1302–1313 (2024). https://doi.org/10.1007/s40435-023-01253-y

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40435-023-01253-y

Keywords

Search

Navigation