Skip to main content
SpringerLink
Log in

Fibonacci wavelets-based numerical method for solving fractional order (1 + 1)-dimensional dispersive partial differential equation

  • Published:
International Journal of Dynamics and Control Aims and scope Submit manuscript

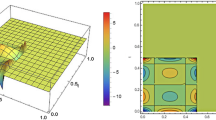
Abstract

In this study, third-order fractional (1 + 1)-dimensional dispersive partial differential equations are numerically solved using the generalized fractional-order Fibonacci wavelet functions. Fibonacci wavelet functions and functional integration matrices are intended to be used. Firstly, we constructed the functional matrix of the Fibonacci wavelets. Secondly, we developed a new technique called the Fibonacci wavelet collocation scheme (FWCS) to solve the fractional partial differential equations (FPDEs). Here, we transform the considered FPDEs into a system of algebraic equations using properties of the Fibonacci wavelets and their matrices. The Newton–Raphson method/fsolve command in MATLAB is used to solve the given system of algebraic equations to determine the unknown coefficients. The projected Fibonacci wavelet collocation method (FWCM) applicability, validity, and accuracy are illustrated with numerical examples. We also discuss the convergence analysis through the theorems and the error bound of the current technique. We execute the vital role of the wavelets, and the proposed method is far better than other methods in the literature through tables.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

Data availability

The data supporting this study's findings are available within the article.

Code availability

Mathematica code for finding the functional matrix of integration is available in the manuscript.

References

  1. Al-Refai M, Luchko Y (2014) Maximum principle for the fractional diffusion equations with the Riemann–Liouville fractional derivative and its applications. Fract Calc Appl Anal 17(2):483–498

    MathSciNet  MATH  Google Scholar 

  2. Bazhlekova E, Bazhlekov I (2014) Viscoelastic flows with fractional derivative models: computational approach by convolutional calculus of Dimovski. Fract Calc Appl Anal 17(4):954–976

    MathSciNet  MATH  Google Scholar 

  3. Liu Z, Li X (2015) Approximate controllability of fractional evolution systems with Riemann–Liouville fractional derivatives. SIAM J Control Optim 53(4):1920–1933

    MathSciNet  MATH  Google Scholar 

  4. Atangana A, Baleanu D (2016) New fractional derivatives with the nonlocal and non-singular kernel: theory and application to heat transfer model. Therm Sci 20(2):763–769

    Google Scholar 

  5. Caputo M, Fabrizio M (2015) A new definition of fractional derivative without singular kernel. Prog Fract Differ Appl 1(2):73–85

    Google Scholar 

  6. Rekhviashvili S, Pskhu A, Agarwal P, Jain S (2019) Application of the fractional oscillator model to describe damped vibrations. Turk J Phys 43(3):236–242

    Google Scholar 

  7. Agarwal P, Jain S (2011) Further results on fractional calculus of Srivastava polynomials. Bull Math Anal Appl 3(2):167–174

    MathSciNet  MATH  Google Scholar 

  8. Agarwal P, Baltaeva U, Alikulov Y (2020) Solvability of the boundary-value problem for a linear loaded integrodifferential equation in an infinite three-dimensional domain. Chaos Solitons Fractals 140:110108

    MathSciNet  MATH  Google Scholar 

  9. Agarwal P, Jain S, Agarwal S, Nagpal M (2014) On a new class of integrals involving Bessel functions of the first kind. Commun Numer Anal 2014:1–7

    MathSciNet  Google Scholar 

  10. Hilfer R (2000) Applications of fractional calculus in physics. Singapore, World Scientific Company

  11. Caputo M (1967) Linear models of dissipation whose Q is almost frequency independent-II. Geophys J Roy Astron Soc 13:529–539

    Google Scholar 

  12. Deshpande A, Daftardar-Gejji V (2016) Chaos in discrete fractional difference equations. Pramana 87:1–10

    MATH  Google Scholar 

  13. Fang L, Liu J, Ju S, Zheng F, Dong W, Shen M (2010) Experimental and theoretical evidence of enhanced ferromagnetism in sonochemical synthesized BiFeO3 nanoparticles. Appl Phys Lett 97:242501

    Google Scholar 

  14. Shah NA, Dassios I, Chung JD (2021) Numerical investigation of time-fractional equivalent width equations that describe hydromagnetic waves. Symmetry 13:418

    Google Scholar 

  15. Miller KS, Ross B (1993) An introduction to fractional calculus and fractional differential equations. Wiley, New York, NY, USA

    MATH  Google Scholar 

  16. Kilbas AA, Srivastava HM, Trujillo JJ (2006) Theory and applications of fractional differential equations. Elsevier, Amsterdam, The Netherlands

    MATH  Google Scholar 

  17. Gupta S, Ranta S (2022) Legendre wavelet-based numerical approach for solving a fractional eigenvalue problem. Chaos Solitons Fractals 155:111647

    MathSciNet  MATH  Google Scholar 

  18. Rehman MU, Baleanu D, Alzabut J, Ismail M (2020) Saeed U (2020) Green–Haar wavelets method for generalized fractional differential equations. Adv Differ Equ 1:515

    MATH  Google Scholar 

  19. Faheem M, Khan A, Oruç Ö (2022) A generalized Gegenbauer wavelet collocation method for solving p-type fractional neutral delay differential and delay partial differential equations. Math Sci

  20. Kumbinarasaiah S (2022) A novel approach for multi-dimensional fractional coupled Navier–Stokes equation. SeMA

  21. Kumbinarasaiah S (2021) Hermite wavelets approach for the multi-term fractional differential equations. J Interdiscip Math 4(5):1241–1262

    Google Scholar 

  22. Dehestani H, Ordokhani Y, Razzaghi M (2022) Modified wavelet method for solving multitype variable-order fractional partial differential equations generated from the modeling of phenomena. Math Sci 16:343–359

    MathSciNet  MATH  Google Scholar 

  23. Zhu L, Wang Y (2017) Solving fractional partial differential equations by using the second Chebyshev wavelet operational matrix method. Nonlinear Dyn 89(3):1915–1925

    MathSciNet  Google Scholar 

  24. Aruldoss R, Devi RA, Krishna PM (2021) An expeditious wavelet-based numerical scheme for solving fractional differential equations. Comput Appl Math 40(1):2

    MathSciNet  MATH  Google Scholar 

  25. Alrabaiah H, Ahmad I, Amin R, Shah K (2022) A numerical method for fractional variable order pantograph differential equations based on Haar wavelet. Eng Comput 38:2655–2668

    Google Scholar 

  26. Kumar S, Kumar R, Osman MS, Samet BA (2021) wavelet based numerical scheme for fractional order SEIR epidemic of measles by using Genocchi polynomials. Numer Methods Partial Differ Equ 37:1250–1268

    MathSciNet  Google Scholar 

  27. Aminikhah H, Tahmasebi M, Roozbahani MM (2016) Numerical solution for the time–space fractional partial differential equations by using the wavelet multi–scale method. UPB Sci Bull Ser A 78(4):175–188

    MathSciNet  MATH  Google Scholar 

  28. Aghazadeh N, Mohammadi A, Ahmadnezhad G, Rezapour S (2021) Solving partial fractional differential equations by using the Laguerre wavelet-Adomian method. Adv Differ Equ 2021:231

    MathSciNet  MATH  Google Scholar 

  29. Toan PT, Vo TN, Razzaghi M (2021) Taylor wavelet method for fractional delay differential equations. Eng Comput 37:231–240

    Google Scholar 

  30. Kumbinarasaiah S, Mulimani M (2022) A novel scheme for the hyperbolic partial differential equation through Fibonacci wavelets. J Taibah Univ Sci 16(1):1112–1132

    Google Scholar 

  31. Sabermahani S, Ordokhani Y, Yousefi S (2020) Fibonacci wavelets and their applications for solving two classes of time-varying delay problems. Optim Control Appl Methods 41:395–416

    MathSciNet  MATH  Google Scholar 

  32. Irfan M, Shah FA, Nisar KS (2021) Fibonacci wavelet method for solving Pennes bioheat transfer equation. Int J Wavelets Multiresolution and Inf Process 19(6):2150023

    MathSciNet  MATH  Google Scholar 

  33. Shah FA, Irfan M, Nisar KS, Matoog RT, Mahmoud EE (2021) Fibonacci wavelet method for solving time-fractional telegraph equations with Dirichlet boundary conditions. Results Phys 24:104123

    Google Scholar 

  34. Irfan M, Shah FA (2021) Fibonacci wavelet method for solving the time-fractional bioheat transfer model. Optik 241:167084

    Google Scholar 

  35. Sabermahani S, Ordokhani Y (2021) Fibonacci wavelets and Galerkin method to investigate fractional optimal control problems with bibliometric analysis. J Vib Control 27(15–16):1778–1792

    MathSciNet  Google Scholar 

  36. Düşünceli F, Çelik E (2017) Fibonacci matrix polynomial method for linear complex differential equations. Asian J Math Comput Res 15:229–238

    Google Scholar 

  37. Koc AB, Cakmak M, Kurnaz A (2014) A matrix method based on the Fibonacci polynomials to the generalized pantograph equations with functional arguments. Adv Math Phys 2014:694580

    MATH  Google Scholar 

  38. Abd-Elhameed WM, Youssri YH (2019) Spectral tau algorithm for certain coupled system of fractional differential equations via generalized Fibonacci polynomial sequence. Iran J Sci Technol Trans Sci 43:543–554

    MathSciNet  Google Scholar 

  39. Atta AG, Moatimid GM, Youssri YH (2020) Generalized Fibonacci operational tau algorithm for fractional Bagley–Torvik Equation. Progress Fract Differ Appl 6:215–224

    Google Scholar 

  40. Youssri YH (2022) Two Fibonacci operational matrix pseudo-spectral schemes for nonlinear fractional Klein–Gordon equation. Int J Mod Phys C 33:2250049

    MathSciNet  Google Scholar 

  41. Abd-Elhameed WM, Youssri YH (2016) A novel operational matrix of caputo fractional derivatives of Fibonacci polynomials: spectral solutions of fractional differential equations. Entropy 18(10):345

    MathSciNet  Google Scholar 

  42. Youssri YH, Abd-Elhameed WM (2016) Spectral solutions for multi-term fractional initial value problems using a new fibonacci operational matrix of fractional integration. Progress Fract Differ Appl 2:141–151

    Google Scholar 

  43. Atta AG, Moatimid GM, Youssri YH (2019) Generalized Fibonacci operational collocation approach for fractional initial value problems. Int J Appl Comput Math 5(1):9

    MathSciNet  MATH  Google Scholar 

  44. Koshy T (2018) Fibonacci and lucas numbers with applications. Wiley, New York

    MATH  Google Scholar 

  45. Verma V, Prakash A, Kumar D, Singh J (2019) Numerical study of a fractional model of multi-dimensional dispersive partial differential equation. J Ocean Eng Sci 4:338–351

    Google Scholar 

  46. Djidjeli K, Twizell EH (1991) Global extrapolations of numerical methods for solving a third-order dispersive partial differential equation. Int J Comput Math 41(1–2):81–89

    MATH  Google Scholar 

  47. Kumbinarasaiah S (2021) Novel functional matrix method using standard basis of polynomial linear space. Int J Appl Comput Math 7:152

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors are grateful to the referees and the editor for carefully checking the details and for helpful comments that improved this paper. The author thanks the University Grants Commission (UGC), Govt. of India, for financial support under the UGC-BSR Research Start-Up Grant for 2021-2024:F.30-580/2021(BSR) Dated: 23rd Nov. 2021.

Funding

The authors state that no funding is involved.

Author information

Authors and Affiliations

  1. Department of Mathematics, Bangalore University, Bengaluru, India

    S. Kumbinarasaiah & Mallanagoud Mulimani

Authors
  1. S. Kumbinarasaiah
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Mallanagoud Mulimani
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

KS proposed the main idea of this paper. KS and MM prepared the manuscript and performed all the steps of the proofs in this research. Both authors contributed equally and significantly to writing this paper. Both authors read and approved the final manuscript.

Corresponding author

Correspondence to S. Kumbinarasaiah.

Ethics declarations

Conflict of interest

The authors have no competing interests to declare that are relevant to the content of this article.

Appendices

Algorithm to obtain Fibonacci wavelet coefficients and solution

Step 1 Compute Fibonacci wavelet basis using Eq. (2.2).

Step 2 Evaluate the functional matrix of integration for the desired order.

Step 3 Consider Eq. (4.3) depending upon the order of the selected PDE (4.1).

Step 4 Integrate Eq. (4.3) and obtain the required partial derivatives \(V,{V}_{t},{V}_{x},{V}_{xx}\) and \({V}_{xxx}\).

Step 5 Fit the obtained derivatives \(V,{V}_{t},{V}_{x},{V}_{xx}\) and \({V}_{xxx}\) in Eq. (4.1).

Step 6 Now, collocate Eq. (4.1) from the collocation points given in Eq. (4.12) and obtain the algebraic equations.

Step 7 Solve a set of algebraic equations using the fsolve command in MATLAB or Newton Raphson Method to obtain the unknown coefficients.

Step 8 Substitute the unknown coefficients in the Eq. (4.10) to find the FWCS solution.

Mathematica code for finding the functional matrix of integration up to the fourth integration

figure a
figure b

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kumbinarasaiah, S., Mulimani, M. Fibonacci wavelets-based numerical method for solving fractional order (1 + 1)-dimensional dispersive partial differential equation. Int. J. Dynam. Control 11, 2232–2255 (2023). https://doi.org/10.1007/s40435-023-01129-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40435-023-01129-1

Keywords

Search

Navigation