Simulation-based usability testing of some tracking controllers for underactuated underwater vehicles using simplified criteria

Abstract

This paper proposes a method for the preliminary verification of known control algorithms designed for tracking the desired trajectory of underactuated underwater vehicles. It is based on simplified criteria for the selection of suitable controllers. Moreover, a certain method for the selection of controller parameters is indicated, which can be effective in the initial analysis of the suitability of selected control schemes. In order to demonstrate the possible application of the described approach, several control strategies known from the literature were selected and numerical tests for them were performed for two 3 DOF models of underwater vehicles with different dynamics. The method given here can be useful for simulation studies at the stage of controller selection without its experimental validation.

1 Introduction

Autonomous underwater vehicle (AUV) are very popular among researchers because of their potential applications many researchers in in marine science, maritime security and navy. Moreover, they guarantee maneuvering precision, independent operating time of the vehicle.

There are many control algorithms that have been applied for ships, surface and underwater vehicles. Sometimes for a vehicle with known parameters or when the vehicle is at the design stage instead of developing a new control algorithm, one can check the usefulness of well-known algorithms from the literature. In this work an attempt was made to apply the already existing control strategies for the selected desired trajectory and two underwater vehicles moving in the horizontal plane. It is worth recalling just some of the controllers relating to the task of tracking the trajectory of marine vehicles. Very often backstepping techniques were applied for marine vehicles, e.g. [1,2,3]. However, in order to improve the performance of the controller this method was used together with the SMC (sliding mode control), e.g. [4, 5], backstepping technique and Lyapunov’s direct method [6, 7], backstepping and integral SMC [8], backstepping technique based on proportional integral (PI) sliding mode control [9], backstepping with active disturbance rejection control [10] or an output feedback control applying linear stability theory and backstepping technique [11]. The SMC algorithms were also proposed for underactuated underwater and surface vehicles many times, for example in [12, 13]. Sometimes they are applied with other control algorithms as PID-SMC [14, 15]. Another strategy applied to underwater vehicles was terminal sliding mode control (TSMC) algorithm [16]. The next group of control strategies are methods based on neural networks (NN). This approach is often based on a combination of different methods as shown, e.g. in [17] (NN and SMC), [18] (NN and TSMC), [19] (NN, barrier Lyapunov function, and backstepping algorithm), [20] (NN, backstepping, and SMC), [21] (NN, backstepping, and low-frequency techniques), [22] (NN control with extended state observer (ESO)), [23] (neural network and backstepping). For trajectory tracking also fuzzy logic based algorithms were used, for example fuzzy control algorithm [24], combination of SMC with an adaptive fuzzy control, backstepping method and the Lyapunov stability theory [25] or fuzzy neural approach [26]. Some other control strategies known from the literature are Dynamic Surface Control (DSC) method [27], prescribed performance approach for surface vehicles [28], modified inversion method [29], extension the control concept for unmanned ground vehicles to marine vehicles [30], bounded feedback based control scheme [31] or the event-triggered dynamic surface control [32].

The goal of the work is to propose an initial numerical test of selected known control algorithms that perform the task of tracking a circular trajectory (due to its popularity in the verification of control algorithms) for arbitrarily adopted two underactuated vehicle models. This approach is based on the assumption that the parameters of the controller should be selected intuitively to avoid the need to use additional optimization methods. In order to support this process, the procedure of selecting these parameters was presented, consisting in grouping those parameters that fulfill the same functions. Therefore, only such tracking control algorithms were taken into account for which the intuitive selection of parameters in the source work turned out to be sufficient or for which the use of additional tuning methods was not mentioned. The motivation to consider this problem is the emerging need to apply an appropriate control algorithm that guarantees acceptable tracking results for the desired trajectory. Once the underwater vehicle model is known, the next task is to use the controller. This can be done in two ways: develop own control scheme or adapt one or more control algorithms known from the literature. This work relates to the latter proposition. For this purpose, five known control strategies were compared, namely three intended strictly for underwater vehicles, one developed for ships and one dedicated to the control of an underactuated hovercraft. The presented approach is relevant prior to in-depth studies of the suitability of control algorithms using simulation without experimental validation. At this stage, it is necessary to decide whether it is worth carrying out an experiment on a real object using the selected controller, or to design or select a different control algorithm.

The contributions of this work can be summarized as follows:

• (1) proposing a simplified procedure for testing algorithms in order to assess their suitability for control of underwater vehicles selected using some defined criteria;

• (2) describing a method to facilitate the selection of control parameters that involves grouping parameters that serve the same purpose and applying it to parameter tuning in controllers;

• (3) simulation verification of selected control algorithms suitable for underactuated underwater vehicles for a circular trajectory and for two vehicle models to verify the effectiveness of these algorithms;

• (4) comparative analysis of the obtained simulation results and on the basis of the adopted formal criteria and making decisions on the selection of control algorithms that correctly perform the trajectory tracking task.

The reminder of this article is organized as follows. In Sect. 2 two kinds of the equations of motion, one for an underwater vehicle and one for a hovercraft are given. In Sect. 3, the selected tracking control algorithms are presented in a short form. In Sect. 4 simulations are performed to show effectiveness each of the proposed control strategy. Finally, conclusions are drawn in Sect. 5.

2 Underwater vehicle models

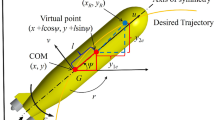
The considered model of an underwater vehicle moving horizontally is shown Figure 1.

Fig. 1

Underwater vehicle model sketch

At this stage, i.e. a preliminary investigation of the usefulness of selected control schemes, we skip the vehicle structure (due to the drive). For this reason, it is assumed that the friction forces or environmental disturbances are omitted what leads to simplification of the vehicle model. However, because the model is applicable for controlling a vehicle of a different construction, the equations corresponding to it are given separately.

Vehicle model with propellers (VMP). The vehicle model used for the test was described, e.g. in [4, 29]. For horizontal motion of the vehicle the kinematic and dynamic equations can be given in the following form:

$$\begin{aligned}&\dot{x}=u \cos \psi - v \sin \psi , \end{aligned}$$

(1)

$$\begin{aligned}&\dot{y}=u \sin \psi + v \cos \psi , \end{aligned}$$

(2)

$$\begin{aligned}&\dot{\psi }= r, \end{aligned}$$

(3)

$$\begin{aligned}&\dot{u} = \frac{m_{2}}{m_{1}}v r -\frac{d_{u}}{m_{1}} u + \frac{\tau _u}{m_{1}}, \end{aligned}$$

(4)

$$\begin{aligned}&\dot{v} = -\frac{m_{1}}{m_{2}}u r -\frac{d_{v}}{m_{2}} v, \end{aligned}$$

(5)

$$\begin{aligned}&\dot{r} = \frac{m_{1}-m_{2}}{m_{3}}u v -\frac{d_{r}}{m_{3}} r + \frac{\tau _r}{m_{3}}, \end{aligned}$$

(6)

where $\tau _u$, $\tau _r$ are the surge force and the yaw torque, respectively. The used symbols mean $m_1=m-X_{\dot{u}}$, $m_2=m-Y_{\dot{v}}$, and $m_3=J-N_{\dot{r}}$ (the mass and the appropriate added mass). In equations (1)-(6) u, v are linear velocities of x and y axis, respectively, r is angular velocity, m is the mass, J is the inertia, $d_u, d_v, d_r$ are the drag coefficients are assumed with sign $+$, e.g. in [4, 31] or −, e.g. in [12, 16]. Moreover, for this preliminary test the disturbances are omitted.

Vehicle model with propeller and rudder (VMPR). The second considered model, namely one that is suitable for a hovercraft equipped additionally with a rudder comes from [33]. Equations replacing (4)-(6) are written as follows:

$$\begin{aligned}&\dot{u} = v r -m^{-1}d_u u + m^{-1}b_T T \cos \psi , \end{aligned}$$

(7)

$$\begin{aligned}&\dot{v} = -u r -m^{-1}d_v v + m^{-1}b_T T \sin \psi , \end{aligned}$$

(8)

$$\begin{aligned}&\dot{r} = -J^{-1}d_r r + J^{-1}a b_T T \sin \psi , \end{aligned}$$

(9)

where $b_T$ is input scaling coefficient, T is the thrust force, a is the length of the arm from center of mass to the rudder surface. The symbol m means the mass and J is the inertia. In this model the applied force is $\tau _u= T \cos \psi$ while the applied torque $\tau _r=a \, T \sin \psi$. Several issues must be clarified. Because $m=m_1=m_2$ (for hovercraft) then the average mass is calculated. From the above equations results that also the forces and the torque are different. The equations are related to the design in which both the thrust and the rudder occur. These simplifications may be accepted for preliminary investigation when we want to know the dynamics of the vehicle and show that control is possible at all or which performance of the algorithm can be expected. In this work it is used to compare the control algorithm with controllers intended directly for underactuated marine vehicles.

3 Control schemes for test

There are various algorithms which allow one to control an underatuated underwater vehicle moving in the horizontal plane. Five algorithms were selected for testing from existing controllers. One control scheme is suitable for a hovercraft, another for a ship, and other algorithms for underwater vehicles. Preliminary investigation refers to the situation in which it should be decided to use the algorithm before the final decision concerning selection. For this reason the disturbances are not taken into consideration because we check if the control is useful under the simplified criteria. It is obvious that algorithms dedicated to hovercraft control cannot be used for an underwater vehicle control directly, however in this work an attempt is made to adapt this algorithm to approximate control of the underwater vehicle in the planar motion.

The selected algorithms do not exhaust the range of available control methods and serve only as an example of a comparative test.

3.1 Method and criteria

In this subsection the proposed method and the criteria serving for controller selection are presented.

The method for testing usability of the control schemes is as follows:

• 1. Selection of two underwater vehicles (with a different dynamic) whose model and their nominal parameters are known;

• 2. Preliminary analysis, in which effects of friction forces and any external disturbances are not taken into account (only linear drag coefficients are considered);

• 3. Test of four control algorithms for the VMP model and one for the VMPR model;

• 4. The control algorithm selection is based on seven criteria. The four controllers developed for marine vehicles and one controller developed for hovercraft are tested in simulations;

• 5. The selection of controller parameters and the method of their tuning is based on the procedure described in subsection Selected control schemes;

• 6. Simulation analysis only concerns a circular trajectory tracking task due to its frequent use in simulation studies;

• 7. The comparison among the controllers is carried out on the basis of figures obtained from simulation and the assumed quality indicators.

Criteria for selecting control schemes. The following criteria were assumed for the purpose of the proposed test:

• 1. The equations of motion and used in the control algorithm should be appropriate for one of the vehicle models described in section Underwater vehicle models;

• 2. The control scheme was verified at least on simulation in the original paper;

• 3. The source work must contain full information for simulation verification;

• 4. The control strategy can be a combination of two methods at most (however, it should not require additional methods or knowledge such as neural networks, fuzzy logic or genetic algorithms);

• 5. The method of selecting control coefficients (proposed in the source work) must be simple, e.g. the trial and error method or other intuitive; the use of additional algorithms is not allowed;

• 6. Environmental and inner disturbances, even if they occur in the algorithm, are not taken into account to test only the simplest form of the algorithm;

• 7. Each control algorithm represents another control method.

Comment. In many works it can be seen that no method of selecting the controller’s parameters is given, but only a set of values of the parameters assumed for testing is given, e.g. [11, 14, 29]. Sometimes the trial and error method is proposed [4]. Moreover, only after verifying the effectiveness of the controller without disturbances it can be decided whether to extend the model. Control with disturbances is more difficult and the effectiveness of the algorithm may be lower, therefore they are omitted because the proposed test scheme is to answer the question whether the selected algorithm should be selected for further simulation studies.

3.2 Selected control schemes

The considered, in this subsection, control strategies were chosen taking into account the assumed criteria.

In this work, a comparison among the control schemes proposed for trajectory tracking described in [12, 33, 16, 31], and [4] is shown. After a preliminary study, it turned out that the strategy developed for hovercraft control [33] was promising to achieve this goal. One of the methods is intended to control an underactuated hovercraft, while the others are used originally to control marine vehicles (one is for ships). Here, all algorithms have been applied to the purpose of underactuated underwater vehicle control. The approach in [31] is based on saturated control inputs and, under the assumption on the reference trajectory, the closed-loop system is globally asymptotically stable. The three controllers, i.e. considered in [4, 12, 16] are SMC, TSMC, and combination of SMC with backstepping technique, respectively.

Control scheme 1 (BF - bounded feedback approach) was developed in [31]. The initial dynamics of the vehicle is described by (4)-(6) and the control scheme ensures global asymptotic stability of the tracking error for the system:

$$\begin{aligned} \left[ \begin{array}{c} \dot{e}_x \\ \dot{e}_y \end{array} \right]= & {} -r_{re} A_1 \left[ \begin{array}{c} e_x \\ e_y \end{array}\right] + (D_{\rho }+R_{e_{\psi }} - I d_v) \left[ \begin{array}{c} e_u \\ e_v \end{array} \right] \nonumber \\&+ (\sin {e}_{\psi }\; A_1 + \cos {e}_{\psi }-1)D_{\rho } \left[ \begin{array}{c} u_{re} \\ v_{re} \end{array} \right] , \end{aligned}$$

(10)

$$\begin{aligned} \left[ \begin{array}{c} \dot{e}_u \\ \dot{e}_v \end{array} \right]= & {} -[D + r_{re} A_1]\left[ \begin{array}{c} e_u \\ e_v \end{array} \right] - e_r A_1 \left[ \begin{array}{c} u_{re} \\ v_{re} \end{array} \right] \nonumber \\&+ \left[ \begin{array}{c} 1 \\ 0 \end{array} \right] w_1+ e_r \left[ \begin{array}{c} -e_v \\ e_u \end{array} \right] , \end{aligned}$$

(11)

$$\begin{aligned} \dot{e}_{\psi }= & {} e_r, \;\; \dot{e}_r=\beta (u v - u_{re}v_{re})-e_r+\tilde{w}_2, \end{aligned}$$

(12)

where the control inputs are $w_1 := \tau _{1}-\tau _{1,re}$ and $\tilde{w}_2 := \tau _{2}-\tau _{2,re}$ ($\tau _{1}$ and $\tau _{2}$ mean surge force and yaw moment) whereas u, v, r denote the surge, sway and yaw velocities, respectively. The used matrices are defined as: ${A}_1 = \left[ \begin{array}{cc} 0 &{} -1 \\ 1 &{} 0 \end{array} \right]$, $D_{\rho }=\text{ diag }[\rho , c \rho ]$, $D=\text{ diag }[a/d, b/d]$ are two matrices depending on the mechanical parameters of the system (where $a=d_u/m_1$, $b=d_v/m_2$, $c=m_1/m_2$, and $d=d_r/m_3$). The symbol $\rho$ is a positive constant whereas other symbols are defined in (4)- (6). Moreover, I denotes the identity matrix and $R_{e_{\psi }} = \left[ \begin{array}{cc} \cos e_{\psi } &{} -\sin e_{\psi } \\ \sin e_{\psi } &{} \cos e_{\psi } \end{array} \right]$ is the matrix transforming the error $e_{\psi }$.

The error system (representing the position errors $e_x, e_y, e_{\psi }$ and velocity errors $e_u, e_v, e_r$) is defined in the following form: $e_x = (x-x_{re})\cos {\psi }_{re} + (y-y_{re})\sin {\psi }_{re}$, $e_y = -(x-x_{re})\sin {\psi }_{re} + (y-y_{re})\cos {\psi }_{re}$, $e_u= u-u_{re}$, $e_v=v-v_{re}$ $e_{\psi } =\psi -\psi _{re}$, $e_r=r-r_{re}$ where subscripts re concern the reference signals (the symbols without subscript concern the actual signals).

Under the assumption that there are constraints on the control inputs and velocities is true:

$$\begin{aligned} \left| \tau _{1,re}\right|&\le \bar{\tau }^{re}_{1,max}, \; \left| \tau _{2,re}\right| \le \bar{\tau }^{re}_{2,max}, \; \left| u_{re}\right| \nonumber \le \bar{u}_{max},\\ \left| v_{re}\right|&\le \bar{v}_{max}, \end{aligned}$$

(13)

if $\bar{\tau }^{re}_{1,max}$, $\bar{\tau }^{re}_{2,max}$, $\bar{u}_{max}$, $\bar{v}_{max}$, while $\psi _{re}$ does not converge to any finite limit (as time tends to infinity). Additionally, absolute values of the control inputs are bounded what means that, $\bar{\tau }_{1,max} > \bar{\tau }^{re}_{1,max}$ and $\bar{\tau }_{2,max} > \bar{\tau }^{re}_{2,max}$. Next, the control inputs condition is valid, i.e. C1: $\beta \frac{\tau ^{2}_{1,max}}{a_1 m_1} < \tau _{2,max}$, where $m_1=\text{ min }(a_1/2, b_1)$ ($a_1$ and $b_1$ are some constants). Defining the control variable $w_2 := \beta (u v - u_{re}v_{re})+\tilde{w}_2$ the following controller ensures global asymptotic stability of the error system (if (13) and condition C1 are fulfilled):

$$\begin{aligned}&w_1=-U_1 \sigma \left( \frac{\xi e_u}{U_1} \right) -\rho \sigma \left( M(e_x + \frac{1}{\mu } e_u)\right) , \end{aligned}$$

(14)

$$\begin{aligned}&w_2=-U_2 \sigma \left( \frac{k_1}{U_2} e_{\psi } +\frac{k_2 - 1}{U_2} e_r \right) , \end{aligned}$$

(15)

for an appropriate selection of constants $U_1$, $\rho$, $\xi$, M, $U_2$, $k_1$, $k_2$, if:

$$\begin{aligned}&a_1>U_1+\rho , \;\; U_1> \frac{\left| a_1 - \frac{b_1}{c}\right| }{\text{ min }(a_1, \frac{b_1}{c})}\rho , \;\; U_2> 0, \nonumber \\&M>0, \;\; k_1>k_2-1>0, \;\; a_1+\xi =\mu \rho , \;\; b_1=\mu c \rho .\nonumber \\ \end{aligned}$$

(16)

Moreover, $\sigma (\cdot )$ means the standard saturation function $\sigma (t)=\frac{t}{max(1,\left| t\right| )}$. Performance of the controller was tested by simulation on a ship model.

In order to show that controller given by (14)-(15) ensures the global asymptotic stability of the error system (10)-(12) we can use the methodology described in [31].

S1.:

First the errors $e_{\psi }$, $e_r$ are considered taking large values of $k_1, k_2$ in the control input $w_2$. From (12) and (15) it arises that $\dot{e}_r=-e_r-U_2 \sigma \left( \frac{k_1}{U_2} e_{\psi } +\frac{k_2 - 1}{U_2} e_r \right)$.

S2.:

Second, the first lemma saying that for $U_2 > 0$ and $k_1> k_2-1 > 0$, after sufficiently long time, the saturated control operates in its linear region, exponentially convergence of the errors $e_{\psi }$ and $e_r$ is ensured, is applied. Proof of this lemma is based on the Lyapunov function $V=\frac{1}{2}\alpha e_r^2+ \zeta \left( \frac{k_1}{U_2} e_{\psi } +\frac{k_2 - 1}{U_2} e_r \right)$ (where $\zeta (\iota )=\int ^{\iota }_{0}\sigma (s)ds$). Next, selecting $\alpha =\frac{k_1-k_2+1}{U_2^2}>0$ and setting $z:=\frac{k_1}{U_2} e_{\psi } +\frac{k_2 - 1}{U_2} e_r$ results in $\dot{V}=-\alpha e_r^2-(k_2-1)\sigma ^2(z)$. Since $\dot{V}<0$ for $(e_{\psi }, e_r)\ne (0,0)$ then after a finite time one gets $\left| \frac{k_1}{U_2} e_{\psi } +\frac{k_2 - 1}{U_2} e_r\right| \le 1$. In such case the dynamics described by $\dot{e}_{\psi }= e_r$, $\dot{e}_r=-k_1 e_{\psi }-k_2 e_r$ is linear. Because $k_1, k_2 > 0$ therefore $(e_{\psi }, e_r)$ converges to zero exponentially. From the lemma it follows that under the controller $w_2$ the errors $e_{\psi }$, $e_r$ from (12) converge to zero.

S3.:

The second lemma concerns the errors $e_u$, $e_v$ from equations (10)-(11). It is assumed that the constants $\mu$ and $\xi$ are chosen so that $a_1+\xi =\mu \rho$, $b_1=\mu c \rho$, and additionally $a_1>U_1+\rho$, $U_1 > \frac{\left| a_1 - \frac{b_1}{c}\right| }{\text{ min }(a_1, \frac{b_1}{c})}\rho$. Under these conditions the controller $w_1:=-U_1 \sigma \left( \frac{\xi e_u}{U_1} \right) -\rho \sigma _1 (\cdot )$ (the term $\sigma _1 (\cdot )$ will be determined later) ensures that $e_u$, $e_v$ meet the following inequality:

$$\begin{aligned}&\lim \sup _{t \rightarrow \infty } \Vert (e_u, e_r) \Vert \le \frac{\rho }{\sqrt{m_2 \tilde{a}}}, \tilde{a}= \inf _{t>0} (a_1+ \xi a_{\xi })> 0, \nonumber \\&\quad a_{\xi }=\frac{\sigma (\xi e_u/U_1)}{\xi e_u/U_1}, m_2:=\text{ min }(\tilde{a}/2,b_1). \end{aligned}$$

(17)

In the proof the fact that $\tilde{a}>0$ and then $\xi >0$ (or $\tilde{a}\ge a_1+\xi =\frac{b_1}{c}$) is used. Therefore, one has $e_u\dot{e}_u+e_v\dot{e}_v=-a_1 e_u^2-b_1 e_v^2+e_r(e_u v_{re}-e_v u_{re})+e_u w_1$. Substituting now the controller $w_1$ one obtains $e_u\dot{e}_u+e_v\dot{e}_v \le -a_1 e_u^2-b_1 e_v^2-U_1 e_u \sigma (\xi e_u/U_1)-\rho e_u \sigma (\cdot )+ C_0 |e_r|\sqrt{e_u^2+e_v^2}$ (where $C_0:=\bar{u}_{max}+\bar{u}_{max}$). Since it follows from the lemma considered in S 2 that for a long time $e_r$ tend to zero, therefore (17) follows from the inequality:

$$\begin{aligned} e_u\dot{e}_u+e_v\dot{e}_v \le -m_2 (e_u^2+e_v^2) + \frac{\rho ^2 \sigma _1^2(\cdot )}{\tilde{a}}. \end{aligned}$$

(18)

This lemma shows only that $e_u$, $e_v$ converge to the neighborhood of zero. However, if $\tilde{a}\ge \text{ min }(a_1,\frac{b_1}{c})$ then $\lim \sup _{t \rightarrow \infty } | \frac{\xi e_u}{U_1}| < 1$ what means that the controller exits saturation in a finite time and reaches its linear operating region. In this case $\sigma \big (\frac{\xi e_u}{U_1}\big )=\frac{\xi e_u}{U_1}$, which leads to the equations (instead of (11)):

$$\begin{aligned}&\dot{e}_u=-\mu \rho e_u + r_{re}e_v- \rho \sigma _1(\cdot )+e_r v_{re} - e_r e_v,\\&\dot{e}_v=-\mu c \rho e_v - r_{re}e_u- e_r u_{re} + e_r e_u. \end{aligned}$$

S4:

. The following quantity $W=(W_1,W_2)^T:=(e_x,e_y)^T+(e_u,e_v)^T/\mu$ is defined. According the third lemma W tends to a finite limit $\bar{W}=(0,\bar{W}_2)^T$ if the controller $w_1$ (14) and $\sigma _1(\cdot )=\sigma (M W_1)$ (M means an arbitrary positive constant) are used. Moreover, a function $\mathcal{O}(f(x))$ of order less or equal to f(x) is introduced. In the proof the W dynamics is given in the form:

$$\begin{aligned} \dot{W}= & {} -r_{re} A_1 W + \frac{r_{re}}{\mu }A_1 \left[ \begin{array}{c} e_u \\ e_v \end{array} \right] + \sin {e}_{\psi }\; A_1 D_{\rho } \left[ \begin{array}{c} u_{re} \\ v_{re} \end{array} \right] \nonumber \\&+ D_{\rho } \left[ \begin{array}{c} e_u \\ e_v \end{array} \right] + \mathcal{O}\left( e_{\psi }^2,|e_{\psi }| \left[ \begin{array}{c} e_u \\ e_v \end{array}\right] \right) \nonumber \\&- D_{\rho } \left[ \begin{array}{c} e_u \\ e_v \end{array} \right] - \frac{r_{re}}{\mu }A_1 \left[ \begin{array}{c} e_u \\ e_v \end{array}\right] - \frac{\rho }{\mu } \sigma (M W_1) \left[ \begin{array}{c} 1 \\ 0 \end{array} \right] \nonumber \\&+ \mathcal{O}(|e_r|(1+ \left\| (e_u, e_v) \right\| )). \end{aligned}$$

(19)

Next, the $\lim \sup \left\| W\right\|$ must be found. In order to do that the following expression is determined:

$$\begin{aligned} W^T\dot{W}= & {} \sin {e}_{\psi }\; W^T A_1 D_{\rho } \left[ \begin{array}{c} u_{re} \\ v_{re} \end{array} \right] \\&+ W^T \left[ \mathcal{O}\left( e_{\psi }^2,|e_{\psi }| \left[ \begin{array}{c} e_u \\ e_v \end{array} \right] + \mathcal{O}(|e_r|) \right) \right] \\&- \frac{\rho }{\mu }W_1 \sigma (M W_1)\\= & {} \mathcal{O}(\left\| W\right\| , \left\| e_{\psi }, e_r\right\| )- \frac{\rho }{\mu } W_1 \sigma (M W_1). \nonumber \end{aligned}$$

From these calculations, it follows that $|W^T \dot{W}|+\frac{\rho }{\mu } W_1 \sigma (M W_1)\le \left\| W \right\| \mathcal{O}(\left\| e_{\psi }, e_r \right\| )$. It can be deduced that the time derivative of $\left\| W\right\|$ is integrable over $\mathbb {R}_+$ (positive real numbers space) which means that W has a limit when t tends toward infinity. The right-hand side of the inequality is also integrable over $\mathbb {R}_+$. Hence the same conclusion applies $\frac{\rho }{\mu } W_1 \sigma (M W_1)$. Since W and $\dot{W}$ are bounded, so after applying Barbalat’s lemma, one obtains $W_1 \rightarrow 0$ as $t \rightarrow \infty$. Therefore, also when $t \rightarrow \infty$ then $W_2$ tends to a finite value $\bar{W}_2$.

S5:

. The fourth lemma is: when the lemma of S 3 and S 4 holds, then both $e_u$ and $e_v$ converge to zero asymptotically. Using the lemma from S 3 and the expression $G(e_u,e_v):=(e_u^2+e_v^2)/2$, the Eq. (18) has the form $\dot{G}+2 m_2 G \le (1/\tilde{a})\rho ^2 \sigma _1^2(M W_1)$. As a result, G and $\dot{G}$ are bounded and satisfy the conditions:

$$\begin{aligned} \lim \sup _{t \rightarrow \infty } G \le \frac{\rho ^2}{2 \tilde{a} m_2}, \lim \sup _{t \rightarrow \infty } |\dot{G}| \le 2\frac{\rho ^2}{\tilde{a}}. \end{aligned}$$

However, because $W_1$ is integrable over $\mathbb {R}_+$ and G, and $\dot{G}$ are bounded therefore it follows from Barblat’s lemma that $G \rightarrow 0$ as $t \rightarrow \infty$. Consequently, $e_u$ and $e_v$ converge to zero asymptotically. From the analysis carried out so far it follows that the convergence of errors $e_{\psi }$, $e_r$, $e_u$, $e_v$ to zero is guaranteed. Moreover, from the lemmas given in S 4 and S 5 one can deduce that if $W_1 \rightarrow 0$ and $e_u \rightarrow 0$, then also $e_x$ converges asymptotically to zero.

S6:

. At this stage convergence of the error of the last variable $e_y$ is considered. The last lemma states that if the assumption (13) is satisfied then $\bar{W}=0$ and $e_y$ converges asymptotically to zero. Using (19) the dynamics of W can be written as $\dot{W}=-r_{re} A_1 W + \mathcal{O}(|e_{\psi }|,|e_r|, W_1\sigma (MW_1))$. Now, the new variable, namely $\tilde{W}:=R_{\psi _{re}}W$ (where the matrix $R_{\psi _{re}}$ is analogous to the matrix $R_{e_{\psi }}$) is introduced. The equation of dynamics $\tilde{W}$ is:

$$\begin{aligned}&\dot{\tilde{W}}= \dot{\psi }_{re}A_1 R_{\psi _{re}}W - r_{re}R_{\psi _{re}}A_1 W\nonumber \\&\qquad + R_{\psi _{re}}\mathcal{O}(|e_{\psi }|,|e_r|, W_1\sigma (MW_1)) \nonumber \\&=\mathcal{O}(|e_{\psi }|,|e_r|, W_1\sigma (MW_1)). \end{aligned}$$

(20)

Recall from S 2 that $e_{\psi }$ and $e_r$ converge to zero exponentially. and from S 4 it follows that $W_1 \sigma (M W_1)$ is integrable over $\mathbb {R}_+$. Therefore, $||\dot{\tilde{W}}||$ is also integrable over $\mathbb {R}_+$. This in turn means that $\tilde{W}$ converges to a finite limit $W^L$. Consequently, $-W_2 \sin \psi _{re}$ and $W_2 \cos \psi _{re}$ are going to $W_1^L$ and $W_2^L$, respectively, as t tends to infinity. However, when $\tilde{W}_2 \ne 0$, it can be shown that $\psi _{re}$ converges to the finite limit by checking whether the reference signal $(W_{re})_2=0$ or not. However, with this result a contradiction with assumption (13) arises and so we conclude that W as well as $e_y$ must converge asymptotically to zero. Because use of the controller (14)–(15) leads to $e_{\psi }$, $e_r$, $e_u$, $e_v$, $e_x$, $e_y$ asymptotic convergence to zero then it also ensures the global asymptotic stability of the error system (10)-(12).

Comment. The set of controller parameters can be divided into three groups, namely $a_1, U_1, \rho$ ($a_1$ is chosen arbitrarily), $k_1, k_2$, and $b_1, \beta , U_2, M$. The parameters of the latter group can be selected arbitrarily and independently, however, with the the control inputs condition and (16). The control strategy was originally intended for a ship. However, due to formally the same equations of motion used, it can also be applied to control an underwater vehicle.

Control scheme 2 (SMC and backstepping) was proposed in [4]. The controller was implemented originally for an underactuated underwater vehicle. Because here there is only a preliminary test the disturbances are omitted. The time derivatives of the control signals can be written as follows:

$$\begin{aligned} T_u&=-c_1(\hat{F}_1+\tau _u)-\dot{\hat{F}}_1(S_1)-k_{s1} \text{ sgn }(S_1)\nonumber \\&\quad - w_{s1} S_1-\dot{x}_e(k_1, \dots ) - m_1 u_e(k_1, \dots ) , \end{aligned}$$

(21)

$$\begin{aligned} T_r&=-c_2(\hat{F}_3+\tau _r)-\dot{\hat{F}}_3(S_2)- k_{s2} \text{ sgn }(S_2)\nonumber \\&\quad - w_{s2} S_2 - m_3 r_e(k_3, \dots ) -m_3 \dot{Q}_2(k_2, k_3, \dots ) , \end{aligned}$$

(22)

where $T_u=\dot{\tau }_u$, $T_r=\dot{\tau }_r$, $\dot{\hat{F}}_1(S_1)=u_e + c_1 S_1$, $\dot{\hat{F}}_2=\alpha _{v e}$, $\dot{\hat{F}}_3(S_2)=r_e + c_2 S_2$ are the adaptive laws of the appropriate uncertain terms ${F}_1=m_2 v r -d_u u - m_1 \dot{u}_d$, ${F}_2=-m_1 u r -d_v v$, ${F}_3= (m_1-m_2) u v-d_r r - m_3 \dot{r}_d$ ($\hat{F}_1$, $\hat{F}_2$, $\hat{F}_3$ are approximate values of the uncertain terms). Moreover:

$$\begin{aligned}&S_1=c_1 u_e + m_{1}^{-1}(\hat{F}_1 + \tau _u + x_e), \end{aligned}$$

(23)

$$\begin{aligned}&S_2=c_2 r_e + m_3^{-1} (\hat{F}_3 + \tau _r) + Q_2. \end{aligned}$$

(24)

mean sliding manifolds related to $\tau _u$ and $\tau _r$. Moreover, $u_e, \alpha _{v e}, r_e$ mean error variables. Other symbols have been adopted in accordance with [4].

Comment. Depending on the role and function, the control parameters can be grouped as follows: first group $k_1, k_2, k_3$ (it concerns the position errors and the virtual error), second group $c_1, c_2$ (parameters used in the adaptive laws), and third group $k_{s1}, k_{s2}$, $w_{s1}, w_{s2}$ (parameters for direct adjustment of suitable sliding surfaces). In [4] the parameters were selected by trial and error to ensure good results of tracking an underactuated underwater vehicle in various scenarios and for various trajectories. For this reason, this control algorithm was chosen to perform the circular trajectory tracking task.

Control scheme 3 (SMC) comes from [12] and was tested on a planar model of an underactuated vehicle. The equations of input signals for the vehicle can be given in the following form:

$$\begin{aligned}&\tau _u=m_1 \big (\dot{u}_d -\lambda _1 e_u - k_1 S_1 \nonumber \\&\quad - W_1 \text{ sgn }(S_1) \big )-d_u u - m_2 v r , \end{aligned}$$

(25)

$$\begin{aligned}&\tau _r= b^{-1}\big (-m_2^{-1}(d_v \dot{v}-m_1 \dot{u}r)+ \Gamma - \lambda _3 \dot{e}_v \nonumber \\&\quad - \lambda _2 e_v -k_2 S_2 - W_2 \text{ sgn }(S_2) \big ) \nonumber \\&\quad -d_r r -(m_1 - m_2) u v, \end{aligned}$$

(26)

where $b= m_3^{-1} (- (m_1/m_2) u+u_d)$ and:

$$\begin{aligned}&\Gamma =\Gamma (l_x, l_y, k_x, k_y, \dots ), \end{aligned}$$

(27)

which means that it is a function of many variables. The sliding surfaces are defined as $S_1$ and $S_2$, namely:

$$\begin{aligned} S_1= & {} e_u + \lambda _1 \int ^{t}_{0}e_u(\tau ) d\tau , \;\; \nonumber \\ S_2= & {} \dot{e}_v + \lambda _3 e_v + \lambda _2 \int ^{t}_{0}e_v(\tau ) d\tau . \end{aligned}$$

(28)

Moreover, $e_u=u-u_d$, $e_v=v-v_d$, $x_e=x-x_d$, $y_e=y-y_d$. The desired velocities are given in the form:

$$\begin{aligned} \left[ \begin{array}{c} u_d \\ v_d \end{array} \right] = \left[ \begin{array}{cc} \cos \psi &{} \sin \psi \\ -\sin \psi &{} \cos \psi \end{array} \right] \left[ \begin{array}{c} \dot{x}_d + l_x \tanh \big (-(k_x/l_x) x_e \big ) \\ \dot{y}_d + l_y \tanh \big (-(k_y/l_y) y_e \big ) \end{array} \right] .\nonumber \\ \end{aligned}$$

(29)

Comment. The control parameters can be divided into three groups. First group composed of $l_x$, $l_y$, $k_x$, $k_y$ is used to adjust the position errors $x_e$, $y_e$. The parameters $\lambda _1$, $\lambda _2$, $\lambda _3$ (second group) are included not only in sliding surfaces equations (27) but also in $\tau _u$ (25) and $\tau _r$ (26). The gains of the third group, i.e. $k_1$, $k_2$, $W_1$, $W_2$ are designed to control sliding surfaces directly. The strategy was validated in simulation on an underwater vehicle model for various trajectories. Moreover, in the simulations the same design control gains were applied. In this work it is applied to tracking a different desired trajectory and for vehicles with different dynamics than the originally used.

Control scheme 4 (TSMC), namely the terminal sliding mode controller was described in [16]. This scheme is suitable for control of an underactuated underwater. The equations of input signals are given in the form:

$$\begin{aligned} \tau _u= & {} m_1 \big (\dot{u}_d - \beta _1 (q_1/p_1) e_u (\tilde{e}_u)^{\frac{q_1}{p_1}-1} - W_1 \text{ sgn }(S_1) \big )\nonumber \\&-d_u u - m_2 v r , \end{aligned}$$

(30)

$$\begin{aligned} \tau _r= & {} {m_3} \big (-(m_1/m_2)u+u_d \big )^{-1} \big (m_2^{-1} (-d_r \dot{v}+ m_1 \dot{u} r) \nonumber \\&+ \Gamma - \beta _2 (q_2/p_2) \dot{e}_v ({e}_v)^{\frac{q_2}{p_2}-1} - W_2 \text{ sgn }(S_2) \big )\nonumber \\&-d_r r -(m_1- m_2) u v \end{aligned}$$

(31)

where $\Gamma$ is calculated from (27), $u_d$, $v_d$ are obtained from (29). The sliding surfaces are defined as follows:

$$\begin{aligned}&S_1=e_u + \beta _1 (\tilde{e}_u)^{q_1/p_1}, \;\; S_2=\dot{e}_v + \beta _2 (e_v)^{q_2/p_2}, \end{aligned}$$

(32)

where the position errors are $x_e=x-x_d$, $y_e=y-y_d$, the velocity errors are defined as $e_u=u-u_d$, $e_v=v-v_d$, while $\tilde{e}_u$ means the velocity error integral. The reference [16] contains remark to replace expression $\text{ sgn }(S)$ by formula $\text{ sat }(S)$ in order to avoid chattering.

Comment. Also in this control scheme, three groups of parameters can be distinguished. The first group consists of $l_x$, $l_y$, $k_x$, $k_y$ which play the same role as in Control scheme 3. The second group of parameters, i.e. $\beta _1$, $\beta _2$, $q_1/p_1$, $q_2/p_2$ is used to tuning sliding surfaces $S_1$ and $S_2$. The parameters of the third group, composed of $W_1$, $W_2$ are designed for direct tuning of $\text{ sgn }(S_1)$ and $\text{ sgn }(S_2)$. Despite of that this control algorithm seems to be similar to Control scheme 4 the sliding surfaces are determined differently. The controller was tested via simulation using model of an underwater vehicle. In [16] simulation results of the control method were performed using linear and circular desired trajectories. The underwater vehicle in source work was different than the one investigated here. Because of satisfactory numerical results obtained in the original paper the approach seems to be promising.

Control scheme 5 (Lyapunov theory based algorithm - LTBA) is taken from [33]. The control objective was to track a desired trajectory $\mathbf {p}_d$ having a fixed point defined in the body frame $\varvec{\delta } \in R^2$. This point may be the center of mass but not necessarily. Omitting disturbances, as assumed earlier, the input signals in the Eqs. (7)–(9) have the following form:

$$\begin{aligned}&\left[ \begin{array}{c} T \cos \psi \\ T \sin \psi \end{array} \right] =-\mathbf {B}^{-1} \bigg ( \mathbf {R}^{T}(k_1 \mathbf {z}_1+k_2 \mathbf {z}_2) + \mathbf {F}_0 \bigg ), \end{aligned}$$

(33)

where:

$$\begin{aligned}&\mathbf {z}_1=\mathbf {p}-\mathbf {p}_d+ \mathbf {R}\varvec{\delta }, \;\;\; \mathbf {z}_2=\dot{\mathbf {z}}_1=\mathbf {R}\mathbf {v}-\dot{\mathbf {p}}_d+ \mathbf {R}\mathbf {S}\varvec{\delta }r, \end{aligned}$$

(34)

and $\mathbf {B} = b_T \; \text{ diag } [ m^{-1}, m^{-1}-J^{-1}\delta _x a ]$, $\mathbf {R} = \left[ \begin{array}{cc} \cos \psi &{} -\sin \psi \\ \sin \psi &{} \cos \psi \end{array} \right]$, $\mathbf {S} = \left[ \begin{array}{cc} 0 &{} -1 \\ 1 &{} 0 \end{array} \right] , \; \varvec{\delta } = \left[ \begin{array}{c} \delta _x \\ 0 \end{array} \right]$ (if $a\delta _x \ne m^{-1} J$). The vector $\mathbf {F}_0$ depends on $m, d_u, u , d_v, v, d_r, r, \mathbf {R}, \ddot{\mathbf {p}}_d, \delta _x, J$. Moreover, $\mathbf {v}=[u \;\; v]^T$ means the linear velocity vector.

Comment. The control gains denoted by $k_1, k_2$ are the first group of control parameters. The second group is composed of $\delta _x$ and a. The parameter $\delta _x$ changes the values of position errors for a fixed motion phase while the parameter a affects the duration of the transitional movement phase. The control strategy was verified in [33] on a hovercraft both in simulation and in real experiment. The control algorithm is designed originally for a hovercraft equipped with a rudder. As some underwater vehicles also have a rudder (in addition to the propeller) this control strategy was also selected for the test.

Control parameters selection. A control scheme that is easy to implement should be based on a simple parameter selection method. Such an idea can be found in many works, where no method for the selection of these parameters is given at all, which suggests that this is a task that does not require additional numerical effort. Such an approach was presented, e.g., in [5, 10, 11, 13,14,15, 18, 29, 32]. However, the trial and error method is mentioned in [4].

In this work a heuristic method of searching for controller parameters was used, namely tuning based on grouping those controller parameters that serve the same purpose or function. At the beginning, there is a division into groups of parameters taking into account the tasks mentioned above. The search starts with small parameter values. The evaluation of their influence on the operation of the controller is made on the basis of observation of the simulation results. Then the parameter values are changed separately within one group to recognize the effects of these changes. On the basis of visualization of the effects of parameters from the same group (other parameters may have unit values and if such values are too high, then they are reduced so that they are close to zero) further procedure is decided. In case when the values set for several parameters lead to a goal, at least partially, e.g. convergence of position errors has been achieved, but the results are still unsatisfactory, then the influence of other parameters on the controller’s work can be examined. If the results are acceptable, parameters from other groups are only tuned. In case of improving the quality of control (visible on figures), it is possible to tune the values from the examined group of parameters or those that were previously selected. If the results are promising, the influence of the next group of parameters on the correctness of the trajectory tracking task is checked. When the results improve the performance of the controller, we change the values of the next group of parameters and check if position errors have been corrected. The procedure is repeated until the parameter values are found that ensure acceptable results obtained with the tested controller. This approach was applied to tune the parameters of the selected control algorithms.

4 Simulation results

4.1 Performance test assumptions

The tested vehicles and their parameters are quite different than the originally tested in the literature control algorithms.

The numerical simulations were carried out to show effectiveness of the controllers. The aim of the simulation test is to show the performance of the selected algorithms for the Kaxan ROV which parameters are taken from [34] and the Tokyo University of Marine Science and Technology (TUMST) AUV described in [35, 36]. Both vehicles have different shape and dynamics which results from their set of parameters. In the case of Control scheme 5, a simulation test is performed to investigate the applicability of this algorithm to vehicles with Kaxan and TUMST dynamics (e.g., it may be useful in the design stage of a modified vehicle).

Conditions of the investigation done in Matlab/Simulink were as follows: the forces and torques values were limited due to the underwater design, i.e. $|\tau _u| \le 100$ N, (or $|T| \le 100$ N) $\tau _r \le 100$ Nm, time of motion $t=60$ s (only for Control scheme 1 in which $t=350$ s and $t=600$ s were assumed due to the long time to reach an acceptable position error value) , $\Delta t= 0.01$ s using the method ODE 3 Bogacki-Shampine.

For tracking it is assumed the desired trajectory position profile described as:

$$\begin{aligned}&p_{d} = \left[ \begin{array}{c} 5 \sin (0.12\, t) \\ 5 \cos (0.12\, t) \end{array} \right] . \end{aligned}$$

(35)

All algorithms used for control of the underwater vehicle were tested on a hovercraft [33] (in [37]) and original marine vehicle described in the cited references, i.e. [4, 31] (in [38]), [12] (in [39]), [16] (in [40]).

In order to ensure the same working conditions, the following initial points: $p_0=[0.2\;\; -0.2\;\; 0]^T$ (for Control scheme 1), $p_0=[-0.2\;\; 5.2\;\; 0]^T$ (for Control scheme 2, 3, and 4), $p_0=[-0.2\;\; 5.2]^T$ (for Control scheme 5 in which the angular position is not taken into consideration) were assumed.

The software used for all method control algorithms tested here was written in MATLAB/Simulink environment and tested on the original data given in the source literature.

4.2 Comparison of control schemes

In this subsection the algorithms given earlier were used in simulations.

4.2.1 Kaxan ROV

The first vehicle, namely Kaxan ROV set of parameters is as follows [34]: $m=98.5$ kg, $J=2.32$ kg m$^2$, $X_{\dot{u}}=-29$ kg, $Y_{\dot{v}}=-30$ kg, $N_{\dot{r}}=-3.3$ kg m$^2$. Moreover, because of the form of control formulas, the linear drag coefficients are assumed as $d_u=72$ kg/s, $d_v=77$ kg/s, $d_r=30$ kgm/s (for [31, 33]) and $d_u=-72$ kg/s, $d_v=-77$ kg/s, $d_r=-30$ kgm$^2$/s (for [12, 16]).

Firstly, Control scheme 1 presented in [31] using MATLAB/Simulink developed in [38] was tested. The assumed applied force was ${\tau }^{re}_{1, max}=0.25$ N and the applied torque ${\tau }^{re}_{2, max}=0.02$ Nm. The system parameters were calculated for Kaxan ROV [34], while the parameters of the controller were selected after many attempts as: $a_1=4.2$, $b_1=4.5$, $k_1=10.0$, $k_2=10.0$, $U_1=a_1/2$, $U_2=0.2$, $\rho =a_1/12$, $M=0.25$, and $\beta =0.13$. In this method the desired trajectory must be scaled changing the regulator’s parameters based on the trial and error method. This is an additional difficulty.

As it is shown in Fig. 2a the tracking task is realized correctly but after a long time (about 300 s as it is seen in Fig. 2b). However, it can be expected that with other controller parameters this time could be reduced. The velocities given in Fig. 2c, and the applied force and torque in Fig. 2d have small values.

Fig. 2

Simulation results for Kaxan with Control scheme 1 and circular trajectory: a desired and realized trajectory; b position errors; c velocities; d applied force and torque

Fig. 3

Simulation results for Kaxan with Control scheme 2 and circular trajectory: a desired and realized trajectory; b position errors; c velocities; d) applied force and torque

The second test was performed for Control scheme 2 [4] using software made in [38]. Unfortunately, after many attempts, it turned out to be impossible to obtain such a set of control coefficients that would ensure the correct realization of the task of tracking the desired circular trajectory. Results with quality similar to the results in work [4] could not be obtained. Satisfactory results could be expected because the trial and error method was suggested in the original paper. After long search, the following set of parameters was assumed: $k_1=1.19$, $k_2=1.19$, $k_3=0.81$, $c_1=1.0$, $c_2=1.0$, $k_{s1}=0.8$, $k_{s2}=0.8$, $w_{s1}=2.5$, $w_{s2}=2.5$. Moreover, the controller’s work depended very much on small changes in parameters. The simulation results are presented in Figure 3.

From Fig. 3a it is seen that the desired trajectory is not tracked with acceptable accuracy. This observation is confirmed in Fig. 3b because large trajectory tracking errors $\Delta p_x$ and $\Delta p_y$ occur. In Fig. 3c noticeable velocities fluctuation when the vehicle moves. Oscillating effect is also visible for the force $\tau _u$ and the torque $\tau _r$ in spite of that they have limited values.

Fig. 4

Simulation results for Kaxan with Control scheme 3 and circular trajectory: a desired and realized trajectory; b position errors; c velocities; d applied force and torque

Fig. 5

Simulation results for Kaxan with Control scheme 4 and circular trajectory: a desired and realized trajectory; b position errors; c velocities; d applied force and torque

As the next algorithm Control scheme 3 [12] using software from [39] was investigated. For this control scheme it also turned out to be impossible to achieve acceptable performance using the proposed parameter tuning procedure. Very significant sensitivity of results to changes in controller parameters, instability of the control algorithm and large errors in tracking the desired trajectory were noticed. This is rather strange because the results shown in work [12] were satisfactory for a circular trajectory although for another vehicle (the algorithm was previously tested in [39] for the vehicle and conditions given in the original work [12]). Maybe another method of searching for coefficients would give better results (which, however, was excluded in the assumptions of the initial test). After many unsuccessful attempts, it was decided to show simulation results for the following set of coefficients: $l_x=16$, $l_y=16$, $k_x=1.5$, $k_y=1.5$, $\lambda _1=5$, $\lambda _2=6$, $\lambda _3=8$, $k_1=0.102$, $k_2=0.102$, $W_1=0.5$, and $W_2=1.8$.

As it can be observed in Fig. 4a the trajectory tracking task is not realized at all. This observation is confirmed in Fig. 4b where we see that the position errors do not tend to zero. Also the velocities (given in Fig. 4c) oscillate and have great values if the vehicle moves. The applied force and torque (Fig. 4d) have limited values but their fluctuations are unacceptable from the point of view of effective trajectory tracking.

Fig. 6

Simulation results for Kaxan with Control scheme 5 and circular trajectory: a desired and realized trajectory; b position errors; c velocities; d applied forces

The fourth Control scheme 4 proposed in [16] was examined using software prepared in [40]. It turned out that for this controller the selection of control parameters using the proposed method is easier, which means that the time after which satisfactory results were obtained was shorter and required fewer attempts than the previous algorithm. After many attempts, the following coefficients were assumed: $l_x=3$, $l_y=3$, $k_x=0.2$, $k_y=0.2$, $\beta _1=1$, $\beta _2=1$, $q_1/p_1=1/2$, $q_2/p_2=5/7$, $W_1=4.0$, and $W_2=4.0$. Moreover, the initial values of error integrals were taken such that $\tilde{e}_u(0)=0.0001$ and $\tilde{e}_v(0)=0$.

From Fig. 5a it can be seen that the trajectory tracking task is realized correctly. The position errors are close to zero after about 25 s (Fig. 5b). If the vehicle starts then both position errors increase but next they tend to zero. Such an effect results from the dynamics of the vehicle. The velocities achieve constant values quickly, namely after about several second as it is shown in Fig. 5c. But the angular velocity r increase significantly in the first phase of motion but later decreases highly. As it is seen from Fig. 5d the applied force and torque are approaching constant values quickly.

The results for the Control scheme 5 [33] were obtained using software from [37]. In the test identification of dynamic parameters and disturbances arising from friction are omitted. This simplification enables comparison of results under the same work conditions. The set of parameters was as follows: $a=0.7$ m, $\delta _x=0.001$ m, $b_T=0.5$ and the controller gains as $k_1=1.0$, $k_2=1.0$. Note that they are very close to the gains used originally in [33] for quite different vehicle, i.e. hovercraft and the desired trajectory ($k_1=k_2=2$). The parameters estimator was off.

As it arises from Fig. 6a the tracking trajectory task is realized correctly. After about 15 seconds, both position errors are close to zero (Fig. 6b) (their end values depend on the parameter $\delta _x$ which is assumed arbitrarily). The velocities, as it is shown in Fig. 6c, have only at the beginning high values. Finally, from Fig. 6d it can be observed that in the first phase of motion the forces have the greatest values which next decrease significantly (the torque depend on $T \sin \psi$. The applied forces were limited to 100 N.

4.2.2 TUMST AUV

The second vehicle’s model, namely TUMST AUV (Tokyo University of Marine Science and Technology AUV) was described in [35, 36]. Its set of parameters is as follows: $m=390$ kg, $J=305.67$ kg m$^2$, $X_{\dot{u}}=-49.12$ kg, $Y_{\dot{v}}=-311.52$ kg, $N_{\dot{r}}=-87.63$ kg m$^2$. Moreover, because of the form of control formulas, the linear drag coefficients are assumed as $d_u=20$ kg/s, $d_v=200$ kg/s, $d_r=200$ kgm/s (for [31, 33]) and $d_u=-20$ kg/s, $d_v=-200$ kg/s, $d_r=-200$ kgm$^2$/s (for [12, 16]).

Fig. 7

Simulation results for TUMST AUV with Control scheme 1 and circular trajectory: a position errors; b velocities

The second test was performed for the Control Scheme 1 provided in [31] using software developed in [38]. The assumed applied force was ${\tau }^{re}_{1, max}=0.25$ N and the applied torque ${\tau }^{re}_{2, max}=0.02$ Nm. The system parameters were calculated for Kaxan ROV [34], while the parameters of the controller were selected after many attempts as: $a_1=3.7$, $b_1=2.235$, $k_1=10.0$, $k_2=10.0$, $U_1=a_1/2$, $U_2=0.2$, $\rho =a_1/90$, $M=0.3$, and $\beta =0.13$. In this method the desired trajectory must be scaled changing the regulator’s parameters based on the trial and error method. This is an additional difficulty.

The tracking task is realized correctly similar to Fig. 2a but after a long time (about 500 s as it is seen in Fig. 7a). However, it can be expected that with other controller parameters this time could be reduced. The velocities given in Fig. 7b, whereas the applied force and torque are close to those shown in Fig. 2d.

Fig. 8

Simulation results for TUMST AUV with Control scheme 2 and circular trajectory: a) desired and realized trajectory; b) position errors; c) velocities; d) applied force and torque

The third test was performed for Control scheme 2 [4] using software made in work [38]. Unfortunately, after many attempts, it turned out to be impossible to obtain such a set of control coefficients that would ensure the correct realization of the task of tracking the desired circular trajectory. Results with quality similar to the results in work [4] could not be obtained (in those reference the trial and error method was suggested). After long search, the following set of parameters was assumed: $k_1=1.6$, $k_2=1.09$, $k_3=0.1$, $c_1=0.8$, $c_2=1.3$, $k_{s1}=0.5$, $k_{s2}=0.5$, $w_{s1}=1.0$, $w_{s2}=1.0$. From Figure 8a it is seen that the desired trajectory is not tracked with acceptable accuracy. This observation is confirmed in Fig. 8b because large trajectory tracking errors $\Delta p_x$ and $\Delta p_y$ occur. In Fig. 8c noticeable velocities fluctuation when the vehicle moves. Oscillating effect is also visible for the force $\tau _u$ and the torque $\tau _r$ in spite of that they have limited values.

Fig. 9

Simulation results for TUMST AUV with Control scheme 4 and circular trajectory: a position errors; b velocities; c applied force and torque

As the next algorithm Control scheme 3 [12] using software from [39] was investigated. For this control scheme it also turned out to be impossible to achieve satisfactory performance using the selection of coefficients using the proposed procedure. Very significant sensitivity of results to changes in controller parameters, instability of the control algorithm and large errors in tracking the desired trajectory were noticed. This is rather strange because the results shown in work [12] were satisfactory for a circular trajectory although for another vehicle (the algorithm was previously tested in [39] for the vehicle and conditions given in the original work [12]). Maybe another method of searching for coefficients would give better results (which, however, was excluded in the assumptions of the initial test). After many unsuccessful attempts, it was decided to show simulation results for the following set of coefficients: $l_x=11$, $l_y=11$, $k_x=10$, $k_y=10$, $\lambda _1=2$, $\lambda _2=7$, $\lambda _3=8$, $k_1=0.1$, $k_2=0.1$, $W_1=0.5$, and $W_2=1.8$. The results obtained in this case are close to those shown in Fig. 4 and have been omitted.

For Control scheme 4 the coefficients serving for TUMST AUV control and working conditions were the same as for Kaxan ROV. The trajectory tracking task is realized correctly as in Case 1 (Fig. 5a). The position errors are close to zero after about 25 s (Fig. 9a). If the vehicle starts then both position errors increase but next they tend to zero. It results from the fact that the initial linear position and angular position have nonzero values. The velocities achieve constant values quickly, namely after about several second as it is shown in Fig. 9b. But the angular velocity r increase significantly in the first phase of motion but later decreases highly. As it is seen from Fig. 9c the applied force and torque are approaching constant values quickly.

In the next test Control scheme 5 was investigated. Conditions of the investigation done in Matlab/Simulink were the same as previously for Kaxan ROV. However, the set of parameters was: $a=3$ m, $\delta _x=0.001$ m, $b_T=0.5$ and the controller gains as $k_1=0.5$, $k_2=0.5$. The parameters estimator was off.

Fig. 10

Simulation results for TUMST AUV with Control scheme 5 and circular trajectory: a) position errors; b) velocities; c) applied forces

The tracking trajectory task is realized correctly as in Figure 6a. After about 30 seconds, both position errors are close to zero as seen in Figure 10a ($\delta _x$ is assumed arbitrarily and the position error depends on the parameter). The velocities, as it is shown in Figure 10b, have only at the beginning high values. Finally, from Figure 10c it can be observed that if the first phase of motion the forces have the greatest values which next decrease significantly (the torque depend on $T \sin \psi$). We also conclude that the applied force may by limited to 100 N.

4.2.3 Comparison based on simulations and indexes

Analysis of simulation results. For Control scheme 1 the results were satisfactory but the time necessary to the task realization was very long (the source work shows that this control strategy is suitable for ships). From a practical point of view this performance is rather unacceptable for underwater vehicles. Control scheme 2 and Control scheme 3 completely failed in the test. It is possible that using additional methods of searching for control parameters would be better, because it goes beyond the assumptions of the initial test considered in this paper. Their performance do not qualify them for the implementation of the task given under the assumptions made. The proposed method of parameter selection proved to be insufficient in these algorithms. However, it should be noted that in preliminary testing additional methods are not allowed and furthermore, as mentioned when describing the heuristic method, in many papers such methods are not mentioned and yet the algorithms are successful. It turned out that Control scheme 4 based on terminal sliding mode approach is effective for the trajectory tracking of the underactuated underwater vehicle under the considered conditions. It worked correctly even the parameters were the same for Kaxan ROV and TUMST AUV.

The Control scheme 5 originally designed to track the underactuated hovercraft trajectory provided acceptable performance also for the underwater vehicle Kaxan. Based on simulation results, possibility of tracking the circular trajectory was confirmed for the underwater vehicles Kaxan and TUMST AUV (values of position errors as well as the values of velocities were acceptable). The applied forces necessary to drive Kaxan vehicle were acceptable. However, for the TUMST AUV, for too long the applied force values have been large and varying over time, which can lead to rudder damage or significant rudder loading. This situation is unacceptable under real conditions. Although this controller gives satisfactory results, its use for underwater vehicles is limited due to the use of the rudder (usually the drive comes from engines).

It can be concluded from the research that if we want to apply known control algorithms, we should first examine them due to the selection of regulator gains because in some algorithms such selection is non-trivial and requires the use of additional methods, e.g. optimization, genetic algorithms. However, in the latter case, the application of the control strategy is more difficult and causes additional complications.

Application of formal criteria In order to compare the algorithms in terms of ensuring the convergence of tracking errors, the mean values and standard deviations were calculated for each controller, for each trajectory and for both vehicles. The results are shown in Table 1.

Table 1 Means (m) and standard deviations (std) of tracking errors for control schemes (Cs)

It turned out that the lowest mean and std values were obtained for Cs 1 (BF) for both vehicles tested. Unfortunately, a serious disadvantage in this case is the very long time of stabilization of position errors, which in the case of underwater vehicles is usually not acceptable. Satisfactory mean and std values for both vehicles were also obtained for Cs 4 (TSMC) and Cs 5 (LTBA) (except for std value for Cs 5, which is large). The mean and std values for Cs 2 (SMC and backstepping) and Cs 3 (SMC) are too large, which indicates a defective operation of these control algorithms (a low mean value for Cs 2 and Kaxan vehicle is misleading because the algorithm is not working properly as i shown in Fig. 3).

Table 2 Mean of norm of input signal effort for control schemes (Cs)

Mean values of norm of input signals effort was for each control scheme was given in Table 2. The table shows that the smallest values of forces and torques to perform a tracking task are necessary for Cs 1 (BF) which is consistent with the assumptions of this control strategy. Small values according to this criterion were also obtained for Cs 4 (TSMC). Acceptable values of the criterion were also obtained for Cs 5 (LTBA) and Cs 2 (SMC and backstepping). However, in the latter case, as shown by simulation studies, the task of trajectory tracking is not realized. The values for Cs 3 (SMC) are practically too high.

5 Test summary and conclusions

In this work, several selected trajectory tracking control algorithms, known from the literature, for underactuated underwater vehicles in horizontal motion were investigated. It turned out that not all control schemes designed to track a desired trajectory gave satisfactory results with the assumptions made, which may be important from a practical point of view. The simulation results obtained for two different 3 DOF underactuated underwater vehicles moving in the horizontal plane have shown the usefulness of each examined algorithm. Tests have also shown that some trajectory tracking methods for underwater vehicles may not be effective when used in a vehicle other than in the reference literature. It should be noted that the simulation tests carried out have a limited range, namely five selected controllers were examined, only the circular trajectory was tracked, and only two vehicles, namely Kaxan ROV and TUMST AUV were considered. Nevertheless, the assumptions of the proposed procedure can be used for further research on adaptation of the control strategy for other underwater vehicles.

The results according to the Cs 1 (BF) strategy turned out to be the best (both the results obtained from the graphs and the formal criteria adopted). This method was also effective in changing the initial condition. However, the biggest disadvantage of this approach is the very long regulation time which makes this algorithm impractical for underwater vehicles. The strategies Cs 2 (SMC and backstepping) and Cs 3 (SMC) turned out to be useless because the task of following the desired trajectory was not performed correctly. This was partially confirmed by formal criteria. Therefore, it can be concluded that the choice of control algorithm for simulation studies may not be easy at all. Of course, in the future, it is possible to propose an additional method of optimizing control parameters, but it must also be remembered that more complicated methods may be much more difficult when carrying out the experiment. At this stage of testing these algorithms are not acceptable for use. The results obtained for Cs 4 (TSMC) are satisfactory and therefore this algorithm is useful for the designated tracking task and for further research. This approach turned out also effective in changing the initial condition. Among the selected algorithms only TSMC proved to be effective, which guaranteed satisfactory performance for both vehicles. The task of trajectory tracking was also performed using Cs 5 (LTBA), however, the results for TUMST AUV are questionable due to the long time of setting the input signals (forces). This may mean that the control algorithm is only suitable for some underwater vehicles. Another limitation is the need to use the rudder.

The proposed approach may be used in the first phase of simulation studies for comparison of various control strategies when it is necessary to decide whether to apply a control strategy and to use a more accurate analysis. The value of the proposed comparative test is to provide information that is helpful in the initial testing of various algorithms. In the future the other control schemes should be tested in order to answer which algorithms lead to acceptable control results.