Energy-saving trajectory planning by using Fourier sine series and tracking control for a mechatronic elevator system

Abstract

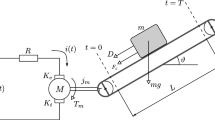
In this paper, Lagrangian method is proposed to formulate dynamic model for a mechatronic elevator system, which includes mechanical and electrical parts. Lagrange equations, i.e. the torque balance equation and voltage balance equation, are derived from the kinetic energy, potential energy and virtual work of the mechatronic system. From the dynamic equations, the energy balance equation is obtained including electromagnetic energy, electrical dissipation energy, mechanical kinetic energy, mechanical dissipation energy, and the mechanical potential energy. The minimum-energy trajectory by using Fourier sine series (FSS) and power series are found by real-coded genetic algorithm. From simulation results, it is found that FSS with less order can find the minimum input energy more quickly than the power series. The four-degree (4-D) FSS trajectory is given as a reference one for the adaptive tracking control. It is found that the proposed adaptive controller has good tracking performance for the 4-D FSS angular displacement and velocity.

Appendices

Appendix A

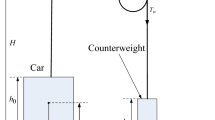
In this appendix, we derive the potential energy of the mechatronic elevator system. The cable height of the elevator system is measured from the position of mass center of the cable to the ground.

The initial height and length of the cable for the car are

$$ l_{c} = \left( {x_{c} + \frac{{h_{0} }}{{2}}{ + }\frac{{l_{1} }}{2}} \right),\quad l_{1} = H - x_{c} - \frac{{h_{0} }}{2}{,}\;{\text{and}}\;\int_{0}^{s} {dS} = \int_{0}^{\theta } {Rd\theta } . $$

(A1a-c)

The differential potential energy $U_{c}$ of the car is

$$ dU_{c} = \rho g\left( {l_{1} - dS} \right)\left( {l_{c} + \frac{dS}{2}} \right) - \rho gl_{1} l_{c} = \rho g\left[ {l_{1} \frac{dS}{2} - l_{c} dS - \frac{{\left( {dS} \right)^{2} }}{2}} \right]. $$

(A2a)

Integrating Eq. (A2a), one can find that

$$ U_{c} = \rho g\left( {\frac{{l_{1} }}{2} - l_{c} } \right)R\theta . $$

(A2b)

Substituting $l_{c}$ in Eq. (A1a) into Eq. (A1b), we have

$$ U_{c} = \rho g\left[ {\left( {\frac{{l_{1} }}{2} - \left( {\frac{{l_{1} }}{2} + x_{c} + \frac{{h_{0} }}{{2}}} \right)} \right)R\theta } \right] = \rho gR\theta \left( { - x_{c} - \frac{{h_{0} }}{2}} \right). $$

(A3)

The initial height and length of the cable for the counterweight are

$$ l_{w} = \left( {x_{w} + \frac{{h_{2} }}{2}{ + }\frac{{l_{2} }}{2}} \right),\quad {\text{and}}\quad l_{2} = H - \frac{{h_{2} }}{2} - x_{w} - h_{1} . $$

(A4a,b)

The differential potential energy $U_{w}$ of the counterweight can be found

$$ dU_{w} = \rho \left( {l_{2} + dS} \right)g\left( {l_{w} - \frac{dS}{2}} \right) - \rho l_{2} gl_{w} = \rho g\left[ { - l_{2} \frac{dS}{2} + l_{w} dS - \frac{{\left( {dS} \right)^{2} }}{2}} \right]. $$

(A5a)

Integrating Eq. (A5a), one can find that

$$ U_{w} = \rho g\left[ {\left( {l_{w} - \frac{{l_{2} }}{2}} \right)R\theta } \right]. $$

(A5b)

Substituting $l_{w}$ in Eq. (A4a) into Eq. (A5b), one can obtain

$$ U_{w} = \rho g\left[ {\left( {\frac{{l_{2} }}{2} + x_{w} + \frac{{h_{2} }}{2}} \right) - \left( {\frac{{l_{2} }}{2}} \right)R\theta } \right] = \rho gR\theta \left( {x_{w} { + }\frac{{h_{2} }}{2}} \right). $$

(A6)

Finally, the total potential energy $U_{b}$ of the cable can be obtained as follows

$$ U_{b} = U_{c} { + }U_{w} = \rho gR\theta \left[ {\left( {x_{w} { + }\frac{{h_{2} }}{2}} \right) - \left( {x_{c} { + }\frac{{h_{0} }}{2}} \right)} \right], $$

(A7)

where $U_{b}$ is the total potential energy of cable.

Appendix B

The general Fourier series with sine–cosine form is shown as follows:

$$ \theta (t) = \sum\limits_{n = 0}^{\infty } {\left( {a_{n} \cos \frac{n\pi t}{{2}} + b_{n} \sin \frac{n\pi t}{{2}}} \right)} , $$

(B1)

where $a_{n}$ and $b_{n}$ are Fourier coefficients, and $n = 0,1,2,\ldots ,\infty .$

The trajectory of angular displacement $\, \theta (t)$, angular velocity $\omega (t)$ and angular acceleration $\alpha (t)$ by using Fourier series with $n = 2$ are described as follows:

$$ \theta (t) = a_{0} + a_{1} \cos \frac{\pi t}{{2}} + b_{1} \sin \frac{\pi t}{{2}} + a_{2} \cos \pi t + b_{2} \sin \pi t, $$

(B2a)

$$ \omega (t) = - a_{1} \frac{\pi }{{2}}\sin \frac{\pi t}{{2}} + b_{1} \frac{\pi }{{2}}\cos \frac{\pi t}{{2}} - a_{2} \pi \sin \pi t + b_{2} \pi \cos \pi t, $$

(B2b)

$$ \alpha (t) = - a_{1} \frac{{\pi^{{2}} }}{{4}}\cos \frac{\pi }{{2}}t - b_{1} \frac{{\pi^{{2}} }}{{4}}\sin \frac{\pi t}{{2}} - a_{2} \pi^{2} \cos \pi^{2} t - b_{2} \pi^{2} \sin \pi t, $$

(B2c)

where $a_{0} ,$ $a_{1} ,$ $a_{2} ,$ $b_{1} ,$ and $b_{2}$ are the unknown coefficients to be determined by initial- and final-time conditions. When the initial- and final-time conditions are $\theta (0) = 0,$ $\theta (1) = 1,$ $\omega (0) = 0,$ $\omega (1) = 0,$ $\alpha (0) = 0,$ and $\alpha (1) = 0,$ the coefficient equations can be obtained as follows:

$$ \begin{aligned} & \theta (0) = a_{0} + a_{1} + a_{2} = 0,\quad \theta (1) = a_{0} - a_{2} + b_{1} = 1,\quad \omega (0) = b_{1} - 2b_{2} = 0, \\ & \omega (1) = a_{1} + 2b_{2} = 0,\quad \alpha (0) = a_{1} + 4a_{2} = 0,\quad {\text{and}}\;\alpha (1) = 4a_{2} - b_{1} = 0. \\ \end{aligned} $$

Because there are six initial- and final-time conditions, and only five unknown coefficients ($a_{0} ,$ $a_{1} ,$ $a_{2} ,$ $b_{1} ,$ and $\, b_{2}$), therefore, one can not exactly solve the five unknown coefficients by using Fourier series with sine–cosine form.

Moreover, Fourier series with cosine form is shown as follows:

$$ \theta (t) = \sum\limits_{n = 0}^{\infty } {a_{n} \cos \frac{n\pi t}{{2}}} , $$

(B3)

where $a_{n}$ is Fourier coefficients with $n = 0,1,2\ldots ,\infty .$

The trajectory of angular displacement $\, \theta (t)$, angular velocity $\omega (t)$ and angular acceleration $\alpha (t)$ by using Fourier series with $n = 5$ are described as follows:

$$ \theta (t) = a_{0} + a_{1} \cos \frac{\pi t}{{2}} + a_{2} \cos \pi t + a_{3} \cos \frac{{{3}\pi t}}{{2}} + a_{4} \cos {2}\pi t + a_{5} \cos \frac{{{5}\pi t}}{{2}}, $$

(B4a)

$$ \omega (t) = - a_{1} \frac{\pi }{{2}}\sin \frac{\pi t}{{2}} - a_{2} \pi \sin \pi t - a_{3} \frac{{{3}\pi }}{{2}}\sin \frac{{{3}\pi t}}{{2}} - a_{4} {2}\pi \sin {2}\pi t - a_{5} \frac{{{5}\pi }}{{2}}\sin \frac{{{5}\pi }}{{2}}t, $$

(B4b)

$$ \alpha (t) = - a_{1} \frac{{\pi^{{2}} }}{{4}}\cos \frac{\pi t}{{2}} - a_{2} \pi^{2} \cos \pi t - a_{3} \frac{{{9}\pi^{{2}} }}{{4}}\cos \frac{{{3}\pi t}}{{2}} - a_{{4}} {4}\pi^{2} \cos {2}\pi t - a_{5} \frac{{{25}\pi^{{2}} }}{{4}}\cos \frac{{{5}\pi t}}{{2}}, $$

(B4c)

where $a_{0} ,$ $a_{1} ,$ $a_{2} ,$ $a_{3} ,$ $a_{4} ,$ and $a_{5}$ are the unknown coefficients to be determined by initial- and final-time conditions. When the initial- and final-time conditions are $\theta (0) = 0,$ $\theta (1) = 1,$ $\omega (0) = 0,$ $\omega (1) = 0,$ $\alpha (0) = 0,$ and $\alpha (1) = 0,$ the coefficients can be solved as follows:

$$ \begin{aligned} & \theta (0) = a_{0} + a_{1} + a_{2} + a_{3} + a_{4} + a_{5} = 0,\quad \theta (1) = - a_{2} + a_{4} = 1, \\ & \omega (0) = 0,\quad \omega (1) = - a_{1} + 3a_{3} - 5a_{5} = 0, \\ & \alpha (0) = a_{1} + 4a_{2} + 9a_{3} + 16a_{4} + 25a_{5} = 0,\quad {\text{and}}\;\alpha (1) = a_{2} - 4a_{4} = 0. \\ \end{aligned} $$

It is seen that there are five initial- and final-time conditions, and six unknown coefficients ($a_{0} ,$ $a_{1} ,$ $a_{2} ,$ $a_{3} ,$ $a_{4} ,$ and $\, a_{5}$), one also can not exactly solve the six unknown coefficients by using the cosine form of Fourier series.