1 Introduction

The lower limb of the typical power-assisted Hip exoskeleton robot has a great usage in strength augmentation for efficiently performing works such as walking, running, carrying loads, etc. It employs a hydraulic rotary actuator to accomplish those tasks [1]. In general, electrohydraulic servo systems have a great indispensable role in many applications where large torque load and inertia have to be controlled with high degree of accuracy and efficient performance. They are suitable for a wide range of applications where large torque load is required for the virtue of their distinguished practical features such as small size-to-power ratio, large force output capability and fast response [2].

Inherent nonlinearities, accumulated uncertainties because of the existing friction between moving parts, liquid leakages, volume change and temperature variation of the liquid are considered the major drawbacks of the electrohydraulic servo system [3,4,5]. Modelling and controlling of these systems become very difficult in return. Therefore, the development of a precise control schemes and algorithms has drawn significant efforts of engineers and researchers [5,6,7]. In [8], sliding mode control was presented as a solution for the huge uncertainties and unmodeled dynamics in the models of electrohydraulic systems. Similarly, in [9, 10] SMC was implemented for systems with parameters nonlinearities, modelling uncertainty and external disturbances. SMC, on the other hand, is often combined with other controller scheme to further improve the system performance and to eliminate the most critical drawback of the SMC called chattering which is caused by the high-frequency switching SMC, switching imperfection, delays in switching and small-time constants of the actuators [11,12,13].

Large dead time is another critical drawback of the electrohydraulic servo system that deteriorates the effort of SMC control. This phenomenon occurs frequently in many mechanical and electrical processes. It complicates the analytical analysis and the design of a controller becomes more complicated [14]. Furthermore, the presence of time delay leads to system instability and closed loop performance degradation [15]. various control approaches encounter excessive challenge to stabilize systems with large time delay. Although some controllers can stabilize these systems, it takes long settling time and undesired oscillation may occur in transient process. Therefore, dead time compensation techniques have drawn significant research interest in the past few years. The delay compensation techniques guarantee that the controller designed for the system in the absence of time delay can be used when delay exists [16, 17]. In [18], A robust control scheme for systems with large dead time delay based on disturbance observer technique was proposed. It solves the linear matrix inequalities (LMIs) for the design parameters of the disturbance observer. Similarly, in [19], A robust control scheme for discrete time delayed uncertain systems based on disturbance observer technique was proposed. A new time delay compensator called the modified Smith predictor that is simple in structure and easily tuned manually was proposed in [20]. It provided acceptable performance regardless of uncertainties of the process parameters. In addition, It uses a general technique to estimate instantaneous uncertainties in the control gain, time constant, and time delay. A new version of Smith predictor that uses dynamical compensation and new disturbance rejection is introduced in [15]. Dead time delay analysis was provided to explain how it affects systems and adaptive Smith predictor was proposed for obtaining acceptable control performance even as the time delay significantly increases. The combination of Smith predictor architecture with Sliding mode design was proposed in [21] and [22], it achieved robustness, delay compensation and elimination of modeling errors arises from the delay-free model chosen when controller was designed. It removes the delay out of the closed control loop, and stabilizes the system.

In this paper, a Sliding Mode Controller based on Smith predictor (SMC-SP) is adapted for the control of electro hydraulic servo system. Smith predictor structure offers good control for processes with a large time delay. Thus, when combining a Smith predictor and SMC approach it provides a more advantageous structure for controlling the nonlinear electrohydraulic servo system. The resulted controller counts for the time delay and the system uncertainties to ensure a good performance and stable systems. The unmodeled uncertainties and disturbances have a negligible effect on the system due to the virtue of SMC. SMC-SP compensates the time delay to guarantee robustness against delay as well as nonlinearity and uncertainty of the system. Lastly, position tracking control is performed and comparison between the response of the SMC and SMC-SP systems under the existence of a variety of delay at the output is shown.

The organization of the paper is as follows. Section II describes the mechanical and mathematical model of the electrohydraulic servo system. Then, the derivation of the SMC, and the predictive scheme is given in Section III. Results and discussion for simulation works are presented in section IV.

2 Problem formulation

2.1 System dynamics and modelling

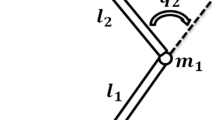
Rotary electro-hydraulic actuator used in the hip of the exoskeleton to assist human walk is discussed in this paper [1]. It is mainly composed of a double-ended hydraulic curved piston rod, a center-mounted rotating shaft, an angular displacement sensor, a guide sleeve, two rigid links attached to the rotating shaft and an electrohydraulic proportional servo valve. In addition to some indispensable sealing components to prevent oil’s internal and external leakages (Figs. 1 and 2).

Fig. 1
figure 1

Layout structure of the electrohydraulic system

Full size image
Fig. 2
figure 2

Rotary Electrohydraulic actuator

Full size image

The dynamical model for the rotary actuator can be represented via Newton’s law by the following Equations as described in [10, 21].

$$ mR_{2}^{2} \ddot{\theta } = \left( {P_{1} \varOmega_{1} - \varOmega_{2} P_{2} } \right)R_{1} - bR_{1} \dot{\theta } - T_{L} . $$
(1)

R1 and R2 are the normal distance from the center of rotation to the rotating piston and the centroid of the load mass respectively. Ω1 and Ω2 is the effective ram area of the cylinder. m is the mass of the load and actuator; b is the damping coefficient and θ is the angular displacement.

The ratio between the effective area at both ends of the asymmetric cylinder is

$$ \eta = \frac{{\varOmega_{2} }}{{\varOmega_{1} }} $$
(2)

Hence PL= P1-ηP2, and the moment of inertia of the rotating load mass is

$$ {\text{J}} = {\text{mR}}_{2}^{2} $$
(3)

Assuming that (R1= R2), dynamical model for the cylinder becomes

$$ J\ddot{\theta } = P_{L} \varOmega_{1} R - bR\dot{\theta } - T_{L} $$
(4)

The load flow QL is defined as

$$ Q_{L} = \frac{{Q_{1} + \eta Q_{2} }}{{1 + \eta^{2} }} $$
(5)

For an ideal electro hydraulic servo valve with symmetric and matched orifice, the load pressure PL and flow QL can be expressed according to the flowing relationship:

$$ Q_{L} = C_{d} wx_{v} \sqrt {\frac{{P_{s} - sgn\left( {x_{v} } \right)P_{L} }}{\rho }} $$
(6)

where, Cd is the valve discharge coefficient, w is the spool valve area gradient, Ps is the supply pressure and ρ is the fluid density.

Applying the continuity equation to the fluid flow at each chamber yields,

$$ \left\{ {\begin{array}{*{20}c} {Q_{1} = \varOmega_{1} R\dot{\theta } + \frac{{V_{1} }}{{\beta_{e} }}\dot{P}_{1} + C_{i} \left( {P_{1} - P_{2} } \right) + C_{e} P_{1} } \\ {Q_{2} = \varOmega_{2} R\dot{\theta } + \frac{{V_{2} }}{{\beta_{e} }}\dot{P}_{2} + C_{i} \left( {P_{1} - P_{2} } \right) - C_{e} P_{2} } \\ \end{array} } \right. $$
(7)

Ci, Ce are the internal and external leakage coefficients respectively. V1 and V2 are the volumes of the cylinder chambers. βe is the effective bulk modulus of oil.

From Eqs. (5) and (6) the load flow is:

$$ Q_{L} = \frac{{Q_{1} + \eta Q_{2} }}{{1 + \eta^{2} }} = \varOmega_{1} R\dot{\theta } + C_{tp} P_{L} + \frac{{V_{t} }}{{2\left( {1 + \eta^{2} } \right)\beta_{e} }}\dot{P}_{L} + C_{ts} P_{s} $$
(8)

where

$$ \left\{ {\begin{array}{*{20}c} {C_{tp} = \frac{1 + n}{{1 + \eta^{3} }}C_{i} + \frac{1}{{1 + \eta^{2} }}C_{e} } \\ {C_{ts} = \frac{{\eta^{2} \left( {\eta^{2} - 1} \right)}}{{\left( {1 + \eta^{2} } \right)\left( {1 + \eta^{3} } \right)}}C_{e} } \\ \end{array} } \right. $$
(9)

Vt is the total volume of actuator and the connecting pipes.

Rearranging Eq. (7), the load pressure of the cylinder is represented by

$$\frac{{{V_t}}}{{2(1 + {\eta ^2}){\beta _e}}}{P_L} = - {\Omega _1}R\theta - {C_{tp}}{P_L} - {C_{ts}}{P_s} + {Q_L}$$
(10)

The dynamics of the spool valve is described by

$$ \tau_{v} \dot{x}_{v} = - x_{v} + K_{v} u $$
(11)

where τv is related to the current input (u = i), τv and Kv are the time constant and gain of the servo valve. The natural frequency of the servo valve is greater than that of the circular hydraulic cylinder, so that the spool valve dynamics is neglected and we have.

$$ x_{v} = K_{v} u . $$
(12)

Substituting Eq. (12) to Eq. (6) and choosing\( u_{0} = \sqrt {P_{s} - sgn\left( {x_{v} } \right)P_{L} } u \),the load flow in Eq. (4) becomes

$$ Q_{L} = \frac{{C_{d} wK_{v} }}{\sqrt \rho }u_{0} $$
(13)
$$ \frac{{V_{t} }}{{2\left( {1 + \eta^{2} } \right)\beta_{e} }}\dot{P}_{L} = - \varOmega_{1} R\dot{\theta } - C_{tp} P_{L} + \frac{{C_{d} wK_{v} }}{\sqrt \rho }u_{0} - C_{ts} P_{s} $$
(14)

Combining Eqs. (4), (7)—seeking of simplicity the valve dynamics is neglected—the 3rd order model is obtained for the robust sliding mode controller. The system states are selected as:

$$ \left[ {x_{1} x_{2} x_{3} } \right]^{T} = \left[ {\theta \dot{\theta } P_{L} } \right]^{T} $$
(15)

and the state space representation of the system is shown below, here J is the inertia of piston and load.

$$ \left\{ \begin{aligned} \dot{x}_{1} = x_{2} \hfill \\ \dot{x}_{2} = - \phi_{1} x_{2} + \phi_{2} x_{3} \hfill \\ \dot{x}_{3} = - \psi_{1} x_{2} - \psi_{2} x_{3} + Hu_{0} - C_{ts} P_{s} + T_{L} \hfill \\ \end{aligned} \right. . $$
(16)
$$ \left\{ {\begin{array}{*{20}c} {\phi_{1} = \frac{bR}{J} } \\ {\phi_{2} = \frac{{\varOmega_{1} R}}{J} } \\ {\psi_{1} = \frac{{2\left( {1 + \eta^{2} } \right)\beta_{e} \varOmega_{1} R}}{{V_{t} }} } \\ {\psi_{2} = \frac{{2\left( {1 + \eta^{2} } \right)\beta_{e} C_{tp} }}{{V_{t} }} } \\ {H = \frac{{2\left( {1 + \eta^{2} } \right)\beta_{e} C_{d} wK_{v} }}{{V_{t} \sqrt \rho }} } \\ \end{array} } \right. $$
(17)

Since, sgn(u0) = sgn(u), then the actual input of the system is

$$ u = \frac{{u_{0} }}{{\sqrt {P_{s} - \text{sgn} \left( {u_{0} } \right)x_{3} } }} $$
(18)

2.2 Smith predictor

Smith predictor configuration shown in Fig. 3, uses the identified dynamics of the system that model the delay free part and a delay compensator. In this experiment the delay compensator was modeled as a transport delay.

Fig. 3
figure 3

SMC-SP Controller Schematic Diagram

Full size image

Nonlinear dynamics features of the lower limb actuator relays on time-varying working-points that can be locally linearized. The control signal passes into two analogous parallel paths. Smith predictor branch estimates the delay-free response of the system. Then, this prediction is compared to the desired setpoint and the resulted error signal is delivered to the controller to calculate the needed adjustments and decide the required control action. Smith predictor eliminate the effects of dead time delay effectively.

The nonlinear model of the electrohydraulic servo system is factorized into

$$ G\left( s \right) = y_{m} \left( s \right) e^{ - \tau s} $$
(19)

\( G\left( s \right) \) is the plant model, ym(s)* is the estimated delay-free part of the model expressed in Eq. (16), and e−ts is the time delay compensator and the output of Smith predictor can be written as:

$$ Y\left( s \right) = y_{m} \left( s \right) u\left( s \right) + y_{p} \left( s \right) u\left( s \right) - y_{m} \left( s \right) e^{ - \tau s} u\left( s \right) $$
(20)

Remark 1

if \( y_{m} \left( s \right) = y_{p} \left( s \right) \), then SMC-SP eliminates the delay effects and achieve a satisfying performance.

Remark 2

Uncertainty and nonlinearity of the process complicated getting precise model which may lead to deteriorating the performance.

The design of the SMC-SP in the following section is facilitated be this factorization.

2.3 Sliding mode controller design

SMC is a nonlinear controller that provides a robust control action for nonlinear systems that exhibit uncertainties in its parameters [22]. SMC design procedure follows two steps, the design of a sliding stable surface and the design of a control law to drive the system states onto the required. The objective of this section is to develop a SMC for the nonlinear EHS based on the second order system represented by the state space in the previous section. However, several types of disturbances, nonlinearity may exist that are not explicitly represented on the linearized model in Eq. (16).

In Fig. 3, the error E(t) is the difference between the desired input trajectory R(t) and the actual delay compensated response Y(t). A control rule is designed to guarantee finite time reaching of sliding surface even in the presence of disturbances and mismatches. In this work, the sliding surface S(t), defined by [23], has been adopted to achieve the stability and tracking performance.

Fig. 4
figure 4

Output angular trajectory (Time delay 0.1 s)

Full size image

Firstly, the sliding surface is defined as

$$ S_{0} = e_{1} + \lambda_{1} e $$
(21)

Where e = Y(t) – R(t), when differentiating \( S_{0} \) the control input u will not appear in the derived function because the relative degree between u and \( s_{0} \) is greater than one. Then, the sliding surface is chosen to be the following function with a relative degree equal to one between u and S.

$$ S = e_{2} + \lambda_{2} e_{1} + \lambda_{1} e $$
(22)

the corresponding error of the system states and its derivative are

$$ \begin{aligned} \left\{ {\begin{array}{*{20}c} {e = x_{1} - \theta_{d} } \\ {e_{1} = x_{2} - \dot{\theta }_{d} } \\ {e_{2} = \dot{x}_{2} - \ddot{\theta }_{d} } \\ \end{array} } \right. \\ \dot{e}_{2} & = \ddot{x}_{2} - \dddot \theta_{d} = \left( { - \phi_{1} \dot{x}_{2} + \phi_{2} \dot{x}_{3} } \right) - \dddot x_{d} \\ & \quad = \left( { - \phi_{1} \left( { - \phi_{1} x2 + \phi_{2} x_{3} } \right) + \phi_{2} \left( { - \psi_{1} x_{2} - \psi_{2} x_{3} + Hu_{0} } \right)} \right) - \dddot \theta_{d} \\ \end{aligned} $$
(23)
$$ \dot{e}_{2} = \left( {\phi_{1}^{2} - \phi_{2} \psi_{1} } \right)x_{2} - \left( {\phi_{1} \phi_{2} + \phi_{2} \psi_{2} } \right)x_{3} + \left( {\phi_{2} H} \right)u_{0} - \dddot \theta_{d} . $$
(24)

The control input u appeared when differentiating the sliding surface function. Furthermore, λ1, λ2 are positive constants to drive the system states towards the sliding surface and remain there hence ensure the stability of the system. When the switching function reaches its zero level the states will approach the origin as well [24].

The sliding mode control law ensures the states are driven to zero (towards the sliding surface) is determined such that both reaching phase and sliding phase is SṠ < 0.

$$ \dot{s} = \dot{e}_{2} + \lambda_{2} e_{2} + \lambda_{1} e_{1} $$
(25)

The equivalent control is selected by the necessary condition of sliding mode to exist \( \dot{s} = 0 \) with nominal value.

$$ u_{eq} = \left( {\phi_{2} H} \right)^{ - 1} \left( { - \left( {\phi_{1}^{2} - \phi_{2} \psi_{1} } \right)x_{2} + \left( {\phi_{1} \phi_{2} + \phi_{2} \psi_{2} } \right)x_{3} + \dddot \theta_{d} - \lambda_{2} e_{2} - \lambda_{1} e_{1} } \right) $$
(26)

The control rule is designed to meet the sliding condition regardless the estimation of errors. Hence, a discontinuous term is added to Eq. (26),

$$ u = u_{eq} + u_{sw} $$
(27)

Where

$$ u_{sw} = K sgn\left( s \right) $$
(28)

Remark 3

SMC is chosen for its robustness against parameters uncertainty and external disturbances.

Achieving trajectories tracking with zero error requires all system states to be forced to converge to S in finite time and remain on S afterwards. For the system stability the Lyapunov function candidate is chosen as:

$$ V = 0.5 S^{2} , $$
(29)

Differentiating Ѵ along the closed loop Eq. (16) and θ is assumed to be constant θ ∊ R,

$$ \left\{ {\begin{array}{*{20}c} {e = x_{1} - \theta_{d} } \\ {e_{1} = x_{2} - \dot{\theta }_{d} = x_{2} } \\ {e_{2} = \dot{x}_{2} - \ddot{\theta }_{d} = \dot{x}_{2} } \\ \end{array} } \right. $$
(30)
$$ \dot{V} = {\text{s}}\left( { - \psi_{1} x_{2} - \psi_{2} x_{3} + Hu_{0} + \lambda_{2} \left( { - \phi_{1} x_{2} + \phi_{2} x_{3} } \right) + \lambda_{1} \left( {x_{2} } \right)} \right) $$
(31)

Substituting the control law in Eq. (27), then reaching condition of SMC is obtained where \( K \) is a positive design parameter. Hence,

$$ \dot{V} \le - {\text{K}}\left| S \right| $$
(32)

The switching gain K of the discontinuous part of the controller rule is determined such that if it is met, reaching condition will be achieved and the tracking will be done within certain specified error bounds, and the closed loop system is asymptotically stable.

For the SMC-SP controlled systems, the delay time is supposed to be compensated by the Smith predictor. The stability analysis of the designed SMC presented above is applied. The system uncertainty caused by modelling error is represented by ξ (χ, u, t) which is introduced to Eq. (31) but has no significant effects on the system stability.

Remark 4

Initially, the system is modeled according to its parameters’ nominal values and the errors are considered as system uncertainty. SMC-SP eliminates the effects of time delay. As a result, the system stability is mainly guaranteed by the SMC.

3 Experimental results and discussion

The experiment was performed on a real-time control platform. The platform of the rotary electrohydraulic servo system is mainly composed of pressure supply unit, Rotary hydraulic actuator, angular displacement sensor, electro hydraulic servo valve (FF101-6, AVIC) and a real time control system installed on a computer (IPC-610L, Advantech Inc.). Tables 1 and 2 show the relevant system and controller parameters.

Table 1 Nominal equivalent of the EHS parameters
Full size table
Table 2 SMC Controller Parameter
Full size table

The proposed controller scheme was tested for two types of trajectories; continuous sinusoidal motion and a step positioning. The experiment was repeated many times for different dead time.

Experimental results shown in this section clearly prove the feasibility and the efficiency of the proposed SMC-SP scheme. High-frequency oscillations triggered by large dead time delay is eliminated by the utilization of SMC-SP scheme. The results also demonstrate the significant performance improvements of the proposed scheme in terms of steady state error stability.

The desired and the actual trajectories shown in Figs. 4 and 5, proves the effectiveness of the proposed method. It graphically compares the response of systems controlled by the proposed SMC-SP scheme with other control scheme under the presence of dead time delay. The proposed SMC-SP scheme achieves a smooth and stable tracking with less steady state error and minimum overshoot peak value. In contrast, the performance of systems solely controlled by SMC was degraded and undesired attenuation was fired when large dead time exists.

Fig. 5
figure 5

Output angular trajectory (Time delay 0.05 s)

Full size image

It can be noticed that as the dead time increase the stability of the system cannot be maintained. On the other hand, this issue is totally minimized and delay time effect is eliminated by the use of the proposed scheme of SMC-SP scheme. The delay time in Fig. 6 is less than that in Fig. 4. As a result, the steady state response of the SMC controlled system has better performance in compare to that in Fig. 4 but smooth response is only obtained through the use of the proposed SMC-SP scheme where the effect of delay is eliminated.

Fig. 6
figure 6

Difference between desired and actual trajectories (SMC, SMC-SP) for different time delay

Full size image

The stability of the SMC controlled systems can’t be maintained when there exists a large dead time. Furthermore, the steady state error of the SMC controlled systems in the case of 0.1 s time delay is extremely large in compare to the 0.05 s delay time as shown in Fig. 5 and Fig. 6 respectively. It can be concluded that, time delay or large dead time has a great effect on the system closed-loop dynamics as well as the steady state response. The steady state error increases as the dead time of the system increases. Furthermore, the amplitude of the undesired fluctuation gets larger as the dead time increases and this increase the risk of damaging the mechanical parts of the actuator as they may exceed the natural frequency of the system. The compensation of large delay time through the application of the proposed SMC-SP scheme ensures the mitigation of all these negative impacts. Figure 6, shows the error signal (difference between the desired and corresponding actual trajectory). Undesired fluctuation in the response of delayed SMC controlled affect both stability and steady state error of the system. In contrast, the SMC-SP controlled system’s response is stable and has lower steady state error than delayed SMC’s response.

Fig. 7
figure 7

Output angular position (for different time delays)

Full size image

Regardless of the type of desired input, the negative impacts of large delay time exist. Figures 7, 8 and 9, show the system response when the desired position is in the form of step command. The system stability is degraded from asymptotically stable to marginally stable. These fluctuation or high frequencies underdamped oscillation increase the risk of damaging the mechanical parts of the actuator as they may exceed the natural frequency of the system. On the other hand, the amplitude of underdamped oscillation can be bounded from exceeding certain range.

Fig. 8
figure 8

Output angular position (for different time delays)

Full size image
Fig. 9
figure 9

Control Signal (u)

Full size image

4 Conclusion

This paper illustrates the development and experimental validation of a delay compensating controller SMC-SP for the rotary electro-hydraulic actuator used in the lower limb of the power-assisted hip exoskeleton. Generally, a trivial transport delay in the output of an electro-hydraulic servo system fire undesired attenuation and drive the system to be unstable. However, the designed technique compensates the dead time delay occurring in the output and alleviate its effect. The obtained experimental results show good transient and steady state performance in terms of rise time, steady state error, maximum overshoot and stability of the system. The main contribution of this paper was improving a new control technique that counts for the large dead time phenomenon problem. The proposed scheme guarantee that the system stability is maintained and the performance of the system is not affected by the large dead time occurring in the output. The efficiency of this method is validated experimentally and compared with other controllers.