A novel intelligent fast terminal sliding mode control for a class of nonlinear systems: application to atomic force microscope

Abstract

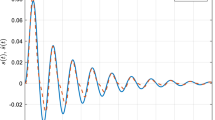
This paper addresses the problem of finite-time robust control using an intelligent fast terminal sliding mode control method for a class of nonlinear systems in presence of bounded uncertainty and disturbance. In the proposed method, adaptive neuro-fuzzy inference systems are utilized to determine some parameters in the nonlinear sliding surface based on the measured value of the sliding surface and the system error at each time and thereby variable nonlinear sliding surface is provided. Furthermore, an intelligent optimization algorithm namely honey bee algorithm is also applied to determine the optimal weights of the neuro-fuzzy network. Finite time convergence with increased speed and also chattering-free response are the main advantages of the proposed method compared with the conventional terminal sliding mode control methods. The proposed controller is applied to an atomic force microscope in attendance of uncertainty and disturbance. The simulation results demonstrate considerable success of the method, and show that the error reaches zero in a very short time without chattering.

Appendices

Appendix A: Proof of Theorem 1

In order to prove the theorem, we consider the following Lyapunov function:

$$\begin{aligned} v=\frac{1}{2}s_{n-1}^2 \end{aligned}$$

(A.1)

Therefore, its derivative becomes:

$$\begin{aligned} \dot{v}=\dot{s}_{n-1} s_{n-1} \end{aligned}$$

(A.2)

Fig. 12

ANFIS structure with single input and single output

Substituting (10) into (A.2), we have:

$$\begin{aligned} \dot{v}= & {} \left[ \Delta f(\mathbf{x})+d(\mathbf{x})-l\hbox {sign}(s_{n-1} )\right] s_{n-1}\nonumber \\\le & {} -\left[ l-(\delta _1 +\delta _2 )\right] \left| {s_{n-1} } \right| \end{aligned}$$

(A.3)

Thus, if $l>\delta _1 +\delta _2$, $\dot{v}<0$ and the proof of convergence is completed. Now, we prove the convergence can be reached in finite time. We rewrite (A.3) as:

$$\begin{aligned} \dot{v}=\frac{1}{2}\frac{d}{dt}s_{n-1}^2 \le -\left[ l-(\delta _1 +\delta _2 )\right] \left| {s_{n-1} } \right| \end{aligned}$$

(A.4)

Assuming that $t_1$ is the time of reaching $s_{n-1}$ to zero (i.e., $s_{n-1} (t_1 )=0)$, by integrating (A.4) form $t_0$ to $t_1$, it can be written that:

$$\begin{aligned} -\left| {s_{n-1} (t_0 )} \right| \le -\left[ l-(\delta _1 +\delta _2 )\right] (t_1 -t_0 ) \end{aligned}$$

(A.5)

Therefore, for $l>\delta _1 +\delta _2$, we have:

$$\begin{aligned} t_{s_{n-1} } =t_1 -t_0 \le \frac{\left| {s_{n-1} (t_0 )} \right| }{l-(\delta _1 +\delta _2 )} \end{aligned}$$

(A.6)

Thus, $s_{n-1}$ will reach zero in finite time of (A.6) and will remain zero thereafter.

Appendix B: ANFIS structure

ANFIS structure consists of antecedent and conclusion sections. These two sections are connected to each other through fuzzy rules. We consider a set of m rules of the following form:

$$\begin{aligned} \hbox {IF}~v~\hbox {is}~A_i~\hbox {THEN}~z~\hbox {is}~k_i v+r_i\quad \hbox {for}\quad i=1,2,\ldots ,m \end{aligned}$$

(B.1)

where $A_i$ are the fuzzy sets and $r_i$ are the acceptable real values.

The ANFIS architecture includes five layers and involves single input and single output as depicted in Fig. 12.

The layers of the ANIFS are described as follows [31]:

Layer 1. Fuzzifier layer This layer provides the MFs for each input. In this paper, triangular MF is used and described by:

$$\begin{aligned}&\mu _{A_i}(v)=\hbox {trimf}(v;a_i,b_i ,c_i )\nonumber \\&\qquad \qquad =\max \left( \min \left( {\frac{v-a_i }{b_i -a_i },\frac{c_i -v}{c_i -a_i }} \right) ,0 \right) ;\nonumber \\&\qquad \qquad \qquad i=1, 2,\ldots , m\end{aligned}$$

(B.2)

$$\begin{aligned}&O_i^1 =\mu _{A_i } (v) \end{aligned}$$

(B.3)

The shape of each MF is determined using the parameters $a_i,b_i,c_i$ for $i=1,2,\ldots ,m$. The parameters in this layer are called antecedent parameters.

Layer 2. Rule layer The rule layer indicates firing strength for each rule that is produced in fuzzifier layer. For multi input systems with $m_j$ fuzzy sets for each input, there exist $m=\mathop {\pi }\limits _{j}m_j$ rules. For single input system the maximum number of rules can be $m=m_1$ rules, and therefore, the output of Layer 2 is same as the Layer 1.

$$\begin{aligned} O_i^2 =w_i =\mu _{A_i } (v);\quad i=1,2,\ldots ,m \end{aligned}$$

(B.4)

where $\mu _{A_i}(v)$ is the value of membership of v in the fuzzy set $A_i$.

Layer 3. Normalization layer This layer is the normalized firing strength for each input. This normalization is the ratio of the i-th rule firing strength to the total firing strength, i.e.:

$$\begin{aligned} O_i^3 =\bar{w}_i =\frac{w_i}{\sum _{i=1}^m {w_i}};\quad i=1,2,\ldots ,m \end{aligned}$$

(B.5)

Layer 4. Defuzzifier layer The output of each node in this layer is achieved by multiplying a polynomial with normalized firing strength and is calculated as follow:

$$\begin{aligned} O_i^4 =\bar{w}_i f_i =\bar{w}_i (k_i v+r_i);\quad i= 1,2,\ldots ,m \end{aligned}$$

(B.6)

The output of this layer is normalized. $r_i$ in this layer denotes the conclusion parameter.

Layer 5. Summation layer This layer is obtained from the sum of all received signals.

$$\begin{aligned} O_i^5= & {} z=\sum _{i=1}^m {\bar{w}_i f_i } =\sum _{i=1}^m {\bar{w}_i (k_i v+r_i )} \nonumber \\= & {} \frac{\sum _{i=1}^m {w_i (k_i v+r_i )}}{\sum _{i=1}^m {w_i } } =\frac{\sum _{i=1}^m {\mu _{A_i } (v)(k_i v+r_i )}}{\sum _{i=1}^m {\mu _{A_i } (v)} };\nonumber \\&i=1, 2,\ldots ,m \end{aligned}$$

(B.7)

Appendix C: Proof of Theorem 2

Similar to Theorem 1, we consider the following Lyapunov function:

$$\begin{aligned} v=\frac{1}{2}s_{n-1}^2 \end{aligned}$$

(C.1)

Its derivative is:

$$\begin{aligned} \dot{v}=\dot{s}_{n-1} s_{n-1} \end{aligned}$$

(C.2)

Substituting (23) into (C.2), we have:

$$\begin{aligned} \dot{v}= & {} \left[ \Delta f(\mathbf{x})+d(\mathbf{x})-l_{\mathrm{ANFIS}} (t)\right] s_{n-1}\nonumber \\< & {} -\left[ \frac{l_{\mathrm{ANFIS}} (t)}{\hbox {sign}(s_{n-1} )}-(\delta _1 +\delta _2 )\right] \left| {s_{n-1} } \right| \end{aligned}$$

(C.3)

Since ANFIS with function of $l_{\mathrm{ANFIS}} (s_{n-1} )$ has been used as universal approximator for $l\hbox {sign}(s_{n-1} )$, its sign is same as $l\hbox {sign}(s_{n-1} )$. Therefore, we have:

$$\begin{aligned} \dot{v}<-\left[ \left| {l_{\mathrm{ANFIS}} (t)} \right| -(\delta _1 +\delta _2 )\right] \left| {s_{n-1} } \right| \end{aligned}$$

(C.4)

Thus, if $\left| {l_{\mathrm{ANFIS}} (t)} \right| >\delta _1 +\delta _2$, $\dot{v}<0$ and the proof of convergence is completed. Now, we prove the convergence can be reached in finite time. Substituting (12) into (C.4):

$$\begin{aligned} \frac{1}{2}\frac{d}{dt}s_{n-1}^2 \le -\left[ \left| {l_{\mathrm{ANFIS}} (s_{n-1} )} \right| -(\delta _1 +\delta _2 )\right] \left| {s_{n-1} } \right| \end{aligned}$$

(C.5)

Assuming $t_1$ as the time of reaching $s_{n-1}$ to zero (i.e., $s_{n-1} (t_1 )=0)$, by integrating (C.4) form $t_0$ to $t_1$, we can obtain:

$$\begin{aligned} -\left| {s_{n-1} (t_0 )} \right| \le -\left[ \left| {l_{\mathrm{ANFIS}} (s_{n-1} )} \right| -(\delta _1 +\delta _2 )\right] (t_1 -t_0 ) \end{aligned}$$

(C.6)

For $l_{\mathrm{ANFIS}} (s_{n-1} )>\delta _1 +\delta _2$, we have:

$$\begin{aligned} t_{s_{n-1} } =t_1 -t_0 \le \frac{\left| {s_{n-1} (t_0 )} \right| }{\left| {l_{\mathrm{ANFIS}} (s_{n-1} )} \right| -(\delta _1 +\delta _2 )} \end{aligned}$$

(C.7)

Therefore, $e_i$, for $i=1,2,\ldots ,n$ will reach zero in finite time and will remain zero thereafter.

Appendix D: Bee algorithm

BA is inspirited from behavior of the honey bee in the nature. In this paper, a BA based on foraging behavior of bees is used due to its short computation time and also quick convergence time. The aim of BA in nature is to find the best location among the food sources (flower patches) to harvest nectar or pollen. The algorithm needs a number of parameters to be defined as shown in Table 2.

Table 2 Parameters of BA

The algorithm is described as below [32]:

Search space and fitness function In evolutionary algorithms, the main goal is to minimize fitness or cost function and to search for the optimal points in the feasible solutions in the search space. The search space is defined as $U=\{\mathbf{p}\in \mathfrak {R}^{n};p_{i,\min }<p_i <p_{i,\max }, i=1, 2, \ldots , n\}$ where $p_i$ can be considered as one of n parameters to be determined by BA in the search space of parameters and a fitness function is also considered as $f(\mathbf{p}):U\rightarrow \mathfrak {R}$, which in this paper has been defined in (25). In addition, each solution candidate is defined as a n-dimensional variable $\mathbf{p}=[p_1,p_2,\ldots ,p_n ]^{T}$.

Initialization The algorithm starts with $n_s$ scout bees propagated with uniform probability in the problem solution space. Each scout bee evaluates its position through the fitness function. Then, the algorithm enters the main cycle, which consists of four steps. The algorithm stops when the termination criterion of the algorithm is satisfied.

Waggle dance The $n_s$ locations visited by scout bees are ranked according to fitness function, and then $n_b$ best locations with highest fitness (i.e. with minimum cost) are chosen by local search. Each of the scout bees that come back from the $n_b$ superior locations performs a waggle dance to inform worker bees about the local search of the best locations. For each $n_e$ first top rated elite locations identified by scout bees among $n_b$ best available sites, $n_{re}$ worker bees are sent to search in the neighborhood of these sites. Then, for each $n_b -n_{re}$ remaining locations $(n_{rb} <n_{re} )$, forager bees are sent for a local search. According to this method, most of worker bees are allocated for searching in locations with highest fitness. Thus, local search is performed with more accuracy in the vicinity of these elite sites that are most probable points in the solution space.

Local search The local search is carried out by worker bees or foragers so that these bees steer to the vicinity of site selected by scout bee. For each location, the fitness is calculated by worker bees. The radius of this location is $n_{gh}$, which has been initialized at the beginning of the problem. If the fitness of one of the worker bee is higher than that of the scout bee, the selected worker bee will be chosen as the new scout bee. At the end, the best bee with the highest fitness is remained for each flower patch. These bees are selected as representatives of the flower patches, and return to the hive to do the waggle dance.

Global search In this step, $(n_s -n_b )$ bees are spread randomly as scout bees for finding new flower patches in the whole problem solution space. Selection of scout bee in a random process is for exploring better sites by BA and indicates the efficiency of BA in solving problems.

Population update At the end of each iteration, the new population of the bee’s colony consists of two groups. The first group includes $n_b$ scout bees correspondent with the center the representatives (the best available solution) of each flower patch and denotes the local search. The second group consists of $(n_s -n_b )$ scout bees correspondent with solutions that are produced randomly in the problem’s solution space, and shows the results of the global search of the algorithm.

Termination condition The termination criterion depends on the problem’s conditions, and can be either a predefined f.