Skip to main content
SpringerLink
Log in

Nonlinear behavior of a novel chaotic jerk system: antimonotonicity, crises, and multiple coexisting attractors

  • Published:
International Journal of Dynamics and Control Aims and scope Submit manuscript

Abstract

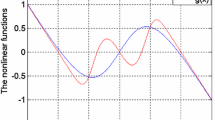
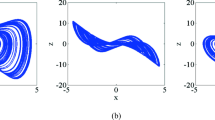
In this contribution, a novel Jerk system with a smooth piecewise quadratic nonlinearity is introduced. The new nonlinearity provides a similar smoothness as the cubic polynomial function, but a faster response and a simpler circuitry. The basic dynamical properties of the model are discussed in terms of its parameters by using standard nonlinear analysis tools including phase space trajectory plots, frequency spectra, bifurcation diagrams and Lyapunov exponent plots. The bifurcation analysis yields very rich and interesting scenarios such as period-doubling bifurcations, antimonotonicity (i.e. the concurrent creation and annihilation of periodic orbits), periodic windows, and symmetry recovering crises. One of the main findings of this work is the presence of a window in the parameter space in which the novel jerk system experiences the unusual and striking feature of multiple coexisting attractors (i.e. coexistence of four or six disconnected periodic and chaotic attractors) for the same parameters’ setting. Correspondingly, basins of attraction of various competing attractors display extremely complex basin boundaries. Compared to some lower dimensional systems (e.g. Leipnik–Newton system, modified Sprott B system) capable of displaying such type of behavior reported to date, the jerk system introduced in this work represents the simplest and the most ‘elegant’ paradigm. An electronic circuit for allowing an illustration of the theoretical model is proposed and implemented in PSpice. The results obtained in this work let us conjecture that there exist some regions in its parameter space (that need to be uncovered) in which the universal Chua’s circuit experiences six disconnected non static attractors similar to those presented in this work.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

References

  1. Masoller C (1994) Coexistence of attractors in a laser diode with optical feedback from a large external cavity. Phys Rev A 50:2569–2578

    Article  Google Scholar 

  2. Cushing JM, Henson SM, Blackburn (2007) Multiple mixed attractors in a competition model. J Biol Dyn 1:347–362

    Article  MATH  MathSciNet  Google Scholar 

  3. Upadhyay RK (2003) Multiple attractors and crisis route to chaos in a model of food-chain. Chaos Solitons Fractals 16:737–747

    Article  MATH  MathSciNet  Google Scholar 

  4. Massoudi A, Mahjani MG, Jafarian M (2010) Multiple attractors in Koper–Gaspard model of electrochemical. J Electroanal Chem 647:74–86

    Article  Google Scholar 

  5. Li C, Sprott JC (2014) Coexisting hidden attractors in a 4-D simplified Lorenz system. Int J Bifurc Chaos 24:1450034

    Article  MATH  MathSciNet  Google Scholar 

  6. Leipnik RB, Newton TA (1981) Double strange attractors in rigid body motion with linear feedback control. Phys Lett A 86:63–87

    Article  MathSciNet  Google Scholar 

  7. Guan ZH, Lai Q, Chi M, Chen XM, Liu F (2014) A new three-dimensional system with multiple chaotic attractors. Nonlinear Dyn 75:331–343

    Article  MATH  MathSciNet  Google Scholar 

  8. Lai Q, Chen S (2016) Generating multiple chaotic attractors from sprott B system. Int J Bifurc Chaos 26(11):1650177

    Article  MATH  MathSciNet  Google Scholar 

  9. Lai Q, Chen S (2016) Coexisting attractors generated from a new 4D smooth chaotic system. Int J Control Automation Syst 14(4):1124–1131

    Article  Google Scholar 

  10. Kengne J, Njitacke ZT, Fotsin HB (2016) Dynamical analysis of a simple autonomous jerk system with multiple attractors. Nonlinear Dyn 83:751–765

    Article  MathSciNet  Google Scholar 

  11. Vaithianathan V, Veijun J (1999) Coexistence of four different attractors in a fundamental power system model. IEEE Trans Circuits Syst I 46:405–409

    Article  Google Scholar 

  12. Kengne J (2015) Coexistence of chaos with hyperchaos, period-3 doubling bifurcation, and transient chaos in the hyperchaotic oscillator with gyrators. Int J Bifurc Chaos 25(4):1550052

    Article  MathSciNet  Google Scholar 

  13. Pivka L, Wu CW, Huang A (1994) Chua’s oscillator: a compendium of chaotic phenomena. J Frankl Inst 331B(6):705–741

    Article  MATH  MathSciNet  Google Scholar 

  14. Kuznetsov AP, Kuznetsov SP, Mosekilde E, Stankevich NV (2015) Co-existing hidden attractors in a radio-physical oscillator. J Phys A Math Theor 48:125101

    Article  MATH  MathSciNet  Google Scholar 

  15. Kengne J, Njitacke ZT, Nguomkam Negou A, Fouodji Tsotsop M, Fotsin HB (2015) Coexistence of multiple attractors and crisis route to chaos in a novel chaotic jerk circuit. Int J Bifurc Chaos 25(4):1550052

    Article  MATH  Google Scholar 

  16. Njitacke ZT, kengne J, Fotsin HB, Nguomkam Negou A, Tchiotsop D (2016) Coexistence of multiple attractors and crisis route to chaos in a novel memristive diode bidge-based Jerk circuit. Chaos Solitons Fractals 91:180–197

    Article  MATH  Google Scholar 

  17. Kengne J (2016) On the dynamics of chua’s oscillator with a smooth cubic nonlinearity: occurrence of multiple attractors. Nonlinear Dyn 87(1):363–375

    Article  MathSciNet  Google Scholar 

  18. Bao B, Jiang T, Xu Q, Chen M, Wu H, Hu Y (2016) Coexisting infinitely many attractors in active band-pass filter-based memristive circuit. Nonlinear Dyn 86(3):1711–1723

    Article  Google Scholar 

  19. Maggio GM, De Feo O, Kennedy MP (1999) Nonlinear analysis of the Colpitts oscillator and application to design. IEEE Trans Circuits Syst I Fundam Theory Appl 46:1118–1130

    Article  MATH  Google Scholar 

  20. Li C, Hu W, Sprott JC, Wang X (2015) Multistability in symmetric chaotic systems. Eur Phys J Spec Top 224:1493–1506

    Article  Google Scholar 

  21. Xu Q, Lin Y, Bao’ B, Chen M (2016) Multiple attractors in a non-ideal active voltage-controlled memristor based Chua’s circuit. Chaos Solitons Fractals 83:186–200

    Article  MATH  MathSciNet  Google Scholar 

  22. Tang KS, Man KF (1998) An alternative Chua’s circuit implementation. In: Proceedings of the IEEE international symposium on industrial electronics (ISIE ’98), pp 441–444

  23. Tang KS, Man KF, Zhong GQ, Chen G (2001) Generating chaos via \(x|x|\). IEEE Trans Circuits Syst I Fundam Theory Appl 48(5):636–641

    Article  MATH  MathSciNet  Google Scholar 

  24. Munmuangsaen B, Srisuchinwong B, Sprott JC (2011) Generalization of the simplest autonomous chaotic system. Phys Lett A 375:1445–1450

    Article  MATH  Google Scholar 

  25. Sprott JC (2010) Elegant chaos: algebraically simple flow. World Scientific Publishing, Singapore

    Book  MATH  Google Scholar 

  26. Sprott JC (2000) Simple chaotic systems and circuits. Am J Phys 68:758–763

    Article  Google Scholar 

  27. Sprott JC (1997) Simplest dissipative chaotic flow. Phys Lett A 228:271–274

    Article  MATH  MathSciNet  Google Scholar 

  28. Sprott JC (1997) Some simple Jerk functions. Am J Phys 65:537–543

    Article  Google Scholar 

  29. Sprott JC (2011) A new chaotic jerk circuit. IEEE Trans Circuits Syst II Express Br 58:240–243

    Article  Google Scholar 

  30. Eichhorn R, Linz SJ, Hanggi P (2002) Simple polynomial classes of chaotic jerky dynamics. Chaos Solitons Fractals 13:1–15

    Article  MATH  MathSciNet  Google Scholar 

  31. Strogatz SH (1994) Nonlinear dynamics and chaos. Addison-Wesley, Reading

    Google Scholar 

  32. Nayfeh AH, Balachandran B (1995) Applied nonlinear dynamics: analytical, computational and experimental methods. Wiley, New York

    Book  MATH  Google Scholar 

  33. Kuznetsov YA (1995) Elements of applied bifurcation theory. Springer, New York

    Book  MATH  Google Scholar 

  34. Li C, Sprott JC (2013) Amplitude control approach for chaotic signals. Nonlinear Dyn 73:1335–1341

    Article  MATH  MathSciNet  Google Scholar 

  35. Kuznetsov N, Leonov G, Vagaitsev V (2010) Analytical-numerical method for attractor localization of generalized Chua’s system. IFAC Proc Vol 4(1):29–33

    Article  Google Scholar 

  36. Leonov G, Kuznetsov N, Vagaitsev V (2011) Localization of hidden Chua’s attractors Phys. Lett A 375(23):2230–2233

    Article  MATH  MathSciNet  Google Scholar 

  37. Leonov G, Kuznetsov N, Vagaitsev V (2012) Hidden attractor in smooth Chua systems. Phys D Nonlinear Phenom 241(18):1482–1486

    Article  MATH  MathSciNet  Google Scholar 

  38. Leonov GA, Kuznetsov NV (2013) Hidden attractors in dynamical systems. From hidden oscillations in Hilbert–Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractor in Chua circuits. Int J Bifurc Chaos 23(01):1330002

    Article  MATH  MathSciNet  Google Scholar 

  39. Leonov GA, Kuznetsov NV, Mokaev TN (2015) Homoclinic orbits, and self-excited and hidden attractors in a Lorenz-like system describing convective fluid motion. Eur Phys J Spec Top 224:1421–1458

    Article  Google Scholar 

  40. Wolf A, Swift JB, Swinney HL, Wastano JA (1985) Determining Lyapunov exponents from time series. Phys D 16:285–317

    Article  MATH  MathSciNet  Google Scholar 

  41. Pisarchik AN, Feudel U (2014) Control of multistability. Phys Rep 540(4):167–218

    Article  MATH  MathSciNet  Google Scholar 

  42. Dawson SP, Grebogi C, Yorke JA, Kan I, Koçak H (1992) Antimonotonicity: inevitable reversals of period-doubling cascades. Phys Lett A 162:249–254

    Article  MathSciNet  Google Scholar 

  43. Parlitz U, Lauterborn W (1985) Superstructure in the bifurcation set of the Duffing equation \(\ddot{x}+ d\dot{x}+ x+ x^{3}= \text{ f } \text{ cos } (\omega \text{ t })\). Phys Lett A 107:351–355

    Article  MathSciNet  Google Scholar 

  44. Parlitz U, Lauterborn W (1987) Period-doubling cascades and devil’s staircases of the driven van der Pol oscillator. Phys Rev A 36:1428

    Article  Google Scholar 

  45. Kocarev L, Halle K, Eckert K, Chua L (1993) Experimental observation of antimonotonicity in Chua’s circuit. Int J Bifurc Chaos 3:1051–1055

    Article  MATH  Google Scholar 

  46. Ogawa T (1988) Quasiperiodic instability and chaos in the bad-cavity laser with modulated inversion: numerical analysis of a Toda oscillator system. Phys Rev A 37:4286

    Article  MathSciNet  Google Scholar 

  47. Kyprianidis I, Stouboulos I, Haralabidis P, Bountis T (2000) Antimonotonicity and chaotic dynamics in a fourth-order autonomous nonlinear electric circuit. Int J Bifurc Chaos 10:1903–1915

    Google Scholar 

  48. Manimehan I, Philominathan P (2012) Composite dynamical behaviors in a simple series-parallel LC circuit. Chaos Solitons Fractals 45:1501–1509

    Article  Google Scholar 

  49. Bier M, Bountis TC (1984) Remerging Feigenbaum trees in dynamical systems. Phys Lett A 104:239–244

    Article  MathSciNet  Google Scholar 

  50. Yujun N, Xingyuan W, Mingjun W, Huaguang Z (2010) A new hyperchaotic system and its circuit implementation. Commun Nonlinear Sci Numer Simul 15:3518–3524

    Article  Google Scholar 

  51. Jafari A, Mliki E, Akgul A, Pham VT, Kingni ST, Wang X, Jafari S (2017) Chameleon: the most hidden chaotic flow. Nonlinear Dyn. doi:10.1007/s11071-017-3378-4

  52. Kingni ST, Nana B, Mbouna Ngueuteu GS, Woafo P, Danckaert J (2015) Bursting oscillations in a 3D system with asymmetrically distributed equilibria: mechanism, electronic implementation and fractional derivation effect. Chaos Solitons Fractals 71:29–40

    Article  MATH  MathSciNet  Google Scholar 

  53. Pham VT, Volos C, Jafari S, Sundarapandian V, Kapitaniak T, Wang X (2016) A chaotic system with different families of hidden attractors. Int J Bifurc Chaos 26(8):1650139

    Article  MATH  MathSciNet  Google Scholar 

  54. Elsonbaty AR, El-Sayed AMA (2016) Further nonlinear dynamical analysis of simple jerk system with multiple attractors. Nonlinear Dyn 87(2):1169–1186

    Article  MATH  Google Scholar 

  55. Hamil DC (1991) Learning about chaotic circuits with SPICE. IEEE Trans Ed 36(1):28–35

    Article  Google Scholar 

  56. Kengne J, Njitacke Tabekoueng Z, Fotsin HB (2016) Coexistence of multiple attractors and crisis route to chaos in autonomous third order Duffing–Holmes type chaotic oscillators. Commun Nonlinear Sci Numer Simul 36:29–44

    Article  MathSciNet  Google Scholar 

  57. Bianchi G, Kuznetsov NV, Leonov GA, Seledzhi SM, Yuldashev MV, Yuldashev RV (2016) Hidden oscillations in SPICE simulation of two-phase Costas loop with non-linear VCO. IFAC Pap OnLine 49(14):45–50

    Article  Google Scholar 

  58. Kamdoum Tamba V, Fotsin HB, Kengne J, Megam Ngouonkadi EB, Talla PK (2016) Emergence of complex dynamical behaviors in improved Colpitts oscillators: antimonotonicity, coexisting attractors, and metastable chaos. Int J Dyn Control. doi:10.1007/s40435-016-0223-4

Download references

Author information

Authors and Affiliations

  1. Laboratoire d’Automatique et Informatique Appliquée (LAIA), Department of Electrical Engineering, IUT-FV Bandjoun, University of Dschang, Dschang, Cameroon

    Jacques Kengne, V. R. Folifack Signing & G. D. Leutcho

  2. Laboratory of Electronics and Signal Processing, Department of Physics, University of Dschang, P.O. Box 67, Dschang, Cameroon

    V. R. Folifack Signing & G. D. Leutcho

  3. Institute of Smart Systems Technologies, University of Klagenfurt, Klagenfurt, Austria

    J. C. Chedjou

Authors
  1. Jacques Kengne
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. V. R. Folifack Signing
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. J. C. Chedjou
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. G. D. Leutcho
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jacques Kengne.

Electronic supplementary material

Below is the link to the electronic supplementary material.

Supplementary material 1 (pdf 6 KB)

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Kengne, J., Signing, V.R.F., Chedjou, J.C. et al. Nonlinear behavior of a novel chaotic jerk system: antimonotonicity, crises, and multiple coexisting attractors. Int. J. Dynam. Control 6, 468–485 (2018). https://doi.org/10.1007/s40435-017-0318-6

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40435-017-0318-6

Keywords

Search

Navigation