Abstract
Application of the MEBDFV code in multibody dynamics is discussed. The solver is based on the modified extended backward differentiation formulae of Cash. It is especially suited for the solution of differential-algebraic equations with time- and state-dependent mass matrix. Such a case can occur when motion of a multibody open-chain system is described within the classical Lagrangian formalism, which still has some advantages. An outline of the numerical algorithm is given. As an example, a simplified mathematical model of the human head-cervical spine system is presented. In a numerical experiment the model is used to analyze motion of the head–neck during rear-end impact which may lead to whiplash injury. The obtained results are compared to literature data. Performance of the MEBDFV solver is examined in terms of algorithmic energy conservation. The test is based on an appropriately formulated ‘kinetic energy–work’ relation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Multibody dynamics is one of the most rapidly developing branches of computational mechanics. The specific area is strictly based on well-known concepts of classical and analytical mechanics such as D’Alembert’s principle, Newton–Euler equations, Lagrangian formalism, etc. As an extension of these approaches some generalized methodologies for formulating dynamic equations have appeared over the past few decades. These modern techniques are especially suitable for computer implementation and can be applied to a vast class of multibody systems. In general there are two basic formulations which are widely used: the embedding techniques and the augmented formulation [1, 2]. Both of them have adavantages and disadvantages related to computational issues like number of equations, their nonlinearity and complexity. Usually the techniques involve applying the free body principle in order to obtain the equations of motion.
However, in some cases purely analytical methods seem to be preferable. The typical examples are conventional and inverted multiple pendula which over the last few decades have been the subject of theoretical and experimental studies mainly from the viewpoint of nonlinear dynamics and control theory (see e.g. [3–10]). In general, multibody systems with a chain topology are especially likely to be modelled via the standard Lagrangian formulation. Basically, by the term ‘standard formulation’ the authors mean applying the Lagrange’s equations of the second kind, where all the generalized coordinates are independent and the dynamic equations do not involve constraint forces, e.g. the ones which act at the joints connecting rigid members. In such a case the standard approach can be regarded as an embedding technique. However, if some additional geometric constraints are imposed on the system (for instance, the other end of the chain is fixed), the former equations of motion are still useful. In the method of Lagrange multipliers, for example, the primary model can be extended by introducing constraints equations and undetermined multipliers which are related just to the new reaction forces [11, 12]. This procedure, in turn, corresponds to the augmented formulation.
There are some advantages of the standard approach to the open-chain systems. Firstly, minimal or almost minimal (if the additional constraints exist) set of coordinates is used to describe a system. Moreover, the internal (connection) forces are not included in the dynamic equations. Both the factors reduce the problem dimensionality. Secondly, the equations of motion can be derived from a few scalar quantities specific for a certain system: the kinetic energy, potential energy and dissipation function. This feature is crucial especially when dealing with a system of bodies interconnected by many coupling elements like springs, dampers and actuators.
Nevertheless, there is one significant drawback of the discussed approach: high complexity of the dynamic equations. It can be regarded as the well-known side effect of the selection of a small number of coordinates [1]. In case of the open-chain systems, when the small vibrations assumption is not made, the mathematical model is given by the set of implicit differential equations (IDEs):
where \(\mathbf{q}\) is the vector of generalized coordinates. Clearly, the left-hand side matrix \(\mathbf{M}\) (usually called the mass matrix) is indirectly time-dependent, for it depends on the generalized coordinates explicitly. Numerical solving of the problem may be a cumbersome task, particularly for mechanical systems with many degrees of freedom. Indeed, the basic, widely known numerical methods are designed for ODEs in the normal (explicit) form [13, 14]. Using them for time integration of the system (1) requires inversion of the non-constant matrix \(\mathbf{M}\), which is numerically expensive.
Although rarely described, among commonly available IVP solvers there are a few which are suited for solving IDEs [15]. In this paper the code MEBDFV designed by T.J. Abdulla and J.R. Cash is employed. We discuss its application to computer simulation of the open-chain multibody systems. In particular, we consider a simplified mathematical model of the human head-cervical spine system. The aim of this paper is to show that equations of motion in the implicit form can be solved satisfactorily and the standard Lagrangian approach, readily used in the field of theoretical mechanics, is not doomed to failure.
2 The MEBDFV code for multibody dynamics problems
2.1 General form of dynamic equations and a numerical model
Assume that equations of motion of a given multibody system have the implicit form (1). For numerical integration they are rearranged and written as
where
In the above formulae \(\mathbf{I}\) denotes an identity matrix and \(\mathbf{u}=\dot{\mathbf{q}}\) is the vector of generalized velocities. To find a unique solution to the dynamic equations, a set of initial conditions has to be defined. Using the state vector \(\mathbf{X}\) associated to positions and velocities of the rigid bodies, one canwrite
If additional geometric constraints are imposed on the mechanical system
a full description of its dynamics is given by
where
and \(\varvec{\lambda }\) is the vector of undetermined Lagrange multipliers. In the simplest, straightforward way the resulting system of differential-algebraic equations (DAEs) can be written as in (2) but the matrices have the augmented form:
In such a case the initial conditions (4) refer to the multipliers \(\varvec{\lambda }\) too.
2.2 The origins of the modified extended BDF
As can be seen, the system of IDEs (3) is a special case of DAEs (8). Nevertheless, the problems that involve both differential and algebraic equations are more demanding numerically. Similar to the case of stiff systems of ODEs, methods used for DAEs have to satisfy rigorous stability requirements. Other difficulties are related to error estimation and convergence, which enforces more sophisticated strategies in comparison to the methods intended for standard ODEs [16].
Generally, complexity of a problem increases with an index of DAEs, \(i_D\). For example, DAEs (6) are of index 3 for most constrained multibody systems; in the case of ODEs (\({\hat{\mathbf{M}}} = \mathbf{I}\)) and IDEs (\({\hat{\mathbf{M}}} \ne \mathbf{I}\) and \(\det ({\hat{\mathbf{M}}}) \ne 0\)), in turn, \(i_D = 0\). For more details on the concept of DAEs index the reader is referred to [17, 18].
Majority of the codes originated in the 1980’s and 1990’s have been restricted to \(i_D \le 3\) (e.g. DASSL, LSODI, GAMD). Therefore, many methods have been developed to reduce the problem index, e.g. the GGL formulation, the Baumgarte’s technique [18]. Today there are several solvers commonly used for the solution of DAEs of higher index. However, not all of them are suited to the DAE systems with non-constant mass matrix (2) or the unstructured ones (e.g. BiMD or RADAU5) [15].
The MEBDFV solver is suitable for the numerical solution of DAEs with index \(i_D \le 3\), given in the form (2). The code is based on the modified extended backward differentition formulae (MEBDF) of Cash. In 80’s the researcher proposed a separate class of numerical methods, clearly different from both the standard backward differentition formulae (BDF) and the widely used Runge–Kutta (RK) type methods [19, 20]. The new approach resulted in very efficient schemes with extremely good stability properties. Thus, the MEBDF formulae can be regarded as a third path, aside (i) linear multistep methods, which are cheap to implement but, due to the famous Dahlquist’s barrier, at higher orders have pure stability, and (ii) implicit Runge–Kutta methods with potentially excellent stability but expensive implementation. The origins of the new approach were described by Cash [21].
Like other codes based on MEBDF, designed for initial value problems in ODEs and DAEs of various forms, the MEBDFV solver is available on the Internet [22]. As usual, the code contains a brief description of input and output parameters as well as the subroutines which must be supplied by a user. Needless to say, the information does not give a detailed insight into mechanisms of the numerical integration.
Treated as fundamentals of numerical methods for differential equations, the BDF and RK formulae have been discussed in many books, e.g. [13, 14, 23–25]. The MEBDF approach, in turn, has not become commonly known as yet. Moreover, issues related to IDEs or DAEs are covered in literature very rarely. Taking into account their importance to computational dynamics and capabilities of the MEBDFV solver, we feel that the MEBDF approach in application to DAEs of the form (2) merits further attention.
2.3 MEBDFV from the inside
This section does not contain a deep analysis of implementation details of the MEBDF. From practical point of view, however, it is important to generally understand computational ideas associated with the code MEBDFV, which prevents from using it in a black-box manner.
Assume that approximate solutions \(\mathbf{X}_1,\, \mathbf{X}_2,\, \ldots ,\, \mathbf{X}_{i-1}\) have been computed at the corresponding step points \(t_1, t_2,\, \ldots ,\, t_{i-1}\). The key idea of the MEBDF approach is to find \(\mathbf{X}_{i}\) by using not only the previous values of \(\mathbf{X}\) and \(\dot{\mathbf{X}}\), but also their approximations at the superfuture point \(t_{i+1}\).
For convenience sake, let us write the fully implicit form of DAE system (2):
where
Furthermore, in the formulae used below \(\widetilde{\mathbf{w}}\) denotes an initial approximation (prediction) of a given vector function \(\mathbf{w}\), whereas \(\mathbf{w}^{*}\) is the value corrected due to an iterative process; \(h\) denotes the current stepsize. Now, an outline of the computational algorithm can be given in a form of the following three stages:
-
1.
First BDF step
Given the predicted value \(\widetilde{\mathbf{X}}_{i}\), use a standard \(k\)-step BDF to evaluate the derivative approximation \(\widetilde{\dot{\mathbf{X}}}_{i}\):
$$\begin{aligned} \widetilde{\mathbf{X}}_{i} + \sum _{j=1}^{k} \alpha _j \mathbf{X}_{i-j} = h \beta _0 \widetilde{\dot{\mathbf{X}}}_{i}\,. \end{aligned}$$(11)Note that \(\widetilde{\dot{\mathbf{X}}}_{i}\) is expressed in terms of \(\widetilde{\mathbf{X}}_{i}\), thus, now (9) becomes a nonlinear algebraic system where \(\mathbf{X}_{i}\) is the only unknown. Find an approximate solution \(\mathbf{X}_{i}^{*}\) and use formula (11) to recompute the derivative, i.e. to obtain \(\dot{\mathbf{X}}_{i}^{*}\).
-
2.
Second BDF step
Predict the superfuture value \(\widetilde{\mathbf{X}}_{i+1}\) and use the same BDF as before, but go one step further, i.e. evaluate \(\widetilde{\dot{\mathbf{X}}}_{i+1}\):
$$\begin{aligned} \widetilde{\mathbf{X}}_{i+1} + \alpha _{1} \mathbf{X}_{i}^{*} + \sum _{j=1}^{k-1} \alpha _j \mathbf{X}_{i-j} = h \beta _0 \widetilde{\dot{\mathbf{X}}}_{i+1}\,. \end{aligned}$$(12)Insert \(\widetilde{\mathbf{X}}_{i+1}\) and \(\widetilde{\dot{\mathbf{X}}}_{i+1}\) to (9) and find \(\mathbf{X}_{i+1}^{*}\). Use formula (12) again to compute a new value \(\dot{\mathbf{X}}_{i+1}^{*}\).
-
3.
MEBDF step
Use both \(\mathbf{X}_{i}^{*}\), \(\dot{\mathbf{X}}_{i}^{*}\) and \(\mathbf{X}_{i+1}^{*}\), \(\dot{\mathbf{X}}_{i+1}^{*}\) to compute a corrected derivative \(\dot{\mathbf{X}}_{i}\) according to the modified extended BDF:
$$\begin{aligned}&\mathbf{X}_{i}^{*} + \sum _{j=1}^{k} \bar{\alpha }_j \mathbf{X}_{i-j}\nonumber \\&\quad = h \left[ \bar{\beta }_1 \dot{\mathbf{X}}_{i+1}^{*} + \beta _0 \dot{\mathbf{X}}_{i} + (\bar{\beta }_0 - \beta _0) \dot{\mathbf{X}}_{i}^{*} \right] \,. \end{aligned}$$(13)One more time solve the system of nonlinear equations (9). The found solution \(\mathbf{X}_{i}\) is the final result of the time integration process.
It can be proven that, although the conventional BDF (11) and (12) have order \(k\), the scheme (13) is of order \((k+1)\) [19]. All the coefficients \(\alpha _j\), \(\beta _j\), \(\bar{\alpha }_j\), \(\bar{\beta }_j\) are listed in papers [19, 20]. Some computational aspects of the outlined stages require further explanation.
Firstly, it should be noted that a fully adaptive algorithm is implemented inside MEBDFV: time stepsize \(h\) as well as order \(k\) are adjusted automatically. The user, however, can specify the minimal stepsize and the maximal order. Changes in \(h\) slightly complicate managing the past data involved in the schemes. Normally, MEBDFV uses the history array based on backward differences:
where
If \(h\) is changed (e.g. after unsuccessful computation), the history array is rescaled appropriately [20, 26].
When considering the three stages, estimation of the initial approximations may seem troublesome. However, given the history array, the prediction is straightforward:
where \(\mathbf{H}_{i-1,j}\) denotes the \(j\)th item of \(\mathbf{H}_{i-1}\). In fact, this formula is applied mainly for stage (2). If \(h\) has not been changed, stage (1) can use the corrected superfuture value \(\mathbf{X}_{i+1}^{*}\) from stage (2) of the previous time step. Stage (3), in turn, naturally starts with the solution \(\mathbf{X}_{i}^{*}\) corrected at stage (1) of the current step.
It is the solution of the nonlinear algebraic system which is crucial to the overall computational effort. Let us consider Eq. (9) in case of the first stage. After using the BDF, derivative \(\dot{\mathbf{X}}_{i}\) is regarded as a function of \(\mathbf{X}_{i}\) and the resulting nonlinear set of equations takes the form
As with many solvers based on implicit formulae, the code MEBDFV implements the modified Newton method. Thus, the iteration scheme can be written as
The correction \(\varvec{\delta }_{i}\) is obtained by solving the linear algebraic system
where \(\mathbf{J}\) is the Jacobian matrix:
If \({\hat{\mathbf{F}}}\) has the form (10), the matrix is given by
For the whole iterative process the vector \(\widetilde{\mathbf{X}}_{i}\) plays a role of the start point:
Scheme (17) is iterated to convergence. Consequently, successive approximations \(\mathbf{X}_{i}^{(p)}\) for \(p=1,\, 2,\, \ldots ,\, N\) are generated and eventually \(\mathbf{X}_{i}^{*} = \mathbf{X}_{i}^{(N)}\). Analogous procedure is performed at the stages (2) and (3).
It should be emphasized that \(\mathbf{J}\) is kept fixed for all \(N\) iterations. What is more, a specific construction of the method allows to use the same Jacobian matrix at each of the stages (1–3). It considerably reduces the computational effort related to evaluation and factorization of \(\mathbf{J}\). In addition, the first and third stages are usually provided with excellent approximations as mentioned before. Therefore, only a few iterations are needed to reach convergence [20, 26].
The discussed implementation of MEBDF goes even further. Indeed, Abdulla and Cash adopted the strategy of updating the Jacobian matrix only when it is indispensable. Thus, an old matrix \(\mathbf{J}\) is used for many time steps, as long as no ‘ill effects’ arise. If convergence is not achieved, for example, the Jacobian is re-evaluated and Newton iterations are retried; if still computation fails, the stepsize is halved [20, 26].
Of course, the code MEBDFV employs numerous other techniques and strategies related to such issues as: selecting optimal stepsize, maintaining good convergence of the Newton scheme, estimating the convergence rate, controlling local errors, etc. Nevertheless, these aspects refer to detailed numerical analysis, which goes beyond the overview necessary to comprehend main concepts of the MEBDF implementation.
At the end of this section it is worth noting that, basically, the user supplies the routines which compute the matrix \({\hat{\mathbf{M}}}\) (banded or full), the right-hand side vector \({\hat{\mathbf{F}}}\) and \(\mathbf{J}\) (banded or full). If the matrix of partial derivatives \(\mathbf{J}\) is to be evaluated numerically, a routine computing the residual delta \({\hat{\mathbf{F}}}\) should be specified instead.
3 Biomechanical system and equations of motion
3.1 Human cervical spine and its models
The cervical spine consists of seven vertebrae (denoted by C1–C7); each of them has different shape and geometric parameters. The main role of this spine column is to carry the weight of a head and ensure its appropriate mobility. For every vertebra (excluding C1), a vertebral body is the part responsible for carrying load resulting from muscles and the head. Between adjacent vertebral bodies (excluding C1–C2) there is an intervertebral disc which, thanks to its flexibility, stabilizes them and responds to compressive forces. Additionally, unproper mobility of the particular parts is restricted by ligaments which couple the adjacent vertebrae [27, 28].
Since it is difficult to precisely describe mechanical properties of bone tissue and soft tissues, one can find various mechanical models of certain segments of the spine. One of the earliest models of the head/neck system based on multibody dynamics was proposed by Deng and Goldsmith [29]. The authors modeled vertebrae as rigid bodies and included intervertebral connections, muscles and ligaments with nonlinear characteristics. They studied dynamics of the system during road accidents. Dauvilliersa et al. [30] proposed a model with linear charactristics of ligaments and elastic, isotrophic intervertebral discs. De Jager et al. [31, 32] developed the model of Deng and Goldsmith by assumption that the head and vertebrae are rigid members but discs are represented through viscoelastic joints with nonlinear characteristics determined experimentally. Yang et al. [33] analyzed motion of the cervical spine in sagittal plane leading to spinal injuries. In this model both elastic and viscoelastic nature of the ligaments was considered. Van der Horst [34] extended the de Jager’s model by describing the discs and ligaments as viscoelastic nonlinear elements. Van Lopik and Acar [35] presented a three-dimensional multibody model of the head and neck for the analysis of whiplash motion. Apart from the discs and ligaments they took into account facet joints too.
In many classical models of the human spine, different approaches to modeling of bone tissue and soft tissue were used. In study of the cervical spine dynamics usually vertebrae are treated as rigid bodies. Where it comes to ligaments, one can find numerous models. The simpliest way to reflect the ligaments character is to assume that they are two- [36] or three-dimensional [37] linear elements. In more advanced approaches the ligaments were considered to be linear elastic elements with the same value of Poisson’s ratio and diverse stiffness coefficient [38]. Dauvillers et al. [30], in turn, modeled the ligaments as linearly elastic elements with damping and used identical stiffness constant for all of them. Some authors proposed nonlinear models [39–41]. Due to common use of the finite element method in numerical simulations, shell and beam models [33] as well as the spring and axial (link) ones [42] have become popular.
Similar to the ligaments, the intervertebral discs are described in diverse manner. In problems related to cervical spine biomechanics, solid models are widely applied. It is assumed that a disc is a homogenuous elastic body with known Young’s modulus and Poisson’s ratio [38, 39, 43]. In order to take into account the acting loads, the discs were divided into three parts: annulus, annulus fibrosus and nucleus pulposus. In [33, 37] authors proposed discs comprised of two bodies representing the annulus and nucleus. Goel et al. [44] additionally applied a beam model for the annulus fibrosus. In turn, de Jager et al. [40] used viscoelastic linear elements to represent the annulus and nucleus. Kumeresan et al. [42] employed a solid model of the annulus, beam model of the annulus fibrosus; the nucleus was treated as incompressible liquid. In the model of van Lopik and Acar [35] the discs were represented by non-linear viscoelastic ‘bushing’ constraints.
3.2 Multibody model of cervical spine
It is not the purpose of this section to present a novel and complete (in some measure) model of the cervical spine. Actually, the multibody system discussed below has a two-dimensional, simplified nature. However, despite its limited complexity, the model is a good example of application of the standard Lagrangian approach leading to a system of IDEs.
Consider the head–neck system. The presented model is based on the following assumptions:
-
For the sake of simplicity, analysis is restricted to plane motion of the system, i.e. its motion in the midsagittal plane.
-
The head (H) and seven vertebrae (C1–C7) are treated as rigid bodies connected by joints.
-
The torso (with the Th1 vertebra of the thoracic spine) plays a role of a base for the system.
-
The ligaments are represented by elastic-dissipative elements of known characteristics.
-
Effect of musculature on the system motion is neglected.
-
Geometric and inertial properties of the members as well as attachement points of the elastic-dissipative elements are given.
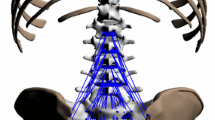
Figure 1 shows a physical model of the biomechanical system. Naturally, the rigid members are interconnected via joints, however, their character is assumed to be non-ideal. Since we do not directly include the intervertebral discs in the model, we use nonlinear spring-damper elements of rotational nature located in the joints. Additionally, couplings between particular vertebrae are reflected by Kelvin–Voight spring-damper elements. They can be regarded as a model of the anterior longitudinal ligaments and the interspinous ones. In the same way connections at H-C1 and C7-Th1 are introduced too. Although the upper cervical spine differs in structure from the lower segment (e.g. the atlas (C1) does not have a body and the atlanto-axial joints (C1–C2) are more complex [27]), all the vertebrae are treated uniformly.
In mathematical description of the system we apply indexing of the members which is reverse to the numbers of vertebrae. Namely, the C7 vertebra has index \(i=1\), while \(i=8\) for the head. Now, consider a simple representation of the \(i\)th body. As can be seen in Fig. 2, there are several characteristic points selected: the pivot \(O_i\), the mass center \(S_i\), the posterior and arterior attachement points for the spring-damper elements denoted by \(A'_i\), \(A''_i\) and \(B'_i\), \(B''_i\), respectively. In a local coordinate system position of an arbitrary point \(P\) associated to the \(i\)th member can be specified by values \(\Delta x_{P}\) and \(\Delta y_{P}\) (positive or negative). Similarly, \(\Delta x_{i}\) and \(\Delta y_{i}\) determine position of \(O_{i+1}\) with respect to \(O_i\).
The discussed mechanical system has \(n=8\) degrees of freedom and the angular variables \(\varphi _i\), \(i=1,\, 2,\, \ldots ,\, n\) can serve as the generalized coordinates (see Fig. 3). For the sake of generality, assume that the base point \(O_1\) can move and its position is given by the explicit functions of time:
Positions of the pivots \(O_i\) in the global Cartesian system can be expressed in terms of the generalized coordinates:
Now, global coordinates of the point \(P\) belonging to the \(i\)th member can be written as
Particularly, coordinates of the mass centers \(S_i\) are given by
Kinetic energy of the system has the following form:
where \(v_{Si}\) is velocity of the \(i\)th mass center:
while \(m_i\) denotes mass of the member and \(I_{Si}\) is its moment of inertia with respect to \(S_i\). Potential energy, in turn, can be specified as
Each of the above components are briefly described below:
-
\(U_i^G\) is the gravitational potential energy of the \(i\)th member:
$$\begin{aligned} U_i^G = m_i g y_{Si} \end{aligned}$$(29) -
\(U_{Ai}^S\) is the potential energy of the spring that connects points \(A''_{i-1}\) and \(A'_i\):
$$\begin{aligned} U_{Ai}^S = \frac{1}{2} k_{Ai} \xi _{Ai}^2\,, \end{aligned}$$(30)where \(k_{Ai}\) denotes the stiffness coefficient of the spring and \(\xi _{Ai}\) is the distance between \(A''_{i-1}\) and \(A'_i\):
$$\begin{aligned} \xi _{Ai} = \sqrt{(x_{A'i} - x_{A''i-1})^2 + (y_{A'i} - y_{A''i-1})^2} \end{aligned}$$(31) -
\(U_{Bi}^S\) is the potential energy of the spring that connects points \(B''_{i-1}\) and \(B'_i\):
$$\begin{aligned} U_{Bi}^S = \frac{1}{2} k_{Bi} \xi _{Bi}^2\,, \end{aligned}$$(32)where \(k_{Bi}\) denotes the stiffness coefficient of the spring and \(\xi _{Bi}\) is the distance between \(B''_{i-1}\) and \(B'_i\):
$$\begin{aligned} \xi _{Bi} = \sqrt{(x_{B'i} - x_{B''i-1})^2 + (y_{B'i} - y_{B''i-1})^2} \end{aligned}$$(33) -
\(U_{Oi}^S\) is the potential energy of the torsional spring located in the pivot \(O_{i}\). Much information on determining stiffness of the intervertebral joints of the upper and lower cervical spine was presented by de Jager [32], who derived strongly nonlinear load-displacement curves from experimental data. Therefore, instead of defining the energy \(U_{Oi}^S\), we postulate the generalized elastic forces
$$\begin{aligned} Q_{Oi}^S = - \frac{\partial U_{Oi}^S}{\partial \varphi _i} \end{aligned}$$in the following form [8]:
$$\begin{aligned} Q_{Oi}^S = \left\{ \begin{array}{l@{\quad }l@{\quad }l} - M_{Oi} + M_{Oi+1} &{} \quad \text {if}\;\; &{} i = 1,\, 2,\, \ldots ,\, n-1 \\ - M_{Oi} &{} \quad \text {if}\;\; &{} i = n \end{array} \right. \end{aligned}$$(34)where
$$\begin{aligned} M_{Oi} = k_{Oi} \frac{\tan (\theta _i/2)}{\cos (\theta _i/2)} \end{aligned}$$(35)is the elastic moment arising in \(i\)th joint; \(k_{Oi}\) denotes the stiffness coefficient of the spring and \(\theta _i\) is the relative angular coordinate given by
$$\begin{aligned} \theta _i = \left\{ \begin{array}{l@{\quad }l@{\quad }l} \varphi _i &{} \quad \text {if}\;\; &{} i=1 \\ \varphi _i-\varphi _{i-1} &{} \quad \text {if}\;\; &{} i=2,\, 3,\, \ldots ,\, n \end{array} \right. \end{aligned}$$(36)The resulting characteristics of the intervertebral joints is shown in Fig. 4.
Using the formula (24), one can express the Cartesian coordinates of \(A''_{i-1}\), \(A'_i\), \(B''_{i-1}\), \(B'_i\) in terms of the generalized coordinates. Note that the points \(A''_0\) and \(B''_0\) are located at the base of the system (the Th1 vertebra), whereas \(A'_8\) and \(B'_8\) belong to the head.
To mathematically describe damping effects, let us introduce the Rayleigh’s dissipation function:
By analogy to \(U_{Ai}^S\) and \(U_{Bi}^S\), all the components of \(R\) are specified in a quadratic manner:
where \(c_{Ai}\), \(c_{Bi}\), \(c_{Oi}\) denote the damping coefficients of the particular dissipative elements and \(\dot{\xi }_{Ai}\), \(\dot{\xi }_{Bi}\), \(\dot{\theta }_{i}\) are velocities of their deformation.
Equations of motion for the system can be derived from the Lagrange equations of the second kind:
On the right-hand side the following terms are considered:
-
the generalized potential force \(Q_i^{p}\) given by
$$\begin{aligned} Q_i^{p} = - \frac{\partial U}{\partial \varphi _i}\,, \end{aligned}$$(40)which has the two basic components:
$$\begin{aligned} Q_i^{p} = Q_i^{G} + Q_i^{S}\,, \end{aligned}$$(41)where \(Q_i^{G}\) results from gravity and \(Q_i^{S}\) is the generalized elastic force including the term (34)
-
the generalized nonpotential force \(Q_i^{np}\) which is a sum of the two components: the dissipative force
$$\begin{aligned} Q_i^{R} = - \frac{\partial R}{\partial \dot{\varphi }_i} \end{aligned}$$(42)and a generalized external force \(Q_i^{\text {ext}}\) applied to the member
After determining all the derivatives of \(T\), \(U\) and \(R\) which appear in Eq. (39), the dynamic equations of the system take the form:
The quantities \(a_{ij}\) and \(a'_{ij}\) are functions of the generalized coordinates:
where
and
In turn, the function \(\gamma \) is given by
where
Ultimately, the generalized forces are determined as
where the following functions are introduced:
and the constants can be written as
The same relations involving points \(B'_i\) and \(B''_{i-1}\) can be specified simply by replacing \(A\) with \(B\) in formulae (45) and (46).
As can be seen, the equations of motion (43) can be rearranged and presented in the matrix form (1), where
and the matrix \(\mathbf{M}\) consists of the coefficients \(a_{ij}\).
4 Numerical experiment
In order to present numerical perfomance of the MEBDFV code in dynamic simulations based on the discussed model, whiplash motion of the head–neck system is analyzed. The term ‘whiplash’ is related to one of the most frequent cervical spine injuries which occur mainly in automobile accidents and lead to significaant societal costs. Such an injury results from a sudden, excessive movement of the head with respect to torso, which produces soft tissue damage in the neck. Despite lots of various hypotheses, there is no definitive explanation of the mechanisms leading to the whiplash trauma. Dynamics of the head–neck system during impacts is still studied both experimentally and computationally [35, 45].
Although whiplash motion can be generated in all impact configurations, usually it is a consequence of rear-end collisions. Panjabi and co-workers [45, 46] used isolated cervical spine specimens and a bench-top sled apparatus to perform rear-impact simulation. The base of a specimen was subject to horizontal acceleration of 3.5, 5, 6.5 and 8\(g\). The phenomenon was analyzed numerically by van Lopik and Acar [35] who studied peak accelerations of 2.5, 4.5, 6.5 and 8.5\(g\).
Let the acceleration profile have the form of a triangular pulse, lasting \(t_2=105\;\text {ms}\) with a peak value \(a_{\max }=8.5g\) at \(t_1=t_2/2\) (see Fig. 5a). To realize such a kinematic excitation of the system, the following Th1 horizontal translation should be assumed (see Fig. 5b):
For purposes of our simulations geometric data for planar models of vertebrae is taken from a radiograph of a healthy volunteer. As illustrated in Fig. 6, shape representation of every body is based on eight characteristic points. Similar to the models described in [46, 47], the center of mass is positioned at the center of the segment connecting the corners \(P_1\) and \(P_6\) of the vertebral body. It is assumed that point \(P_5\) of the \(i\)th member and \(P_2\) of the next one are coupled by a link rigidly connected with the lower body, and the pivot \(O_{i+1}\) is located in the point \(P_2\). Points \(P_3\), \(P_4\), \(P_7\), \(P_8\) correspond to the ligaments attachment points: \(B''\), \(B'\), \(A'\) and \(A''\), respectively. The center of mass of the head is located near the sella turcica. However, geometric representation of the skull is used mainly for visual purposes. Inertial properties of the vertebrae and head are adapted from [32, 47]. Values of the elastic-dissipative parameters have been selected by trial and error. For simplicity, the stiffness and damping coefficients are supposed to be uniform along the cervical spine (see Table 1).
Initial configuration of the system \(\mathbf{q}(0)\) is specified according to the radiograph. Generalized velocities, in turn, are set to zero: \(\dot{\mathbf{q}}(0) = \mathbf{0}\).
Figure 7 displays time history of the head–neck response to \(8.5g\) rear-end impact (\(g=9.81\; \text {m/s}^2\)). The results are very similar to the ones reported in [35]. Head translations in the global coordinate system and head velocity are presented in Fig. 8 against the background of the imposed excitation. As can be seen, in the nonzero acceleration interval the head is displaced posteriorly and inferiorly. This motion corresponds to a gradual development of spinal extension. However, the numerical and experimental results indicated that initially just the lower levels of the spine are extended while the upper levels are subjected to flexion [35, 45]. It leads to a specific S-shape curvature of the spine. At the later stage of the whiplash the whole cervical spine becomes extended and a C-shape curvature is formed. Such an effect can be observed in the current simulation too. Figure 9 shows graphs of ligaments forces caused by the impact, i.e. the forces exerted on the rigid bodies by the spring-damper elements. The quantities are calculated by taking changes of the couplers lengths:
The negative values related to the anterior ligaments at C1–C2, C2–C3 and C3–C4 as well as the positive forces in the interspinous ligaments at the same levels indicate slight flexion of the upper spine segment. Transition from S- to C-shape phase occurs over the 50–75 ms time period, earlier than in the experiments [45]. On the other hand, maximum extension of the head–neck system arises near \(t=140\) ms, that is too soon when compared to the results reported in [35, 45]. The peak force value is approximately equal to 45 N (C4–C5). It is worth noting that average values of the force at failure for the mentioned ligaments vary from 26 to 207 N depending on spinal level [48]. Additionally, there are considerable deviations of the forces resulting from individual differences.
Obviously, better agreement between the simulation and the results presented by other authors requires more complete head–neck model and its validation. Nevertheless, the aim goes beyond the scope of this paper.
From the computational point of view, performance of the solver is essential. It can be examined in many ways, not only by measuring CPU time related to numerical integration of dynamical equations. In case of mechanical systems, the test criterion can be based naturally on the so-called algorithmic energy conservation. It is commonly known that in simulation the given system may artificially gain or loose energy due to numerical inaccuracy. Very often the energy decreases which is referred to as ‘numerical dissipation’. The problem appears in dynamics of rigid bodies and multibody systems modeled via various approaches, even if a set of DAEs with a constant mass matrix is obtained. Hence, many researchers apply certain formulations and/or design specific time integration schemes, which leads to good conservation properties of the resulting algorithm [49–52].
If the analyzed system is conservative, the solver assessment is straightforward: relates to theoretically constant total energy \(E = T+U\). In the given example, however, \(E\) fluctuates (see Fig. 10). It is not only because of the damping, but also due to the kinematic excitation. Unlike the former one, the latter factor entails energy growth. In such a case, the energy-based test should employ more complicated physical principle. One of the applicable methods is described below.
As it is known the kinetic energy of mechanical systems can always be defined as the sum of three functions [12, 53]:
where \(T_0\) is independent on the generalized velocities, \(T_1\) depends on them linearly, and \(T_2\) is a homogeneous quadratic form of the generalized velocities. Only if the system is scleronomic, \(T_0\) and \(T_1\) vanish, and the system is called ‘natural’. The term \(T_2\) is referred to as ‘relative kinetic energy’ [54]. Indeed, if the system is rheonomic, \(T_2\) represents the kinetic energy with respect to the moving (non-inertial) reference frame fixed to the system.
Generally, the given multibody model is rheonomic because the transformation Eqs. (25) and (23) involve time explicitly via \(x_{O1}(t)\) and \(y_{O1}(t)\). The two functions are a source of the term \(\gamma _i\), included in the equations of motion (43) and strictly connected to \(T_0\) and \(T_1\). The additional quantity sets up the \(i\)th ‘transport inertia force’ arising from the imposed motion of the base (the torso) and reference frame (\(x_{1}O_{1}y_{1}\)) [54]:
Now, the ‘kinetic energy–work’ principle may be formulated as follows [7]:
Here, \(\Delta T_2\) denotes a change of the relative kinetic energy produced by the work \(W\) done by all forces, including \(Q_{i}^{*}\):
where \(\mathcal {S}\) is the configuration path of the dynamical system. Considering that \(T_2(0) = 0\), the relation (51) can be rewritten in the form
where
Hence, one can define a relative error as
where \(T_{2\max }\) denotes the maximal value of \(T_2\) in the given time interval.
A graph of the error in the time interval \(0 \le t \le 5\) s is presented in Fig. 11. As can be seen, \(e_R\) fluctuates and stabilizes in response to vibration decay and stabilization of the entire mechanical system. The maximal value is equal to 0.0103. Presumably, it is an effect of the triangular acceleration impulse and the rapid velocity change imposed on the system’s base. Of course, using the formula (54) requires numerical integration of the generalized forces. The results have been obtained by applying the extended trapezoidal rule for \(\Delta t = 5\times 10^{-5}\) s. No significant differences are noticed after reducing the stepsize.
5 Conclusions
In this paper we have discussed application of the MEBDFV solver to dynamic simulation of multibody systems. The code is particularly useful for open-chain systems modeled via the classical Lagrangian formulation, since such an approach leads to a set of implicit differential equations or DAEs with non-constant mass-matrix. The most important concepts of the numerical algorithm have been outlined. As it has been shown, the solver does not use the explicit form of DAEs, thus, when the imposed constraints require the use of Lagrange multipliers, singularity of the mass matrix does not constitute any numerical problem.
As an example, a two-dimensional multibody model of the cervical spine has been considered. The proposed system includes bone tissue, intervertebral discs and selected ligaments. The equations of motion have been derived in the framework of the Lagrangian formalism. This approach allows to take into account various models of interactions between spinal vertebrae and skull. Also kinematical excitation of the system may be considered. Consequently, one can deal with some important biomechanical problems like the whiplash trauma. In the numerical experiment we have especially focused on the ligaments forces and their values at failure. Although the presented model is incomplete and its validation has not been conducted, the obtained results are qualitatively similar to the ones reported in other works.
Moreover, the MEBDFV solver performance has been evaluated in terms of the algorithmic energy conservation. Since the system is subjected to rheonomic constraints, the ‘kinetic energy–work’ relation has been applied in an appropriate form, including the relative kinetic energy and the transport inertia forces. The numerical experiment indicates that the solver provides satisfactory results, with low energy inconsistency. Furthermore, it can be easily checked that in case of different test problems the computation process is time-efficient compared to well-known, two-dimensional dynamic simulation environments such as Working Model 2D.
References
Shabana A (2010) Computational Dynamics, 3rd edn. Wiley, New York
Shabana A (2005) Dynamics of Multibody Systems, 3rd edn. Cambridge University, Cambridge
Awrejcewicz J, Kudra G, Lamarque C (2004) Investigation of triple pendulum with impacts using fundamental solution matrices. Int J Bifurcat Chaos 14(12):4191–4213
Awrejcewicz J, Kudra G (2005) Stability analysis and Lyapunov exponents of a multi-body mechanical system with rigid unilateral constraints. Nonlinear Anal 63:e909–e918
Lobas L (2005) Generalized mathematical model of an inverted multilink pendulum with follower force. Int Appl Mech 41(5): 566–572
Galán J, Fraserb W, Achesonc D, Champneysd A (2005) The parametrically excited upside-down rod: an elastic jointed pendulum model. J Sound Vibr 280:359–377
Fritzkowski P, Kamiński H (2009) Dynamics of a rope modeled as a discrete system with extensible members. Comput Mech 44(4):473–480
Fritzkowski P, Kamiński H (2011) A discrete model of a rope with bending stiffness or viscous damping. Acta Mech Sin 27(1):108–113
Bendersky S, Sandler B (2006) Investigation of a spatial double pendulum: an engineering approach. Discrete Dyn Nat Soc 2006: 1–22
Plaut R, Virgin L (2013) Pendulum models of ponytail motion during walking and running. J Sound Vibr 332:3768–3780
Hand LN, Finch JD (1998) Analytical Mechanics. Cambridge University, Cambridge
Thornton S, Marion J (2004) Classical Dynamics of Particles and Systems, 5th edn. Brooks/Cole, New York
Press W, Teukolsky S, Vetterling W, Flannery B (2007) Numerical Recipes: The Art of Scientific Computing, 3rd edn. Cambridge University, Cambridge
Hoffman J (2001) Numerical Methods for Engineers and Scientists, 2nd edn. Marcel Dekker Inc., New York
Mazzia F, Magherini C (2008) Test set for initial value problem solvers. Tech. Rep. 4/2008, Department of Mathematics, University of Bari, Italy. http://www.dm.uniba.it/~testset/testsetivpsolvers/
Petzold L (1982) Differential/Algebraic Equations are not ODE’s. SIAM J Sci Stat Comput 3(3):367–384
Riaza R (2008) Differential-Algebraic Systems: Analytical Aspects and Circuit Applications. World Scientific, Singapore
Costa-Castelló R, Griñó R, Basañez L (1998) DAE methods in constrained robotics system simulation. Computatión y Sistemas 1(3):145–160
Cash J (1980) On the integration of stiff systems of ODEs using extended backward differentiation formulae. Numer Math 34(3):235–246
Cash J (1983) The integration of stiff initial value problems in ODEs using modified extended backward differentiation formulae. Comp Math Appl 9(5):645–657
Cash J (2000) Modifed extended backward differentiation formulae for the numerical solution of stiff initial value problems in ODEs and DAEs. J Comput Appl Math 125:117–130
Cash J (2000) Software for initial value problems. http://www2.imperial.ac.uk/~jcash/IVP_software/readme.php
Conte S, de Boor C (1980) Elementary Numerical Analysis: An Algorithmic Approach, 3rd edn. McGraw-Hill, New York
Stoer J, Bulirsch R (1991) Introduction to Numerical Analysis, 2nd edn. Springer, New York
Shampine L, Allen RC (1997) Fundamentals of Numerical Computing. Wiley, New York
Cash J, Considine S (1992) An MEBDF code for stiff initial value problems. ACM T Math Softw 18(2):142–155
Middleditch A, Oliver J (2002) Functional Anatomy of the Spine. Butterworth–Heinemann, Oxford
de Jager M (1993) Mathematical modelling of the human cervical spine: A survey of the literature. Tech. Rep. WFW-93.027, Faculty of Mechanical Engineering Eindhoven University of Technology, The Netherlands
Deng Y, Goldsmith W (1987) Response of a human head/ neck/upper-torso replica to dynamic loading - II. Analytical/numerical model. J Biomech 20:487–491
Dauvilliers F, Tarriere C, Lavaste F, Weiss M, Bendjellal F (1994) Development of finite element method of the neck. In: Proceedings of 38th Stapp Car Crash Conference, pp 77–91
de Jager M, Sauren A, Thunnissen J, Wismans J (1996) A global and detailed mathematical model for head–neck dynamics. In: Proceedings of 40th Stapp Car Crash Conference, pp 269–281
de Jager M (1996) Mathematical head–neck models for acceleration impacts. Ph.D. thesis, University of Eindhoven
Yang K, Zhu F, Luan F, Zhao L, Begeman P (1998) Development of a finite element model of the human neck. In: Proceedings of 42nd Stapp Car Crash Conference, pp 195–205
Horst MVD (2002) Human head neck response in frontal, lateral and rear end impact loading: modelling and validation. Ph.D. Thesis, Eindhoven University of Technology
van Lopik D, Acar M (2004) A computational model of the human head and neck system for the analysis of whiplash motion. Int J Crashworthiness 9(1):465–473
Saito T, Yamamuro T, Shikata J, Oka M, Tsutsumi S (1991) Analysis and prevention of spinal column deformity following cervical laminectomy, pathogenetic analysis of post laminectomy deformities. Spine 16(5):494–502
Yoganandan N, Kumaresan S, Voo L, Pintar F (1996) Finite element application in human cervical spine modeling. Spine 21(15): 1824–1834
Kleinberger M (1993) Application of finite element techniques to the study of cervical spine mechanisms. In: Proceedings of 37th Stapp Car Crash Conference, pp 261–272
Williams J, Bellytschko T (1983) A three-dimensional model of the human cervical spine for impact simulations. J Biomech Eng 105(4):321–331
de Jager M, Sauren A, Thunnissen J, Wismans J (1994) A three dimensional head-neck model: validation for frontal and lateral impacts. In: Proceedings of 38th Stapp Car Crash Conference, pp 93–109
Stemper B, Yoganandan N, Pintar F (2004) Validation of a headneck computer model for whiplash simulation. Med Biol Eng Comput 42(3):333–338
Kumaresan S, Yoganandan N, Pintar F (1997) Pediatric neck modeling using finite element analysis. Int J Crashworthiness 2(4): 367–376
Nitsche S, Krabbel G, Appel H, Haug E (1996) Validation of a finite element model of the human neck. In: Proceedings of International Conference of Biomechanics of Impact, pp 107–108
Goel V, Scifert J, Grosland N Finite element investigation of anterior plate and bone graft load sharing in the cervical spine. Tech. rep., Departments of Biomechanical Engineering and Orthopaedic Surgery, University of Iowa, Iowa City
Panjabi M, Pearson A, Ito S, Ivancic P, Wang J (2004) Cervical spine curvature during simulated whiplash. Clin Biomech 19(1): 1–9
Ivancic P, Panjabi M, Ito S (2006) Cervical spine loads and intervertebral motions during whiplash. Traffic Inj Prev 7(4):389–399
van Lopik D, Acar M (2007) Development of a multi-body computational model of human head and neck. Proc Inst Mech Eng 221:175–197
Myklebush J, Pintar F, Yoganandan N, Cusick J, Maiman D, Myers T, Sances A (1988) Tensile strength of spinal ligaments. Spine 13(5):526–531
Cohen D, Hairer E, Lubich C (2005) Numerical energy conservation for multi-frequency oscillatory differential equations. BIT Numer Math 45(2):287–305
Betsch P, Leyendecker S (2006) The discrete null space method for the energy consistent integration of constrained mechanical systems. Int J Numer Meth Eng 67:499–552
Uhlar S, Betsch T (2009) Energy-consistent integration of multibody systems with friction. J Mech Sci Tech 23(4):901–909
Nielsen M, Krenk S (2012) Conservative integration of rigid body motion by quaternion parameters with implicit constraints. Int J Numer Meth Eng 92(5):734–752
Goldstein H, Poole C, Safko J (2001) Classical Mechanics, 3rd edn. Addison Wesley, San Francisco
Gürgöze M (2006) On the formulation of Lagrange’s equations with respect to moving coordinate systems: application to a point mass vibrating on a rotating base. Int J Mech Eng Edu 34(3): 263–272
Acknowledgments
This work has been supported by 21-387/2011 DS-MK and 21-407/2012 DS-MK Grants. It is an extension of an earlier paper presented during 12th Conference on Dynamical Systems: Theory and Applications (DSTA 2013).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Fritzkowski, P., Walczak, T. Application of the MEBDFV solver to dynamic simulation of some specific multibody systems: an example of a cervical spine model. Int. J. Dynam. Control 3, 17–30 (2015). https://doi.org/10.1007/s40435-014-0076-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40435-014-0076-7