1 Introduction

In the engineering applications, the damping property of the structure is an important factor to be considered in suppression of the harmful vibration. The approach of adding damping can be mainly divided into three categories: passive vibration control, semi-active vibration control and active vibration control. Compared with the active control, the semi-active and the passive vibration control using passive energy-dissipation materials or devices have many advantages, for instance, no requirement or only little requirement of energy input, absolute stable, no need of sensors and power amplifiers, simple implementation, etc. Therefore, semi-active and passive vibration controls are still the main methods to enhance damping in the engineering structures, though various active control methods have emerged.

Piezoelectric shunt damping is a kind of passive technique to suppress the vibration of structures [1]. In this method the mechanical energy of the vibrating structure is converted into electrical energy and dissipated by the resistance in the shunt circuit. Piezoelectric shunt damping is also classified as a semi-active method because some kinds of shunt circuit energy is needed to synthesize impedance [2] or switch shunt [3]. In this paper the classification criterion [4] is used: an electrical shunt is said to be passive if it does not supply energy to the structure. Various kinds of piezoelectric shunt damping methods have been proposed in the last two decades. In resistance shunt method [1], the energy cannot be fully dissipated due to the reactive power of the capacitance in the piezoelectric transducer. To cancel the reactive power of the capacitance resonant shunt method [1] and negative capacitance shunt method [2] were developed. Recently, switch shunt method [3] was proposed in order to overcome some drawbacks in classical shunts, like the need of large inductance and the sensitivity to the shunt resonance frequency.

Resonant shunt can be seen as a vibration absorber mathematically. So the values of inductance and resistance in each shunt must be optimized. Preument et al. [5] provided the optimal RL value based on root locus plot while Thomas et al. [6] used pole placement criterion. But in these methods the structure was treated as one degree of freedom systems based on modal truncation. In this paper it will be shown that when the number of mechanical degree of freedom (DOF) is far more than the electrical DOF, the optimal RL value based on modal truncation can lose effectiveness and must be further tuned. So a practical search method will be proposed in this paper based on eigenvalue analysis.

There are some works to realize multimode or broadband vibration control by designing various kinds of shunts. Wu [7] used current blocking branches in shunt circuit to dissipate multi-frequency energy, while Hollkamp [8] employed parallel RLC shunts. Similar methods can also be seen in [9, 10]. In these methods only one complex shunt circuit was used. To realize frequency selection of different modes, large number of capacitances and inductances were employed, and analysis of these circuits became difficult task. Alessandroni et al. [11] utilized both distributed piezoelectric transducers and distribute electric networks to obtain broadband damping character. Casadei et al. [12] provided a method using independent periodic arrays of piezoelectric patches and circuits to reduce vibration of a plate in a wide frequency bond based on the wave propagation theory. Trindade and Maio [13] employed independent shear piezoelectric materials connected to independent resistive shunt circuits to control multimode vibration of a beam. The method in this paper is similar to the above method, except that an approach will be developed to make the piezoelectric transducers and resonant shunts more independent. Compared with other multimode shunt methods, the advantages of the present method are that: (1) to use fewer inductances and no excess capacitances; (2) to be more reliable due to the independence of the modal transducers and modal shunts, that is, if one transducer or shunt fails to work, the damping character of other modal will not be seriously affected; (3) to control more modes easily by adding additional modal shunts and no need for the retuning of the existing shunts. This is reason that the present method is named as “independent modal resonant shunt for vibration control”.

Similar to piezoelectric shunt, viscoelastic material [14] is also a traditional passive damping-enhancing method in mechanical structures. The performance of shunt damping and viscoelastic damping are seldom compared in the existing research works. In this paper it will be demonstrated that the mathematical models of resonant shunt damping and viscoelastic damping are the same. Both of them can be seen as a vibration absorber. But the “mass” and “damping” of the resonant shunt are respectively inductance and resistance and can be tuned in order to get the best performance, while the parameters of viscoelastic damper are determined by the material parameters and can not be changed after its manufacture. So the resonant shunt damping has advantage over the viscoelastic damping.

The aim of this study is to apply the proposed independent modal resonant shunt for the multimode vibration control of a truss-cored sandwich panel? called Kagome structure. Attentions are also paid to the optimization of RL values in the shunt and comparison between resonant shunt damping and viscoelastic damping. This paper is organized as follows: In Sect. 2 the introduction of the Kagome structure and the finite element model of the electromechanical structure is presented. In Sect. 3, the independent modal resonant shunt method is detailed and the optimal value of RL is studied. In Sect. 4, the validity and the advantages of this method is demonstrated through the time-domain simulation on the responses of the Kagome structure. Resonant shunt damping and viscoelastic damping are compared in Sect. 5. Finally, conclusions are drawn in Sect. 6.

2 Finite element model of Kagome structure with resonant shunt

2.1 Kagome structure

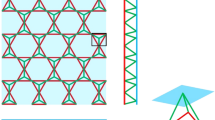
The Kagome structure [15] consists of a solid face sheet and a tetrahedral core and a planar Kagome truss as the back-plane (see Fig. 1). While some rods in the planar truss are replaced by in-plane tension- compression actuators, the transverse displacement of its solid face sheet of this structure can be realized by the in-plane tension-compression of the actuators.

Fig. 1
figure 1

Schematic representation of the Kagome structure. The solid face sheet is shown in dark grey, the core in grey and the planar Kagome truss as one face plane in black [19]

Full size image

A traditional approach to passively suppress vibration of plate-like structure is using constrained layer damping [16] while active vibration control is often realized by bonding piezoelectric patch [17] to the surface. However, these kinds of control methods are at the expense of adding considerable weight to the structure while the surface of the plate will be changed. The morphing character of Kagome structure can be taken use for passive/active controls. The idea is to replace a very small portion of the rods only in the planar Kagome truss by dampers [18] to dissipate energy or by actuator [19] to generate control forces in order to suppress the vibration of the Kagome structure subjected to the out-of-plane excitation. In this paper, the rods in the planar truss will be replaced by piezoelectric transducer to convert the mechanical energy to electric energy which is dissipated by the shunt.

The material and parameters of the Kagome structure are listed in Table 1. There are totally 546 truss rods in the planer Kagome truss. The boundary condition is clamped-clamped.

Table 1 Material parameters and size of face sheet and truss rods
Full size table

The finite element model of the Kagome structure built by NASTRAN is shown in Fig. 2. The face sheet is discretized using 414 plate elements CQUAD4, while the 1110 truss-cores and planar Kagome truss are modeled by simple beam elements CBAR. The first six modal shapes were calculated by MSC.NASTRAN as shown in Fig. 3

Fig. 2
figure 2

a Finite element model of Kagome structure. The arrow represents the loaded point of structure response in Sect. 4, b The back plane of the Kagome structure with a planar Kagome truss

Full size image
Fig. 3
figure 3

Mode shapes 1–6 with modal frequencies 297, 507, 550, 717, 775, 836 Hz, respectively

Full size image

2.2 Electromechanical structure

The rod-like piezoelectric transducer is adopted (see Fig. 4a) to replace small number of rods in the planar Kagome of the Kagome structure. The transducer is mainly composed of a piezoelectric stack, outer casing, preloading spring and two link rods. A sphere joint is used to prevent the piezoelectric stack from bending and torsion moments. Each transducer is connected to a resonant shunt with a resistance and an inductance in it (see Fig. 4b).

Fig. 4
figure 4

Sketch of a the piezoelectric actuator, b electro-mechanical structure

Full size image

To build the finite element model of the electromechanical structure, first the condition using one transducer and one shunt is considered. The kinetic coenergy of the structure is:

$$\begin{aligned} T^{*}=\frac{1}{2}\left\{ {\dot{x}} \right\} ^{T}\left[ M \right] _{\mathrm{s}} \left\{ {\dot{x}} \right\} \end{aligned}$$
(1)

where \([M]_{\mathrm{s}}\) represents the mass matrix of Kagome structure coupled with piezoelectric transducer and \(\{x\}\) is the displacement vector of the nodes.

The magnetic coenergy of the inductance is

$$\begin{aligned} W_{\mathrm{m}}^*=\frac{1}{2}L\dot{q}^{2} \end{aligned}$$
(2)

where \(L\) represents value of inductance and \(q\) is the electric charge of the shunt.

The strain energy of the structure is:

$$\begin{aligned} V=\frac{1}{2}\left\{ x \right\} ^{T}\left[ K \right] _{\mathrm{s}} \left\{ x \right\} \end{aligned}$$
(3)

where \([K]_{\mathrm{s}}\) represents the stiffness matrix of the mechanical part.

The electromechanical energy of the transducer is:

$$\begin{aligned} W_{\mathrm{e}} =\frac{1}{2C\left( {1-k^{2}} \right) }q^{2}+\frac{nd_{33} K_{\mathrm{a}} }{C\left( {1-k^{2}} \right) }q\left\{ b \right\} ^{T}\left\{ x \right\} \end{aligned}$$
(4)

where \(C\) is unloaded capacitance of the piezoelectric stack which includes \(n\) disks, \(K_{a}\) is the short-circuited electrode stiffness of piezoelectric transducer, \(k\) is the electromechanical coupling factor, \(d_{33}\) is the piezoelectric constant and {\(b\)} is position vector of the transducer. The parameters of the stack transducer can be found in [5].

The Lagrangian of the system can be written as [5]:

$$\begin{aligned} \mathcal{L}=T^{{*}}+W_{\mathrm{m}}^{*} -W_{\mathrm{e}} -V \end{aligned}$$
(5)

Neglecting damping of the structure, define the dissipation function \(P\) which represents the energy dissipation of the resistance \(R\) as:

$$\begin{aligned} P=\frac{1}{2}R\dot{q}^{2} \end{aligned}$$
(6)

The second-kind Lagrange equation takes the form as:

$$\begin{aligned} \frac{d}{dt}\left( {\frac{\partial \mathcal{L}}{\partial \dot{u}_i }} \right) -\frac{\partial \mathcal{L}}{\partial u_i }+\frac{\partial P}{\partial \dot{u}_i }=0 \end{aligned}$$
(7)

where \(u_{i}\) is the \(i\)th generalized coordinate. The dynamic equation of the electromechanical system can be obtained as:

$$\begin{aligned}&\left[ M \right] _{\mathrm{s}} \left\{ {\ddot{x}} \right\} +\left[ K \right] _{\mathrm{s}} \left\{ x \right\} -\frac{\left\{ b \right\} nd_{33} K_{\mathrm{a}} }{C\left( {1-k^{2}} \right) }q=0 \nonumber \\&L\ddot{q}+R\dot{q}+\frac{1}{C\left( {1-k^{2}} \right) }q+\frac{nd_{33} K_{\mathrm{a}} }{C\left( {1-k^{2}} \right) }\left\{ b \right\} ^{T}\left\{ x \right\} =0 \end{aligned}$$
(8)

Equation (8) can be written in matrix form:

$$\begin{aligned} \left[ M \right] \left\{ {\ddot{u}} \right\} +\left[ D \right] \left\{ {\dot{u}} \right\} +\left[ K \right] \left\{ u \right\} =\left\{ 0 \right\} \end{aligned}$$

where:

$$\begin{aligned} \left[ M \right]&= \left[ {{\begin{array}{ll} {\left[ M \right] _{\mathrm{s}}}&{} \\ &{}\quad L \\ \end{array}}} \right] \qquad \left[ D \right] =\left[ {{\begin{array}{ll} {\left[ 0 \right] }&{} \\ &{}\quad R \\ \end{array}}} \right] \nonumber \\ \left[ K \right]&= \left[ {{\begin{array}{ll} {\left[ K \right] _{\mathrm{s}} }&{}\quad {\frac{nd_{33} K_{\mathrm{a}} }{C\left( {1-k^{2}} \right) }\left\{ b \right\} } \\ {\frac{nd_{33} K_{\mathrm{a}}}{C\left( {1-k^{2}} \right) }\left\{ b \right\} ^{T}}&{}\quad {\frac{1}{C\left( {1-k^{2}} \right) }} \\ \end{array}}} \right] \nonumber \\ \left\{ u \right\}&= \left\{ {{\begin{array}{ll} {\left\{ x \right\} }&{} q \\ \end{array} }} \right\} ^{T} \end{aligned}$$
(9)

While there are \(n\) transducers which share the same character and \(n\) resonant shunts with different RL values, the matrices in Eq. (9) are:

$$\begin{aligned} \left[ M \right]&= \left[ {{\begin{array}{llll} {\left[ M \right] _{\mathrm{s}} }&{} &{} &{} \\ &{} {L_1 }&{} &{} \\ &{} &{} \ddots &{} \\ &{} &{} &{} {L_n } \\ \end{array} }} \right] ,\qquad \left[ D \right] =\left[ {{\begin{array}{llll} {[0]}&{} &{} &{} \\ &{} {R_1 }&{} &{} \\ &{} &{} \ddots &{} \\ &{} &{} &{} {R_n } \\ \end{array} }} \right] ,\nonumber \\ \left[ K \right]&= \left[ {{\begin{array}{llll} {\left[ K \right] _{\mathrm{s}} }&{}\quad {\frac{nd_{33} K_{\mathrm{a}} }{C\left( {1-k^{2}} \right) }\left\{ b \right\} _1 }&{}\quad \cdots &{} \quad {\frac{nd_{33} K_{\mathrm{a}} }{C\left( {1-k^{2}} \right) }\left\{ b \right\} _n } \\ {\frac{nd_{33} K_{\mathrm{a}} }{C\left( {1-k^{2}} \right) }\left\{ b \right\} _1^T }&{}\quad {\frac{1}{C\left( {1-k^{2}} \right) }}&{}\quad \cdots &{}\quad 0 \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ {\frac{nd_{33} K_{\mathrm{a}} }{C\left( {1-k^{2}} \right) }\left\{ b \right\} _n^T }&{}\quad 0&{}\quad \cdots &{}\quad {\frac{1}{C\left( {1-k^{2}} \right) }} \\ \end{array}}} \right] \nonumber \\ \left\{ u \right\}&= \left\{ {\left\{ x \right\} }\quad {q_1 }\quad \cdots \quad {q_n} \right\} ^{T} \end{aligned}$$
(10)

3 Multimode independent modal resonant shunt vibration control method

3.1 Principles of independent modal resonant shunt vibration control method

In independent modal resonant shunt vibration control method, there is a two-step frequency-selecting process of vibration energy: For each mode, first, a piezoelectric transducer (called modal transducer) is allocated to mainly transform vibration energy of this mode into electric energy. Then a resonant shunt (called modal shunt) is connected to this modal transducer to mainly dissipate the electric energy of this mode. The second step is more strict and plays the major role due to the fine frequency-selecting property of RLC resonant circuit. Because of this frequency-selecting process, each modal transducer with modal shunt is independent, and adding or removing modal transducer with modal shunt do not affect the damping character of other modes. The flow chart of this method is shown in Fig. 5 to illustrate the energy dissipation procession of mode \(i\).

Fig. 5
figure 5

Flow chart of energy dissipation procession of mode \(i\)

Full size image

To realize the first frequency-selecting process, the location of the modal transducer must be optimized to transform the energy of this mode into electric energy as more as possible. And to realize the second frequency-selecting process, the RL values of the modal shunt also must be optimized to tune the frequency of the circuit close to the corresponding mechanical modal frequency to add the most damping to the corresponding mechanical mode. These problems will be studied below.

3.2 Optimization of the modal transducer location

Consider only the \(i\)th mechanical mode (mode of Kagome structure without shunt), Eq. (8) is truncated as:

$$\begin{aligned}&\ddot{x}_i +\omega _{{\mathrm{o}}i} x_i -\frac{nd_{33} K_a }{C\left( {1-k^{2}} \right) }\lambda _i q=0 \nonumber \\&L\ddot{q}+R\dot{q}+\frac{1}{C\left( {1-k^{2}} \right) }q+\frac{nd_{33} K_a }{C\left( {1-k^{2}} \right) }\lambda _i x_i =0 \end{aligned}$$
(11)

where \(x_{i }\) is coordinate of the \(i\)th mode,\(\omega _{\mathrm{o}i}\) is open-electrode circle frequency of the \(i\)th mode with open-electrode transducer stiffness:

$$\begin{aligned} K_{\mathrm{ao}} =\frac{K_{\mathrm{a}} }{1-k^{2}} \end{aligned}$$
(12)

and \(\lambda _{i}\) is defined as:

$$\begin{aligned} \lambda _i =\left\{ b \right\} ^{T}\left\{ {\varphi _i } \right\} =\left\{ {\varphi _i } \right\} ^{T}\left\{ b \right\} \end{aligned}$$
(13)

where \(\{\varphi _{i}\}\) represents modal shape vector of the \(i\)th mode of the mechanical structure. Obviously, \(\lambda _{i}\) reflects the coupling strength of piezoelectric transducer with the \(i\)th mode. So for mode \(i\), the modal transducer must be located to the position with maximal \(\lambda _{i}\). Because the number of piezoelectric used in this method equals the number of mode to be controlled, there is only a small part of rod in Kagome planar truss will be replaced by transducer so it can be supposed that \(\lambda _{i}\) will not change after transducer is allocated. So, for mode \(i,\,\lambda _{i}\) of every Kagome planar rod will be calculated and the one with the largest \(\lambda _{i}\) will be replaced by the modal transducer.

In fact, there is relation between \(\lambda _{\mathrm{i}}\) with modal strain energy (MSE) of mode \(i\). MSE of mode \(i\) can be calculated as:

$$\begin{aligned} \nu _i =\frac{1}{2}K_{\mathrm{a}} \left\{ {\varphi _i } \right\} ^{T}\left\{ b \right\} \left\{ b \right\} ^{T}\left\{ {\varphi _i } \right\} =\frac{1}{2}K_{\mathrm{a}} \lambda _i^2 \end{aligned}$$
(14)

Because \(K_{a}\) is constant among all transducers, the traditional MSE method can also be used to determine the optimal position of the modal transducer.

In this paper, modes 1–3 are considered to be controlled, so three piezoelectric transducers are needed. Through calculation of \(\lambda _{i}\), the locations of transducers can be decided as in Fig. 6.

Fig. 6
figure 6

Locations of modal transducers of modes 1–3. The number 1–3 represents the mode to be controlled by each transducer

Full size image

3.3 Optimization of the modal shunts

There have been several methods to optimize the RL value of the resonant shunt based on single mode coupled with the resonant shunt. It was indicated in [6] that the damping added by shunt does not depend on the structural damping, so the structural damping will still be neglected. According to [5] the optimal RL values in the shunt of mode \(i\) are:

$$\begin{aligned} L_{i{\mathrm{opt}}}&= \frac{\omega _{{\mathrm{s}}i}^2 }{\omega _{{\mathrm{o}}i}^4 C\left( {1-k^{2}} \right) } \nonumber \\ R_{i{\mathrm{opt}}}&= \frac{2\omega _{{\mathrm{s}}i} }{\omega _{{\mathrm{o}}i}^2 C\left( {1-k^{2}} \right) }\sqrt{\frac{k^{2}\delta _i }{1-k^{2}}} \end{aligned}$$
(15)

where \(\omega _{si}\) is circle frequency of the \(i\)th mode with short-circuited electrode of the transducer. And

$$\begin{aligned} \delta _i =\frac{\nu _i }{\frac{1}{2}\omega _{{\mathrm{s}}i}^2 } \end{aligned}$$
(16)

is the fraction of MSE of the transducer in the structure which vibrating according to mode \(i\). Through Eq. (15), the optimal RL values for mode 1–3 can be calculated: \(L_{1}=3.18\, {H},\,R_{1}=643\,\Omega ,\,L_{2}=1.1\, {H},\,R_{2}=417\,\Omega , L_{3}=0.93\, {H}, R_{3}=345\,\Omega \). Substituting these values into Eq. (10) with \(n=3\), the complex eigenvalues of the electromechanical structure can be obtained composed with 1884 mechanical modes and 3 electrical modes contributed by the shunt. In Table 2 the first three mechanical modes and all three electrical modes are listed:

Table 2 The first three mechanical modes and all three electrical modes of the full model
Full size table

Because damping of the structure is neglected, the computed damping ratios of mechanical modes are the additional damping ratios contributed by the shunts. It can be seen that while the electrical modes possess large damping ratios devoted by \(R\), the increment of mechanical damping ratio is very small. Further, frequency of each electrical mode is not closed to its corresponding mechanical mode. So the poor damping performance is due to the badly tuned RL values.

When only considering the first three modes of the structure coupling with three modal shunts, the eignevalues are calculated and the first three mechanical modes and all three electrical modes are listed in Table 3. Obviously, when truncating the mechanical modes into only three modes, the RL values obtained by Eq. (15) perform well. In fact, the electromechanical structure is a complex mode system, if the number of mechanical DOF is far more than electrical DOF, the order-reducing method which first truncating the mechanical DOF then coupling the reduced structure model with the shunts can be invalid. The small number of electrical modes can be affected by the large number of mechanical modes, while the former influents little on the latter.

Table 3 The first three mechanical modes and all three electrical modes of the truncated model
Full size table

In [5] it was pointed out that the shunts get the optimal tuning when the eigenvalue of electrical mode coincides with its corresponding mechanical mode. So the RL values obtained by Eq. (15) must be further optimized to make the damping ratios and frequencies of an electrical mode as near as possible to its corresponding mechanical mode. In \(n\) modal shunts there are \(n\) inductances and \(n\) resistances, so the optimization problem is 2\(n\)-dimensional. But in this paper it is found that after the frequency of one electrical mode is tuned close to its corresponding mechanical mode through changing \(L\), change of \(R\) brings only a small influence on the tuned frequency. And, if one modal shunt has been tuned successfully, when tuning other shunt, the influence on this tuned mode is very little due to the frequency-selecting character of the resonant shunt. So the \(2n\)-dimensional optimization problem can be reduced to \(2n\) one-dimensional problems while each can be resolved by a simple heuristic search method.

In this multimode modal shunt optimization method, the modal shunts are tuned one by one, and for each modal shunt, first calculate the eigenvalue with RL value given by Eq. (15) using the full model of electromechanical structure. Then search an \(L\) value to make the frequency close to the mechanical frequency to some extent by calculating the eigenvalues. Here the difference of mechanical and electrical frequency will be controlled in 5 \(L\) is well tuned, the optimal \(R\) value is searched to make the damping ratio of mechanical mode maximal. If RL values of one mode are optimized, move to the next mode.

To illustrate the advantages of this optimization method, the optimization of RL values in modal shunt 1–3 will be executed and demonstrated step-by-step. In the following text, \(f_{\mathrm{i}}\) and \(\xi _{\mathrm{i}}\) represent frequency of the \(i\)th electrical mode and damping ratio of the \(i\)th mechanical mode, respectively.

  1. (1)

    After \(L_{1}\) is tuned, \(f_{1}=295\, {Hz}\).

  2. (2)

    After \(R_{1}\) is tuned, \(f_{1}=292\, {Hz}, \xi _{1}=0.029\).

  3. (3)

    After \(L_{2}\) is tuned, \(f_{1}=292\, {Hz}, \xi _{1}=0.029, f_{2}=507\, {Hz}\).

  4. (4)

    After \(R_{2}\) is tuned, \(f_{1}=292\, {Hz}, \xi _{1}=0.029, f_{2}=504\, {Hz}, \xi _{2}=0.023\).

  5. (5)

    After\(L_{3}\) is tuned, \(f_{1}=292\, {Hz}, \xi _{1}=0.029, f_{2}=504\, {Hz}, \xi _{2}=0.023, f_{3}=547\, {Hz}\).

  6. (6)

    After \(R_{3}\) is tuned, \(f_{1}=292\, {Hz}, \xi _{1}=0.029, f_{2}=504\, {Hz}, \xi _{2}=0.024, f_{3}=546\, {Hz}, \xi _{3}=0.021\).

It can be seen that the six parameters of the three modal shunts can be optimized one-by-one and the optimized parameters need not be retuned when tuning other parameters. Finally, the optimal values of inductances and resistances are: \(L_{1}=2.34\, {H},\,R_{1}=515\,\Omega ,\,L_{2}=0.8\, {H},\,R_{2}=266\,\Omega ,\,L_{3}=0.64\, {H},\,R_{3}=204\,\Omega \). And the corresponding eigenvalues are listed in Table 4. It can be seen that the damping ratios of the mechanical modes are raised remarkably.

Table 4 The first three mechanical modes and all three electrical modes with the optimal resonant shunts
Full size table

Besides calculating the eigenvalues based on finite element model, this optimization method can also be using experimental modal analysis in which the mechanical eigenvalues can be obtained by testing the structure while the electrical eigenvalues can be got by testing the shunt circuit. So the optimization method proposed in this paper is not only simple but also practical.

4 Time-domain simulation

In this section, time-domain response of Kagome structure is simulated to validate the efficiency of independent modal resonant shunt control for multimode. The Rayleigh damping model is applied to the structure so the damping matrix can be written as:

$$\begin{aligned} \left[ D \right] _{\mathrm{s}} =\alpha \left[ M \right] _{\mathrm{s}} +\beta \left[ K \right] _{\mathrm{s}} \end{aligned}$$
(17)

where \(\alpha =23.5\) and \(\beta =3.96\times 10^{-6}\) to set the modal damping ratios of mode 1–2 at 1 %. And the damping matrix of the electromechanical structure can be written as:

$$\begin{aligned} \left[ D \right] =\left[ {{\begin{array}{llll} {[D]_{\mathrm{s}} }&{} &{} &{} \\ &{} {R_1 }&{} &{} \\ &{} &{} \ddots &{} \\ &{} &{} &{} {R_n } \\ \end{array} }} \right] \end{aligned}$$
(18)

For the structure with and without control, an 1000 N impulse force acts on the point shown in Fig. 2 and the response of the same point is plotted in Fig. 7. The time history shows that with independent modal resonant shunt control of modes 1–3, the free response decays more quickly. And spectrum of the responses drawn in Fig. 7b illustrates that the first three resonant peaks decreased significantly, while the other peaks are not changed due to the frequency-selecting character of this method.

Fig. 7
figure 7

a The time history of response under the impulse excitation of the structure without control and with mode 1–3 controlled, b spectra of responses

Full size image

To verify the independence between different modal shunts, first remove shunt of the second mode and calculate spectrum of the responses. Figure 8 shows that after removing the second mode shunt, the second resonant peak does not decrease any more while the others peaks decrease or remain unchanged as in Fig. 7b. Next, a fourth modal shunt is added to control the vibration of mode 4 with its location shown in Fig. 9. The parameters of this modal shunt are optimized as: \(L=0.37\, {H},\,R=146\,\Omega \). The control result is illustrated in Fig. 10. Obviously, significant damping is added to mode 4 while the other modes keep invariant. So removing or adding a modal shunt will only affect damping character of this mode while the other mode will not be affected.

Fig. 8
figure 8

Spectra of responses of the structure without control and with mode 1 and 3 controlled

Full size image
Fig. 9
figure 9

Locations of modal transducers of mode 1–4. The number 1–4 represents the mode to be controlled by each transducer

Full size image
Fig. 10
figure 10

Spectra of responses of the structure without control and with mode 1–4 controlled

Full size image

5 Comparison of resonant shunt and viscoelastic damping

A traditional and widely-used passive vibration control method is using viscoelastic damper. In this section, resonant shunt damping and viscoelastic damping will be compared by the mathematic model and effect.

Considering a kind of bi-shearing viscoelastic damper [18] composed of a core rod, a sleeve and viscoelastic material (see Fig. 11). When the relative movement between the core rod and the sleeve undergoes, the viscoelastic material will undertake shearing deformation and dissipate energy. Spherical hinges are used in the connection between the damper and the Kagome truss members to prevent bending and torsion.

Fig. 11
figure 11

Sketch of the bi-shearing viscoelastic damper

Full size image

Suppose \(n\) rods in Kagome truss are replaced by the dampers using the same kind of viscoelastic material. Employing Golla–Hughes–McTavish (GHM) model of viscoelastic material with one mini-oscillator term [16], the finite element model of the viscoelastic-elastic composed structure can be written as:

$$\begin{aligned} \left[ M \right] \left\{ {\ddot{u}} \right\} +\left[ D \right] \left\{ {\dot{u}} \right\} +\left[ K \right] \left\{ u \right\} =\left\{ 0 \right\} \end{aligned}$$

where:

$$\begin{aligned} \left[ M \right]&= \left[ {{\begin{array}{llll} {\left[ M \right] _{\mathrm{s}}}&{} &{} &{} \\ &{} {2\gamma G^{\infty }\frac{\alpha }{\omega _v^2 }}&{} &{} \\ &{} &{} \ddots &{} \\ &{} &{} &{} {2\gamma G^{\infty }\frac{\alpha }{\omega _v^2 }} \\ \end{array} }} \right] \nonumber \\ \left[ D \right]&= \left[ {{\begin{array}{llll} {[0]}&{} &{} &{} \\ &{} {4cG^{\infty }\frac{\alpha \xi _v }{\omega _v }}&{} &{} \\ &{} &{} \ddots &{} \\ &{} &{} &{} {4cG^{\infty }\frac{\alpha \xi _v }{\omega _v }} \\ \end{array} }} \right] \nonumber \\ \left[ K \right]&= \left[ {{\begin{array}{llll} {\left[ K \right] _{\mathrm{s}} }&{} {\sqrt{2}\alpha _1 \left\{ b \right\} _1 }&{} \cdots &{} {\sqrt{2}\alpha _n \left\{ b \right\} _n } \\ {\sqrt{2}\alpha _1 \left\{ b \right\} _1^T }&{} {2\gamma G^{\infty }\alpha }&{} \cdots &{} 0 \\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ {\sqrt{2}\alpha _n \left\{ b \right\} _n^T }&{} 0&{} \cdots &{} {2\gamma G^{\infty }\alpha } \\ \end{array} }} \right] \nonumber \\ \left\{ u \right\}&= \left\{ {\left\{ x \right\} } {z_1 } \cdots {z_n } \right\} ^{T} \end{aligned}$$
(19)

Here \([M]_{\mathrm{s}},\,[K]_{\mathrm{s}}\) are mass and stiffness matrix of the elastic part of the viscoelastic-elastic composed structure while the damping of the elastic part is neglected. \(G^{\infty },\alpha ,\omega _{v},\xi _{v }\) are parameters depending on the viscoelastic material. \(z_{i}\) (\(i\)=1,...,n) is dissipation coordinate introduced by viscoelasticity. And

$$\begin{aligned} \gamma =\frac{\pi \left( {r_1 +r_2 } \right) l_1 }{r_2 -r_1 } \end{aligned}$$
(20)

depends on the size of the damper shown in Fig. 11.

Obviously, the matrices in Eq. (19) have the similar form as in Eq. (10), so the viscoleastic damper can also be seen as a vibration absorber. But the parameters of this absorber, \(\alpha ,\omega _{v},\xi _{v}\), depend on the viscoelastic material and cannot be changed. So the viscoelastic damper cannot be tuned to get the optimal performance as resonant shunt damper.

To compare the control effect of resonant damper and viscoelastic damper, three viscoleastic dampers are located in the same location as the piezoelectric transducers in Fig. 6. Using parameters in [16]: \(G^{\infty }=5\times 10^{6}\, {Pa}, \alpha =1, \omega _{v}=1000\, {rad}/ {s}, \xi _{v}=4\), the eigenvalues of the Kagome structure with dampers can be calculated. The first three mechanical modes and eigenvalues introduced by viscoelasticity are listed in Table 5. It can be seen that while the mechanical frequencies are decreased due to the low-stiffness of the dampers, there is hardly any damping is added to the mechanical modes because the modes introduced by the dissipation coordinates are overdamped. So, in general, because its parameters cannot be tuned, the viscoleastic damping cannot achieve the good damping-adding performance as resonant shunt damper.

Table 5 The first three mechanical modes and overdamped real eigenvalues introduced by viscoelasticity
Full size table

6 Conclusions

This work proposed an independent modal resonant shunt damping method for multimode vibration control and applied to a truss-cored sandwich panel using piezoelectric transducer. This method is general in the sense that it can also be used in other structures. In this method, modal transducers and modal shunts of different modes are kept well independent while significant damping is added to the controlled modes. These merits are validated by eigenvalue analysis and numerical simulation. It is also found that the optimal values of the resistance and the inductance can not be determined using low-order truncated model of the structure when the number of mechanical degree of freedoms are large. A practical optimization method is proposed, based on the independence between different modal shunts, that can reduce the \(2n\)-dimensional optimization problem to \(2n\) one-dimensional problems. Finally, the traditional viscoelastic damper is compared with the resonant shunt damper. It is pointed out that both the resonant shunt damper and the viscoelastic damper can be seen as a vibration absorber. But the resonant shunt can achieve better performance through tuning its parameters.