Synergistic damage mechanics development to predict elastoplastic behavior of an Al/GE laminate with transverse-cracks and plasticity damages

Abstract

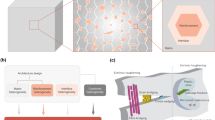
Synergistic damage mechanics (SDM) is a multiscale approach to predict the transverse-cracks effect on the composite laminates engineering moduli. Decreasing experiments needed for calibrating the model, the SDM considerably reduces the design cost. Despite the advantages, the method has not been applied to fiber-metal laminates (FML). While the FMLs undergo plasticity damage because of the metal layers, the SDM has been only developed for fibrous, polymeric composites that do not have plastic behavior; As such, the approach needs to be developed to consider the plasticity before implementation in FMLs. In this paper, SDM is developed to predict the stiffness degradation and elastoplastic behavior of the FMLs with transverse-cracks and plasticity damages. Subsequently, three independent models based on the developed approach are proposed to case study an aluminum/glass/epoxy FML. Then, each model is separately analyzed mathematically, and the equations of engineering moduli are derived. The models are calibrated using a finite-element (FE) micromechanical model of a reference laminate. Then, the SDM models are validated with a recently introduced modified in situ digital microscopy accompanied by the quasi-static loading–unloading test and the FE micromechanical model of the FML. Relating the unknown plastic behavior of the FML to the known plastic behavior of its metal layers, the best SDM model is further developed to predict the stress–strain diagram of the FML and validated with the tension tests.

Appendix A

The following Appendix presents derived equations from the theoretical analysis of the proposed polynomial functions. The procedure to derive these equations is almost the same as described in Sect. 6.1. So, only the derived equations are presented.

1.1 A.1: The second-order model formulae

For the proposed second-order Helmholtz function of Eq. (32), the following equations are derived to predict the engineering moduli:

$${E}_{x}={\omega }_{m}\left(1-{D}_{m}\right)\frac{{E}_{m}^{0}}{1-{\nu }_{m}^{2}}+{\omega }_{nm}\left(\frac{{E}_{xnm}^{0}}{1-{\nu }_{xynm}^{0}{\nu }_{yxnm}^{0}}+2\frac{{\kappa }_{nm}{t}_{c}^{2}}{s{t}_{nm}}{a}_{1nm}+2\frac{{\kappa }_{nm}^{2}{t}_{c}^{4}}{{s}^{2}{t}_{nm}^{2}}{b}_{1nm}\right)-{\left({\omega }_{m}\left(1-{D}_{m}\right)\frac{{\nu }_{m}{E}_{m}^{0}}{1-{\nu }_{m}^{2}}+{\omega }_{nm}\left(\frac{{{\nu }_{xynm}^{0}E}_{ynm}^{0}}{1-{\nu }_{xynm}^{0}{\nu }_{yxnm}^{0}}+\frac{{\kappa }_{nm}{t}_{c}^{2}}{s{t}_{nm}}{a}_{4nm}+\frac{{\kappa }_{nm}^{2}{t}_{c}^{4}}{{s}^{2}{t}_{nm}^{2}}{b}_{4nm}\right)\right)}^{2}/\left({\omega }_{m}\left(1-{D}_{m}\right)\frac{{E}_{m}^{0}}{1-{\nu }_{m}^{2}}+{\omega }_{nm}\left(\frac{{E}_{ynm}^{0}}{1-{\nu }_{xynm}^{0}{\nu }_{yxnm}^{0}}+2\frac{{\kappa }_{nm}{t}_{c}^{2}}{s{t}_{nm}}{a}_{2nm}+2\frac{{\kappa }_{nm}^{2}{t}_{c}^{4}}{{s}^{2}{t}_{nm}^{2}}{b}_{2nm}\right)\right)$$

(37)

$${E}_{y}={\omega }_{m}\left(1-{D}_{m}\right)\frac{{E}_{m}^{0}}{1-{\nu }_{m}^{2}}+{\omega }_{nm}\left(\frac{{E}_{ynm}^{0}}{1-{\nu }_{xynm}^{0}{\nu }_{yxnm}^{0}}+2\frac{{\kappa }_{nm}{t}_{c}^{2}}{s{t}_{nm}}{a}_{2nm}+2\frac{{\kappa }_{nm}^{2}{t}_{c}^{4}}{{s}^{2}{t}_{nm}^{2}}{b}_{2nm}\right)-{\left({\omega }_{m}\left(1-{D}_{m}\right)\frac{{\nu }_{m}{E}_{m}^{0}}{1-{\nu }_{m}^{2}}+{\omega }_{nm}\left(\frac{{{\nu }_{xynm}^{0}E}_{ynm}^{0}}{1-{\nu }_{xynm}^{0}{\nu }_{yxnm}^{0}}+\frac{{\kappa }_{nm}{t}_{c}^{2}}{s{t}_{nm}}{a}_{4nm}+\frac{{\kappa }_{nm}^{2}{t}_{c}^{4}}{{s}^{2}{t}_{nm}^{2}}{b}_{4nm}\right)\right)}^{2}/ \left({\omega }_{m}\left(1-{D}_{m}\right)\frac{{E}_{m}^{0}}{1-{\nu }_{m}^{2}}+{\omega }_{nm}\left(\frac{{E}_{xnm}^{0}}{1-{\nu }_{xynm}^{0}{\nu }_{yxnm}^{0}}+2\frac{{\kappa }_{nm}{t}_{c}^{2}}{s{t}_{nm}}{a}_{1nm}+2\frac{{\kappa }_{nm}^{2}{t}_{c}^{4}}{{s}^{2}{t}_{nm}^{2}}{b}_{1nm}\right)\right)$$

(38)

$${\nu }_{xy}=\left({\omega }_{m}\left(1-{D}_{m}\right)\frac{{\nu }_{m}{E}_{m}^{0}}{1-{\nu }_{m}^{2}}+{\omega }_{nm}\left(\frac{{{\nu }_{xynm}^{0}E}_{ynm}^{0}}{1-{\nu }_{xynm}^{0}{\nu }_{yxnm}^{0}}+\frac{{\kappa }_{nm}{t}_{c}^{2}}{s{t}_{nm}}{a}_{4nm} +\frac{{\kappa }_{nm}^{2}{t}_{c}^{4}}{{s}^{2}{t}_{nm}^{2}}{b}_{4nm}\right)\right)/\left({\omega }_{m}\left(1-{D}_{m}\right)\frac{{E}_{m}^{0}}{1-{\nu }_{m}^{2}}+{\omega }_{nm}\left(\frac{{E}_{ynm}^{0}}{1-{\nu }_{xynm}^{0}{\nu }_{yxnm}^{0}}+2\frac{{\kappa }_{nm}{t}_{c}^{2}}{s{t}_{nm}}{a}_{2nm}+2\frac{{\kappa }_{nm}^{2}{t}_{c}^{4}}{{s}^{2}{t}_{nm}^{2}}{b}_{2nm}\right)\right)$$

(39)

$${G}_{xy}={\omega }_{m}\left(1-{D}_{m}\right)\frac{{E}_{m}^{0}}{\left(1+{\nu }_{m}\right)}+{\omega }_{nm}\left({G}_{xynm}^{0}+2\frac{{\kappa }_{nm}{t}_{c}^{2}}{s{t}_{nm}}{a}_{3nm}+2\frac{{\kappa }_{nm}^{2}{t}_{c}^{4}}{{s}^{2}{t}_{nm}^{2}}{b}_{3nm}\right)$$

(40)

where ${\kappa }_{nm}{a}_{inm}$ and ${{\kappa }_{nm}^{2}b}_{inm}$ are eight damage constants that need to be obtained. The following equations are needed for this goal:

$$\frac{{E}_{xnm}}{1-{\nu }_{xynm}{\nu }_{yxnm}}=\frac{{E}_{xnm}^{0}}{1-{\nu }_{xynm}^{0}{\nu }_{yxnm}^{0}}+\frac{2{t}_{c}^{2}}{s{t}_{nm}}{\kappa }_{nm}{a}_{1nm}+\frac{2{t}_{c}^{4}}{{s}^{2}{t}_{nm}^{2}}{{\kappa }_{nm}^{2}b}_{1nm}$$

(41)

$$\frac{{E}_{ynm}}{1-{\nu }_{xynm}{\nu }_{yxnm}}=\frac{{E}_{ynm}^{0}}{1-{\nu }_{xynm}^{0}{\nu }_{yxnm}^{0}}+\frac{2{t}_{c}^{2}}{s{t}_{nm}}{\kappa }_{nm}{a}_{2nm}+\frac{2{t}_{c}^{4}}{{s}^{2}{t}_{nm}^{2}}{{\kappa }_{nm}^{2}b}_{2nm}$$

(42)

$$\frac{{\nu }_{xynm}{E}_{ynm}}{1-{\nu }_{xynm}{\nu }_{yxnm}}=\frac{{{\nu }_{xynm}^{0}E}_{ynm}^{0}}{1-{\nu }_{xynm}^{0}{\nu }_{yxnm}^{0}}+\frac{{t}_{c}^{2}}{s{t}_{nm}}{{\kappa }_{nm}a}_{4nm}+\frac{{t}_{c}^{4}}{{s}^{2}{t}_{nm}^{2}}{{\kappa }_{nm}^{2}b}_{4nm}$$

(43)

$${G}_{xynm}={G}_{xynm}^{0}+\frac{2{t}_{c}^{2}}{s{t}_{nm}}{\kappa }_{nm}{a}_{3nm}+\frac{2{t}_{c}^{4}}{{s}^{2}{t}_{nm}^{2}}{{\kappa }_{nm}^{2}b}_{3nm}$$

(44)

In the case of the second-order function, two reference states of cross-ply glass/epoxy damage are needed. Taking the parameters ${\kappa }_{nm}{a}_{inm}$ and ${{\kappa }_{nm}^{2}b}_{inm}$ as the unknowns ${x}_{i}$ and ${y}_{i}$ for simplicity, Eqs. (41–44) are a general form of Eq. (45):

$${q}_{1i}\left(s\right)={q}_{2i}+{q}_{3i}\left(s\right){x}_{i}+{q}_{4i}\left(s\right){y}_{i}$$

(45)

Substituting two reference states of $s={s}_{1}$ and $s={s}_{2}$, a system of eight linear equations is generated:

$$\begin{aligned} q_{11} \left( {s_{1} } \right) & = q_{21} + q_{31} \left( {s_{1} } \right)x_{1} + q_{41} \left( {s_{1} } \right)y_{1} \\ q_{11} \left( {s_{2} } \right) & = q_{21} + q_{31} \left( {s_{2} } \right)x_{1} + q_{41} \left( {s_{2} } \right)y_{1} \\ q_{12} \left( {s_{1} } \right) & = q_{22} + q_{32} \left( {s_{1} } \right)x_{2} + q_{42} \left( {s_{1} } \right)y_{2} \\ q_{12} \left( {s_{2} } \right) & = q_{22} + q_{32} \left( {s_{2} } \right)x_{2} + q_{42} \left( {s_{2} } \right)y_{2} \\ q_{13} \left( {s_{1} } \right) & = q_{23} + q_{33} \left( {s_{1} } \right)x_{3} + q_{43} \left( {s_{1} } \right)y_{3} \\ q_{13} \left( {s_{2} } \right) & = q_{23} + q_{33} \left( {s_{2} } \right)x_{3} + q_{43} \left( {s_{2} } \right)y_{3} \\ q_{14} \left( {s_{1} } \right) & = q_{24} + q_{34} \left( {s_{1} } \right)x_{4} + q_{44} \left( {s_{1} } \right)y_{4} \\ q_{14} \left( {s_{2} } \right) & = q_{24} + q_{34} \left( {s_{2} } \right)x_{4} + q_{44} \left( {s_{2} } \right)y_{4} \\ \end{aligned}$$

(46)

which can be simplified in a matrix form:

$${Q}_{1}X={Q}_{2}$$

(47)

where:

$${Q}_{1}=\left[\begin{array}{cccccccc}{q}_{31}\left({s}_{1}\right)& {q}_{41}\left({s}_{1}\right)& 0& 0& 0& 0& 0& 0\\ {q}_{31}\left({s}_{2}\right)& {q}_{41}\left({s}_{2}\right)& 0& 0& 0& 0& 0& 0\\ 0& 0& {q}_{32}\left({s}_{1}\right)& {q}_{42}\left({s}_{1}\right)& 0& 0& 0& 0\\ 0& 0& {q}_{32}\left({s}_{2}\right)& {q}_{42}\left({s}_{2}\right)& 0& 0& 0& 0\\ 0& 0& 0& 0& {q}_{33}\left({s}_{1}\right)& {q}_{43}\left({s}_{1}\right)& 0& 0\\ 0& 0& 0& 0& {q}_{33}\left({s}_{2}\right)& {q}_{43}\left({s}_{2}\right)& 0& 0\\ 0& 0& 0& 0& 0& 0& {q}_{34}\left({s}_{1}\right)& {q}_{44}\left({s}_{1}\right)\\ 0& 0& 0& 0& 0& 0& {q}_{34}\left({s}_{2}\right)& {q}_{44}\left({s}_{2}\right)\end{array}\right]$$

(48)

$$X = \left[ {\begin{array}{*{20}c} {x_{1} } \\ {y_{1} } \\ {x_{2} } \\ {y_{2} } \\ {x_{3} } \\ {y_{3} } \\ {x_{4} } \\ {y_{4} } \\ \end{array} } \right],Q_{2} = \left[ {\begin{array}{*{20}c} {q_{11} \left( {s_{1} } \right) - q_{21} } \\ {q_{11} \left( {s_{2} } \right) - q_{21} } \\ {q_{12} \left( {s_{1} } \right) - q_{22} } \\ {q_{12} \left( {s_{2} } \right) - q_{22} } \\ {q_{13} \left( {s_{1} } \right) - q_{23} } \\ {q_{13} \left( {s_{2} } \right) - q_{23} } \\ {q_{14} \left( {s_{1} } \right) - q_{24} } \\ {q_{14} \left( {s_{2} } \right) - q_{24} } \\ \end{array} } \right]$$

(49)

The solution to the system of equations is as follows:

$$X={Q}_{1}^{-1}{Q}_{2}$$

(50)

1.2 A.2: The third-order model formulae

The appropriate derived equations of engineering moduli from the proposed third-order Helmholtz function of Eq. (33) are as follows:

$${E}_{x}={\omega }_{m}\left(1-{D}_{m}\right)\frac{{E}_{m}^{0}}{1-{\nu }_{m}^{2}}+{\omega }_{nm}\left(\frac{{E}_{xnm}^{0}}{1-{\nu }_{xynm}^{0}{\nu }_{yxnm}^{0}}+2\frac{{\kappa }_{nm}{t}_{c}^{2}}{s{t}_{nm}}{a}_{1nm}+2\frac{{\kappa }_{nm}^{2}{t}_{c}^{4}}{{s}^{2}{t}_{nm}^{2}}{b}_{1nm}+2\frac{{\kappa }_{nm}^{3}{t}_{c}^{6}}{{s}^{3}{t}_{nm}^{3}}{f}_{1nm}\right)-{\left({\omega }_{m}\left(1-{D}_{m}\right)\frac{{\nu }_{m}{E}_{m}^{0}}{1-{\nu }_{m}^{2}}+{\omega }_{nm}\left(\frac{{{\nu }_{xynm}^{0}E}_{ynm}^{0}}{1-{\nu }_{xynm}^{0}{\nu }_{yxnm}^{0}}+\frac{{\kappa }_{nm}{t}_{c}^{2}}{s{t}_{nm}}{a}_{4nm}+\frac{{\kappa }_{nm}^{2}{t}_{c}^{4}}{{s}^{2}{t}_{nm}^{2}}{b}_{4nm}+\frac{{\kappa }_{nm}^{3}{t}_{c}^{6}}{{s}^{3}{t}_{nm}^{3}}{f}_{4nm}\right)\right)}^{2}/\left({\omega }_{m}\left(1-{D}_{m}\right)\frac{{E}_{m}^{0}}{1-{\nu }_{m}^{2}}+{\omega }_{nm}\left(\frac{{E}_{ynm}^{0}}{1-{\nu }_{xynm}^{0}{\nu }_{yxnm}^{0}}+2\frac{{\kappa }_{nm}{t}_{c}^{2}}{s{t}_{nm}}{a}_{2nm}+2\frac{{\kappa }_{nm}^{2}{t}_{c}^{4}}{{s}^{2}{t}_{nm}^{2}}{b}_{2nm}+2\frac{{\kappa }_{nm}^{3}{t}_{c}^{6}}{{s}^{3}{t}_{nm}^{3}}{f}_{2nm}\right)\right)$$

(51)

$${E}_{y}= {\omega }_{m}\left(1-{D}_{m}\right)\frac{{E}_{m}^{0}}{1-{\nu }_{m}^{2}}+{\omega }_{nm}\left(\frac{{E}_{ynm}^{0}}{1-{\nu }_{xynm}^{0}{\nu }_{yxnm}^{0}}+2\frac{{\kappa }_{nm}{t}_{c}^{2}}{s{t}_{nm}}{a}_{2nm}+2\frac{{\kappa }_{nm}^{2}{t}_{c}^{4}}{{s}^{2}{t}_{nm}^{2}}{b}_{2nm}+2\frac{{\kappa }_{nm}^{3}{t}_{c}^{6}}{{s}^{3}{t}_{nm}^{3}}{f}_{2nm}\right)-{\left({\omega }_{m}\left(1-{D}_{m}\right)\frac{{\nu }_{m}{E}_{m}^{0}}{1-{\nu }_{m}^{2}}+{\omega }_{nm}\left(\frac{{{\nu }_{xynm}^{0}E}_{ynm}^{0}}{1-{\nu }_{xynm}^{0}{\nu }_{yxnm}^{0}}+\frac{{\kappa }_{nm}{t}_{c}^{2}}{s{t}_{nm}}{a}_{4nm}+\frac{{\kappa }_{nm}^{2}{t}_{c}^{4}}{{s}^{2}{t}_{nm}^{2}}{b}_{4nm}+\frac{{\kappa }_{nm}^{3}{t}_{c}^{6}}{{s}^{3}{t}_{nm}^{3}}{f}_{4nm}\right)\right)}^{2}/ \left({\omega }_{m}\left(1-{D}_{m}\right)\frac{{E}_{m}^{0}}{1-{\nu }_{m}^{2}}+{\omega }_{nm}\left(\frac{{E}_{xnm}^{0}}{1-{\nu }_{xynm}^{0}{\nu }_{yxnm}^{0}}+2\frac{{\kappa }_{nm}{t}_{c}^{2}}{s{t}_{nm}}{a}_{1nm}+2\frac{{\kappa }_{nm}^{2}{t}_{c}^{4}}{{s}^{2}{t}_{nm}^{2}}{b}_{1nm}+2\frac{{\kappa }_{nm}^{3}{t}_{c}^{6}}{{s}^{3}{t}_{nm}^{3}}{f}_{1nm}\right)\right)$$

(52)

$${\nu }_{xy}=\left({\omega }_{m}\left(1-{D}_{m}\right)\frac{{\nu }_{m}{E}_{m}^{0}}{1-{\nu }_{m}^{2}}+{\omega }_{nm}\left(\frac{{{\nu }_{xynm}^{0}E}_{ynm}^{0}}{1-{\nu }_{xynm}^{0}{\nu }_{yxnm}^{0}}+\frac{{\kappa }_{nm}{t}_{c}^{2}}{s{t}_{nm}}{a}_{4nm} +\frac{{\kappa }_{nm}^{2}{t}_{c}^{4}}{{s}^{2}{t}_{nm}^{2}}{b}_{4nm}+\frac{{\kappa }_{nm}^{3}{t}_{c}^{6}}{{s}^{3}{t}_{nm}^{3}}{f}_{4nm}\right)\right)/\left({\omega }_{m}\left(1-{D}_{m}\right)\frac{{E}_{m}^{0}}{1-{\nu }_{m}^{2}}+{\omega }_{nm}\left(\frac{{E}_{ynm}^{0}}{1-{\nu }_{xynm}^{0}{\nu }_{yxnm}^{0}}+2\frac{{\kappa }_{nm}{t}_{c}^{2}}{s{t}_{nm}}{a}_{2nm}+2\frac{{\kappa }_{nm}^{2}{t}_{c}^{4}}{{s}^{2}{t}_{nm}^{2}}{b}_{2nm}+2\frac{{\kappa }_{nm}^{3}{t}_{c}^{6}}{{s}^{3}{t}_{nm}^{3}}{f}_{2nm}\right)\right)$$

(53)

$${G}_{xy}={\omega }_{m}\left(1-{D}_{m}\right)\frac{{E}_{m}^{0}}{\left(1+{\nu }_{m}\right)}+{\omega }_{nm}\left({G}_{xynm}^{0}+2\frac{{\kappa }_{nm}{t}_{c}^{2}}{s{t}_{nm}}{a}_{3nm}+2\frac{{\kappa }_{nm}^{2}{t}_{c}^{4}}{{s}^{2}{t}_{nm}^{2}}{b}_{3nm}+2\frac{{\kappa }_{nm}^{3}{t}_{c}^{6}}{{s}^{3}{t}_{nm}^{3}}{f}_{3nm}\right)$$

(54)

where ${\kappa }_{nm}{a}_{inm}$, ${{\kappa }_{nm}^{2}b}_{inm}$, and ${{\kappa }_{nm}^{3}f}_{inm}$ are 12 damage constants that need to be obtained using three reference states of damage for the glass/epoxy laminate and the following equations:

$$\frac{{E}_{xnm}}{1-{\nu }_{xynm}{\nu }_{yxnm}}=\frac{{E}_{xnm}^{0}}{1-{\nu }_{xynm}^{0}{\nu }_{yxnm}^{0}}+\frac{2{t}_{c}^{2}}{s{t}_{nm}}{\kappa }_{nm}{a}_{1nm}+\frac{2{t}_{c}^{4}}{{s}^{2}{t}_{nm}^{2}}{{\kappa }_{nm}^{2}b}_{1nm}+\frac{2{t}_{c}^{6}}{{s}^{3}{t}_{nm}^{3}}{\kappa }_{nm}^{3}{f}_{1nm}$$

(55)

$$\frac{{E}_{ynm}}{1-{\nu }_{xynm}{\nu }_{yxnm}}=\frac{{E}_{ynm}^{0}}{1-{\nu }_{xynm}^{0}{\nu }_{yxnm}^{0}}+\frac{2{t}_{c}^{2}}{s{t}_{nm}}{\kappa }_{nm}{a}_{2nm}+\frac{2{t}_{c}^{4}}{{s}^{2}{t}_{nm}^{2}}{{\kappa }_{nm}^{2}b}_{2nm}+\frac{2{t}_{c}^{6}}{{s}^{3}{t}_{nm}^{3}}{{\kappa }_{nm}^{3}f}_{2nm}$$

(56)

$$\frac{{\nu }_{xynm}{E}_{ynm}}{1-{\nu }_{xynm}{\nu }_{yxnm}}=\frac{{{\nu }_{xynm}^{0}E}_{ynm}^{0}}{1-{\nu }_{xynm}^{0}{\nu }_{yxnm}^{0}}+\frac{{t}_{c}^{2}}{s{t}_{nm}}{{\kappa }_{nm}a}_{4nm}+\frac{{t}_{c}^{4}}{{s}^{2}{t}_{nm}^{2}}{{\kappa }_{nm}^{2}b}_{4nm}+\frac{{t}_{c}^{6}}{{s}^{3}{t}_{nm}^{3}}{\kappa }_{nm}^{3}{f}_{4nm}$$

(57)

$${G}_{xynm}={G}_{xynm}^{0}+\frac{2{t}_{c}^{2}}{s{t}_{nm}}{\kappa }_{nm}{a}_{3nm}+\frac{2{t}_{c}^{4}}{{s}^{2}{t}_{nm}^{2}}{{\kappa }_{nm}^{2}b}_{3nm}+\frac{2{t}_{c}^{6}}{{s}^{3}{t}_{nm}^{3}}{{\kappa }_{nm}^{3}f}_{3nm}$$

(58)

Equations (55–58) are a general form of Eq. (59):

$${q}_{1i}\left(s\right)={q}_{2i}+{q}_{3i}\left(s\right){x}_{i}+{q}_{4i}\left(s\right){y}_{i}+{q}_{5i}\left(s\right){z}_{i}$$

(59)

which is a system of 12 linear equations. The system can be solved through a similar procedure described in Sect. A.1 and Eqs. (46–50).