An enhanced approach for damage detection using the electromechanical impedance with temperature effects compensation

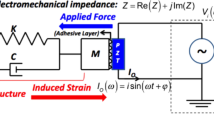
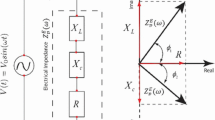
Abstract

Damage detection is one of the great challenges of the maintenance tasks and it has involved numerous researches to develop techniques in the field of structural health monitoring (SHM). Among different techniques, electromechanical impedance (EMI) technique has attracted attention due to its important and promising results. However, the sensitivity of this technique to variations in environmental conditions can lead to false diagnoses, and the temperature is one of the most critical factors for EMI technique. In view of this point, different researchers have developed compensation techniques to minimize the effects caused by temperature variation in electromechanical impedance measurements. Another important issue related to electromechanical Impedance curves is about the frequency range chosen to be analyzed. Then, the present article introduces an improved approach for damage detection by adding a new step for the temperature compensation technique proposed in a well-established approach in the literature. The proposal comprises a strategy to select the frequency range to compute damage detection indexes, and the technique is demonstrated for an aluminum beam in three different structural conditions: corresponding to the healthy and two types of damaged structure. The results are investigated for four different frequency ranges. The findings demonstrate the effectiveness of the proposed approach to reduce false alarms in damage detection using the EMI technique.

Appendices

Appendix 1 Overview on the Park et al. [26] compensation technique

This appendix shows the EMI curves when applying the Park et al. [26] temperature compensation technique. Figure 24 shows the real part of the EMI obtained for the aluminum beam in the undamaged condition in two different temperatures (10 and 30 $^{\circ }$C) and 4 different stages of the method (i.e., iterations). The values of $V_a$ and $\delta ^S$ for each iteration are shown in Table 4. After the first iteration the difference in the vertical axis reduced by summing $\delta ^S$ to the curve. This parameter presents a small variation even after multiple iterations, as shown in Table 4. This characteristics is verified because $\delta ^S$ is computed by the difference between $Z_R$ and the measured signal shifted horizontally.

Park et al. [26] verified that it is possible to detect damages in the incipient phases, even considering temperature variations from 25 to 75 $^{\circ }$C, with a step of 12.5 $^{\circ }$C. The experiments were carried out in different frequency ranges according to the monitored structure: carbon steel beam (70–80 kHz), bolted pipe joint (70–80 kHz), gears (190–220 kHz), and composite-reinforced structure (54–63 kHz).

Table 4 Values of $V_a$ and ${\delta ^{S}}$ in each iteration

Fig. 24

Real part of electromechanical impedance at different iterations of Park et al. [26] technique: 10 °C (black continuous line) and 30 °C (blue-dashed line)

Appendix 2 Results for the frequency ranges numbers 1 and 2 (Table 3)

Figures 25, 26 and 27 show the EMI signal after applying the approach proposed by Park et al. [26]. These figures contain, respectively, the signals for the undamaged condition, with damage 1 (added mass) and damage 2 (mechanical cut) for two different frequency ranges, corresponding to the bandwidths 15 and 30 kHz. The values of the difference between the RMSD and CCDM of the signals for both damaged and undamaged conditions are shown in Figs. 28 and 29. Figure 30 shows similar results regarding damage detection (i.e., no false negatives) for the frequency range number 2 (bandwidth 30 kHz) after applying the new approach. On the other hand, Appendix 3 shows that this approach can not be successfully applied by considering the frequency range number 1 because a stable value of S is not achieved.

Fig. 25

Real part of the electromechanical impedance (undamaged condition) using Park et al. [26] compensation technique for two frequency bandwidths: 15 and 30 kHz. Curves for the temperatures $-10\,^{\circ }$C, 4 $^{\circ }$C, 24 $^{\circ }$C (reference), 36 $^{\circ }$C, 52 $^{\circ }$C, 64 $^{\circ }$C and 80 $^{\circ }$C

Fig. 26

Real part of the electromechanical impedance (damage 1) using Park et al. [26] compensation technique for two frequency bandwidths: 15 and 30 kHz. Curves for the temperatures $-10\,^{\circ }$C, 5 $^{\circ }$C, 25 $^{\circ }$C, 35 $^{\circ }$C, 50 $^{\circ }$C, 65 $^{\circ }$C and 80 $^{\circ }$C

Fig. 27

Real part of the electromechanical impedance (damage 2) using Park et al. [26] compensation technique for two frequency bandwidths: 15 and 30 kHz. Curves for the temperatures $-10\,^{\circ }$C, 5 $^{\circ }$C, 25 $^{\circ }$C, 35 $^{\circ }$C, 50 $^{\circ }$C, 65 $^{\circ }$C and 80 $^{\circ }$C

Fig. 28

Difference between the RMSD values computed for the signals in the damaged and undamaged conditions compensated by Park et al. [26] technique for the FR numbers 1 and 2. Yellow slanted bar hatch depicts damage 1 and blue bar with horizontal hatch represents damage 2

Fig. 29

Difference between the CCDM values computed for the signals in the damaged and undamaged conditions compensated by Park et al. [26] technique for the FR numbers 1 and 2. Yellow slanted bar hatch depicts damage 1 and blue bar with horizontal hatch represents damage 2

Fig. 30

Difference between the RMSD and CCDM values computed for the signals in the damaged and undamaged conditions after applying the new approach for the FR number 2. Yellow slanted bar hatch depicts damage 1 and blue bar with horizontal hatch represents damage 2

Appendix 3 Analysis of the S-curve

Table 5 shows the values of S for each frequency range. Note that it is numerically approximately a constant value (around $10^3$) for the frequency ranges 2, 3 and 4. However, its variation is more significant for the frequency range number 1.

This behavior suggests that the approach can not be successfully applied when using this frequency range. Then, the evaluation of the parameter S is an important part of this proposed strategy to select the frequency range.

Table 5 S and $N_r$ values for the four frequency ranges (FR)